一種基于Bessel函數的混沌神經網絡
葉永剛,徐耀群
(哈爾濱商業大學基礎科學學院,哈爾濱150028)
A·Potapove等指出,如果混沌神經元的激勵函數是非單調函數,則單神經元能較快地執行混沌搜索[1].Shuai等提出有效的激勵函數可以是不同的表現形式,并且應該表現出混沌行為[2].目前已有多種類型的混沌神經網絡模型,并已用其成功地解決了組合優化問題[3-5],但多數的混沌神經網絡的神經元激勵函數采用單調遞增的函數[6-9].本文在Chen-Aihara暫態混沌神經網絡的基礎上提出了一種新的暫態混沌神經網絡模型,在此模型中我們選擇了具有較高的非線性度及較好的函數逼近能力的Bessel函數與Sigmoid函數的組合作為新的激勵函數,構建了一種新的混沌神經元模型,該激勵函數為非單調遞增但總體上是遞增的函數.利用混沌神經元的倒分叉圖和最大Lyapunov指數時間演化圖分析了新的暫態混沌神經網絡的動力學特性.利用這種新的暫態混沌神經元模型我們建立了一種暫態神經網絡,通過對所選擇的非線性函數優化和10個城市的TSP問題的求解驗證了此模型具有更快地找到全局最小的能力.
1 基于Bessel函數的混沌神經網絡模型
1.1 Bessel函數
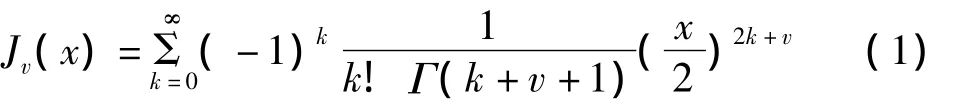
當v=-1,0,1時Bessel函數的圖像如圖1所示.
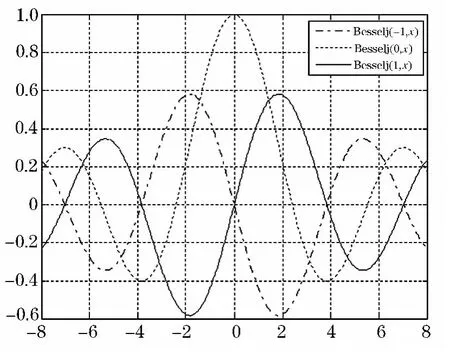
圖1 v=-1,0,1時圖像
由圖1知,當v=-1,1時Bessel函數是奇函數,當v=0時Bessel函數是偶函數,且Bessel函數當x→∞時是震蕩衰減的.
1.2 暫態混沌神經元模型
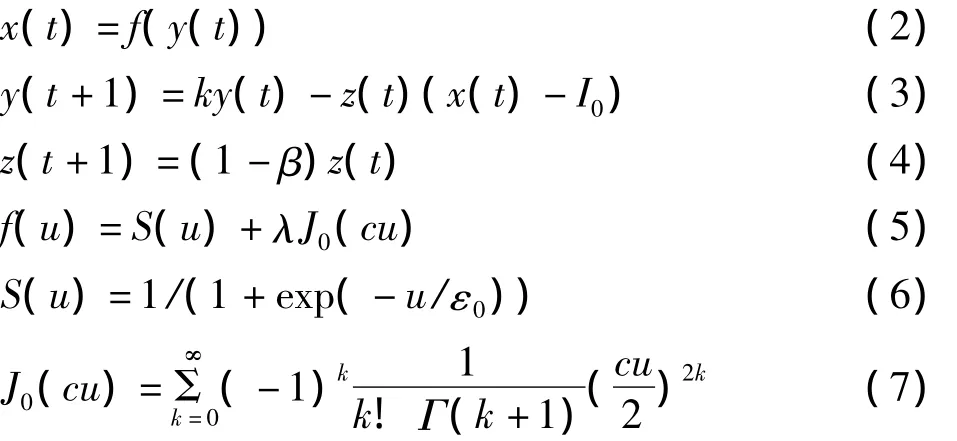
利用Bessel函數的特性,我們構造一種新暫態混沌的神經元模型,模型中激勵函數為0階的Bessel函數與Sigmoid函數的組合,取適當的參數后,激勵函數為非單調遞增但總體上是遞增的函數,稱此模型為Sigmoid-Bessel-Function模型,簡稱SBF模型.如下:其中:y(t)為神經元在t時刻的內部狀態;x(t)為激勵函數即神經元在的t時刻的輸出;f(u)為該模型中激勵函數;k的取值范圍為0≤k≤1,表示神經元保留內部狀態的能力;z(t)是自反饋連接項;I0為正參數;β是模擬退火參數;λ為組合系數;c為Bessel函數的伸縮系數;ε0是激勵函數的陡度參數;
對于激勵函數f(u),若取參數λ=1/5,c=5,ε0=0.5時其圖像如圖2所示.
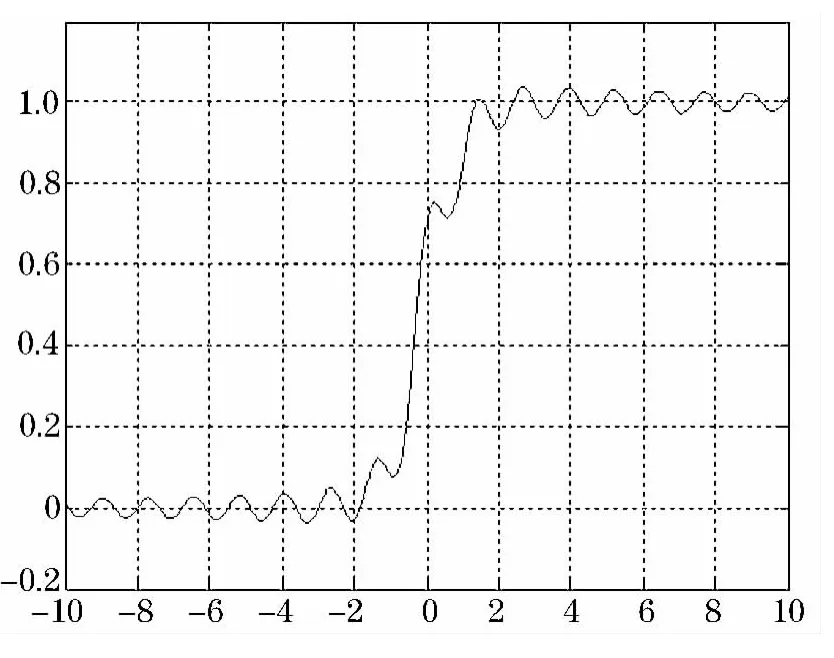
圖2 激勵函數在區間[-10,10]內的圖像
為進一步分析此暫態混沌神經元的混沌動力學特性,分別取參數y(1)=0.825,k=1,z(1)=0.85,ε0=0.04,I0=0.45,β=0.002,λ=1/5,c=5時得神經元的倒分岔圖和最大Lyapunov指數時間演化圖如圖3、4所示.
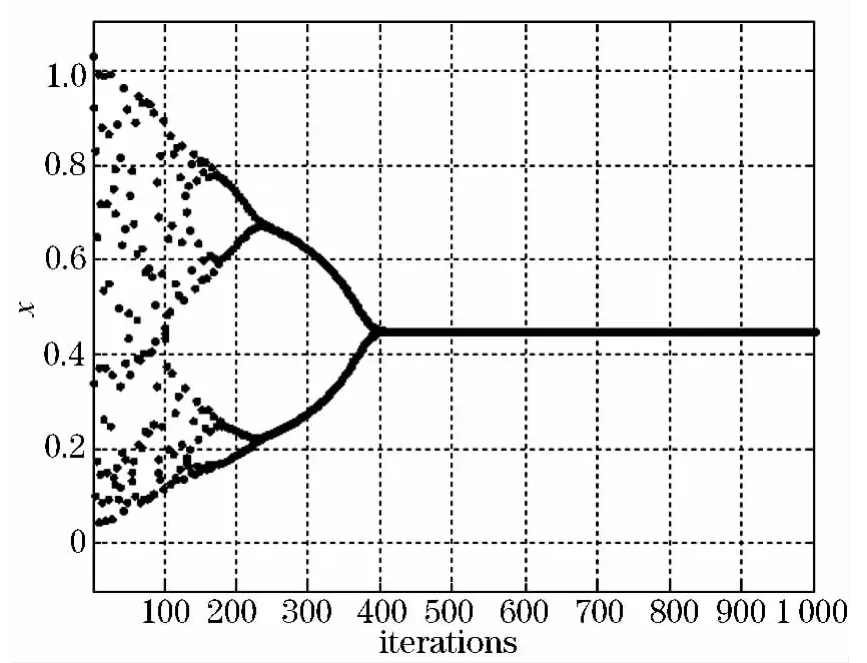
圖3 SBF模型的暫態混沌神經元倒分岔圖
由倒分岔圖3可知,SBF模型的神經元的輸出隨著的不斷衰減,經過一個混沌倒分岔過程逐漸穩定于平衡點.因此,網絡求解優化問題時,有利于克服一般隨機算法中以分布遍歷性為搜索機制帶來的局限性,使搜索具有內隨機性和軌道遍歷性,從而模型具有更強的避免收斂到局部極小的能力.
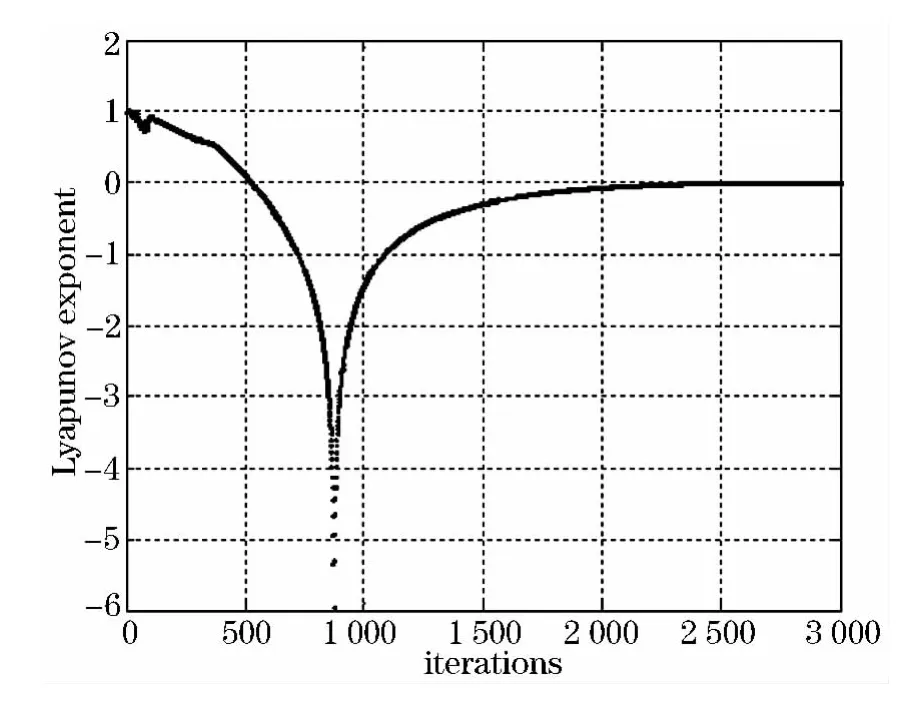
圖4 神經元最大Lyapunov指數時間演化圖
最大Lyapunov指數是經常用于定量描述混沌行為的量,當最大Lyapunov指數為正時,則神經元具有混沌動力學特性.由圖4可知,神經元在開始時最大Lyapunov指數為正,網絡處于混沌搜索狀態,但隨著自反饋連接項越來越小,最大Lyapunov指數由正逐漸變負,搜索逐漸失去混沌搜索能力,最終能使網絡處于一種穩定的平衡狀態.
綜上可知,該神經元模型具有暫態混沌動力學行為,由于混沌搜索具有內隨機性和軌道遍歷性,故此神經元模型能使網絡盡可能的避免收斂到局部最小值.
1.3 SBF暫態混沌神經網絡模型
1.3.1 Chen-Aihara暫態混沌神經網絡
Chen-Aihara神經網絡模型如下[10]:
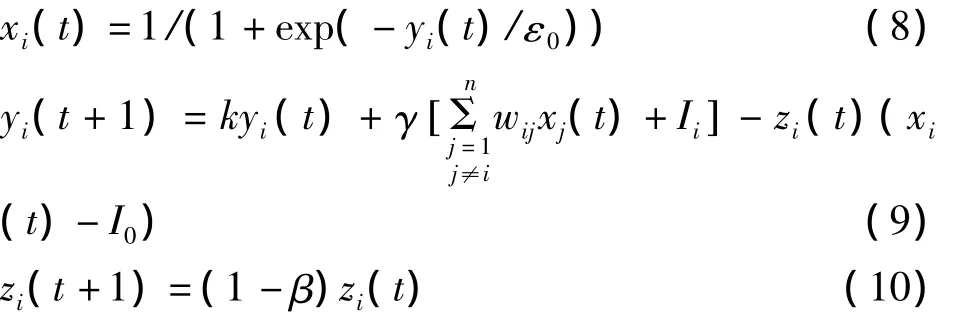
其中:xi(t)為激勵函數即第i個神經元在t時刻的輸出;其中yi(t)為第i個神經元在t時刻的內部狀態;ε0是激勵函數的陡度參數;k為神經隔膜的阻尼因子,0≤k≤1,代表網絡記憶保留或遺忘內部狀態的能力;γ為輸入的正的尺度參數,代表著能量函數對混沌動力學特性的影響;wij為神經元j與i的連接權值,且有wij=wji,wii=0;Ii為神經元i的輸入偏差;zi(t)為自反饋連接項,其值在模擬退火參數β的作用下不斷減小,最終使網絡處于一種穩定的平衡狀態;I0為一正參數.
1.3.2 SBF暫態混沌神經網絡
在Chen-Aihara神經網絡模型基礎上,利用構造的暫態混沌神經元模型,建立如下SBF暫態混沌神經網絡模型:
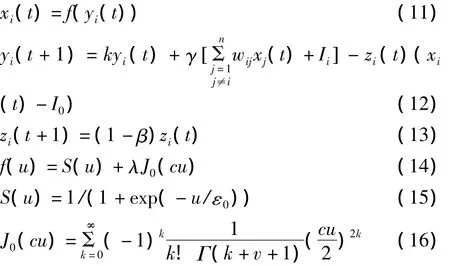
其中:xi(t)為激勵函數即第i個神經元在t時刻的輸出;其中yi(t)為第i個神經元在t時刻的內部狀態;ε0是激勵函數的陡度參數;k為神經隔膜的阻尼因子,0≤k≤1,代表網絡記憶保留或遺忘內部狀態的能力;γ為輸入的正的尺度參數,代表著能量函數對混沌動力學特性的影響;wij為神經元j與i的連接權值,且有wij=wji,wii=0;Ii為神經元i的輸入偏差;zi(t)為自反饋連接項,其值在模擬退火參數β的作用下不斷減小,最終使網絡處于一種穩定的平衡狀態;I0為一正參數;λ為組合系數;c為Bessel函數的伸縮系數.
2 SBF暫態混沌神經網絡模型在優化問題中的應用
2.1 SBF暫態混沌神經網絡模型在函數優化中的應用選取以下優化函數[11]:
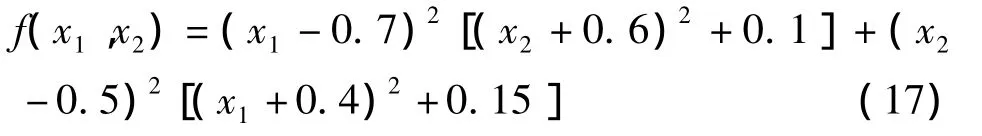
函數f的最小值為0,最小值點為(0.7,0.5);局部極小點為(0.6,0.4)與(0.6,0.5).
數據仿真中選取參數 ε0=0.4,k=1,γ=0.05,I0=0.45,β=0.002,y(1)=0.825,y(2)=0.825,z1(1)0.825,z1(1)=z2(1)=0.85時,SBF暫態混沌神經網絡模型求解優化函數f的能量函數演化如圖5所示.
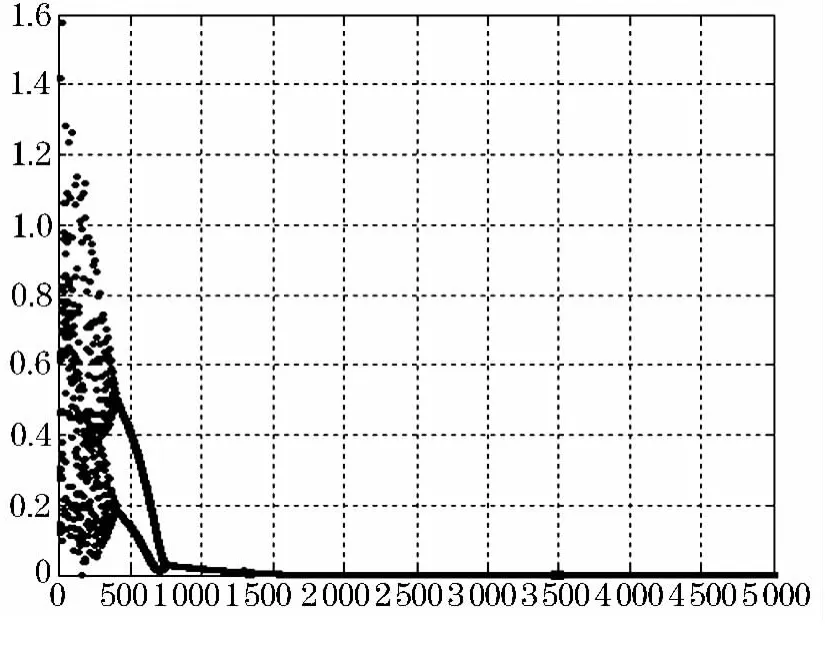
圖5 優化函數f的能量函數時間演化圖
兩個神經元輸出值x1,x2的時間演化如圖6所示.
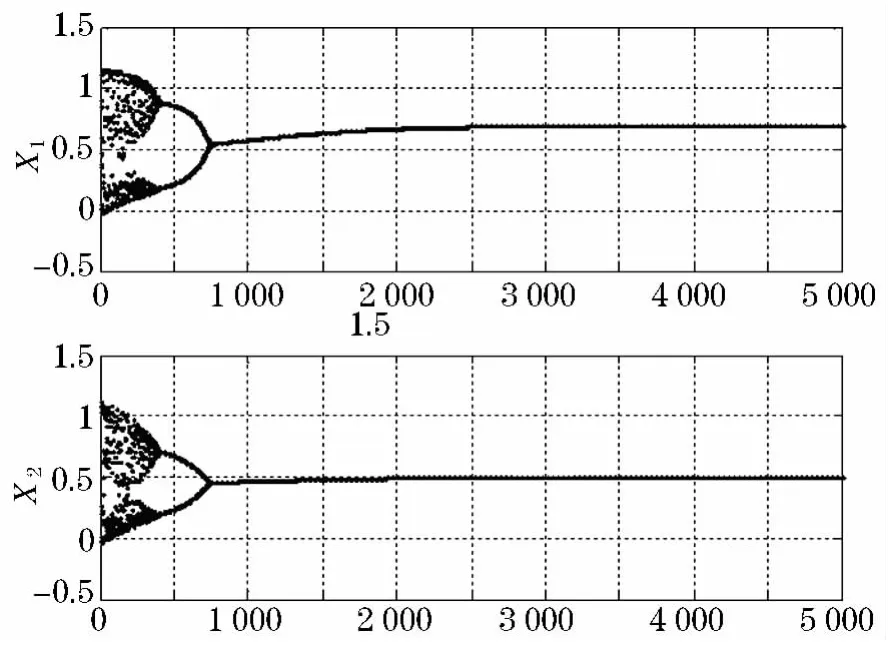
圖6 兩個神經元輸出值x1,x2時間演化圖
當網絡運行5 000次時優化函數的能量函數值為7.293 240 7×10-9,此時x1=0.699 928,x2=0.499 986,搜索逐漸收斂到最小值.
2.2 SBF暫態混沌神經網絡模型在TSP問題求解中的應用
TSP問題即旅行商最短路徑問題是一個最具代表性的組合優化問題,找到該問題一個行之有效的解法是多年來許多學者努力的目標.TSP問題可以簡述為:給定n個城市及任意兩城市之間的距離,要求確定一條經過所有城市且每個城市僅經過一次的最短路線.本文將SBF暫態混沌神經網絡模型應用于求解10個城市的TSP問題,仿真結果表明,此神經網絡模型比Chen-Aihara神經網絡模型具有更好的求解TSP問題的能力.
取能量函數為:
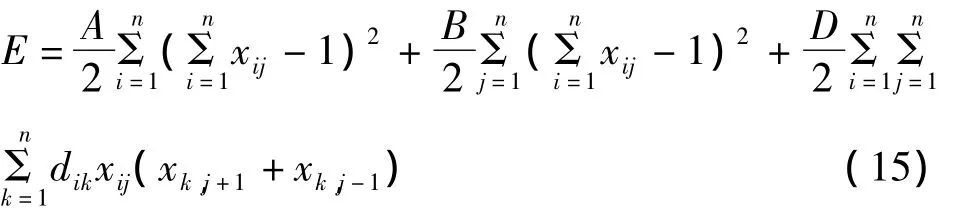
其中:dik為城市i到城市k的距離;xij表示以順序j訪問城市i,參數A=B,一個全局最小的能量值代表一條最短的有效路徑.
選取歸一化后的10個城市坐標,取值分別為:(0.4,0.443 9);(0.243 9,0.146 3);(0.170 7,0.229 3);(0.229 3,0.71 6);(0.517 1,0.941 4);(0.873 2,0.653 6);(0.687 8,0.521 9);(0.848 8,0.360 9);(0.668 3,0.253 6);(0.619 5,0.263 4)[5].該10個坐標的TSP問題滿足條件的最短路徑長度為2.677 6.
對于SBF暫態混沌神經網絡模型,選取參數A=B=1、D=2、γ=0.25、k=1、I0=0.4、ε0=0.5、z(1)=0.8、β=0.002,每次運行程序時,在區間(-0.1,01)內200次隨機賦予xij初值,程序共運行10次,其仿真結果如表1所示.
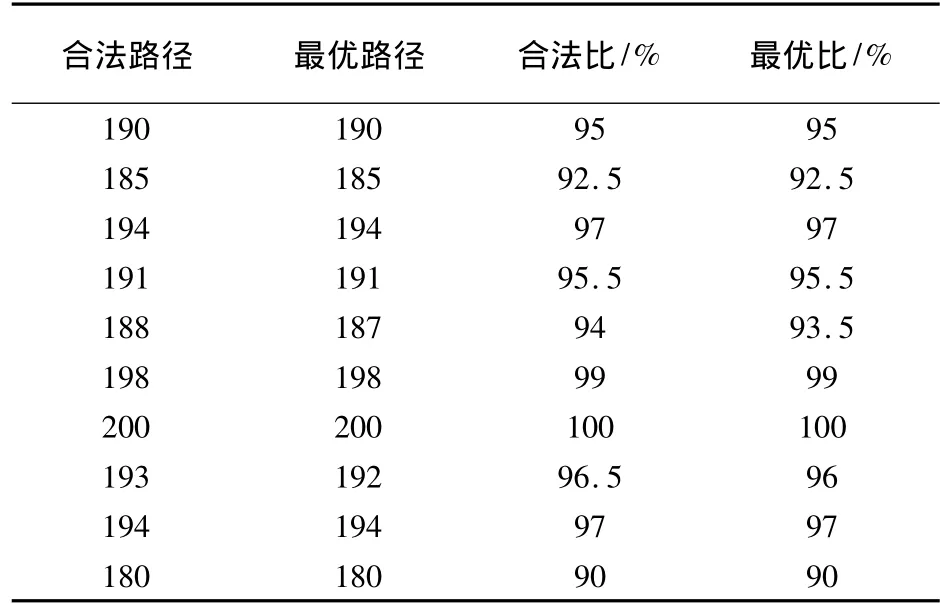
表1 SBF暫態混沌神經網絡求解10城市旅行商問題的運行結果
由表1知,該網絡求解10城市旅行商問題在上述參數情況下,其合法路徑比最大為100%,合法路徑比平均為95.7%,最優路徑比最大為100%,最優路徑比平均為95.6%,仿真結果表明,該神經網絡具有很好的解決TSP問題的能力.仿真得最優路徑如圖7所示.
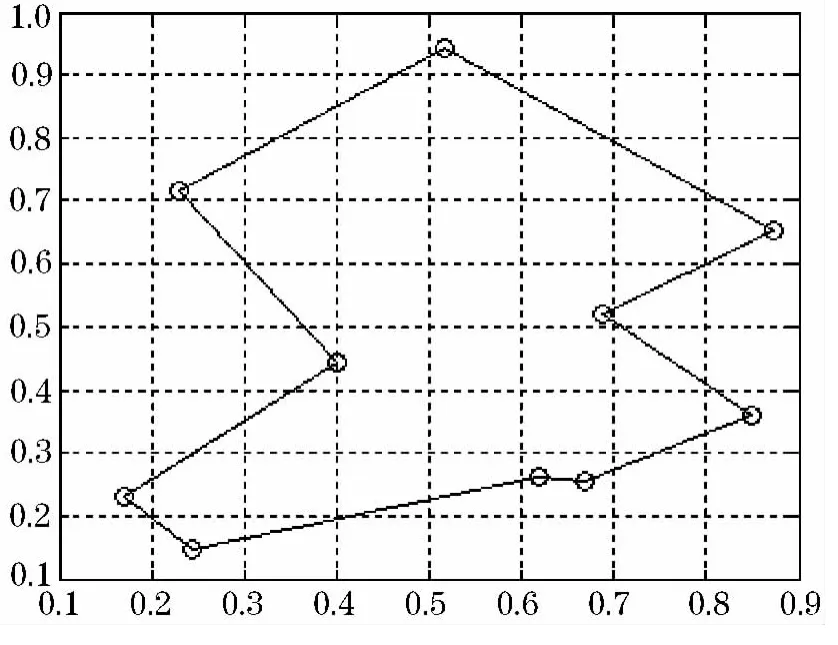
圖7 10城市TSP歸一化坐標的最短路徑
3 結語
由于Bessel函數具有很高的非線性度及較好的函數逼近能力,本文把0階Bessel函數引入到Chen-Aihara暫態混沌神經網絡中的激勵函數中,利用伸縮的0階Bessel函數和Sigmoid函數組合作為新的激勵函數,構建了一種新的暫態混沌神經網絡.將此模型應用到求解優化函數及TSP問題的最優解中,仿真結果表明,此模型具有很強的求最優解能力.本文的模型中激勵函數選取了固定的參數做了仿真實驗,對于激勵函數中參數的變化及高階Bessel函數對模型的影響是我們要進一步研究的內容.
[1]POTAPOVE A,KALIM.Robust chaos in neural networks[J].Physics Letters-A,2000,277(6):310-322.
[2]SHUAIJW,CHEN Z X,LIU R T,et al.Self-evolution neuralmodel[J].Physics Letters-A,1996,221(5):311-316.
[3]CHEN L,AIHARA K.Chaotic simulated annealing by a neural network modelwith transient chaos[J].Neural Networks,1995,8(6):915-930.
[4]徐耀群,楊學嶺,一類具有反三角函數自反饋的混沌神經網絡及其應用[J].哈爾濱商業大學學報:自然科學版,2010,26(3):324-328.
[5]徐耀群,孫 明.Shannon小波混沌神經網絡及其TSP(城市旅行商)問題的求解[J].控制理論與應用,2008,25(3):574-577.
[6]張 強,馬潤年,許 進.一種混沌神經網絡模型及其在優化中的應用[J].系統工程與電子技術,2002,24(2):48-50.
[7]修春波,劉向東.一種新的混沌神經網絡及其應用[J].電子學報,2005,33(5):868-870.
[8]XU Y Q,SUN M,SHEN JH.Shannon wavelet chaotic neural networks[J].Lecture Notes in Computer Science,2006,4247:244-251.
[9]賀昱曜,王力波.混沌神經網絡及其在最優化問題中的應用[J].控制理論與應用,2000,17(6):847-852.
[10]徐耀群,孫 明.混沌神經網絡及其應用[M].哈爾濱:黑龍江大學出版社,2012.
[11]王 濤,劉冬華.融合混沌和捕食搜索的混合粒子群算法[J].哈爾濱商業大學學報:自然科學版,2013,29(3):355-358.

