基于誤差修正的BP神經網絡含沙量預報模型

黃清烜，梁忠民，曹炎煦，霍世青，許珂艷

（1.河海大學 水文水資源學院，江蘇 南京 210098；2.黃河水利委員會 水文局，河南 鄭州 450004）

0 引言

黃河是世界上輸沙量最大、含沙量最高的河流之一。開展含沙量過程預報，不僅是黃河中下游干流水庫調度和洪水資源化的需要，也是下游變動河床水位預報的需要[1]。目前，含沙量預報的方法中，水文-水動力學方法主要包括輸沙單位線模型、響應函數模型、1-D～3D水沙數學模型等[2-7]。該類方法往往需要輸入大量的水文、氣象、河道特性、工程布局等資料且計算時間較長，因而限制了其應用范圍；基于宏觀因果關系的系統分析方法[8-11]，如神經網絡模型、支持向量機模型等對資料要求相對較低，在含沙量預報的實際應用中發揮著一定作用。

BP網絡模型在水文預報領域應用廣泛[12-14]。本文在借鑒已有BP網絡模型研究成果基礎上，建立了考慮上游來沙及區間降水的含沙量BP網絡預報模型，并將其應用于潼關站含沙量過程的預報；同時，結合誤差自回歸模型對BP網絡的預報結果進行校正，并對比分析了校正前后預報結果的精度，為實際應用提供參考。

1 BP網絡模型

BP（Back Propagation）網絡是一種按誤差逆傳播算法訓練的多層前饋網絡。標準的BP神經網絡收斂速度慢，易陷入局部最小點，對神經元個數比較敏感[12]。為此，眾多學者提出了各種改進方法[12-13]。動量-學習率自適應調整算法就是其中一種典型的改進方法。該方法可以有效地降低網絡對于誤差曲面局部細節的敏感性，提高收斂速度，并抑制網絡陷于局部極小值。其改進算法如下

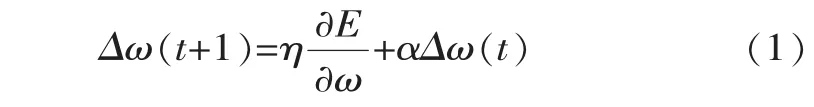
其中α為動量因子，0≤α＜1。學習率自適應調整法使學習率隨網絡訓練發生變化，在訓練開始階段學習率要取大些，有利于提高網絡的訓練速度；在訓練后期，學習率取小些，以保證網絡收斂在誤差最小點。該方法的實質就是在每個權重調整量上加上一項正比于前一項權重的值。

2 誤差自回歸實時校正模型

實時校正就是利用在作業預報過程中不斷得到的預報誤差信息，運用現代系統理論及時地校正、改善預報估計值或水文預報模型中的參數，盡可能地減小以后階段的預報誤差，使預報結果更接近實測值。根據與預報模型的結合方式，實時校正方法可分為預報與校正模型耦合及預報加校正模型兩類。其中，誤差自回歸實時校正模型簡單、實用。

誤差自回歸實時校正模型的工作原理:首先，采用確定性預報模型進行預報；之后，利用預報值與實測值之間隨時間變化的誤差序列建立誤差自回歸模型，預報未來誤差；最后，再將預報值與預報誤差值相加得出校正后的預報值。誤差自回歸估計的表達式可寫為

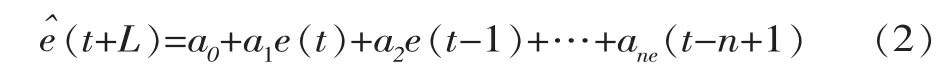
令k=0，1，2，…，n－1； 并考慮 ρk=ρ－k和ρ0=1， 可得到 n階線性方程組。即Yule-Walker方程

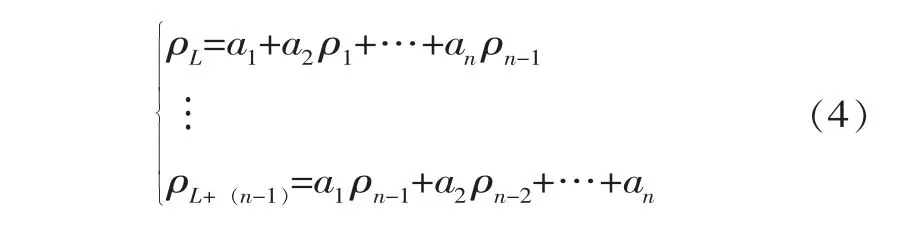
在實際應用中，通常采用樣本自相關函數r代替總體ρ來估計參數a，則式（3）可寫為[15]

其中，rk可以通過實際水文過程的離散點數據資料由

求得模型參數；a可用遞推公式求解，即由自回歸模型中已知的低階參數遞推求得高階參數。設a（i，j）表示i階自回歸模型中第j個參數，則遞推公式可寫為

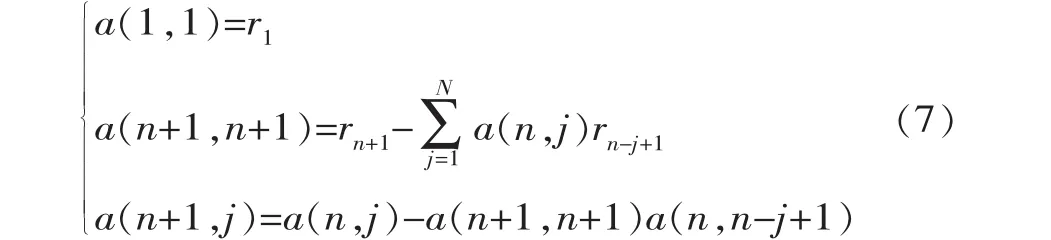
通過式（7）可求出自回歸系數 a1，a2，…，an， 進而求得 a0=u（1－（a1+a2+…+an））。 其中， u為誤差序列的期望，可以用樣本均值代替。

3 實例

3.1 流域基本資料

黃河中游龍門—潼關的河段干流河道長132.6 km，因其游蕩性的河道特性有別于晉陜峽谷河道（大北干流）而稱為小北干流，區間匯入的支流有汾河、涑水河、北洛河、渭河、涇河 （在高陵縣匯入渭河），其中渭河、汾河是黃河最大的兩條支流[16]。該河段為堆積性河段，河段比降上陡下緩，河床寬淺，水流散亂多邊，河心洲淺灘密布。該河段洪水多出現在汛期7月～10月，具有上漲快、歷時短、流量變幅大、含沙量高等特點。 “揭河底”是該段河流特殊的水文現象。

3.2 BP網絡預報模型的建立

潼關站的含沙量由其上游各支流的來沙及流域內降雨沖刷泥沙共同組成。按文獻[5]所提供的方法，選擇上游各控制站的含沙量Qsi（t－τi）和流域48 h的累積面平均雨量（t－υ）作為模型的輸入因子。其中，i為控制站的數目；τ為控制站到潼關的沙峰傳播時間；υ為累積面平均雨量對潼關站含沙量的影響滯時。在資料的收集過程中，發現北洛河和涑水河徑流量很小并經常出現斷流，直接導致狀頭站和張留莊站缺少含沙量的實測資料。為此，最終采用龍門、河津、華縣作為上游來沙的控制站。統計分析1980年～2005年的歷史洪水資料 （時段為1 h），確定龍門、河津、華縣到潼關的沙峰傳播時間τ分別為25、22、20 h，48 h累積面平均降雨量對潼關含沙量的影響滯時υ為20 h。分析最終確定， Qs龍（t－25）、Qs河（t－22）、Qs華（t－20）、（t－20）作為模型的輸入變量，Qs潼（t）作為模型的輸出變量。通過試算選取隱含層節點數為6，建立網絡拓撲為4-6-1，傳遞函數為Sigmoid函數的三層BP神經網絡模型。

在實際的網絡訓練過程中，考慮到以Sigmoid函數為傳遞函數的BP神經網絡的輸出值域均在[0，1]之間，并為消除因含沙量和降雨量量綱的不同對網絡識別精度的影響，需對輸入變量進行歸一化處理。本文用最大最小法進行數據的歸一化處理，計算公式如下:

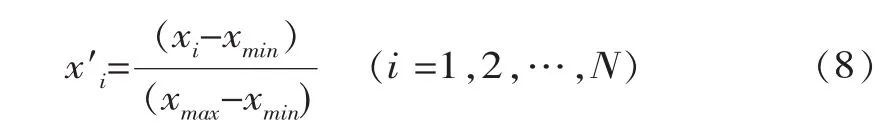
式中，xi、x′i分別為輸入變量歸一化前、后的輸入變量； xmin、xmax分別為輸入變量中的最小值和最大值；N表示訓練樣本的總個數。

3.3 實時校正模型的建立

通過樣本的訓練，確定BP網絡模型的權重及閾值，并基于該權重及閾值獲得潼關站的泥沙模擬結果。分析比較實測值與模擬值系列，求得誤差序列，并通過該誤差系列，建立誤差自回歸模型。設潼關站實測含沙量序列為｝，預報含沙量序列為｝，則誤差序列可表示為 e（i）=。 根據 AIC 準則法確定模型階數為5，建立預見期為6 h的誤差自回歸模型，表達式可寫為

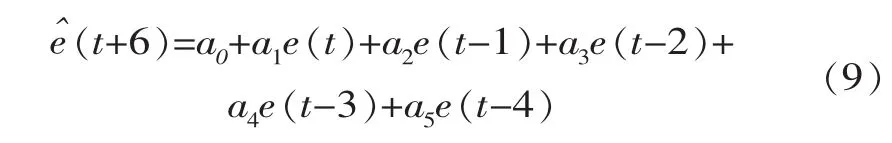
模型參數可以根據式（4）～式（7）進行求解。在校正的過程中，利用已有的誤差來預報未來6 h誤差，并對原來的預報結果進行修正；則，經過校正后的潼關站含沙量預報值為

3.4 含沙量過程預報誤差評定指標

由于含沙量變化的影響因素更為復雜，加之含沙量過程預報還處于探索階段，目前尚缺乏評價含沙量預報模型的合理標準[1]。為此，本文借鑒洪水過程預報中常用的精度評價指標，對含沙量過程預報精度進行評定[5]:①量值評定，包括沙峰、沙峰滯時、沙峰相對誤差；②過程評定，即比較含沙量預報過程線和實測含沙量過程線的擬合程度。本文采用確定性系數評定，計算公式為

式中，Sc為預報誤差值的均方差；σy為預報要素值的均方差；yi、y分別為實測含沙量、預報含沙量；為實測含沙量的均值。

3.5 模型檢驗

模型選取了潼關1980年～2005年間的12場泥沙過程作為訓練樣本。選取訓練次數為10000，學習速率為0.01，動量因子為0.9作為訓練參數對訓練樣本進行訓練。利用訓練樣本率定出的神經網絡各節點的權值與閾值對率定場次進行模擬。通過模擬的含沙量序列與實測含沙量序得出誤差序列，并采用遞推公式對誤差自回歸實時校正模型的參數進行估計。誤差自回歸實時校正模型參數的率定結果見表1；確定性系數、沙峰預報值和沙峰滯時如表2所示；同時選用訓練樣本以外的5場 （19860629、19870824、 19890811、 19900710、 20030825）實測泥沙過程進行驗證，對比校正前與校正后的預報結果。驗證結果如圖1～5所示。

表1 誤差自回歸模型參數

表2的分析結果表明:①校正后的沙峰相對誤差均比校正前有所降低 （除了19870824），其中19860629、19900710兩場尤為明顯，并且相對誤差均控制在20%以內；②校正后的沙峰滯時總體較大，甚至比校正前的沙峰滯時還大，預報沙峰出現時間相比于實測沙峰出現時間均有較大偏離；③校正后的確定性系數大幅度提高，除2003025這場的確定性系數為0.687外，其余場次的確定性系數均在0.7以上。另外，圖1～5也表明，校正后的預報含沙量過程與實測含沙量過程線擬合程度比校正前擬合程度更好。通過以上分析可知，校正后的泥沙預報精度，較之校正前的預報精度有較大提高。

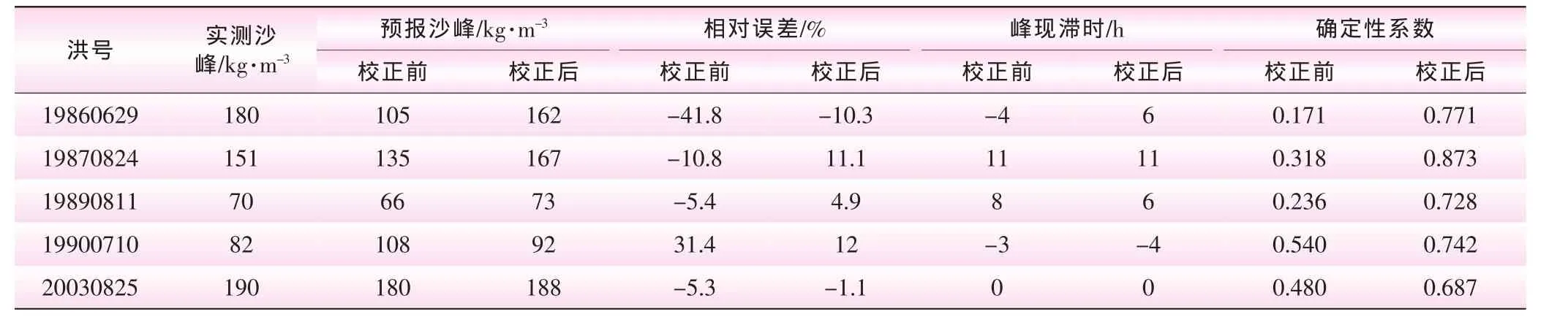
表2 驗證期模型預報校正前、后結果

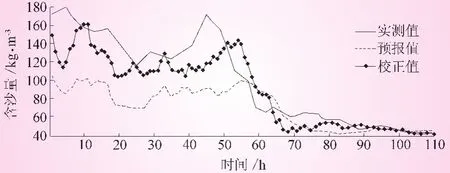
圖1 潼關站 “19860629”場次各序列含沙量過程

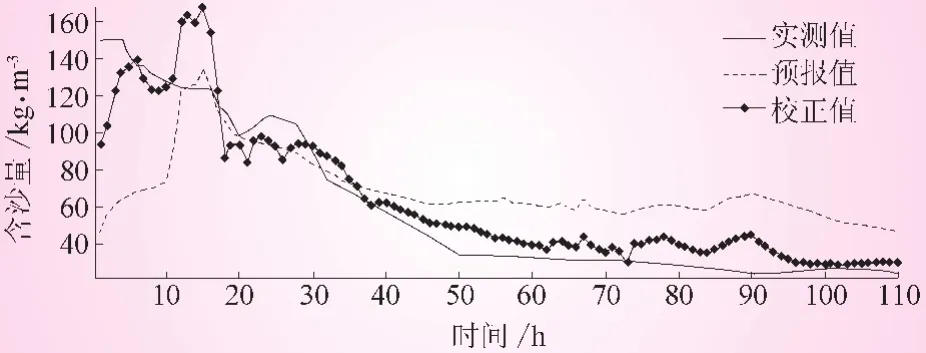
圖2 潼關站 “19870824”場次各序列含沙量過程

圖3 潼關站“19890811”場次各序列含沙量過程

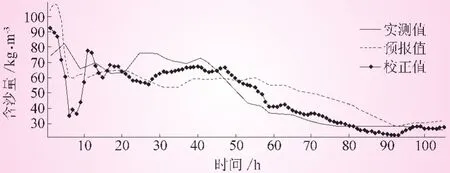
圖4 潼關站“19900710”場次各序列含沙量過程

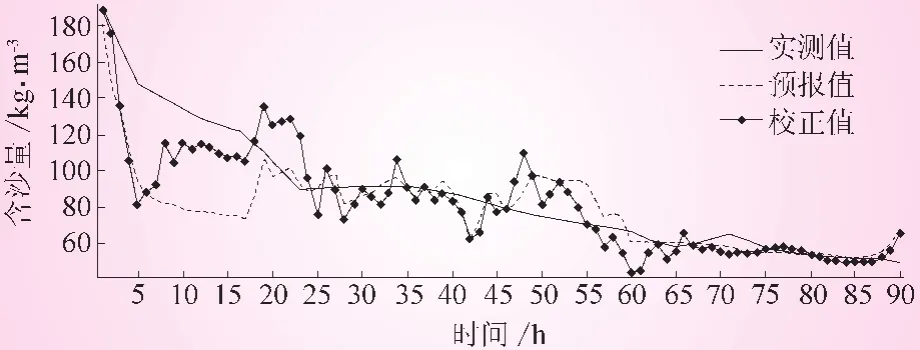
圖5 潼關站“20030825”場次各序列含沙量過程

4 結語

（1）在分析黃河流域龍門—潼關區域河流產沙規律的基礎上，建立以龍門站、河津站、華縣站的含沙量和區間降水為輸入，拓撲結構為4-6-1的BP網絡模型。同時，為了改善BP模型的預報精度，根據誤差序列建立了誤差自回歸模型，對BP網絡的預報結果進行校正，并將該模型應用于潼關站沙量過程的模擬預報。

（2）應用結果表明，校正后的泥沙預報精度，較校正前的預報精度有了較大提高。校正后的沙峰相對誤差均控制在20%以內，其中，19860629和19900710號泥沙過程的沙峰相對誤差分別由校正前的-40.1%和31.4%降低到校正后的-10.3%和12%；同時，校正后的確定性系數均在0.68以上，5場驗證洪水的平均確定性系數由校正前的0.35提高到校正后的0.76，預報精度整體上有顯著提高；另外，單場次泥沙預報精度也大幅提高，如19860629和19870824號泥沙過程，確定性系數由校正前的0.171和0.318提高到校正后的0.771和0.873。

（3）校正前后，5場泥沙模擬預報的沙峰滯時均偏大 （除20030825外）。這可能與模型構建時，取各場次泥沙過程中各控制站沙峰傳播時間和區間降雨的影響滯時的均值作為模型總體的沙峰傳播時間和降雨影響滯時有關。針對這一不足，在未來泥沙過程預報中尚需進一步研究改進。

［1］金雙彥.黃河中下游泥沙預報模型研究［D］.南京:河海大學，2007，12.

［2］李懷恩，樊爾蘭，沈晉，等.逆高斯分布瞬時輸沙單位線模型［J］.水土保持學報， 1994， 8（2）:48-55.

［3］石寶，秦毅，凌燕.響應函數模型在含沙量預報中的應用［J］.水土保持通報， 2008， 28（2）:104-105.

［4］包為民.概念性匯沙模型初探［J］.河海大學學報， 1990， 18（6）:24-29.

［5］毛倩倩，梁忠民，霍世青，等.黃河中游龍門含沙量過程統計預報模型研究［J］.水電能源科學， 2012， 30（4）:83-86.

［6］竇國仁.潮汐水流中懸沙運動及沖淤計算［J］.水利學報，1963（4）:13-24.

［7］梁國亭，錢意穎.黃河泥沙數學模型的研究及應用［J］.水文，2000， 22（9）:7-9.

［8］陳集中.應用人工神經網絡BP模型預測烏江流域年平均含沙量［J］.水文， 2005， 25（4）:6-9.

［9］張小峰.流域產流產沙BP網絡預報模型的初步研究［J］.水科學進展， 2001， 12（1）:17-22.

［10］田景環，王文君，徐建華.基于BP算法的龍門站含沙量預報模型［J］.人民黃河， 2008， 30（3）:26-27.

［11］李正最，謝悅波.基于支持向量機的洞庭湖區域水沙模擬［J］.水文， 2010， 30（2）:44-49.

［12］陳麗華，臧榮鑫，王宏偉.人工神經網絡及其在水質信息檢測中的應用［M］.北京:國防工業出版社，2011.

［13］苑希民，李鴻雁，劉樹坤，等.神經網絡和遺傳算法在水利科學領域的應用［M］.北京:中國水利水電出版社，2002.

［14］苑希民，劉樹坤，陳浩.基于人工神經網絡的多泥沙洪水預報［J］.水科學進展， 1999， 10（4）:393-398.

［15］李允軍，李春紅.三峽上游洪水預報實時校正方法應用比較［J］.水電自動化與大壩檢測， 2009， 33（6）:73-76.

［16］賀莉，傅旭東.黃河吳堡—潼關河段洪水傳播時間的沿程分布［J］.南水北調與水利科技， 2012， 10（1）:18-21.