水文纜索法測流懸索偏角(10°＜θ＜45°)與水深d的分析及推求

秦 敏

( 大慶水文局，黑龍江 大慶163316)

本文以橋測法為例( 船測法類同) ，同時對纜道法施測與求解水深的有關因素作必要的論述。依據水文纜道規范［1］和纜索法施測水深規程和原理，運用有關水文學、流體力學等理論，結合工作實踐經驗，對懸索偏角( 10° ＜θ ＜45°) 時對水深的影響有關因素進行研究，給出由定性到定量的較詳盡的分析與計算公式。通過本站或代表性站，按要求施測出懸索偏角θ 值，借以建立求解懸索偏角和水深的相關理論和一系列適用的模型化公式與圖表。

1 纜索法測流懸索偏角θ ≤10°時求解水深公式的建立

采用纜索法測流，計數器只能間接地測出部分水深，投產前須按要求測試、率定出有關參數，建立不同施測方式的求解水深公式［2］。

1) 無信號系統，采用鉛魚底剛接觸水面計數器對零，下放至鉛魚底剛接觸河底，( 不失重的臨界狀態) 理論型求解水深d 公式:( 下同)

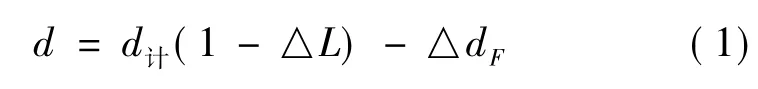
式中: d計為某垂線計數器測得水深，m; △dF為鉛魚入水后因浮力產生向上位移，m; 橋測法因鉛魚體積小，且懸索支點s 固定，故取△dF=0; 纜道法因鉛魚體積較大，浮力主要引起產生主索垂度向上位移，一般鉛魚自重為(75 ～150) kg，試驗值△dF≈(0.04～0.08) m。△L 為在測深狀態下施放一定實量懸索長度L 與相應的計數器讀數每米絕對誤差，m。

△L 的計算公式為:

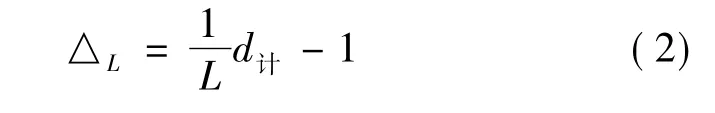
2) 無信號系統采用流速儀中軸對準水面，計數器對零，下放至鉛魚底剛接觸河底，( 不失重的臨界狀態) 理論型求解水深計算公式為:

式中: △d 為鉛魚底至流速儀中軸高，m。

3) 有信號系統，剛收到水面信號，( 鉛魚體位于水中約一半，流速儀位于水面以上) 計數器對零，下放鉛魚至剛收到河底信號，( 不失重的臨界狀態) 求解水深計算公式的建立。

a) 經驗型計算公式為:

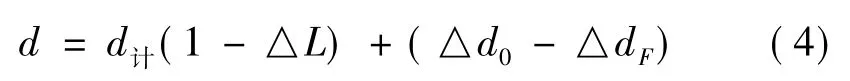
式中: △h 按要求經比測、率定計算的某一水位級的垂線水深改正數，m。

b) 理論型計算公式為:

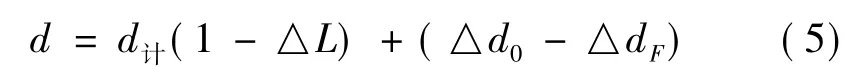
式中: △d0為收到水面信號時托板底至水面平均高，m;其余符號意義同上，纜道站一般鉛魚重( 75 ～150) kg，試驗值△dF≈(0.02 ～0.05) m。

2 懸索偏角(10°＜θ ＜45°)時測深設備系統與水流相互作用下的力學特性及其公式的建立［3］

2.1 懸索偏角( 10° ＜θ ＜45°) 時測深設備系統與流速作用受力情況的分析［4］

以橋測法為例，( 其余兩種測深法略同) 采取常用的流速儀中軸對準水面測深法做初步分析。懸索偏角(10° ＜θ ＜45°) 時測深設備系統受水流受力見圖1。

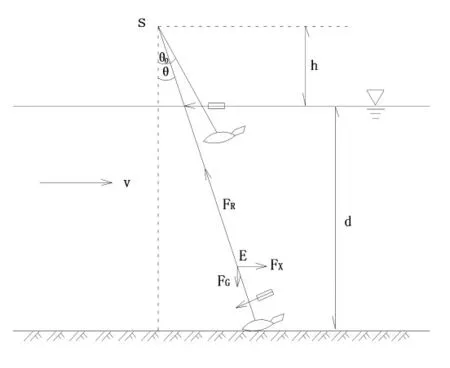
圖1 懸索偏角(10° ＜θ ＜45°)時測深設備系統受水流沖力受力示意圖

如圖1 所示，在施測水深過程中，下放當鉛魚剛至河底，此時鉛直重力在水中的重量為FG( kg) ，水流水平總沖力為Fx( kg) ，懸索拉力為FR( kg) ，合外力為零時受力作用點為E 點，懸索偏角為θ。

2.2 懸索偏角( 10° ＜θ ＜45°) 時測深設備系統受力作用點E 位置及懸索形狀的分析

根據有關水文專業、流體力學等理論，懸索偏角θ 于作用在入水測深系統與水流的正投影面積同流速的平方之積成正比，于鉛魚在水中的重力成反比。一般河流如鉛魚自重15 kg，豎軸直徑0.094 m，流速儀旋漿直徑0.12 m，懸索直徑0.005 m，將按要求實測的懸索偏角(10° ＜θ ＜45°) 的各垂線相對水深與流速分布曲線及有關水文因素進行概化，依據其相似性和相關性原理，假如某站按要求實驗水位區間的各垂線平均水深d =3.00 m，作用于懸索上的平均流速( 取垂線平均流速V) V1，作用于流速儀和鉛魚與水流垂直投影面積之和上的垂線平均流速V2=，取f =0.6 ，各垂線平均懸索偏角=18°，應用本文公式及有關力學理論，計算出受力作用點E 約位于d，如采用纜道測深，鉛魚自重為150 kg，懸索直徑為0.006 m，其余水文因素不變，受力作用點E 約位于0.1 d，相應懸索平均偏角

當懸索偏角一定時，作用于懸索上及流速儀至鉛魚兩部分的水平沖力可視為常量，雖前者但后者受力面積遠大于前者，即A2＞A，經計算FX2＞FX1，因測深設備系統屬于理想的流線型鋼性受力體，綜上所述:當θ ＜45° 時可視為懸索呈線性狀態，只有鉛魚處于失重時懸索才會呈曲線變化，當θ ＞45° 要更換加重鉛魚使θ ＜45° 。

3 求解懸索偏角(10°＜θ ＜45°)時公式等法的建立

3.1 懸索偏角(10° ＜θ ＜45°) 時的理論公式建立

如圖1 所示，某一代表性測深垂線( 無冰情、水草、漂浮物等影響) ，當收到河底信號時懸索偏角(10° ＜θ ＜45°) 的表達式為:

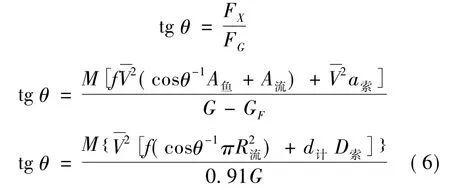
式中: G 、GF為某垂線測深鉛魚自重、鉛魚全入水時的浮力，kg; M 為采用一定的測深設備系統，由按要求實驗測得各水深相應的懸索偏角求得推求θ 值的模比系數，kgs2/m4; f 為相應于M 的各垂線流速儀至鉛魚區間的平均流速V2與相應垂線平均流速V 比值的均值; A魚為采用測深鉛魚豎軸橫截面積，m2; A流為流速儀旋漿有效面積，m2; ( 參考儀器吊環等面積仍取A流= πR2流) ; a索為相應于M 記數器計數水深d計與水流的正投影面積，m2;( a索= cosθd計D索，因該值對θ 值影響較小，為計算方便取a索≈d計D索) ;R魚、R流、D索為鉛魚豎軸半徑，流速儀旋漿半徑、懸索直徑( m) 。

3.2 求解懸索偏角(10° ＜θ ＜45°) 時的公式法

通過本站或代表性站，按要求實測出≥30 次且有代表性的垂線懸索偏角(10° ＜θ ＜45°) ，將(6) 式轉換成求解懸索偏角公式。

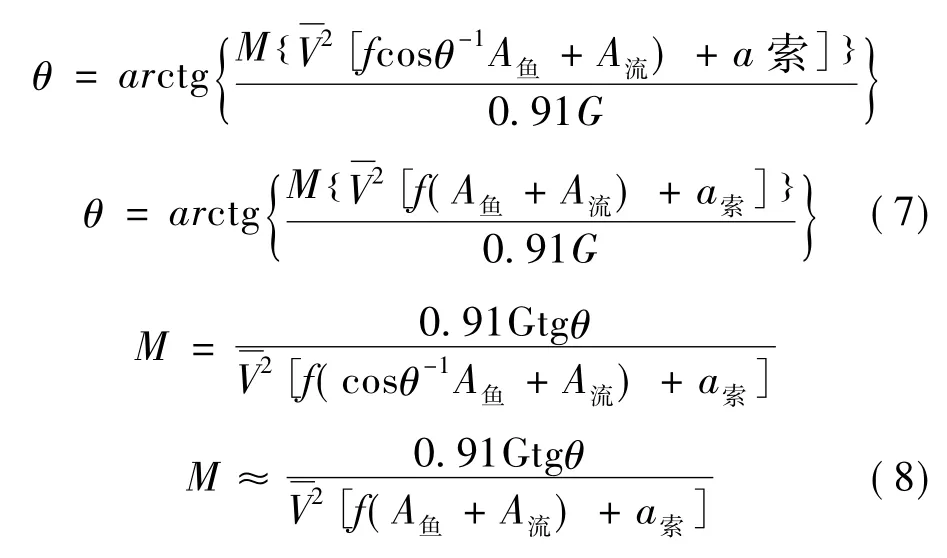
采用A 或cosθ－1計算得二者M 值相近，為計算方便取A魚≈cosθ－1A魚。

3.3 求解懸索偏角(10° ＜θ ＜45°) 模比系數M 的圖解法

公式(8)中如施測水深設備系統不變，且f 值為常數，當水深和懸索偏角一定時M 值與成反比，可采用列表法求出以水深d 為參數的三變數關系曲線圖，如圖2 所示。(為計算方便可取d ≈d計)

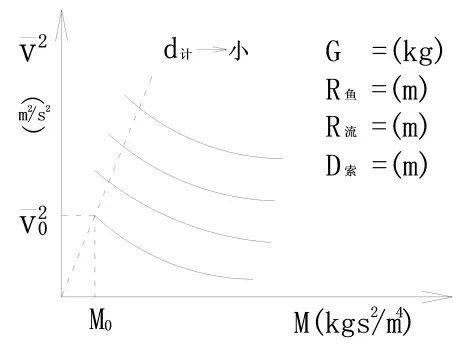
圖2 懸索偏角(10° ＜θ ＜45°)時求解其摩比系數M(10° ＜θ ＜45°)三變數關系曲線示意圖

3.4 采用列表法求解懸索偏角(10° ＜θ ＜45°)

應用(6) 式采用列表法求解懸索偏角，在實驗的水位區間A魚、A流、G、f 為常數，M 值可由圖(8) 查得，已知( 可用d 代替) 等值即可快速計算出相應的Q 值，見表1。

表1 求解懸索偏角(10° ＜θ ＜45°)計算成果表

3.5 求解懸索偏角(10° ＜θ ＜45°) 的圖解法

可建立垂線水深d計為參數的垂線平均流速與懸索偏角三變數關系曲線圖，如圖3 所示。

圖3 求解懸索偏角(10° ＜θ ＜45°)時(10° ＜θ ＜45°)三變數關系曲線示意圖

4 更換測測深鉛魚等設備時求解懸索偏角(10°＜θ ＜45°)的公式法等法的建立

4.1 更換測深設備時經實驗、率定求解懸索偏角(10° ＜θ ＜45°) 的公式法及圖解法［5］

橋測法當高水位及水深、流速較大時期，為系統減少懸索偏角θ 值，以減少其測量與計算工作量，時常要更換加重鉛魚及懸索，有條件的站或改為纜道施測。此時同一測深垂線當水深、流速一定時，因鉛魚在水中的重量增加△FG，相應的鉛魚及懸索與流速的正投影面積各增加△A魚、△a索，理論與計算表明△FG對θ 值產生主要影響，故θ2＜θ1，摩比系數M2＞M1。采用(8) 式計算出按要求實驗的水位區間各垂線的M 值，繪制出相關的與三變數關系曲線圖，再采用(7) 式求解出實驗水位區間的各測深垂線的θ 值。

4.2 更換測深鉛魚等無條件比測時求解懸索偏角(10° ＜θ ＜45°) 的公式法及圖解法

根據更換前后的測深鉛魚細長比具有一定的比例性，且施測水深和流量的總體型式方法不變，可假定同一測深垂線當θ2= θ1時，模比系數M2≈M1，因△FG對Q 值起主要作用，顯然可應用更換測深設備前原實驗、率定分析的各測深垂線θ、M、f、A流參數，將更換鉛魚等后的G2、( A魚)2、( a索)2代入(9) 式即采用逆運算法求解出各相應的垂線平均流速繪制出與θ) 三變數關系曲線圖，故已知查得M 將原f與G2、( A魚)2、( a索)2等數值代入(7) 式，采用列表法便可求解出更換測深鉛魚后各垂線相應的懸索偏角θ 值。

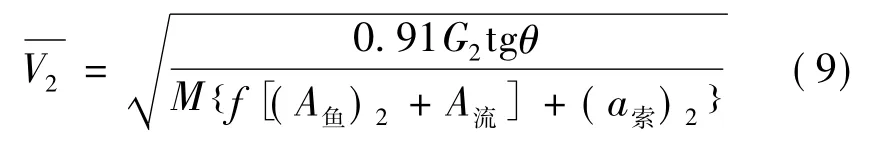
式中: Q、M、f 為同更換測深鉛魚等設備前( 經原實驗率定、分析求得) ; A魚)2、( a索)2更換測深鉛魚、懸索后于水流的正投影面積，m2。

5 懸索偏角(10°＜θ ＜45°)時求解水深d 公式等法的建立

5.1 懸索偏角θ 與θ0相應時二懸索干繩之差△L干及纜道法施測水深引起位移增量△d位對水深影響的分析，如圖1 所示，△L 計算公式為:

式中: h 為相應于△L干懸索支點s 至水位間高差，m。采用橋測法無信號系統施測水深方法，施測水深過程中施放懸索長度與記數水深( dθ)計完全同步運行，故某一垂線測得的改正前水深dθ為懸索偏角θ時流速儀豎軸與水面交點至鉛魚底的測深設備系統的斜線長度dθ。dθ計算公式為:

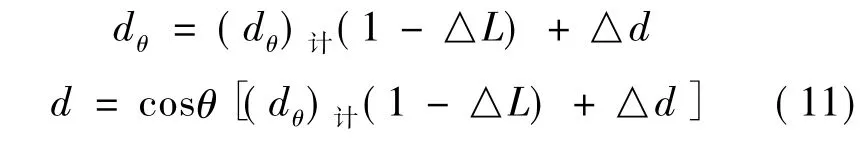
當△L 為正時相當于dθ+ △L干，此時鉛魚將處于失重，導致懸索松動，需上提鉛魚△L，反之鉛魚沒觸及河底則須下放鉛魚△L干才能使得測深系統達到規定的測深狀態。即施測水深過程中當θi= θ時提或放鉛魚的累積調整數△L 已隱含于( dθ) 中。另從(10) 式可看出，因θ0、θ 與h 無關，當某一測深垂線θ0、θ、dθ一定時，而△L干與h 成正比為變數顯然不合理，故△L干不再參加對dθ的訂正。

同理，經本文有關論述及計算，采用有信號系統的纜道法施測水深，如纜道鉛魚自重G =150 kg，采用θ0與θ 的最大隨機變差△θ 計算合外力增量，由△FR≤8 kg，由△FR引起的主索位移增量△d位很小，可忽略不計。采用有信號系統推求偏角改正前的理論水深d'θ公式為:

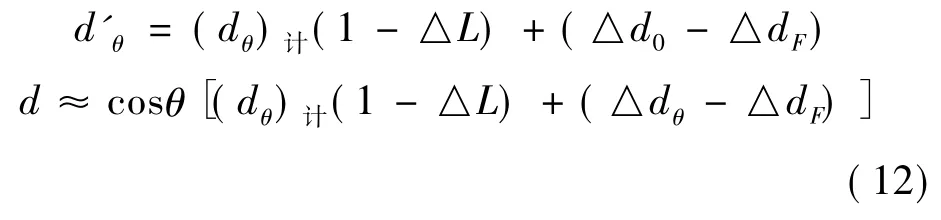
5.2 懸索偏角( 10° ＜θ ＜45°) 時采用列表法求解垂線水深d

1) 無信號系統施測水深法，懸索偏角( 10° ＜θ＜45°) 時采用列表法求解垂線水深d，計算過程見表2。

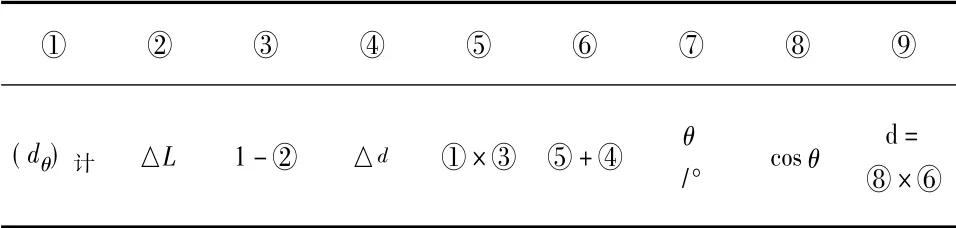
表2 無信號系統列表法求垂線水深過程表 m

5.2.2 有信號系統施測水深法，懸索偏角( 10°＜θ ＜45°) 時采用列表法求解垂線水深d 表，過程見表3。

表3 有信號系統列表法求垂線水深過程表 m

采用纜索法測深、測流其影響因素諸多，成因較復雜，技術性較強，受其測驗設備、測試方法、水流條件、力學特性等影響，各環節有機聯系、相互制約，如某一參數理解不清或測試方法不正確，易出現人為差錯，對相關的資料成果產生絕對誤差和系統誤差。

本論文將討論問題的焦點定格于施測水深收到水 面 與 河 底 二 信 號 區 間 的 有 關θ0、θ、△d、△d0、△dF、( dθ)計、△L 等有關常量與增量因數的定性分析與定量歸納。對△L干、△d位等提出與以往書刊略不同的見解，推求建立測深設備型式相同而測深方式、方法不同時相應的求解水深d 公式及圖表。

可通過本站或代表站實驗的懸索偏角等資料，應用θ、d計和入水測驗設備的幾何形狀、尺寸及重量，運用有關理論建立起的相應公式，經概化、分析、率定出f、M，經必要的計算驗證，進而引深建立起求解更換測深鉛魚等設備前后的一系列模型式求解懸索偏角θ、M 實用性公式和圖表。

6 結 語

提高水文測深、測流精度，減少不便施測懸索偏角的工作量，將其轉換成內業工作，利于流量等測驗。方法可用于修正 漏測懸索偏角的歷史洪水資料，供設計、計算水利等工程應用。

當遇于本文立論不符的水文條件時仍需施測懸索偏角。本文作為從事水文測洪的工程技術人員應用時借鑒與參考。

［1］中華人民共和國水利部. SL443—2009 水文纜道測驗規范［S］. 北京: 中國水利水電出版社，2009.

［2］嚴順義. 水文測驗學［M］. 北京:水利水電出版社，1984.

［3］上海市物理學會. 流體力學［M］. 上海:上海教育出版社，1981.

［4］畢潔光. 高中力學題解指南［M］. 北京:知識出版社，1983.

［5］肖明耀. 誤差理論與應用［M］. 北京:計量出版社，1985.