羅茨風(fēng)機(jī)出口加裝止回平衡閥預(yù)防風(fēng)機(jī)停車時(shí)倒轉(zhuǎn)
郭士才 楊 彬 張世飛
(安徽晉煤中能化工股份有限公司安徽臨泉236400)
?
羅茨風(fēng)機(jī)出口加裝止回平衡閥預(yù)防風(fēng)機(jī)停車時(shí)倒轉(zhuǎn)
郭士才 楊 彬 張世飛
(安徽晉煤中能化工股份有限公司安徽臨泉236400)
脫硫羅茨風(fēng)機(jī)停運(yùn)或緊急停車過(guò)程中,由于管道系統(tǒng)出口壓力高于進(jìn)口壓力,無(wú)法控制可燃?xì)怏w倒流,風(fēng)機(jī)瞬間發(fā)生倒轉(zhuǎn)導(dǎo)致葉輪破碎,極易產(chǎn)生可燃?xì)怏w泄漏;如果葉輪破碎產(chǎn)生火花就會(huì)發(fā)生可燃?xì)怏w著火、爆炸和環(huán)境污染,給企業(yè)造成巨大經(jīng)濟(jì)損失。為使脫硫羅茨風(fēng)機(jī)在開(kāi)、停機(jī)過(guò)程中更合理、更安全穩(wěn)定運(yùn)行,在風(fēng)機(jī)出口加裝止回平衡閥,預(yù)防羅茨風(fēng)機(jī)停車時(shí)倒轉(zhuǎn)。
1 羅茨風(fēng)機(jī)止回平衡閥
羅茨風(fēng)機(jī)止回平衡閥主要由閥體、舌管、閥板連接體、觀察口、檢查清理口、排污管、平衡閥、密封板、閥板等組成。羅茨風(fēng)機(jī)止回平衡閥加工構(gòu)造、原理及具體作用如下。
1.1 閥體
根據(jù)羅茨風(fēng)機(jī)出口直徑大小而定,對(duì)于Φ600 mm的出口止回閥一般用Φ1 200 mm、長(zhǎng)度1 500 mm、厚度10~12 mm、Q235無(wú)縫管材加工制成承壓50 kPa的容器,前端有一段法蘭連接管,連接管與羅茨風(fēng)機(jī)出口直徑大小一致,法蘭和風(fēng)機(jī)出口法蘭配套,后端有法蘭和盲板蓋組成。
1.2 舌管
采用Φ800mm的Q235無(wú)縫管材,在閥體前端內(nèi)部焊接,由于在運(yùn)行過(guò)程中,閥板不完全被掀起,防止對(duì)氣體產(chǎn)生阻力,舌管直徑設(shè)計(jì)要大于連接管直徑,尾端焊接與閥板密封面直徑一致密封面板,防止大小不吻合產(chǎn)生漏氣,尾端密封面板傾斜度與垂直線夾角5°為宜,在舌管上方焊接閥板連接機(jī)構(gòu)以便安裝閥板。
1.3 閥板連接結(jié)構(gòu)
由閥銷和銷套管組成,閥板連接體采用高壓耐磨套管和不銹鋼材質(zhì)的閥銷制成,安裝在舌管上方。由于在風(fēng)機(jī)止回閥內(nèi)部的閥板長(zhǎng)期受風(fēng)機(jī)的風(fēng)力吹動(dòng),銷釘易被磨損、腐蝕,造成脫落。使用高壓套管和不銹鋼材質(zhì)銷釘既耐磨又耐腐蝕,消除了在使用過(guò)程中由于磨損或腐蝕而致使閥板脫落的現(xiàn)象。
1.4 觀察口
觀察口正對(duì)閥板連接體,主要是便于更換和觀察風(fēng)機(jī)內(nèi)部閥板連接體的磨損情況,觀察口孔徑按合適的尺寸進(jìn)行開(kāi)口,采用方形(或圓形)短接和頂部盲板組對(duì)而成,嚴(yán)格按加工技術(shù)規(guī)范要求進(jìn)行焊接,使其更有利于拆卸和觀察,更大程度上消除由于連接體不便于檢查、維修以及閥板脫落的安全隱患。
1.5 檢查清理口
止回閥末端設(shè)置檢查清理口,采用符合規(guī)范的法蘭盲板連接,不僅更符合加工技術(shù)規(guī)范,而且更便于拆除清理止回閥內(nèi)部積垢。由于受工藝的影響,氣體產(chǎn)生波動(dòng),正對(duì)風(fēng)向的末端底板直接受力,易產(chǎn)生焊縫撕裂而發(fā)生爆燃,必須按壓力容器和盲板設(shè)計(jì)規(guī)范標(biāo)準(zhǔn)進(jìn)行施工。
1.6 排污管
由于系統(tǒng)氣體帶有少量液體,或停車蒸汽置換產(chǎn)生少量的水,如果不及時(shí)排除,會(huì)造成設(shè)備殼體帶水,影響設(shè)備正常運(yùn)行和系統(tǒng)穩(wěn)定生產(chǎn),將系統(tǒng)產(chǎn)生的水經(jīng)過(guò)排污管及時(shí)排出可保護(hù)設(shè)備和生產(chǎn)正常進(jìn)行。
1.7 平衡閥
連接舌管和閥體外殼,在正常開(kāi)車過(guò)程中閥門處于關(guān)閉狀態(tài)。開(kāi)車時(shí),需要進(jìn)行羅茨風(fēng)機(jī)盤車,為了盤車正常運(yùn)行,打開(kāi)平衡法讓系統(tǒng)帶有50 kPa壓力的氣體慢慢倒過(guò)來(lái)(出口壓力遠(yuǎn)遠(yuǎn)小于10 kPa),帶動(dòng)風(fēng)機(jī)葉輪運(yùn)轉(zhuǎn)盤車, 盤車運(yùn)轉(zhuǎn)正常關(guān)閉平衡閥門后方可開(kāi)車。
羅茨風(fēng)機(jī)止回平衡閥結(jié)構(gòu)示意見(jiàn)圖1。
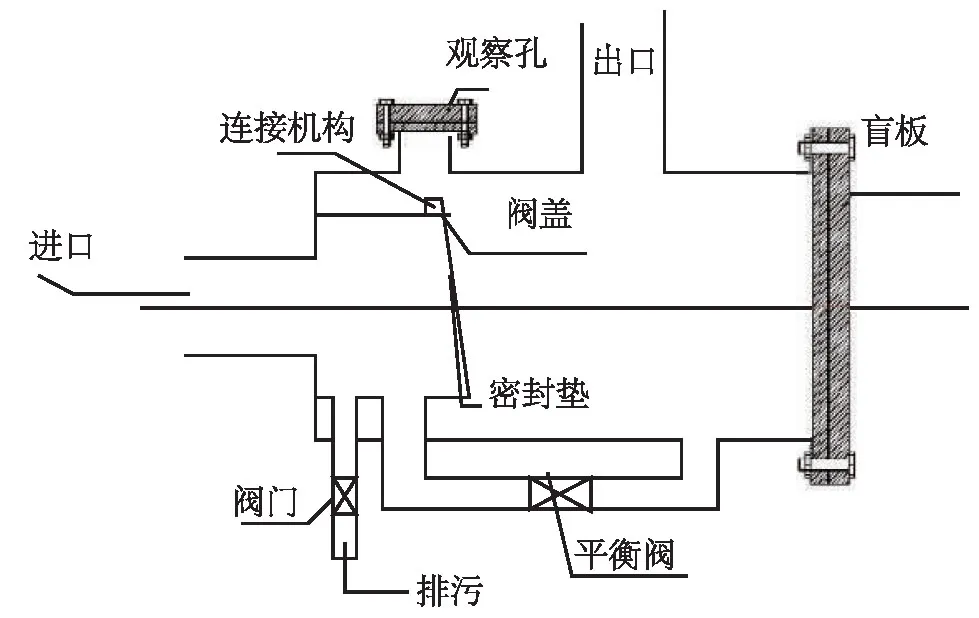
圖1 羅茨風(fēng)機(jī)止回平衡閥結(jié)構(gòu)示意
2 工作原理
氣體由羅茨風(fēng)機(jī)出口,通過(guò)與止回平衡閥進(jìn)口法蘭連接,進(jìn)入止回平衡閥舌管,由于氣體壓力
將打開(kāi)閥板,氣體進(jìn)入閥腔,通過(guò)閥門出口連接進(jìn)入生產(chǎn)系統(tǒng);當(dāng)停機(jī)時(shí),由于進(jìn)口壓力變小,閥板因重力作用而回落,壓住舌管密封面,阻隔了倒流的系統(tǒng)氣體,避免了羅茨風(fēng)機(jī)葉輪回轉(zhuǎn),保護(hù)了葉輪殼體。
3 使用效果
羅茨風(fēng)機(jī)止回平衡閥設(shè)計(jì)簡(jiǎn)單、工藝符合化工生產(chǎn)要求,安裝在羅茨風(fēng)機(jī)的出口端,起到防止帶有壓力氣體(液體)倒流,而排污閥又能防止羅茨風(fēng)機(jī)帶水運(yùn)行,穩(wěn)定了生產(chǎn)系統(tǒng)的運(yùn)行,平衡閥的開(kāi)啟,方便了開(kāi)車前的盤車;減少了人工操作盤車,后端盲板能夠便于拆卸清理閥體的積垢,保證了設(shè)備長(zhǎng)周期、穩(wěn)定運(yùn)行,使羅茨風(fēng)機(jī)在安裝上更科學(xué),使用中更合理、更安全;保障生產(chǎn)系統(tǒng)穩(wěn)定運(yùn)行,同時(shí)也提高了生產(chǎn)經(jīng)濟(jì)效益。
2015- 11- 09)

