構造
——數學競賽解題的“鑰匙”

●

(松江區第二中學 上海 201600)

構造
——數學競賽解題的“鑰匙”

●繆雪松

(松江區第二中學 上海 201600)

“問題是數學的心臟”，數學離不開問題的解決．就數學競賽活動而言，學生在學習數學競賽知識、掌握數學競賽技能、領悟數學競賽思想的過程中，需要解決大量的數學問題．學生獨立地分析、解決數學問題的過程，無論是真創造還是類創造，都是一個創造的過程，這樣的過程對學生創新能力、實踐能力的培養大有裨益．學生在解決數學競賽問題的過程中，常常會遇到一道道的“關卡”，而“構造”這一策略，便成了突破解題障礙、打通道道“關卡”的神奇鑰匙．在復雜的問題背景下，抽取問題的本質屬性，尋找到數學知識內在的聯系，常常能創造性地構造出新的、簡單的數學模型，從而得到原問題的奇思妙解，這就是“構造”的精髓．

本文擬從以下7個方面向讀者展現“構造”的無窮魅力．

1 構造代數式

例1已知a+b+c=a2+b2+c2=2，求證：

a(1-a)2=b(1-b)2=c(1-c)2．

分析求證的等式中的各式，恰好是多項式x(1-x)2中的x分別取a,b,c時的值．因此，本題可轉化為證明當x分別取a,b,c時，x(1-x)2的值不變．由于x(1-x)2是關于x的三次多項式，且注意到題設條件，因此可構造三次式(x-a)(x-b)(x-c)，建立它與x(1-x)2之間的某種關系．

證明因為

(a+b+c)2=a2+b2+c2+2ab+2bc+2ca,

又

a+b+c=a2+b2+c2=2,

所以

4=2+2ab+2bc+2ca，

從而

ab+bc+ca=1.

于是

(x-a)(x-b)(x-c)=

x3-(a+b+c)x2+(ab+bc+ca)x-abc=

x3-2x2+x-abc,

即

x(1-x)2=(x-a)(x-b)(x-c)+abc.

由此可見，當x分別取a,b,c時，x(1-x)2的值都是abc,因此a(1-a)2=b(1-b)2=c(1-c)2.

評注本題構造了三次式(x-a)(x-b)(x-c)，然后建立它與x(1-x)2之間的關系，再通過賦值來證明．

圖1

2 構造復數

解設廠址的位置為Z，則Z到3個村莊的供水管道長為

d= |OZ|+|AZ|+|BZ|=

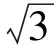
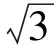
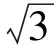
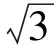
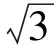
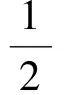
評注本題也可直接利用費馬點的有關結論處理．

3 構造數組

例3已知集合A中有49個正整數，它們的約數都是不大于10的質數．求證：其中必有4個整數的乘積是一個整數的4次方．

證明A中的任一元素必可以表示為xi=2αi3βi5γi7δi(i=1,2,…,49)的形式，記xi=(αi,βi,γi,δi)，當且僅當xi=(αi,βi,γi,δi)與xj=(αj,βj,γj,δj)中各個坐標的奇偶都相同時xi·xj=y2(其中y是正整數)，而各坐標的奇偶不全相同的數組最多有24=16個．由抽屜原理可知，每17個不同數組中至少有一對數組對應奇偶均相同．

顯然，y1,y2,…,y17這17個數都可以表示成2αi3βi5γi7δi的形式，在y1,y2,…,y17這17個數中，必存在2個數ym,yn滿足ym·yn=p2(p為正整數)，則與ym,yn對應的集合A中的4個元素之積即為p4．

4 構造關系

例4已知{a1,a2,…,a2 013}是由2 013個質數構成的集合，b1,b2,…,bn∈{a1,a2,…,a2 013}，則乘積b1b2…bn共有多少個不同的值？

解法1(構造不等關系)

不妨設b1≤b2≤…≤bn．原問題等價于：求滿足b1,b2,…,bn∈{1,2,…,2 013}的數組{b1,b2,…，bn}的個數，構造

1≤b1

解法2 (構造順序關系，即隔板法)

原問題等價于：將編號為1,2,…,n的小球放入編號為1,2,…，2 013的盒中，要求序號大的球放入盒子的編號不小于序號小的球放入盒子的編號，求放法的總數．

5 構造映射

例5把△ABC的各邊n等分，過各分點分別作各邊的平行線，得到一些由三角形的邊或這些平行線所組成的平行四邊形，試計算這些平行四邊形的個數．

圖2

解根據對稱性，可先考慮邊不平行于BC的小平行四邊形．如圖2所示，把AB和AC各延長一等分至點B′，C′，聯結B′C′．將與AB′平行的n條線分別延長，與B′C′相交得到n個交點，這n個交點與點B′，C′作為線段B′C′的n+2個分點，從點B′至點C′依次記為1，2，…，n+2．圖2所示的小平行四邊形所在4條直線分別交B′C′于點i，j，k，l．記A={邊不平行于BC的小平行四邊形}，B={(i,j,k,l)|1≤i

6 構造函數

例6已知a1+a2+a3=b1+b2+b3，a1a2+a2a3+a3a1=b1b2+b2b3+b3b1，min{a1,a2,a3}≤min{b1,b2,b3},求證：max{a1,a2,a3}≤max(b1,b2,b3)．

(2008年北京大學自主招生試題)

證明設a1+a2+a3=b1+b2+b3=-A，

a1a2+a2a3+a3a1=b1b2+b2b3+b3b1=B，

且不妨設a1≤a2≤a3,b1≤b2≤b3，設

f(x)= (x-a1)(x-a2)(x-a3)=

x3+Ax2+Bx+C1，

g(x)= (x-b1)(x-b2)(x-b3)=

x3+Ax2+Bx+C2.

因為a1≤b1，f(a1)=0，而g(a1)≤0，所以C2≤C1.又f(a3)=0，于是

g(a3)=f(a3)+C2-C1≤0，

即

(a3-b1)(a3-b2)(a3-b3)≤0.

若a3>b3，則g(a3)>0，矛盾．因此a3≤b3，即

max{a1,a2,a3}≤max{b1,b2,b3}．

圖3

7 構造幾何體

例7在一圓周上任取3個點構成三角形，求該三角形是銳角三角形的概率．

解設圓半徑為1，設3個頂點將圓分得的3條弧弧長分別為x,y,z，則x+y+z=2π，其中0

[1] 繆雪松.中國大學自主招生數學補充教程[M].北京：中國出版集團現代教育出版社，2012．