基于SVR的滑坡位移研究

劉小珊 (湖北文理學院數學與計算機科學學院，湖北 襄陽 441053 中國地質大學(武漢)數學與物理學院，湖北 武漢 430074)

羅文強，李飛翱 (中國地質大學(武漢)數學與物理學院，湖北 武漢 430074)

王成勇 (湖北文理學院數學與計算機科學學院，湖北 襄陽 441053)

基于SVR的滑坡位移研究

劉小珊 (湖北文理學院數學與計算機科學學院，湖北 襄陽 441053 中國地質大學(武漢)數學與物理學院，湖北 武漢 430074)

羅文強，李飛翱 (中國地質大學(武漢)數學與物理學院，湖北 武漢 430074)

王成勇 (湖北文理學院數學與計算機科學學院，湖北 襄陽 441053)

滑坡位移具有非線性特征，針對單變量的時間序列，首先引入相空間重構理論，將其擴展到多維的相空間中。再結合數據挖掘中的機器學習算法——支持向量回歸算法(SVR)建立預測模型，并對李家灣滑坡的水平位移進行預測。試驗結果表明，該模型具有非常高的精度(均控制在94%以上)，可以充分的應用于滑坡災害的預測和預報。

滑坡水平位移；相空間重構；支持向量回歸；預測

滑坡是一個極其復雜的非線性動態系統，內部受巖土體屬性的控制，外部受庫水位變動、大氣降雨、地震、人工加載等多種因素的影響。正是這種內外因素相互作用的復雜性和難以預見性，使得滑坡的變形表現出非常復雜的演化特征。

目前，基于時間序列的分析方法是滑坡位移預測工作中相對集中的一個發展方向。傳統的預測方法是直接從單變量的時間序列出發，建立預測模型，分析它的時間演變規律[1-2]。但由于時序數列是許多因子相互作用的綜合反映，蘊含了參與整個運動過程中全部變量的信息，所以單變量的時序數列無法充分的將序列中的信息顯露出來。針對這一問題，筆者首先引入了相空間重構理論，將單變量的數據擴展到多維的相空間中去，從而獲得更多的數據間的關聯關系。然后，應用支持向量回歸算法(Suppert Vector Regression,SVR)[3]對重構后的數據進行建模，并在此基礎上對滑坡的水平位移進行預測。

1 支持向量回歸

1.1相空間重構

為了從時間序列中提取更多的有用信息， Packard等提出用時間序列重構相空間的2種方法：導數重構法和坐標延遲重構法[4]。Takens等提出嵌入定理：對于無限長、無噪聲的d維混沌吸引子的標量時間序列{x(n)}，只要維數m≥2d+1，總可以在拓撲不變的意義上找到一個m維的嵌入相空間[5]。嵌入定理保證了可以從一維混沌時間序列{x(i),i=1,2,3,…,n}中重構一個與原動力系統在拓撲意義下等價的相空間:

X(i)={x(i),x(i+τ),…,x(i+(m-1)τ)}

(1)

式中，i=1,2,…,n-(m-1)τ,n為時序長度；m為嵌入維數；τ為延遲時間。

1.2支持向量回歸算法

支持向量機是一種基于統計學習理論的機器學習算法，其建立在VC維(Vapnik-Chervonenkis Dimension)理論和結構風險最小化原理(Structural Risk Minimization,SRM)基礎上，根據有限的樣本信息在模型的復雜性和學習能力之間尋求最佳折中。

非線性SVR算法基本思想如下：對于給定的n個樣本數據{xn,yn}，其中xn∈Rm的m維向量，yn∈R為相應的輸出變量，引入非線性映射φ，將樣本空間映射入一個高維(以至于無窮維)的特征空間H(Hilbert空間)，從而使在樣本空間中的高度非線性問題在特征空間中可以進行線性回歸。其具體的實現是通過核函數K(xi,xi)=φ(xi)·φ(xj)來實現的。回歸函數表達式如下：

f(x)=(W,φ(xn))+bφ:Rm→HW∈Rm

(2)

與其他回歸分析方法相比，SVR引入了ε-不敏感誤差函數和最優回歸平面(見圖1)，此時所有樣本點到所求超平面的距離都小于ε，這樣尋求最優回歸超平面的問題則轉化為求解如下一個二次凸規劃問題：

(3)

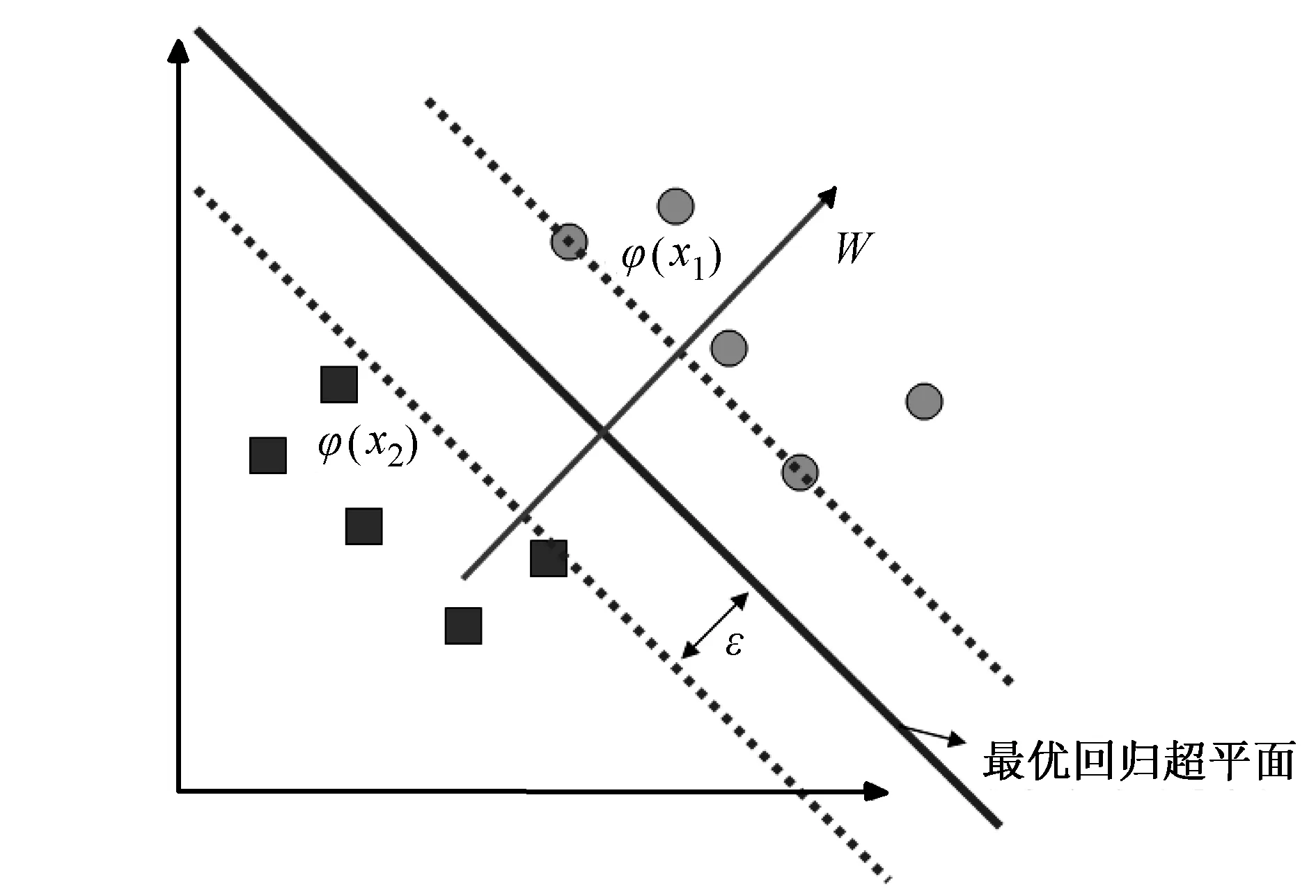
圖1 回歸超平面圖示

但實際問題中往往是有噪音干擾的，不可能將所有的樣本點都落在ε管道中，即便有時能夠達到，隨著ε的減小，也會有個別樣本點“溢出”。為處理函數f在ε精度不能估計的數據，引入松弛變量ξi，則修改上式的目標函數和約束條件，有偏離的點的最優回歸超平面歸結為一個新的二次凸規劃問題[3]：

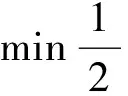
(4)

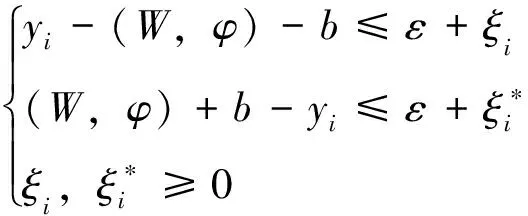
(5)

引入拉格拉日函數和對偶變量：

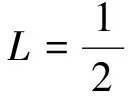
(6)

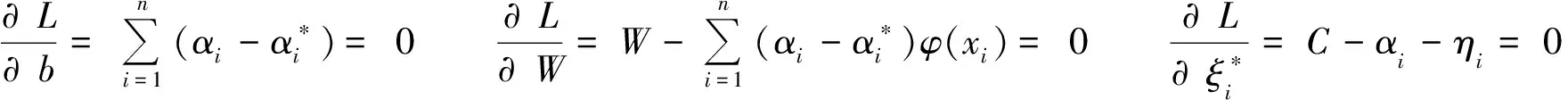
(7)

(8)

式中，核函數K(xi,xj)為滿足Mercer條件的任意對稱函數。由于SVR只考慮高維特征空間的點積運算K(xi,xi)=φ(xi)·φ(xj)，而不是直接使用非線性映射φ，這樣就免去了因為函數φ的未知而無法計算W的表達式。常見的核函數有多項式函數K(xi,xj)=[(xixj)+1]q；高斯徑向基函數(RBF)K(xi,xj)=exp{-|xi-xj|2/2σ2}；Sigmoid函數tanh[v(xixj)+c]等[3,6]。

2 工程實例

2.1數據準備與相空間重構

選取李家灣滑坡的變形監測資料[7]，該資料顯示滑坡的前部、中部、后部監測點的變形分別受不同的因素影響，如降雨量、庫水位、孔隙水等。為研究不同影響因素作用下的滑坡變形預測模型，選取李家灣滑坡主剖面上3個地表位移監測點BD7-35、BD7-36、BD7-37作為研究對象，截取2007-08-08至2009-07-13之間的25組監測數據作為樣本，其中以2007-08-08至2009-02-13之間的20組監測數據作為訓練樣本，2009-03-13至2009-07-13之間的5組監測數據作為測試樣本。

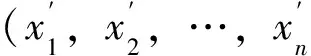
2.2SVR預測模型

數據預處理之后就可以建立基于支持向量回歸算法的預測模型。筆者選擇高斯徑向基函數為核函數，其函數回歸模型可以表示如下[8]：

代入重構后的數據可以得到第n+1點的預測值：

將所得的n+1點的預測值加入訓練樣本，再代入SVR預測模型，即可求出第n+2點的預測值。如此遞推，每預測一步后，將增加的預測值添加到訓練樣本中，同時保持總的訓練樣本數不變，便可得到n+t時刻的預測值：

2.3預測結果分析

將推導的預測模型應用于李家灣滑坡的預測。滑坡剖面分別為BD7-35、BD7-36、BD7-37水平位移監測點的預測值和原始值的比較如圖2所示，精度分析如表1所示。從圖2中可以看出，對于這3個分別受不同影響因素作用下的滑坡剖面，其水平位移預測值的走勢與工程實測值的走勢基本一致，沒有出現異常值，效果良好。從表1中可以看出，對于這3個滑坡剖面水平位移預測值的精度都在94%以上，最高達到99.6%，已經非常逼近實測值。并且從圖2和表1都可以看出，越往后，預測效果越好。

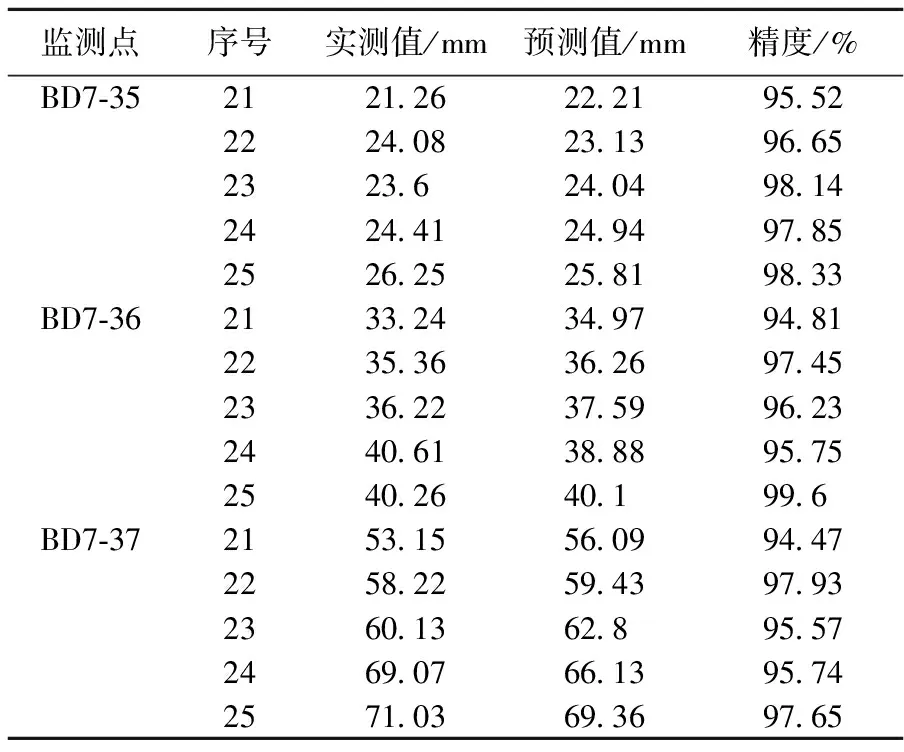
表1 預測精度

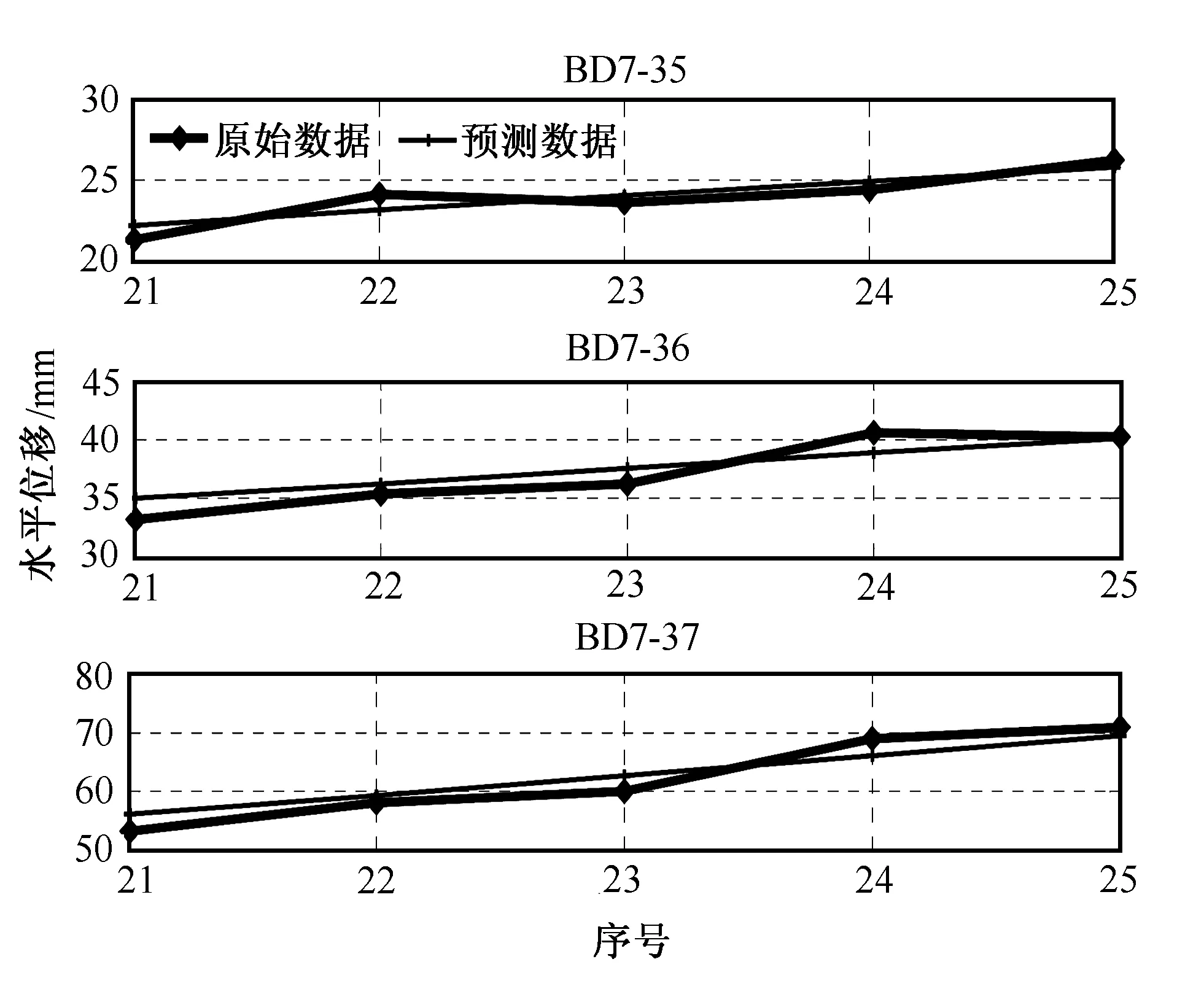
圖2 原始值與預測值的比較

3 結 語

將相空間重構理論與支持向量回歸算法相結合，建立了滑坡水平位移的預測模型，并應用于李家灣滑坡位移的預測。從工程實例中可以看出，這2種理論的結合對滑坡水平位移的預測具有較高的精度，使用該方法可以無需知道巖土結構中的力學過程和機制，對于小樣本、非線性的實際問題可以直接挖掘出時序中各數據的關聯關系，進而進行有效的預測。

[1]張德成，徐則民.滑坡位移的時序分析[J].地球與環境，2011,39(2)：224-230.

[2]鄭加柱,郭斐.變形監測數據的時間序列分析[J].森林工程,2008,24(4):50-53.

[3]陳永義，熊秋芬.支持向量機方法應用教程[M].北京:氣象出版社，2011.

[4]Packard N H,Crutchfield J P,Farmer J D,et al.Geometry from a time series[J].Physical Review Letters,1980,45(9):712-716.

[5]Takens F.Detecting strange attractors in turbulence.In:Dynamical Systerms and Turbulence[M].Berlin:Springer-Verlag, 1981:366-381.

[6]王定成.支持向量機預測與控制[M].北京:氣象出版社，2009.12.

[7]程江濤.庫水變動誘發水庫滑坡變形演化機理及預測研究[D].武漢：中國地質大學(武漢),2011.

[8]董輝,傅鶴林,冷伍明.支持向量機的時間序列回歸與預測[J].系統仿真學報，2006,18(7)：1785-1788.

2012-11-27

國家重點基礎研究發展計劃資助“973”計劃(2011CB710605)。

劉小珊(1989-)，女，碩士生，現主要從事工程概率方面的研究工作。

P642.22；TP391

A

1673-1409(2013)04-0076-03

[編輯] 洪云飛