基于帝國競爭算法的車架優(yōu)化

孫 麗，王 珂，孟廣偉，李 鋒，郝 巖，劉忠振

（1.徐工集團工程機械股份有限公司 建設機械分公司，江蘇，徐州 221002；2.吉林大學 機械科學與工程學院，吉林，長春 130022）

車架作為汽車的主要部分，承載著汽車發(fā)動機及其它各個部件。為了尋求既安全又經濟的結構形式，汽車車架輕量化設計具有重要意義。

近年來，涌現出很多對車架輕量化的方法。劉齊茂[1]采用有限元軟件ANSYS的零階方法對車架部件的截面尺寸進行優(yōu)化。向湘林、左孔天[2]提出自適應響應面法對貨車車架進行優(yōu)化。由于傳統(tǒng)的優(yōu)化方法容易陷入局部最優(yōu)解，因此，進化算法也有了很大的發(fā)展。在遺傳算法不斷改進的基礎上，田闊[3]運用改進的遺傳算法對車架結構進行了優(yōu)化。所使用的優(yōu)化方法逐漸由傳統(tǒng)的規(guī)劃方法向進化方法發(fā)展，努力替代以往靠經驗優(yōu)化和設計車架的手段。帝國競爭算法是由Atashpaz-Gargari 和Lucas[4]于2007年提出的一種政治社會進化算法，該算法借鑒于現實世界中帝國主義國家擴張和掠奪殖民地的歷史進程，通過大量殖民地向帝國的靠近，來尋找到全局最優(yōu)解，帝國之間的競爭促成了算法的收斂。不少學者也對此算法進行了改進[5-6]。本文通過帝國競爭算法對車架各個部件厚度進行優(yōu)化設計，構造新的輕型貨車車架結構，使車架部件受力更加合理，提高了材料利用率，節(jié)約了成本。在保證車架的各項基本性能[7-9]的情況下，實現了輕型貨車車架結構的輕量化設計。

1 帝國競爭算法

帝國競爭算法是最近幾年提出的高級啟發(fā)式最優(yōu)化算法。此算法的思想源于人類政治社會進化的過程，即歷史上帝國對殖民地的掠奪和帝國之間的競爭。

1.1 建立初始帝國

最優(yōu)化的目的是要尋求目標函數最優(yōu)解。在此，首先建立一個N維設計變量的數組表示國家。

計算每個國家的成本函數

每個國家的權力與其成本函數成反比例關系。成本低的前幾個國家成為帝國主義國家，其余國家成為殖民地。按照帝國主義國家權力的大小劃分殖民地。我們定義每個帝國主義國家的規(guī)范化成本為

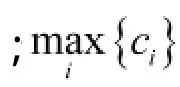
式中，Mimp為總的帝國數。分配給每個帝國的殖民地數量為

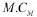
1.2 同化

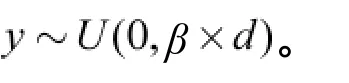
式中，{V}為有殖民地指向帝國的方向向量。

1.3 換帝

當殖民地向帝國靠近時，若有一個殖民地的成本低于帝國成本，在此情況下，該殖民地與帝國交換位置，原來的帝國成為殖民地，而成本小的殖民地成為新的帝國。

1.4 競爭

一個帝國的權力與該帝國的總成本大小成反比，帝國的總成本為

在競爭中，每個帝國都有可能占據最弱帝國中的最弱殖民地。為了衡量每個帝國的權力，首先將總成本規(guī)范化為

根據每個帝國的權力，形成權力向量P

創(chuàng)建一個與P相同大小的概率矩陣R

D中最大值相對應的帝國將獲得擁有權。該帝國會獲得最弱帝國中的最弱的殖民地。

1.5 合并

在不斷的競爭中，最弱的帝國會逐漸失去所有的殖民地。最后，該帝國會被其它帝國吞并而成為殖民地。

1.6 收斂

經過N年后，即迭代N次后，當僅剩一個帝國統(tǒng)領所有殖民地時，算法結束。

2 車架有限元分析

本文所研究的某輕型載貨汽車的車架為邊梁式，由2根縱梁和6根橫梁組成。汽車額定載重量為1 t，車架總長度為4.633 m，寬度為1.69 m，高度0.17 m。車架所選用的材料為Q235-A，許用屈服應力為235 MPa。車架有限元模型如圖1所示。

車架承受著來自發(fā)動機、駕駛室、駕乘人員、油箱、貨箱（滿載）等載荷，根據靜力等效原則[10]，將以上各個載荷施加在有限元模型相應接觸面的節(jié)點上。相應的載荷數據見表1，載荷施加位置如圖2所示。

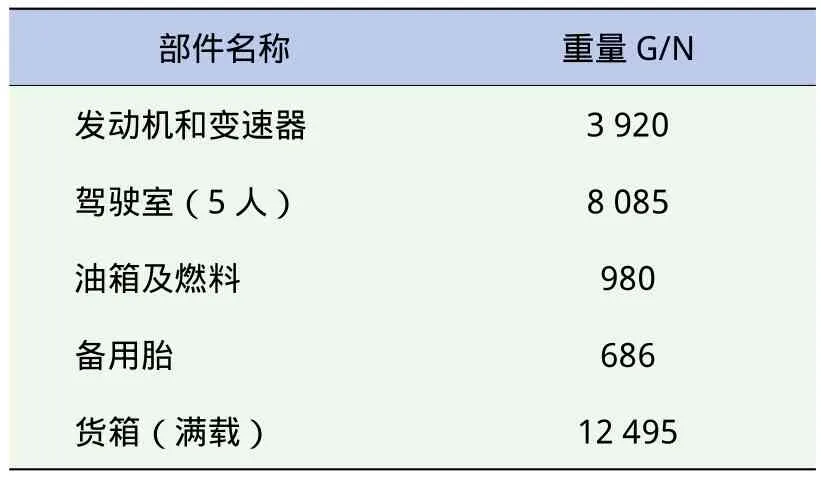
表1 車架所受載荷

2.1 彎曲工況

彎曲工況[11]是研究汽車滿載時承受靜載荷時車架的抗彎特性。這是檢驗車架剛度最主要的工況之一。利用有限元分析軟件對本文有限元模型進行分析計算，選取4個車輪的輪心為4個支撐點。車架彎曲工況邊界條件是約束4個車輪垂直方向的位移，約束右側兩個車輪的橫向位移，約束左前輪和右前輪的縱向位移。經分析計算彎曲工況應力分布云圖、位移分布云圖如圖3和圖4所示。最大應力出現在車架第2個橫梁與縱梁接觸處，為27.161 MPa；最大位移出現在車架的尾部，為0.77 mm。

2.2 扭轉工況

扭轉工況[12]是研究車滿載時承受扭轉載荷時車架的抗扭轉變形的特性，主要考察車架左右縱梁在固定載荷下的扭轉狀況，所受載荷與彎曲工況相同。利用有限元分析軟件對本文有限元模型進行分析計算，選取4個車輪的輪心為4個支撐點。車架扭轉工況邊界條件是約束左側兩個車輪和右前輪垂直方向的位移，約束左前輪和右前輪縱向位移，約束左側兩個車輪橫向位移，完全釋放右后輪的全部自由度。經分析計算扭轉工況應力分布云圖、位移分布云圖如圖5和圖6所示。最大應力出現在第4個橫梁與縱梁接觸處，為121.091 MPa；最大位移出現在第5個橫梁與縱梁接觸處，為12.228 mm。

3 基于帝國競爭算法的車架優(yōu)化

3.1 優(yōu)化參數設置

根據某輕型貨車車架確定將要優(yōu)化的縱梁和橫梁的數量和位置，然后對縱梁和橫梁的各個板厚尺寸進行優(yōu)化。各個部件的板厚列于表2中。設計變量[13-14]取值范圍均是2～6 mm，狀態(tài)變量是最大位移12.228 mm 和最大應力121.091 MPa，目標函數是輕型貨車車架的質量。帝國競爭算法的初始國家數量為200，其中帝國數量為3，殖民地數量為197，迭代次數為50。

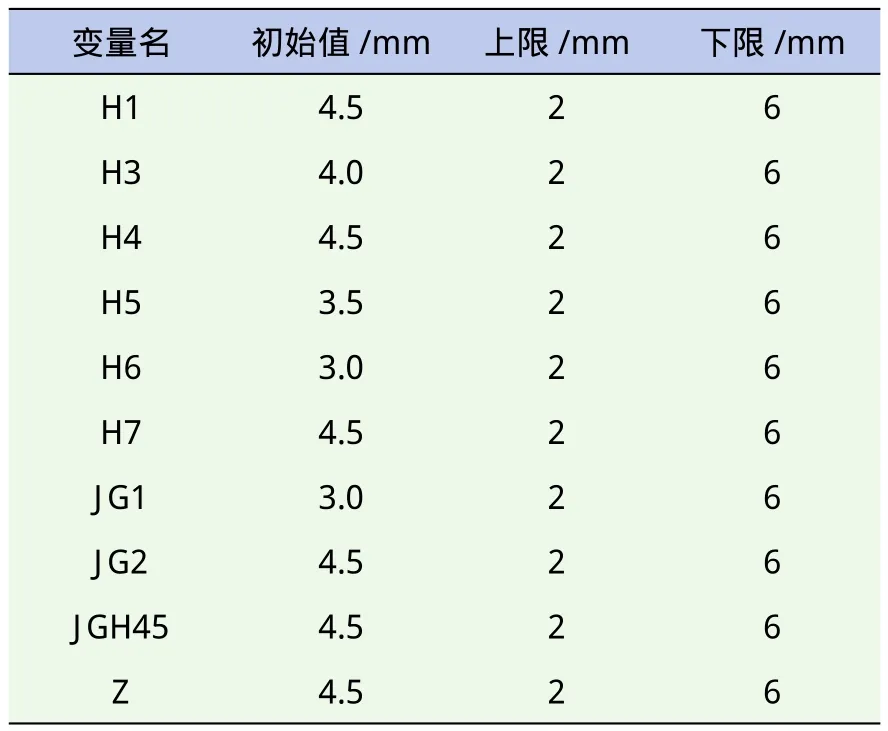
表2 車架各個板的厚度

3.2 車架優(yōu)化步驟

首先，根據表2生成若干組初始板厚，各自創(chuàng)建獨立的國家。計算各個國家的成本，即不同設計方案下的車架質量。然后選取質量最小的前Mimp個國家作為帝國，建立初始帝國。帝國建立之后，每個帝國中的殖民地向其帝國靠近，若發(fā)現某一殖民地的質量低于該帝國質量，交換二者位置。接著帝國之間進行競爭，消除權力小的帝國，直到剩下一個帝國而終止。此時該帝國即為最優(yōu)解。

車架優(yōu)化問題是一約束優(yōu)化問題，在初期生成若干組設計方案時，有些方案會不滿足結構設計的要求。因此，本文采用罰函數法處理約束條件，成本函數為

基于帝國競爭算法的車架優(yōu)化基本流程如圖7所示。

3.3 結果與分析

本文將帝國競爭算法的結果與有限元分析軟件ANSYS優(yōu)化算法中的零階算法[15]進行了比較，在設計變量的取值范圍和狀態(tài)變量相同的情況下，兩種算法得到的結果列于表3。

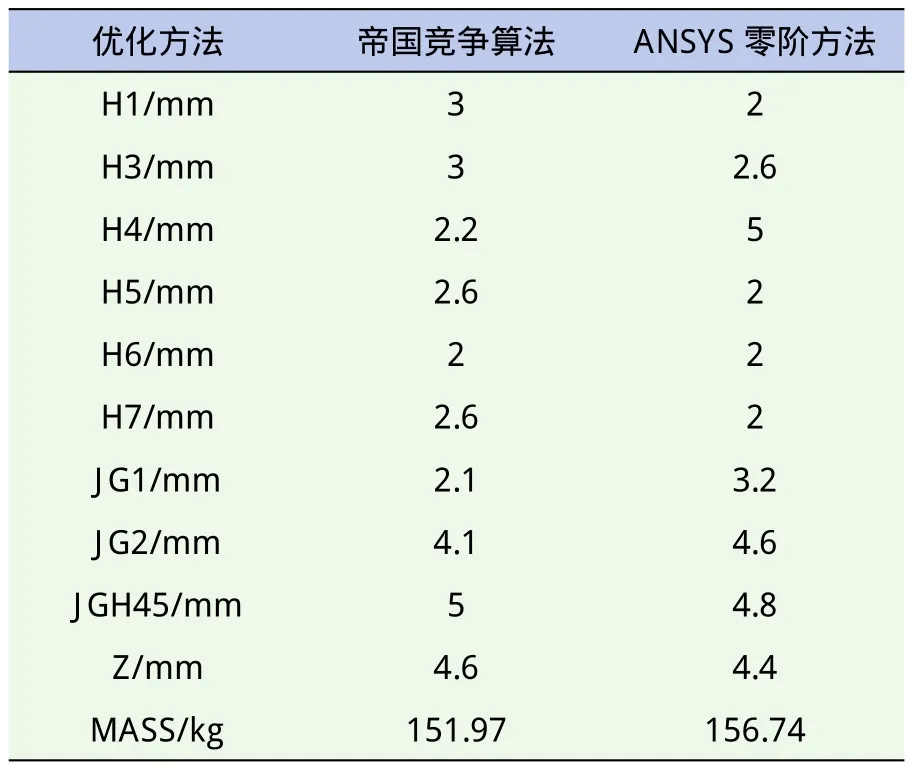
表3 兩種算法的結果比較

從表3中可以看出，通過優(yōu)化計算，有限元分析軟件ANSYS優(yōu)化算法中的零階算法將總質量減少了5.4%，帝國競爭算法計算總質量減少了8.3%，結果好于前者。說明帝國競爭算法具有較好的全局尋優(yōu)能力。

4 結論

本文在考慮某輕型貨車靜態(tài)時實際工況的基礎上，建立以最小化車架質量為目標函數的優(yōu)化模型。然后利用帝國競爭算法對車架主要部件的厚度進行優(yōu)化計算，以達到車架輕量化的目的。通過與ANSYS零階方法的對比，驗證了帝國競爭算法的適用性，體現了該算法更好的全局收斂能力。通過算例表明，帝國競爭算法能夠以較高的精度收斂到全局最優(yōu)點，體現了很好的實用價值和適用性。

References)

[1]劉齊茂. 汽車車架的結構優(yōu)化設計[J]. 機械設計與制造，2005，43(4)：1-3.Liu Qimao. Structure Optimization Design for the Automotive Frame[J]. Machinery Design & Manufacture，2005，43(4)：1-3. (in Chinese)

[2]向湘林，左孔天. 基于自適應響應面法的貨車車架優(yōu)化研究[C]. 第八屆中國CAE工程分析技術年會論文集，2012：90-94.Xiang Xianglin，Zuo Kongtian. Truck Frame Optimization Based on the Adaptive Responsive Surface Method[C].Proceedings of he 8th CAE Engineering Analysis Technology Annual Conference，2012：90-94. (in Chinese)

[3]田闊. 基于遺傳算法的車架結構優(yōu)化[D].天津：河北工業(yè)大學，2010.Tian Kuo. Frame Structure Optimization Based on Genetic Algorithm[D]. Tianjin：Heibei University of Technology，2010. (in Chinese)

[4]ATASHPAZ-GARGARI E，LUCAS C. Imperialist Competitive Algorithm：an Algorithm for Optimization Inspired by Imperialistic Competition[C]. IEEE Congress on Evolutionary Computation，Singapore，2007：4661-4667.

[5]ATASHPAZ-GARGARI E，HASHEMZADEH F.RAJABIOUN R，et al. Colonial Competitive Algorithm：a Novel Approach for PID Controller Design in MIMO Distillation Column Process[J]. Int J Intell Comput Cybernet，2008(3)1：337-55.

[6]KAVEH A，TALATAHARI S.Imperialist Competitive Algorithm for Engineering Design Problems[J]. Asian J Civil Eng，2010，11(6)：675-97.

[7]曲昌榮，郝玉蓮，戚洪濤. 汽車車架的有限元分析[J].輕型汽車技術，2008，36(9)：9-12.Qu Changrong，Hao Yulian，Qi Hongtao. Finite Element Analysis of the Vehicle Frame[J]. Light Vehicle Technology，2008，36(9)：9-12. (in Chinese)

[8]桂良進，周長路，范子杰. 某型載貨車車架結構輕量化設計[J]. 汽車工程，2003，25(4)：403-406.Gui Liangjin，Zhou Changlu，Fan Zijie. Lightweight Design for Frame Structure of a Heavy-Duty Truck[J]. Automotive Engineering，2003，25(4)：403-406. (in Chinese)

[9]歷輝，李萬瓊. 貨車車架的等效載荷簡化[J]. 汽車工程，1994，16(5)：310-314.Li Hui，Li Wanqiong. The Equivalent Load Determination of Truck Frame[J]. Automotive Engineering，1994，16(5)：310-314. (in Chinese)

[10]俆石安. 汽車構造-底盤工程[M]. 北京：清華大學出版社，2008.Xu Shian. Automobile Construction Chassis Engineering[M].Beijing：Tsinghua University Press，2008.(in Chinese)

[11]葉勤. 輕型載貨汽車車架有限元分析與優(yōu)化[D]. 武漢：武漢理工大學，2007.Ye Qin. Finite Element Analysis and Optimization of Light Truck's Frame[D]. Wuhan：Wuhan University of Technology，2007. (in Chinese)

[12]張旭. 某轎車車身有限元分析[J]. 農業(yè)裝備與車輛工程，2009，47(7)：26-28.Zhang Xu. Finite Element Analysis of a Car Body[J]. Agricultural Equipment & Vehicle Engineering，2009，47(7)：26-28. (in Chinese)

[13]張朝暉. ANSYS12.0 結構分析工程應用實例解析[M].北京：機械工業(yè)出版社，2010.Zhang Chaohui. Engineering Applications of ANSYS12.0 Structural Analysis[M]. Beijing：China Machine Press，2010. (in Chinese)

[14]曾攀，雷麗萍，方剛. 基于ANSYS平臺有限元分析手冊：結構的建模與分析[M]. 北京：機械工業(yè)出版社，2011.Zeng Pan，Lei Liping，Fang Gang. Finite Element Analysis Guide：Modeling and Analysis of Structure[M]. Beijing：China Machine Press，2011. (in Chinese)

[15]王虎奇. 基于ANSYS零階方法的裝載機前車架的結構優(yōu)化設計[J]. 今日科苑，2007，11(8)：114.Wang Huqi. Structural Optimizaion Design of the Front Frame of a Wheel Loader Based on the ANSYS Zero Order Method[J]. Today Panorama of Modern Sciences，2007，11(8)：114. (in Chinese)