有限采樣影響下秩減估計器的波達方向估計性能分析

王鼎，姚暉，吳瑛

（解放軍信息工程大學 信息系統工程學院，河南 鄭州450002）

1 引言

眾所周知，陣列誤差自校正方法需要將信源波達方向(DOA, direction-of-arrival)和陣列誤差參數根據某種準則進行聯合估計或聯合優化[1～3]，其中聯合估計所涉及到的高維、多模非線性優化問題往往會帶來龐大的運算量，從而使得算法的實時性和頑健性較差，全局收斂性也難以得到保證。為了克服陣列誤差自校正方法中存在上述問題，一類所謂“秩減估計器(RARE, rank reduction estimator)[4～16]”引起了國內外學者的廣泛關注，其主要優勢在于能夠實現陣列誤差參數和信源方位的聯合且“去耦合”估計，可避免迭代運算和局部收斂等問題。例如，文獻[4,5]分別針對均勻線陣和均勻圓陣互耦矩陣的特殊結構(Toeplitz結構)，提出了互耦自校正RARE；文獻[6～11]分別針對L字型陣、Y字型陣、十字型陣、均勻六邊形陣和圓環陣的互耦矩陣特性，提出了相應的互耦自校正 RARE；文獻[12]提出了累量域互耦自校正 RARE；文獻[13]利用精確校正的輔助陣元提出了一種可用于校正“方位依賴”幅相誤差的RARE，該方法也稱為輔助陣元法(ISM，instrumental sensors method)；文獻[14,15]提出了多子陣部分陣列誤差的自校正RARE，其中的陣列誤差包括子陣與子陣之間的陣元位置誤差或幅相誤差等；文獻[16]則提出了多子陣互耦自校正RARE等。上述一系列RARE都能夠在一定條件下取得較好的效果，并且能夠有效避免陣列誤差自校正方法中的一些缺點。

根據文獻[4～16]中的討論可知，RARE可以看成是 MUSIC算法[17]的一種推廣，或者說 MUSIC算法是RARE在沒有陣列誤差條件下的一種特殊形式。由于MUSIC算法是一種最為重要的DOA估計算法，所以關于其方位估計性能的理論研究報道相對較多，例如，文獻[18,19]利用一階誤差分析方法推導了有限采樣影響下MUSIC算法的方位估計均方誤差；文獻[20,21]利用二階誤差分析方法推導了有限采樣影響下MUSIC算法的方位估計偏置等。由于RARE是MUSIC算法的一種推廣，鑒于其在陣列誤差自校正方法中的重要性，筆者已在文獻[22～24]中從不同方面推導了其性能，其中包括未預期模型誤差影響下 RARE的角度分辨性能[22]和DOA估計性能[23]，以及有限采樣影響下RARE的角度分辨性能[24]。為了保證研究工作的系統性和完整性，本文將從理論上分析有限采樣影響下RARE的DOA估計性能。與文獻[22～24]中的分析方法不同的是，本文將基于文獻[25]給出的信號(或噪聲)子空間正交投影矩陣的擾動定理，分別推導了RARE的方位估計均方誤差、偏置以及測向成功概率的理論表達式，并針對文獻[4,5]中的均勻陣列互耦自校正RARE和文獻[13]中的輔助陣元法給出數值實驗。

在討論主題前，這里先給出一些文中常用符號的定義：1)?表示矩陣的Kronecker積；2)vec(·)表示矩陣向量化算子；3) Nn(μ, C )表示均值(向量)為μ，方差(矩陣)為C的n維高斯分布，χ2(n,δ)表示自由度為n，非中心參數為δ的卡方分布；4)向量(或標量)x˙(θ)、x˙(θ)和 ˙x˙(θ)分別表示向量(或標量)x(θ)對θ求一階、二階和三階導數；5)o(ε)表示ε的高階無窮小，而 O (ε)表示ε的等價無窮小。

2 預備數學知識

為了描述文中理論推導，本節將引出若干預備命題，它們對于文中的理論分析起著重要的作用。

引理1[26]設實隨機變量 x ～ χ2(n,δ)，則其特征函數為

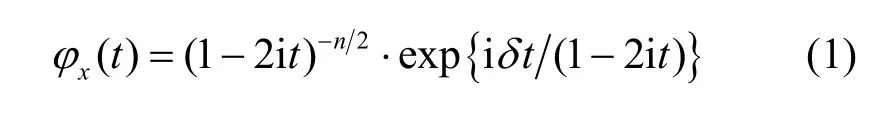
引理1的證明見文獻[26]。

命題 1 設n維實隨機向量 x ～ Nn( μ, In)，令A ∈ Rn×n為對稱矩陣，并且滿足rank[A] =m，假設A的m個非零特征值分別為 ρ1, ρ2,… ,ρm，相應的單位正交特征向量分別為 e1, e2,… ,em，則高斯隨機向量二次型 y =xTAx的特征函數為

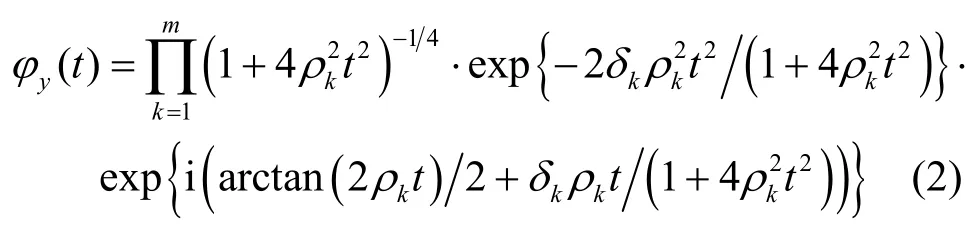
命題1的證明見附錄A。

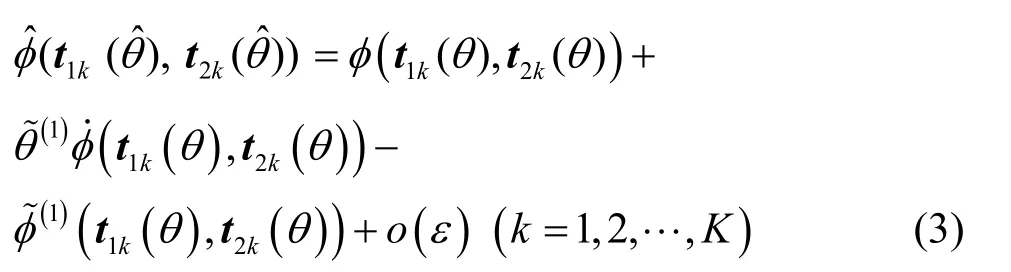
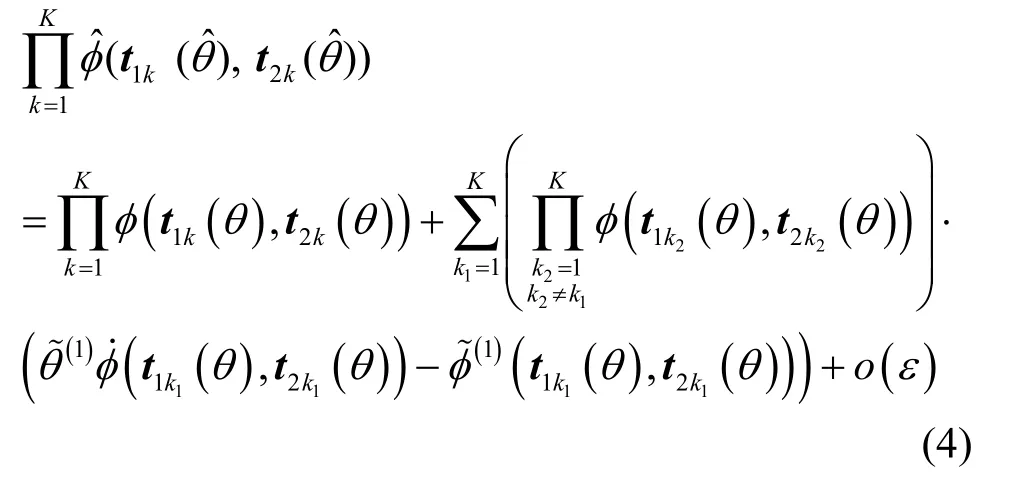
命題2的證明見附錄B。

進一步可得

命題3的證明見附錄C。

3 陣列信號模型和秩減估計器簡介

假設某陣列含有M個陣元，現在陣列遠場處有D個非相干的窄帶信源以平面波的方式入射，則陣列的輸出響應為

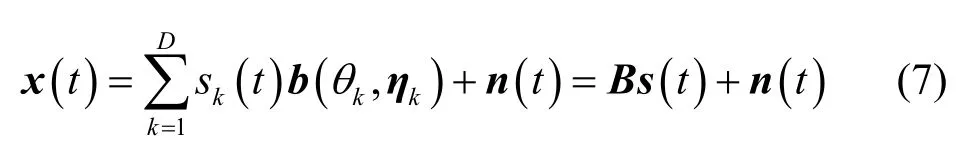
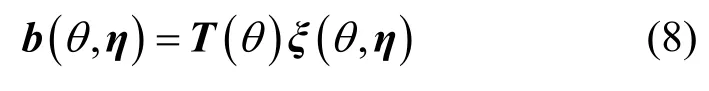
其中，T（θ）∈CM×K表示僅與方位θ有關的矩陣函數，這里將其按列分塊表示為 T （θ）=，而表示包含陣列誤差參數η的列向量。

根據式(7)可知陣列協方差陣為

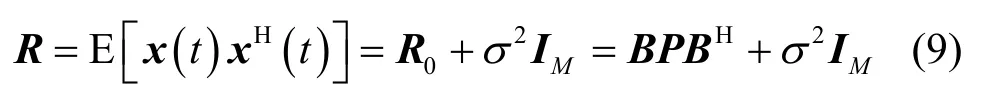
其中， R0=BPBH為無噪條件下的陣列協方差陣，為信源協方差陣(當信源統計獨立時，是對角矩陣；當信源統計相關但不相干時，是正定矩陣)，σ2表示噪聲功率。現對矩陣R進行特征分解，其特征值按照由大到小的順序可假設為[17]

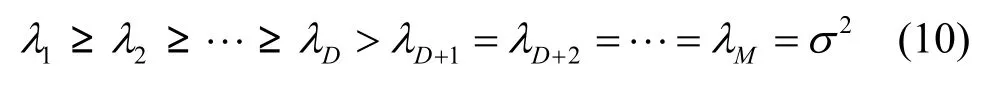
若令上述D個大特征值對應的單位正交特征向量分別為 u1,u2,… ,uD，并記 U = [ u1u2…uD]，則理想條件下信號子空間和噪聲子空間的正交投影矩陣分別為 Π = UUH和 Π⊥= IM-UUH，相應地RARE 空域譜為[4～16, 22～24]

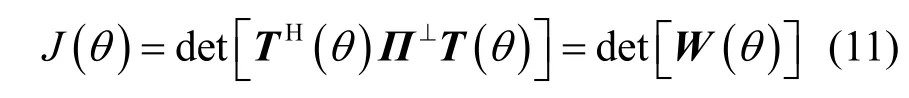
其中， W （θ ） = TH（θ） Π⊥T （ θ） ∈ CK×K。在參數滿足一定條件下[4～16]，信源方位可由下式精確獲得[4～16,22～24]

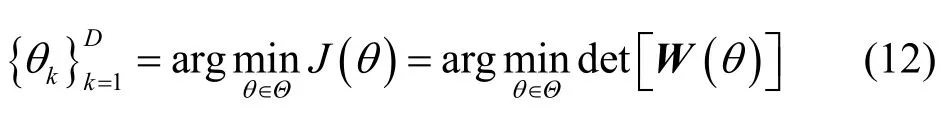
在實際計算中，由式(9)確定的理想協方差陣是無法得到的，只能通過有限采樣獲得它的一致(最大似然)估計值，其中N為樣本點數。若對R?進行特征分解，則仍可得到D個較大特征值，假設它們對應的單位正交特征向量分別為，并記，則有限采樣影響下信號子空間和噪聲子空間的正交投影矩陣分別為和，相對應的 RARE 空域譜為[4～16,22～24]

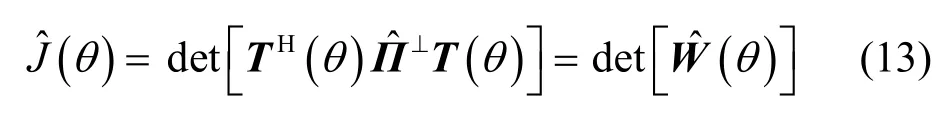
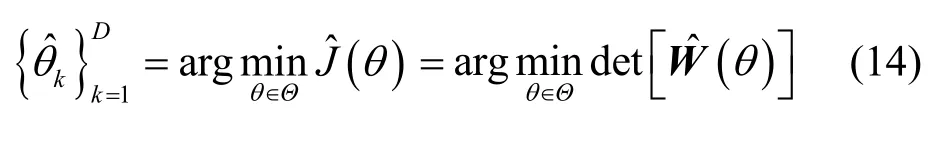
4 有限采樣影響下秩減估計器的方位估計性能分析

4.1 正交投影矩陣的擾動分析及其統計特性

定理1[25]設由矩陣特征分解得到信號子空間和噪聲子空間的正交投影矩陣分別為和，則有

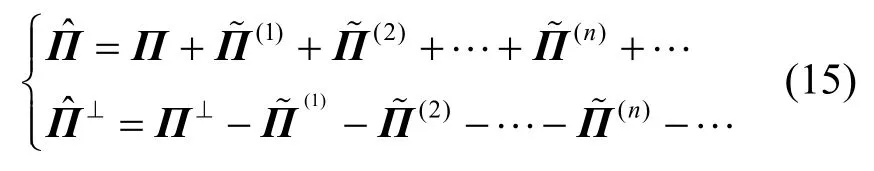
其中，

定理 1的證明見文獻[25]，它實質上給出了陣列協方差陣擾動量與信號(或噪聲)子空間正交投影矩陣擾動量之間的閉式關系，并且不難證明式(16)中的（n）是關于協方差陣擾動量的n次矩陣函數，因此也可以看成是n階擾動量，又因為，所以有為了對RARE的方位估計性能進行定量分析，本文首先基于定理1給出方位估計偏差與協方差陣擾動量之間的顯式關系。然而，方位估計偏差可由不同階數的誤差擾動量累加構成，當推導方位估計均方誤差時，通常采用一階誤差分析方法[18,19]得到方位估計偏差的一階擾動量，它可表示為而相應的均方誤差又可表示為但一階擾動量的均值為零，所以一階誤差分析方法難以獲得方位估計偏置的閉式表示。為了得到方位估計偏置的表達式，必須采用二階誤差分析方法[20,21]推導方位估計偏差的二階擾動量，它可表示為，而相應的偏置又可表示為

為了便于理論分析，這里需要給出關于正交投影矩陣一階和二階擾動量的統計特性。首先推導一階擾動量的二階統計特性，根據文獻[25]可知矩陣中的元素服從聯合漸近高斯分布，并且滿足

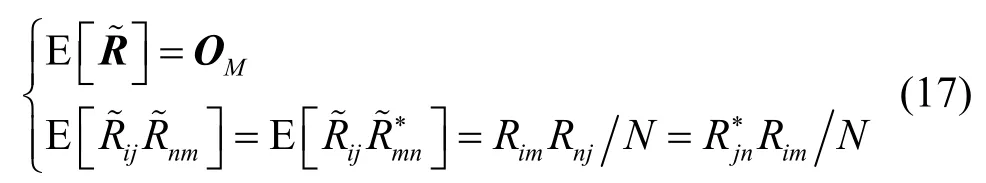
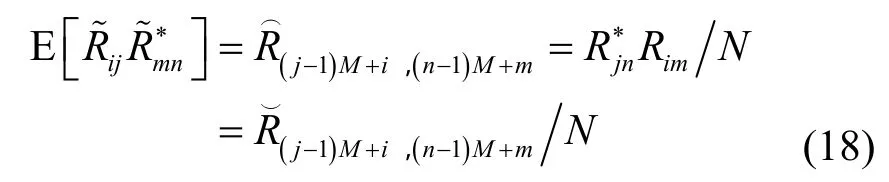
于是有

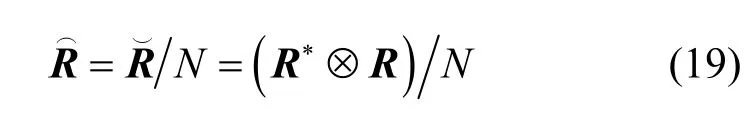
結合式(19)可知其二階統計量為

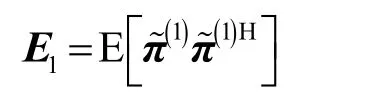
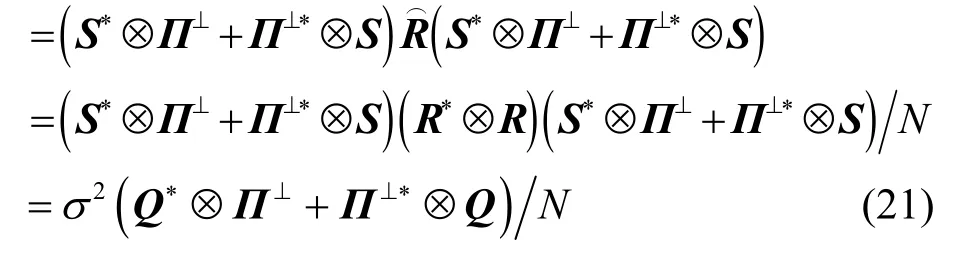
式(21)的成立還利用了性質 Π⊥R S =O 。M

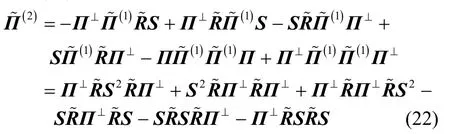
根據式(17)可得等式[25]

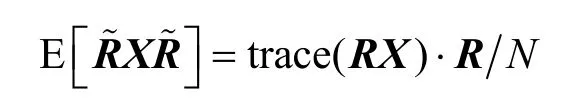
基于此可進一步得

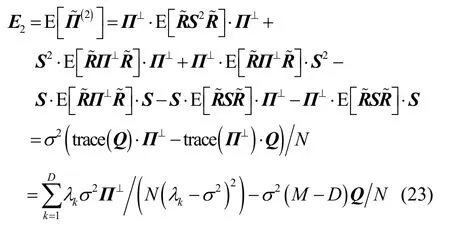
式(21)和式(23)分別對于推導 RARE的方位估計均方誤差和偏置起著重要作用。

4.2 秩減估計器的方位估計均方誤差

本節將推導RARE的方位估計均方誤差。記

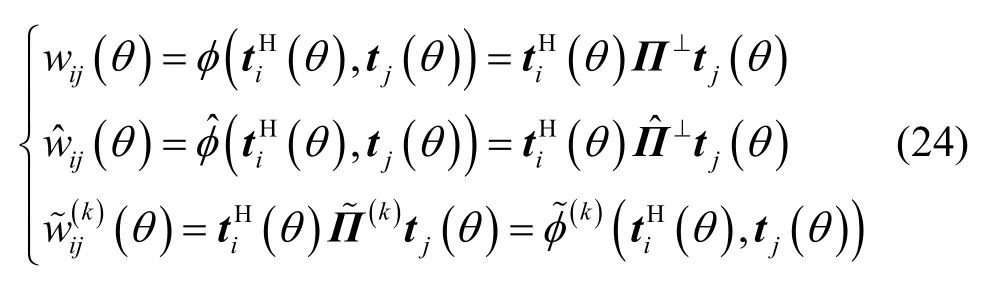
根據矩陣行列式的定義可知 RARE的空域譜為[22～24]

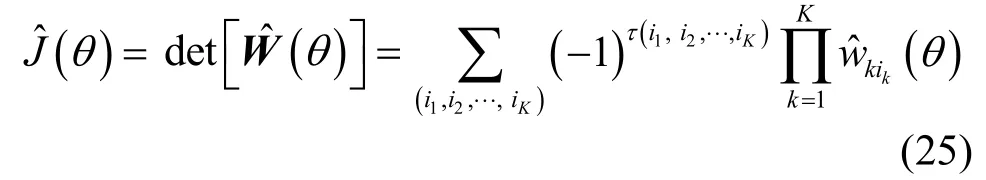
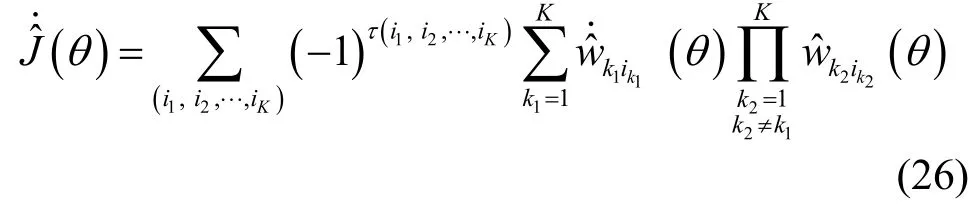
m

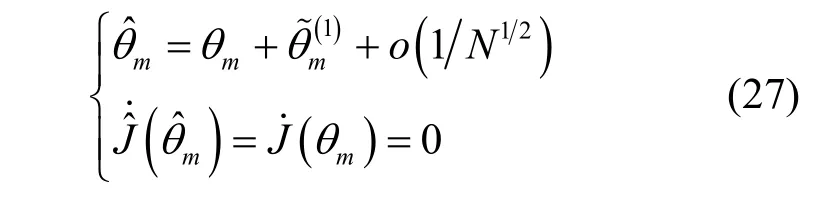
根據命題2可推得

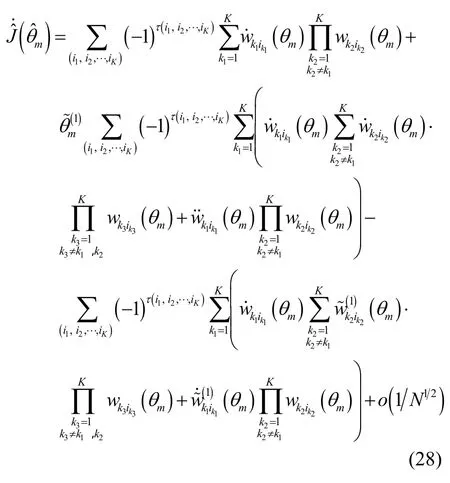
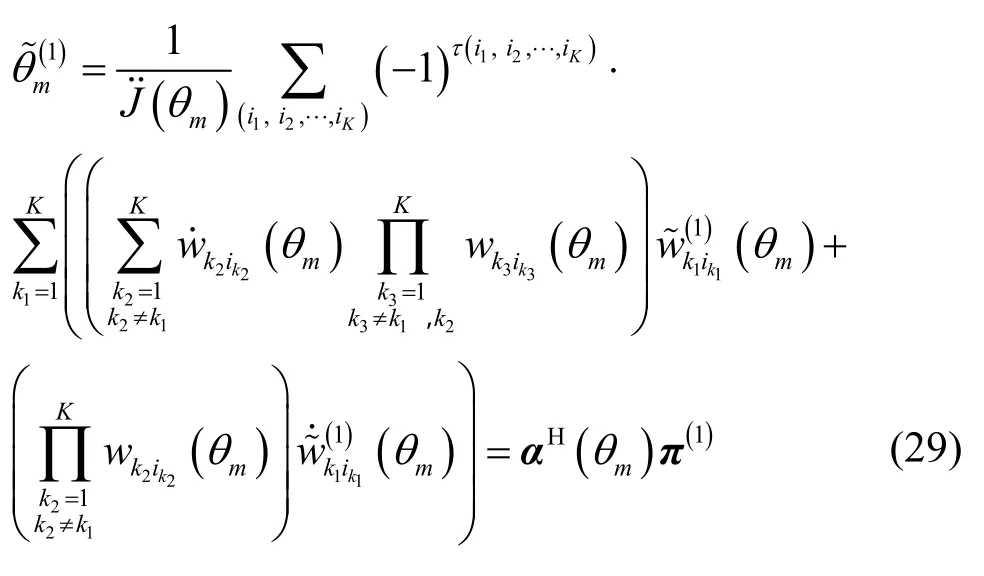
其中， α （ θ）= α1（θ）+ α2（θ） ， α1（θ） 和 α2（θ） 的表達式分別為

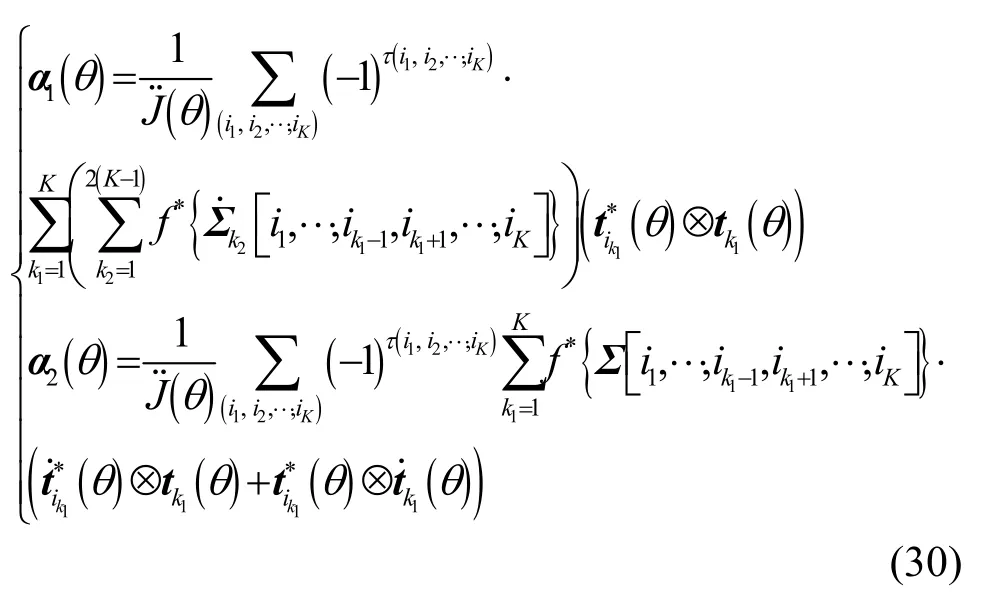
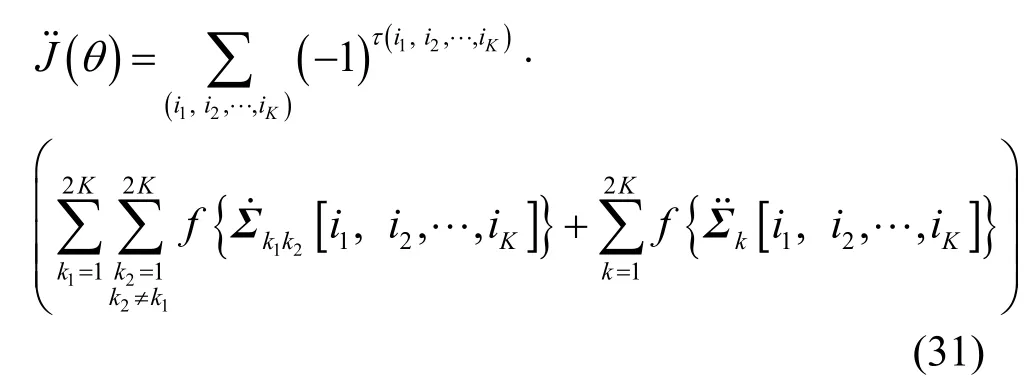
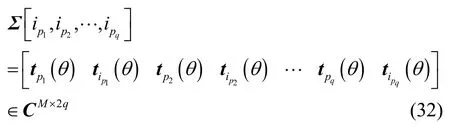
此外， ?｛·｝ 是滿足式(33)的標量函數：

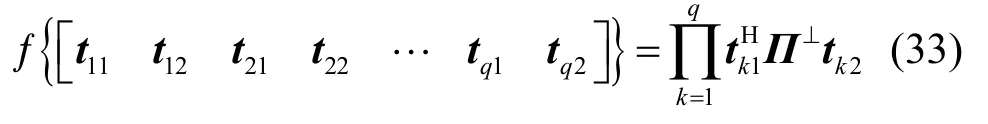
根據式(21)和式(29)可得第m個信源的方位估計均方誤差為

2）受凍部位。凍害大多以主干凍傷為主，主要在地面以上30～50 cm，最高可達100 cm，一般樹體受凍部位多在樹干西北方向，向南方向凍害輕或未受凍。徐香等品種嫁接口及以上部位受凍嚴重。

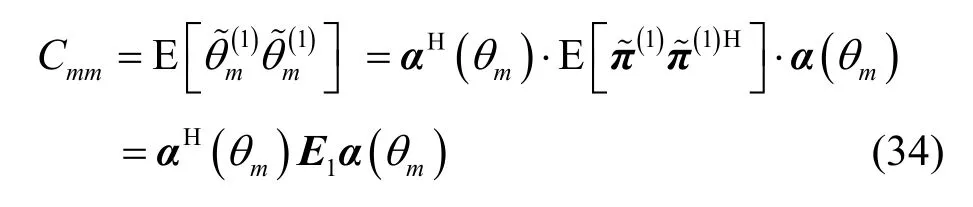
為了便于4.4節中推導RARE的整體測向成功概率，這里還需要給出RARE的方位估計方差陣，不妨記方位估計偏差的一階擾動向量為

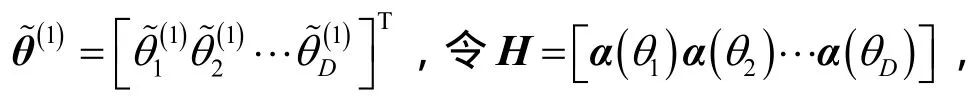
則可得RARE的方位估計方差陣為

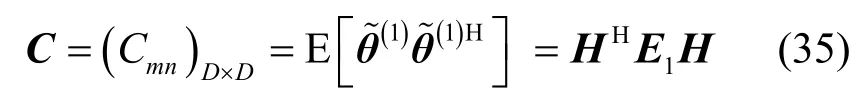
4.3 秩減估計器的方位估計偏置

本節將推導RARE的方位估計偏置。考慮第m個信源的方位估計，設是對應于真實方位θm的估計值，其二階擾動量為，則有

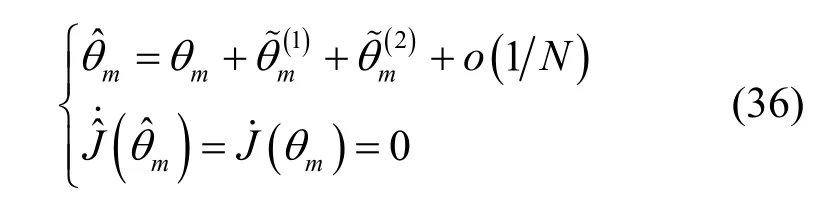
根據命題3和一些代數推導可得

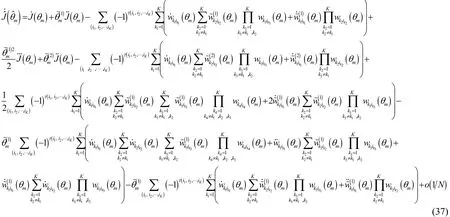
結合式(29)和式(36)可得

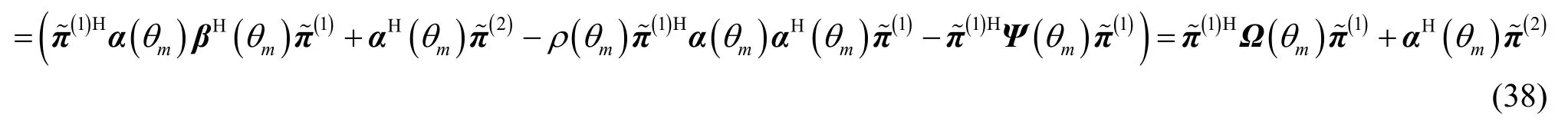
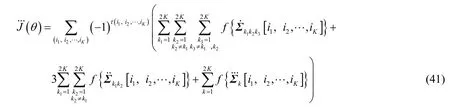
根據式(23)和式(38)可得第m個信源的方位估計偏置為

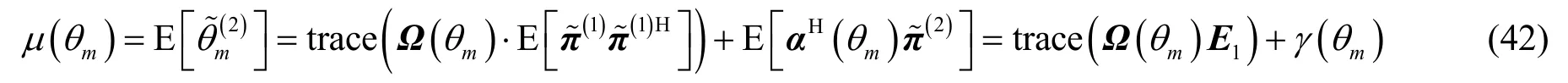
其中， γ（ θ） = γ1（θ） + γ2（θ） ，而 γ1（θ） 和γ2（θ） 的表達式分別為

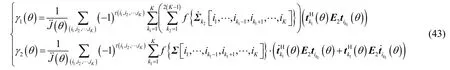
4.4 秩減估計器的測向成功概率

除了方位估計均方誤差和偏置外，測向成功概率也是超分辨率譜估計算法的一項重要性能指標，然而相關的理論研究報道并不多見，筆者曾在文獻[27]中推導了模型誤差影響下 MUSIC算法測向成功概率的計算公式，此外，還在文獻[23]中推導了未預期模型誤差影響下RARE的測向成功概率的計算公式，而本節則將基于文獻[23]和文獻[27]中的分析方法推導有限采樣影響下 RARE的測向成功概率。所不同的是，文獻[23]和文獻[27]中并未考慮方位估計偏置，而本文考慮了偏置的影響。

在推導RARE的測向成功概率之前，需要首先確定RARE方位估計偏差的分布特性，根據前面的討論可知其一階擾動量服從漸近高斯分布，但其二階擾動量的概率分布則很難嚴格推導。文獻[28,29]在推導高斯模型誤差影響下MUSIC算法的角度分辨概率和方位估計統計特性時，根據李雅普諾夫中心極限定理認為由模型誤差二次項構成的分量也近似服從高斯分布，因此MUSIC算法的空域譜及其方位估計偏差也可近似認為服從高斯分布。事實上，在有限采樣影響下，方位估計偏差的一階項仍占據主導地位，而二階項的討論可類似于文獻[28,29]中的分析方法，于是這里不妨將RARE的方位估計偏差也近似看作為服從漸近高斯分布，并且其方差陣為C (由一階誤差分析方法獲得)，而均值向量為μ (由二階誤差分析方法獲得)，即其方位估計偏差向量滿足需要指出的是，文獻[30]在推導有限采樣影響下 MUSIC算法的角度分辨概率時也曾做過類似的近似假設，于是能夠將角度分辨概率的計算轉化為高斯概率密度函數的積分運算，其中的仿真實驗也驗證了其合理性，而本文第5節的仿真實驗也將驗證上述高斯假設的有效性。本文在明確RARE方位估計偏差分布特性的基礎上，下面將采用文獻[23]和文獻[27]中給出的關于“測向成功”的定義方式，分別推導針對單個信源和針對整體的測向成功概率。

4.4.1 針對單個信源的測向成功概率

定義 1[23,27]對于第m個信源，若滿足條件則認為是“測向成功”。

定義 1中的Δθ表示角度誤差容限，根據前面的討論可近似認為于是第m個信源的測向成功概率為

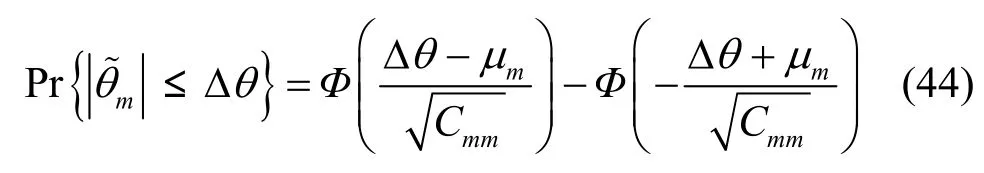
4.4.2 針對整體的測向成功概率

定義2[23,27]若滿足條件“則認為是“第一類整體測向成功”。

顯然，為了計算第一類整體測向成功概率需要明確D個信源方位估計偏差的聯合概率密度函數，根據前面的分析可知隨機向量的概率密度函數可近似表示為

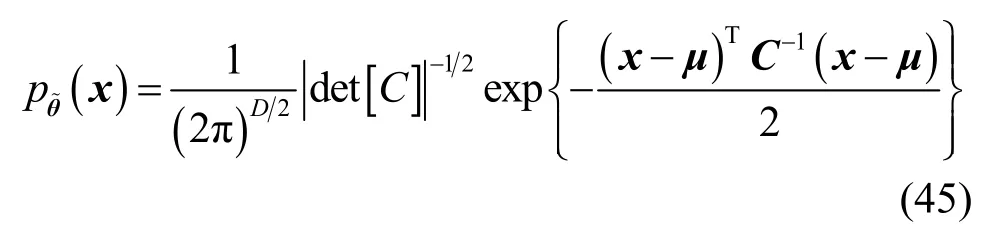
于是第一類整體測向成功概率為

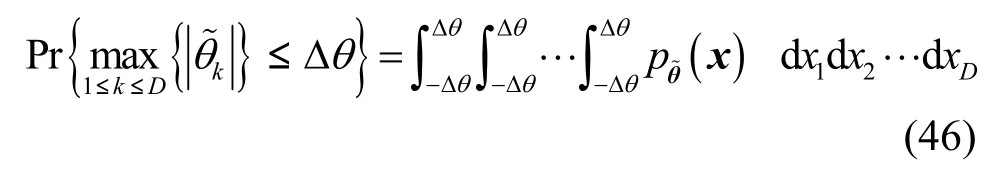
式(46)實質上是立方體上的高維積分問題，它可通過數值積分的方法獲得其數值解。

定義3[23,27]若滿足條件“則認為是“第二類整體測向成功”。

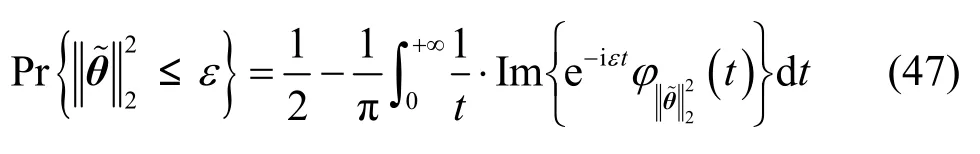
其中， ε = D （Δθ ）2，而是的特征函數，它是計算整體測向成功概率的關鍵。假設矩陣C的D個非零特征值分別為 ρ1, ρ2,… ,ρD，相應的單位正交特征向量分別為 e1, e2,… ,eD，則根據命題1可得

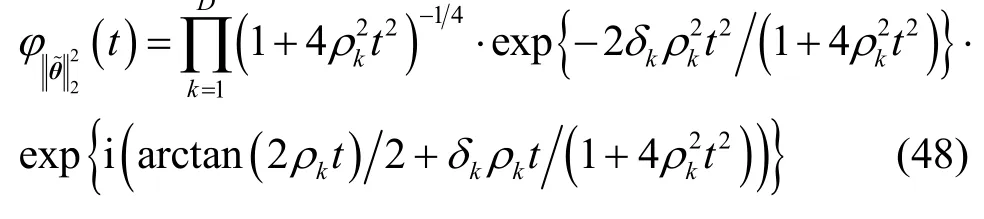
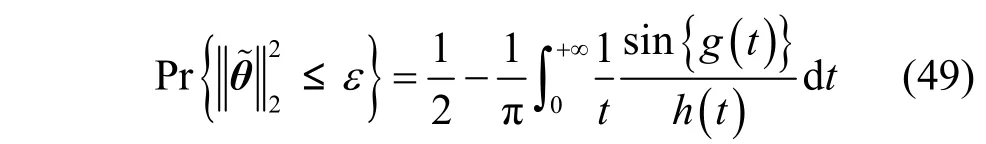
其中，

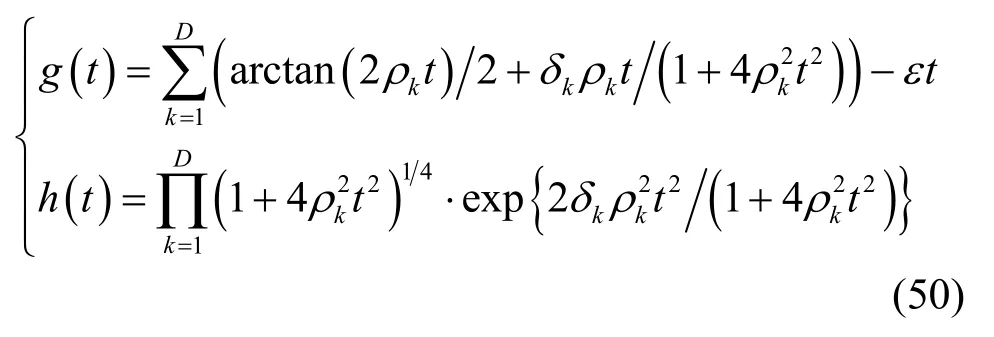
顯然，式(49)中的積分只能通過數值計算的方法獲得其數值解，為了計算該數值解，還需要考慮其中的積分函數在 t → 0 和t→+∞時的數值。首先根據洛必達法則容易驗證

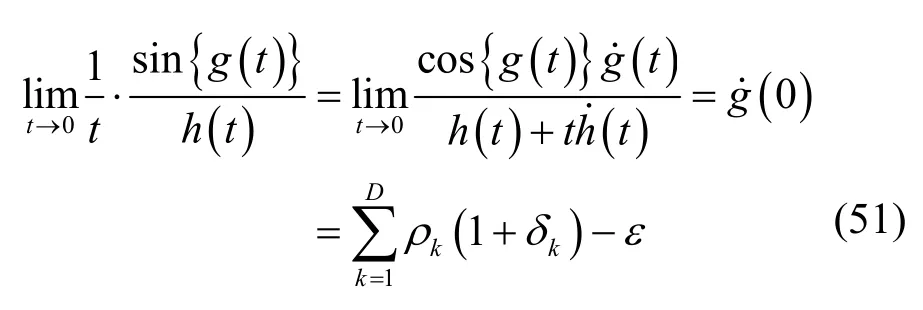
當t→+∞時，由于積分函數的分子有界，分母將按照遞增的方式趨于無窮大，因此該積分函數將以較快的速度趨于零，于是在進行數值計算時，只需要將積分上限設置為一個足夠大的正數即可。至此，可給出計算第二類整體測向成功概率的計算方法。

步驟 1 利用式(35)計算矩陣C，根據式(42)計算向量μ。

步驟3 根據特征向量計算標量因子δk=

步驟4 利用數值積分的方法計算式(49)。

至此，本節已經給出了針對單個信源的測向成功概率和兩類整體測向成功概率的計算方法，而根據文獻[23]和文獻[27]中的討論可知：1)第一類整體測向成功概率一定不大于單個信源的測向成功概率；2)第一類整體測向成功概率必然小于第二類整體測向成功概率，這些結論由它們的定義方式所決定。下面將通過一系列仿真實驗驗證文中理論推導的有效性。

5 數值實驗

這里先做以下幾點說明：1)下面是針對文獻[4,5]提出的均勻陣列互耦自校正RARE和文獻[13]提出的輔助陣元法給出的數值實驗；2)盡管 MUSIC算法也是一種特殊的RARE，但在下文的數值實驗中都同時給出了RARE和MUSIC算法的性能曲線，并且若不做特殊說明，下文的MUSIC算法是在不存在任何陣列誤差的條件下進行的；3)計算測向成功概率的誤差容限Δθ均設為0.5o；4)文中所有仿真圖中的連續曲線都是理論預測值，即根據文中的理論推導計算所得，而離散點都是仿真實驗值(2 000次Monte Carlo獨立實驗統計結果)。

5.1 針對僅存在單個信源的仿真實驗

本節將針對文獻[5]提出的均勻圓陣互耦自校正RARE給出數值實驗，假設陣列流型為八元均勻圓陣，并且相鄰3個陣元之間產生互耦效應，即文中的 3K= ，其互耦因子分別為1、0.12-0.18i和-0.05+0.06i，現僅有單個信源到達該陣列，信源方位為50o。首先，固定半徑波長比為1，圖1分別給出了RARE和MUSIC算法的方位估計均方根誤差、偏置以及測向成功概率隨著信噪比的變化曲線；接著，固定信噪比為10dB，圖2分別給出了RARE和MUSIC算法的方位估計均方根誤差、偏置以及測向成功概率隨著半徑波長比的變化曲線。

從圖1和圖2中可以得到如下結論：1)在上述數值實驗條件下，3種性能參數的理論值和仿真實驗值能夠較好地吻合，從而驗證了文中理論推導的有效性；2)無論RARE還是MUSIC算法，它們的方位估計精度都隨著信噪比和采樣點數的增大而提高；3)對于 MUSIC算法而言，其方位估計精度隨著半徑波長比的增大而提高，但對于RARE而言，其方位估計精度的變化規律則復雜得多，3種性能參數并不是簡單地關于半徑波長比的單調函數，在上述數值實驗條件下，當半徑波長比從0.8增至0.9時，RARE的性能會迅速下降，而當半徑波長比大于0.9時，RARE的性能又會迅速提高，這一特性由RARE復雜的空域譜函數所決定；4)在上述數值實驗條件下，MUSIC算法的方位估計偏置都接近于零，然而RARE卻并非如此，從圖1(b)中可以看出，當半徑波長比固定為 1時，若信噪比低于 12dB，RARE就會存在偏置，而從圖2(b)中可以看出，當信噪比固定10dB時，RARE會在半徑波長比取值范圍為0.8～1之間產生一定偏置；5)在上述數值實驗條件下，MUSIC算法的方位估計精度在絕大多數情況下優于RARE，但從圖2(a)中可以看出，當信噪比固定10dB且半徑波長比大于1.2時，RARE的方位估計均方誤差卻略小于MUSIC算法。

圖1 方位估計均方根誤差、方位估計偏置、測向成功概率隨信噪比的變化

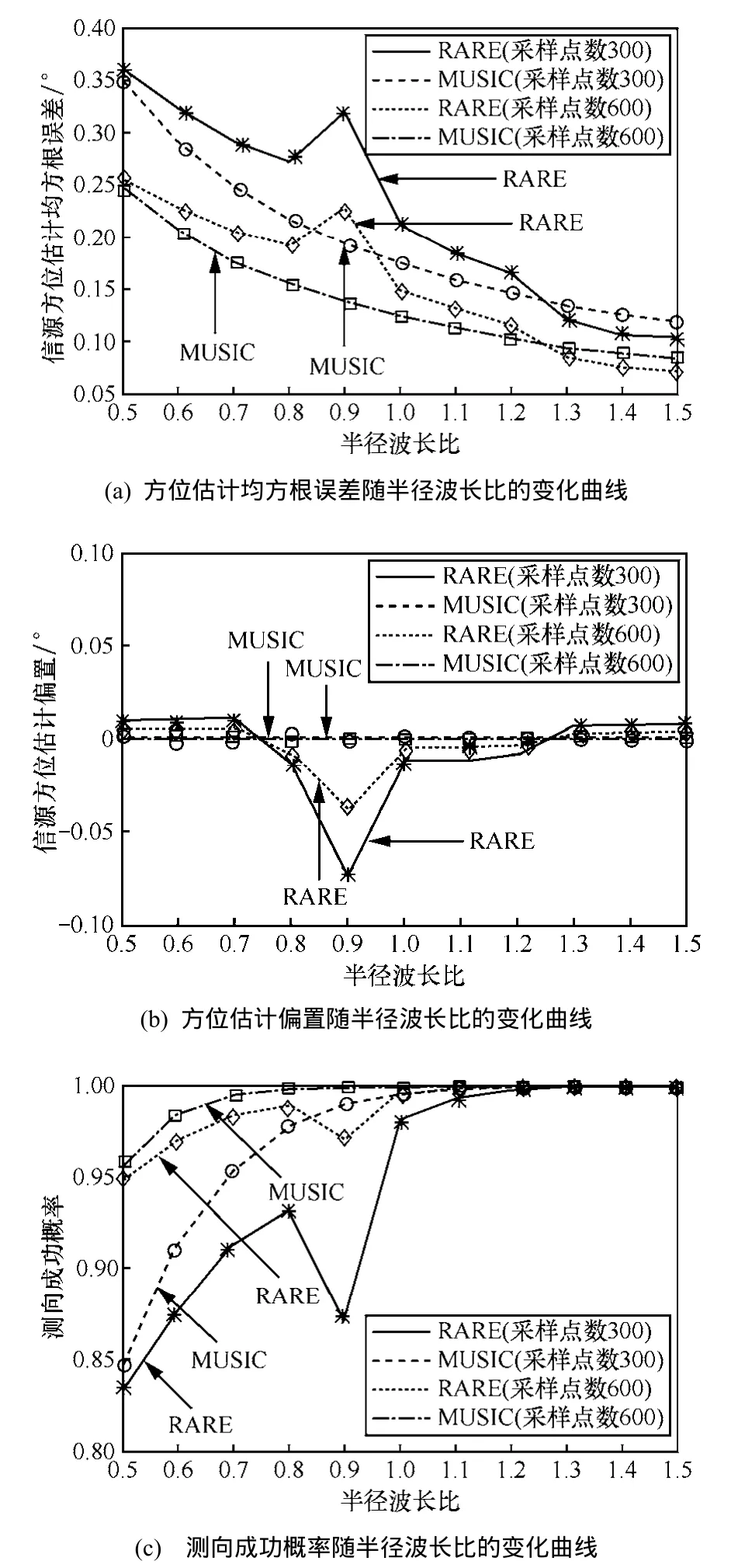
圖2 方位估計均方根誤差、方位估計偏置、測向成功概率隨半徑波長比的變化

這一結論似乎有悖于常理，但仔細分析則并非如此。正如本節開頭所指，文中的MUSIC算法是在沒有任何陣列誤差的條件下進行的，在此處就是指沒有互耦效應，因此RARE和MUSIC算法所處理的數據模型是不同的，所以在某些參數條件下RARE的方位估計均方誤差反而小于MUSIC算法是有可能出現的。事實上，若RARE與互耦存在的已知的MUSIC算法進行比較，則根據信息論原理可知前者的性能將始終低于后者，因為此時它們兩者所處理的數據模型是一樣的，這里不妨將RARE和互耦存在且已知的MUSIC算法進行比較，實驗條件同圖2(b)，并將采樣點數固定為300，表1給出了它們的方位估計均方根誤差的理論數值，從表中可以看出RARE的方位估計均方根誤差始終大于互耦存在的已知的MUSIC算法。

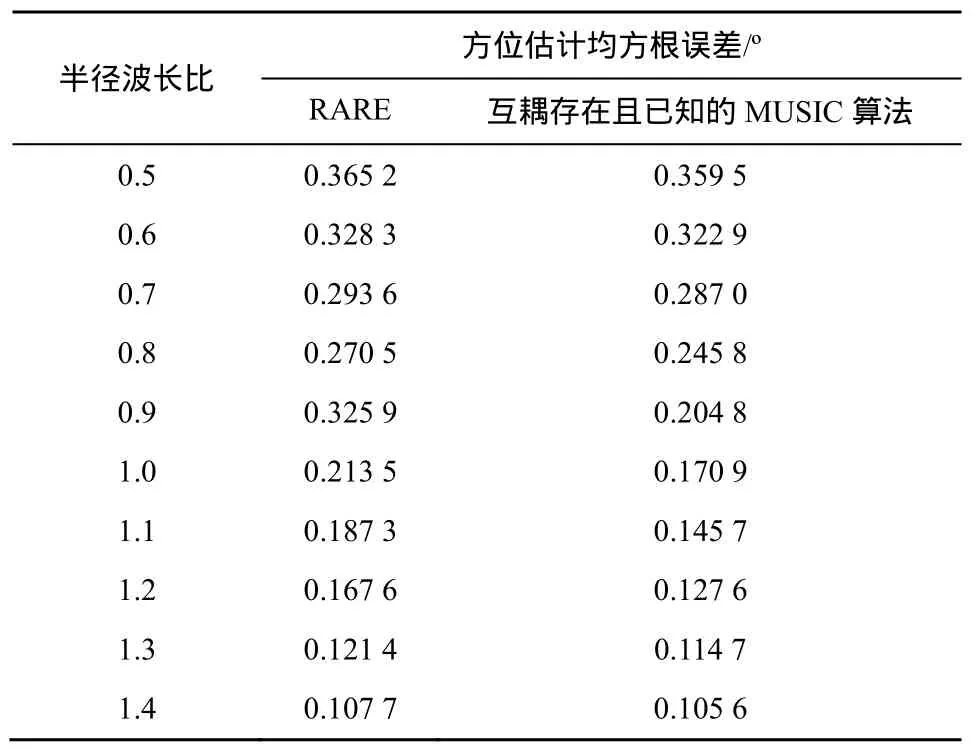
表1 方位估計均方根誤差的理論數值

5.2 針對存在2個信源的仿真實驗

本節首先針對文獻[4]提出的均勻線陣互耦自校正RARE給出數值實驗，假設陣列流型為九元均勻線陣，相鄰陣元間距與波長比為0.5，并且相鄰3個陣元之間產生互耦效應，其互耦因子同上，現有2個等功率相關但不相干信源到達該陣列，它們的相關系數為iπ6

0.1e ，信源方位(指與線陣夾角)分別為 64o和 82o，采樣點數為 500。圖 3分別給出了RARE和MUSIC算法的方位估計均方根誤差、偏置、針對單個信源的測向成功概率和整體測向成功概率隨著信噪比的變化曲線。

接著針對文獻[13]提出的輔助陣元法給出數值實驗，假設陣列流型為六元均勻線陣，相鄰陣元間距與波長比為0.5，其中前4個陣元為輔助陣元，即不存在任何幅相誤差，并且陣元的幅度因子均設為1，相位因子均設為0o，而后2個陣元存在方位依賴的幅相誤差，現有2個等功率相關但不相干信源到達該陣列，它們的相關系數為iπ60.1e ，信源方位(指與線陣夾角)分別為65o和85o，并且后2個陣元對應信源1的幅度因子為1.32和0.78，相位因子為28.7o和-23.8o，對應信源2的幅度因子為0.86和1.25，相位因子為-14.6o和16.5o，采樣點數仍設為500。圖4分別給出了RARE和MUSIC算法的方位估計均方根誤差、偏置、針對單個信源的測向成功概率和整體測向成功概率隨著信噪比的變化曲線。

圖3 方位估計均方根誤差、方位估計偏置、單信源的測向成功率、整體測向成功率隨信噪比的變化

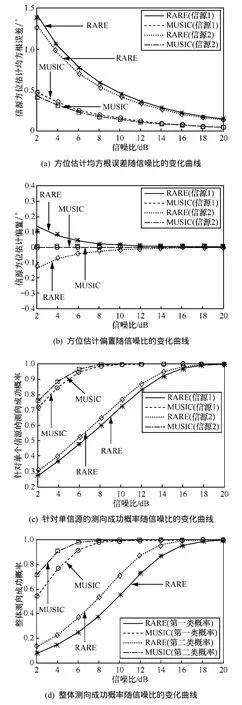
圖4 方位估計均方根誤差、方位估計偏置、單信源的測向成功率、整體測向成功率隨信噪比的變化曲線

從圖3和圖4中可以得到如下結論：1)在上述數值實驗條件下，3種性能參數的理論值和仿真實驗值仍能較好地吻合，從而進一步驗證了文中理論推導的有效性；2)無論是RARE還是MUSIC算法，它們的方位估計精度仍都隨著信噪比的增大而提高；3)在上述數值實驗條件下，MUSIC算法的方位估計精度始終優于 RARE；4)在上述數值實驗條件下，當信噪比較低時，RARE會產生一些偏置，然而MUSIC算法的偏置則仍基本接近于零，只是在圖3(b)中，當信噪比小于3dB時，MUSIC算法會有約 0.01o的偏置，事實上，無論是 RARE還是MUSIC算法，當參數條件往壞的方向發展時，它們都會逐漸產生偏置，只是相比而言，RARE更容易出現偏置；5)第一類整體測向成功概率始終不會高于單個信源的測向成功概率，并且第一類整體測向成功概率始終小于第二類整體測向成功概率，這一結論符合文獻[23]和文獻[27]中的分析結果。

最后，通過仿真實驗反映信源相關系數對RARE性能的影響，第1個實驗的仿真條件基本同圖3，只是固定信噪比為15dB，圖5給出了RARE的方位估計均方根誤差隨著信源相關系數幅度因子和相位因子的變化曲面。第2個實驗的仿真條件基本同圖 4，固定信噪比仍為 15dB，圖 6給出了RARE的方位估計均方根誤差隨著信源相關系數幅度因子和相位因子的變化曲面。

從圖5和圖6中不難看出：相關系數的相位因子對RARE性能的影響非常小，但相關系數的幅度因子對RARE的性能會產生一定影響，尤其當幅度因子大于0.8時，RARE的性能會迅速惡化，這是由于相關系數的幅度因子決定了兩信源之間的相關性，這一變化規律與MUSIC算法也是一致的(它們都是基于子空間技術提出的算法)。

6 結束語

本文從理論上定量分析了有限采樣影響下RARE的方位估計性能，基于文獻[25]中給出的信號(或噪聲)子空間正交投影矩陣的擾動定理，推導了RARE方位估計偏差的一階和二階擾動量，在此基礎上分別給出了其方位估計均方誤差、偏置以及測向成功概率的理論表達式。針對文獻[4,5]中的均勻陣列互耦自校正RARE和文獻[13]中的輔助陣元法給出了數值實驗，仿真結果驗證了理論推導的有效性。本文的結論對于RARE的工程應用具有一定指導意義。

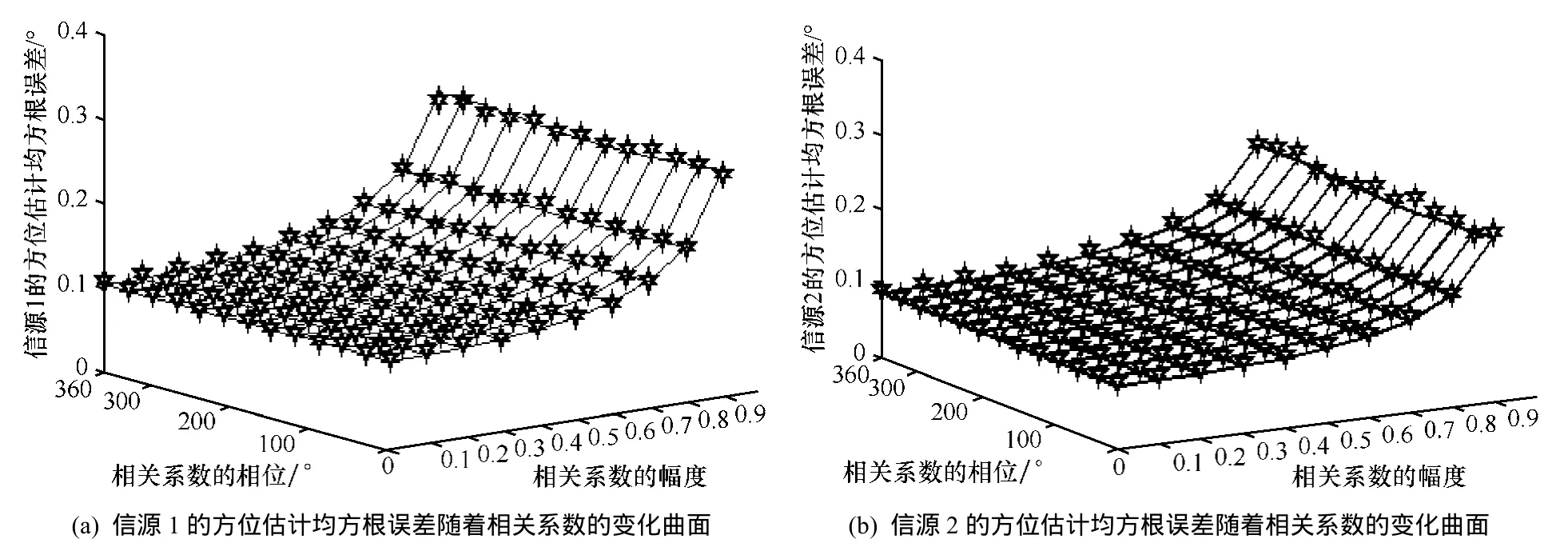
圖5 第1個實驗下，方位估計均方根誤差隨著相關系數的變化曲面

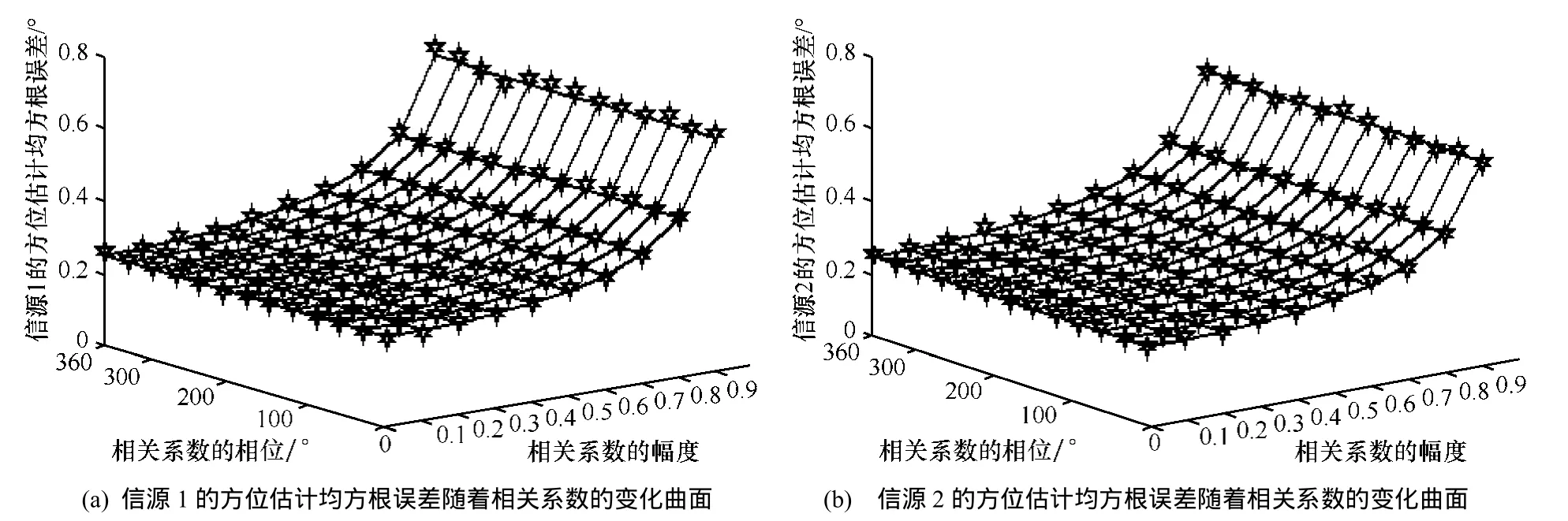
圖6 第2個實驗下，方位估計均方根誤差隨著相關系數的變化曲面

附錄A 對命題1的證明

附錄A將對命題1進行簡單證明。先對矩陣A進行特征分解可得，于是有

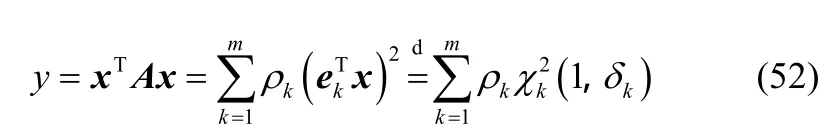
又因為相互獨立隨機變量和的特征函數等于各自特征函數的乘積，所以隨機變量y的特征函數可由式(2)確定。

附錄B 對命題2的證明

式(4)可通過數學歸納法進行證明，當 K = 2 時顯然成立，假設當 K = n -1時結論成立，則當K = n 時可得

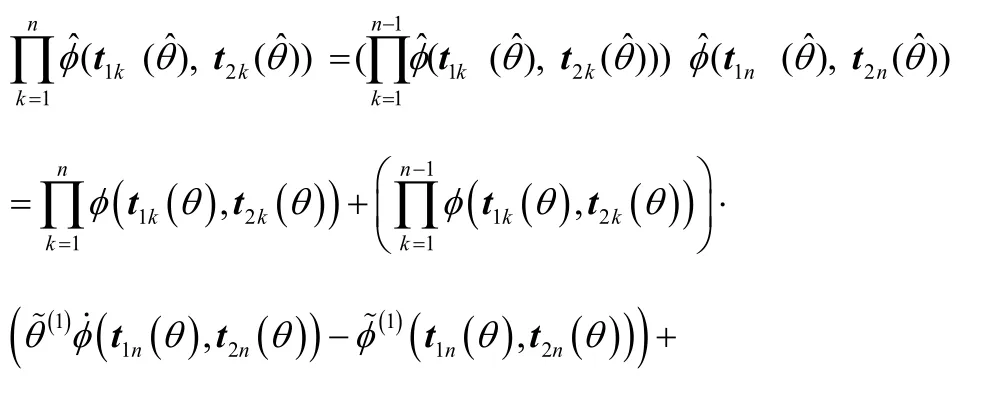
根據式(55)可知當K n= 時式(4)成立，因此命題2成立。

附錄C 對命題3的證明

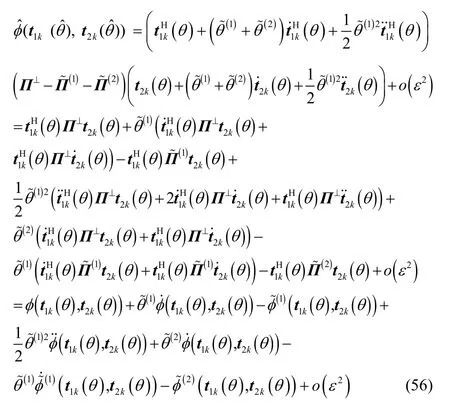
式(6)的證明過程類似于式(4)，可通過數學歸納法進行證明，鑒于篇幅考慮這里不再詳細描述。

[1] FRIEDLANDER B, WEISS A J. Direction finding in the presence of mutual coupling[J]. IEEE Transactions on Antennas and Propagation,1991, 39(3)：273-284.

[2] SELLONE F, SERRA A. A novel mutual coupling compensation algorithm for uniform and linear arrays[J]. IEEE Transactions on Signal Processing, 2007, 55(2)：560-573.

[3] WIJNHOLDS S J, VEEN A J. Multisource self-calibration for sensor arrays[J]. IEEE Transactions on Signal Processing, 2009, 57(9)： 3512-3522.

[4] WANG B H, WANG Y L, CHEN H. Robust DOA estimation and array calibration in the presence of mutual coupling for uniform linear array[J]. Science in China Series F： Information Sciences, 2004, 47(3)：348-361.

[5] QI C, WANG Y, ZHANG Y, et al. DOA estimation and self-calibration algorithm for uniform circular array[J]. Electronics Letters, 2005,41(20)：1092-1094.

[6] 吳彪, 陳輝, 楊春華. 基于L型陣列的方位估計及互耦自校正算法研究[J]. 電子學報, 2010, 38(6)：1316-1322.WU B, CHEN H, YANG C H. Study of DOA estimation and self-calibration algorithm for L-shaped array in the presence of mutual coupling[J]. Acta Electronica Sinica, 2010, 38(6):1316-1322.

[7] LIANG J L, ZENG X J, WANG W Y, et al. L-shaped array-based elevation and azimuth direction finding in the presence of mutual coupling[J]. Signal Processing, 2011, 91(5)：1319-1328.

[8] 吳彪, 陳輝, 胡曉琴. 基于Y型陣的互耦矩陣與DOA的同時估計方法[J]. 通信學報, 2010, 31(6)：119-126.WU B, CHEN H, HU X Q. Simultaneous estimation of mutual coupling matrix and DOA for Y-shaped array[J]. Journal on Communications, 2010, 31(6):119-126.

[9] HU X Q, CHEN H, WANG Y L, et al. A self-calibration algorithm for cross array in the presence of mutual coupling[J]. Science China Information Sciences, 2011, 54(4)：836-848.

[10] LIU C, YE Z F, ZHANG Y F. Autocalibration algorithm for mutual coupling of planar array[J]. Signal Processing, 2010, 90(3)：784-794.

[11] CHEN H, BAO Z. Performance analysis of self-calibration algorithm for concentric-UCA[A]. Proceedings of the International Conference on Wireless Communications and Signal Processing[C]. Suzhou, China, IEEE Press, 2010. 1-5.

[12] XIANG L, YE Z, XU X, et al. Direction of arrival estimation for uniform circular array based on fourth-order cumulants in the presence of unknown mutual coupling[J]. IET Microwaves, Antennas and Propagation, 2008, 2(3)：281-287.

[13] WANG B H, WANG Y L, CHEN H, GUO Y. Array calibration of angularly dependent gain and phase uncertainties with carry-on instrumental sensors[J]. Science in China Series F, 2004, 47(6)：777-792.

[14] PESAVENTO M, GERSHMAN A B, WONG K M. Direction finding in partly calibrated sensor arrays composed of multiple subarrays[J].IEEE Transactions on Signal Processing, 2002, 50(9)：2103-2115.

[15] SEE C M S, GERSHMAN A B. Direction-of-arrival estimation in partly calibrated subarray-based sensor arrays[J]. IEEE Transactions on Signal Processing, 2004, 52(2)：329-338.

[16] QI C Y, CHEN Z J, ZHANG Y S. DOA estimation and self-calibration algorithm for multiple subarrays in the presence of mutual coupling[A]. IEEE Proceedings on Radar, Sonar and Navigation[C]. 2006.333-337.

[17] SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986,34(3)：267-280.

[18] STOICA P, NEHORAI A. MUSIC, maximum likelihood, and Cramer-Rao bound[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1989, 37(5)：720-741.

[19] STOICA P, NEHORAI A. MUSIC, maximum likelihood, and Cramér-Rao bound：further results and comparisons[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1990, 38(12)：2140-2150.

[20] XIAO L X, BUCKLEY K M. Bias analysis of the MUSIC location estimator[J]. IEEE Transactions on Signal Processing, 1992,40(10)：2559-2569.

[21] LI F, LU Y. Unified bias analysis of subspace-based DOA estimation algorithms[J]. Control and Dynamic Systems, 1996, 77：149-192.

[22] 王鼎, 吳瑛. 未預期模型誤差影響下秩減估計空域譜的統計特性及分辨概率[J]. 應用科學學報, 2011, 29(2)：176-186.WANG D, WU Y. Statistical characteristics and resolution probability of rank reduction spatial spectrum in the presence of unexpected model errors[J]. Journal of Applied Sciences, 2011, 29(2):176-186.

[23] 王鼎, 吳瑛. 未預期模型誤差影響下秩減估計器的性能分析[J]. 通信學報, 2011, 32(8)：81-90.WANG D, WU Y. Performance analysis of rank reduction estimator in the presence of unexpected modeling errors[J]. Journal on Communications, 2011, 32(8):81-90.

[24] WANG D, WU Y. Effects of finite samples on the resolution performance of the rank reduction estimator[J]. Science China Information Sciences, 2013,56(1)：1-14.

[25] KRIM H, FORSTER P, PROAKIS J G. Operator approach to performance analysis of root-MUSIC and root-min-norm[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1992, 40(7)：1687-1696.

[26] 張潤楚. 多元統計分析[M]. 北京：科學出版社, 2006.32-33.ZHANG R C. Multivariate Statistical Analysis[M]. Beijing:Publishing House of Science, 2006.32-33.

[27] 王鼎, 吳瑛. 模型誤差條件下 MUSIC算法的測向成功概率[J]. 應用科學學報, 2010, 28(3)：289-296.WANG D, WU Y. Success probability of direction-finding of MUSIC algorithm with modeling errors[J]. Journal of Applied Sciences, 2010,28(3):289-296.

[28] FERRéOL A, LARZABAL P, VIBERG M. Statistical analysis of the MUSIC algorithm in the presence of modeling errors, taking into account the resolution probability[J]. IEEE Transactions on Signal Processing, 2010, 58(8)：4156-4166.

[29] FERRéOL A, LARZABAL P, VIBERG M. On the resolution probability of MUSIC in presence of modeling errors[J]. IEEE Transactions on Signal Processing, 2008, 56(5)：1945-1953.

[30] HARRY B, MICHAEL S W. Statistical characterization of the MUSIC null spectrum[J]. IEEE Transactions on Signal Processing, 1991,39(6)：1333-1347.

[31] DUGINA T N, MARTYNOV G V. Computing the distribution function of the ratio of quadratic forms in normal variables[J]. Journal of Mathematical Sciences, 1991, 53(6)：628-631.