基于kriging的給水管網節點壓力插值研究
邰明明
(重慶大學城市建設與環境工程學院,重慶市 400045)
1 引言
供水管網是市政設施的重要組成部分,及時并準確的掌握其運行狀態對供水管網的優化調度、管網的漏損檢測等具有重大意義[1]。隨著計算機技術的迅速發展,我國的自來水公司正在逐步建立供水管網的SCADA系統及配套的水力模型用于模擬穩態及延時狀態下管網的水力狀態[2]。但是 由于經濟技術等原因,布設的壓力監測點數量通常都遠少于管網的節點數[3],所以準確的掌握并模擬管網的水力狀態除了依賴于管網中有限的水壓或流量監測點外,采用有效的狀態估計方法也尤為重要。
目前,給水管網的狀態估計主要有兩類方法:微觀法與宏觀法。微觀法[4]是以管網水力分析理論為基礎,通過直接求解質量守恒與能量守恒方程得到整個管網的工作狀況,具有直觀性。但由于求解方程時采用基于統計平均的參數,而忽略了節點流量、管道內徑、紊流狀態下管道水損系數等的隨機性,得到的管網模擬值與實際值會存在一定偏差。宏觀分析方法是一種基于統計的分析方法。宏觀模型避開配水系統結構的復雜性,僅考慮系統中的幾個主要輸入輸出變量,在這些變量運行記錄的基礎上,采用回歸分析法建模[5],對管網中的特定節點進行狀態預測。
因此,將地統計分析方法引入給水管網節點壓力狀態推求中,利用kriging估計進行管網節點壓力插值分析,并根據管網節點內在關系,提出了地統計分析中相對距離的計算方法,獲得較好的分析結果。
2 給水管網節點壓力kriging插值估計原理
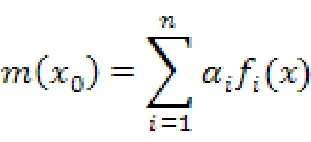

為了在滿足無偏估計的條件下得到最優估計,使估計值方差最小:

由
[6于],兩則點方之程間為的:協方差無法求得,引入變差函
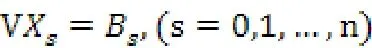
其中:
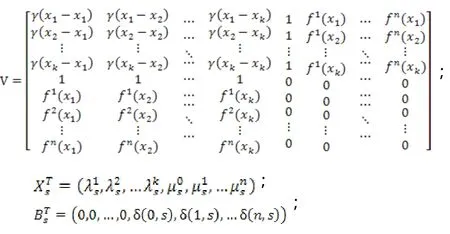
3 計算實例
上圖為一已知虛擬給水管網。各個節點實際流量未知,為了便于進行參照比較,設其各個節點某時段實際流量如圖所示,且其與設計流量不同。進行管網模擬得到各個節點壓力值作為估計結果的參照。
3.1采用kriging進行插值計算
已知編號為[1,7,13,17,20]的節點壓力,各點壓力為[82.15,56.81,36.49,41.35,17.80];
對已知點按照距離大小進行排序,假設協方差函數的變異函數,并回歸協方差變異函數系數,本例中采用球狀模型;
由于節點實際流量未知,所以需要根據實測管網總用水量,按面積比流量法進行流量分配,管網中總流量為338L/s,節點分配流量各個節點均為16.9L/s。以管網分配流量,設計管長、管徑、管道摩擦系數為已知條件,求得相對距離矩陣,矩陣第i行第j列元素表示節點i和節點j之間的相對距離。
4 結果與比較
管網模擬節點壓力值與估計值進行比較如下表:
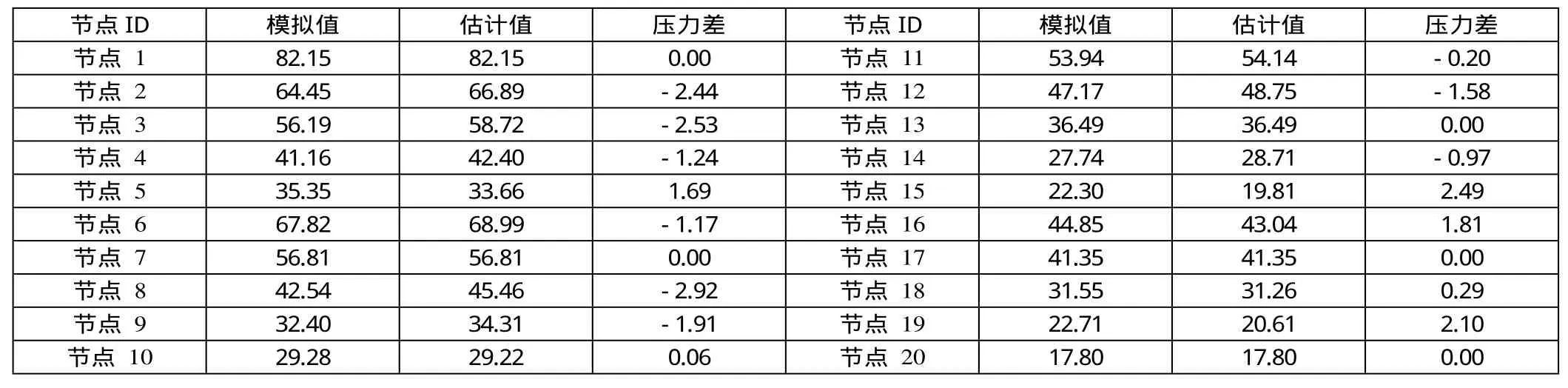
節點ID 模擬值 估計值 壓力差 節點ID 模擬值 估計值 壓力差節點 1 82.15 82.15 0.00 節點 11 53.94 54.14 -0.20節點 2 64.45 66.89 -2.44 節點 12 47.17 48.75 -1.58節點 3 56.19 58.72 -2.53 節點 13 36.49 36.49 0.00節點 4 41.16 42.40 -1.24 節點 14 27.74 28.71 -0.97節點 5 35.35 33.66 1.69 節點 15 22.30 19.81 2.49節點 6 67.82 68.99 -1.17 節點 16 44.85 43.04 1.81節點 7 56.81 56.81 0.00 節點 17 41.35 41.35 0.00節點 8 42.54 45.46 -2.92 節點 18 31.55 31.26 0.29節點 9 32.40 34.31 -1.91 節點 19 22.71 20.61 2.10節點 10 29.28 29.22 0.06 節點 20 17.80 17.80 0.00
從給水管網的最后估計結果來看,其與模擬值存最大-2.92m水柱的差距,分析其原因有以下幾點:(1)進行協方差估計的變異函數采用球狀模型,球狀模型的系數需要經過大量的實測值來進行估計,本例中只用5個已知點進行估計,稍顯不足,存在誤差;(2)可以嘗試采用更合適的變異函數模型。
5 結論與討論
該方法盡管存在一定估計誤差,但是對運行中管網通過有限的測壓點來估計整個管網所有節點的壓力值提供了一種思路;對管網各種水力性質采用插值方法估計準確性低的原因,對插值法在管網中應用的后續發展有指導作用。
[1]白健生.天津市供水管網的漏失現狀及分析[J].中國給水排水,2001.17(2):25- 27
[2]黃廷林,曹梅花.基于SCADA系統給水管網實時檢測爆管位置方法的研究[J].給水排水, 2007:33(5)
[3]HUANG Ting lin,CONG Hai bin,etc.Optimal state estimation of water distribution networks: application to Xi’an city[J] Xi’an Univ.of Arch.& Tech.(Natural Science Edition), 2005.Vol.37.No.1
[4]Ormsbee L.E..Explicit pipe network calibration[J]. Water Resource Plann Manage. 1986,112,2: 166–182
[5]Lansey K E, Shorbagy W.E., et al. Calibration assessment and data collection for water distribution networks[J].Hydraul Eng, 2001,127(4): 270- 279
[6]Pan Guocheng.地質統計學中結構分析的理論與方法[J].李鐘山,陳永良,譯.地質世界,1997,16 (3) :70 - 82

