加窗分數時延濾波器精度比較

張錦中 張中山

中國電子科技集團公司第三十八研究所，安徽 合肥 230088

引言

在很多數字信號處理應用中，對分數時延的需求越來越大。要實現固定的時延，數字信號處理技術比模擬技術更有優勢，且實現起來很容易，只需把信號在緩存器里存指定的時間就可以了。如果期望的延遲時間是采樣間隔的整數倍，這種方法是最優的；但是，當延遲值小于采樣間隔，特別是希望時延連續可調時，就需要更加復雜的方法。在符號時序恢復[1]，精確波束形成與預測語音編碼中，能過控制信號的采樣時刻，可以使系統性能得到一定的提升。為了得到兩個采樣之間的數據，在原理上，多速率方法通過插值、延時、重抽取可以實現，但對于自適應時延估計的動態場合，它就不適合了。對于多速率系統，通過標準的數字濾波器做精確的插值是更好的方法。

人們對分數時延濾波器的研究興趣主要集中在兩個方面，一個是只做分數時延（通過FIR與IIR濾波器實現[2]），另一個是把分數時延與其它功能一起設計（分數時延微分器）。文獻[3]對分數時延的研究進行了綜述；強大的最優化算法可以獲得極佳的分數時延，然而在實時數據通信領域，往往考慮采用較簡單的時延算法（通常使階數較少的FIR），簡單的方法可以快速調整到不同的時延值。要得到濾波器系數，通常使用閉式表達式，盡管它們的次最優性能部分地抵消了它們的實現優勢。本文的目的就是探討加窗方法對簡單分數時延濾波器的性能改善情況，特別是加Chebyshev窗時的時延精度進行了深入的研究。

1、分數間隔時延的FIR近似

首先，我們研究理想期望傳輸函數的近似方法。

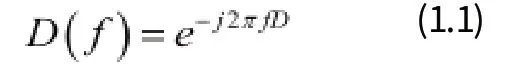
其中f是歸一化頻率，且

對于N個系數的FIR濾波器，a等于(N-1)/2，與線性相位濾波器設計相同。另一個時延因子d平移了濾波器沖激響應的對稱中心，且與傳統意義上的線性相位設計不同。事實上，即使d選為[-a,a]之間的整數，由于系數長度限定為N，對稱的系數丟棄一端的一些數據之后，系數也就不再對稱了。我們只對這樣的情況感興趣，當d是[-0.5,0.5]之間的小數，此時，濾波器系數會出現稍微的不對稱。

我們的任務就是設計一個z域傳輸函數H(z)使總的誤差

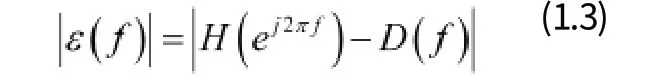
達到可接受的程度。對于任意的，在零頻，誤差要求可以很容易達到，但在Nyquist頻率處是不可能達到的。因此，我們只需關注95%帶寬的近似程度。全頻帶的高保真近似也是無意義的。時延濾波器沒有低通濾波器那樣的截止頻率。在研究過程中，我們只關注兩個方面的分數時延精度：f=[0,0.5](即半帶設計，占全頻帶的50%)與f=[0,0.9](即寬帶設計，占全頻帶的90%)。

如果帶限信號用離散時間信號表示，則固定時延可以用幅度與群時延分別為1與D的離散時間線性相位全通濾波器來近似。通過FOURIER變換，它的沖激響應可表示為

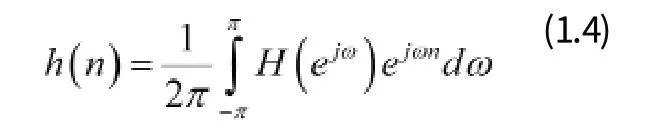
把式1代入式4得

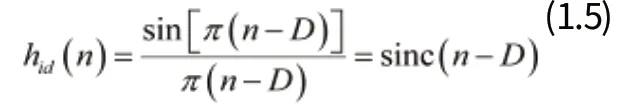
此沖激響應形狀與sinc函數相似，sinc函數定義為

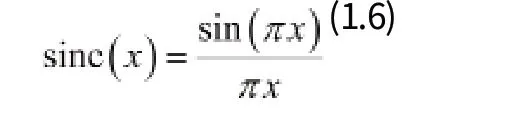
2、加窗SINC分數延時器

截斷SINC函數濾波器的性能太差，在實際中根本不能應用。降低Gibbs效應的常用方法就是進行時域加窗。加窗的濾波器沖激響應為：

其中，n是時間，取值范圍是0到N-1，h(n)是與H(ej2πf)對應的沖激響應序列。

精度評價標準是：

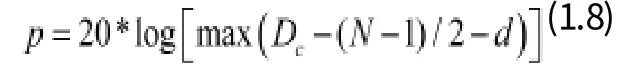
其中，Dc某個頻點的進延近似值，N是濾波器階數，d是期望的時延值。

使用升余弦窗與Chebyshev窗前后的SINC濾波器的時延精度性能如圖1所示：

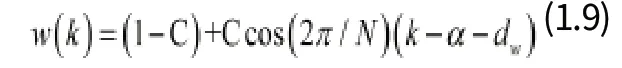
從圖中可看出von Hann窗(c=0.5)群時延特性要好于矩形窗，但CHebyshev窗的精度更好。圖1 的仿真條件是d=0.1，濾波器長度是17。

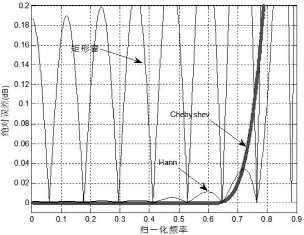
圖1 時延精度隨頻率的變化情況

圖2 寬帶時時延精度與濾波器階數的關系

寬帶時延精度與濾波器階數的關系如圖2所示，從圖中可以看出，Hann與Chebeyshev在階數為10左右時有一個拐點，當階進一步增大時，加Hann窗的精度隨數增大而減小；但加Chebeyshev窗時，精度并不是隨階數增大而減小，而是有一個最佳值，最佳值是65，相對Hann窗有40dB的好處；Chebeyshev窗的副瓣為-80dB。

半帶時延精度與濾波器階數的關系如圖3所示，此時精度的低階數拐點消失，加Chebeyshev窗的精度隨階數迅速提高，當階數為13時，就達到了最佳點，相對Hann窗有40dB的好處，同樣精度下Hann需要133階。

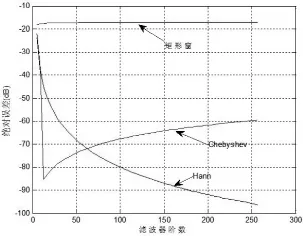
圖3 半帶時時延精度與濾波器階數的關系

時延精度與Chebeyshev窗主副比的關系如圖4與圖5所示，主副比越大，時延精度越高，主副比每增加20dB，時延精度也會提高20dB左右，但要達到最佳點，濾波器階數也要相應增加。半帶時，階數小于20就可以達到很高的時延精度。

圖4 寬帶時延精度與Chebeyshev窗主副比的關系

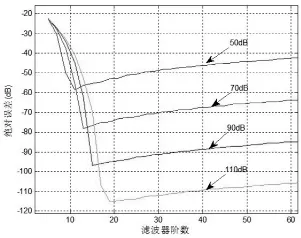
圖5 半帶時延精度與Chebeyshev窗主副比的關系

3、結語

分數階時延可以使用FIR濾波器來近似，加窗FIR濾波器是比較簡單有效的設計方法。本文研究了加窗分數時延濾波器的時延精度，對加Chebyshev窗的時延精度進行了深入研究，加Chebyshev窗的時延精度與窗的主副比有關，主副比越大，時延精度越高，需要的濾波器階數越高，并不是濾波器階數越高，精度越高，而是主副比一定時，濾波器階數有一個最佳值。

[1]Erup,L.,F.M.Gardner and R.A.Harris,"Interpolation in digital modems -Part II:implementation and performance",IEEE Trans.Comms.,vol.41,no.6,pp.998-1008,June 1993.

[2]Cain,G.D.,N.P.Murphy and A.Tarczynski,"Evaluation of several variable FIRfractional-sample delay filters",Proc.ICASSP94,Adelaide,Australia,vol.3,pp.621-624,19-22 April 1994.

[3]Timo I.LAAKSO,Splitting the unit delay !FIR all pass filters design,IEEE Signal processing magazine,January,1996.