剖析等價無窮小代換求解極限運算
楊春芝
(鐵嶺市師范高等專科學校,遼寧 鐵嶺 112001)
無窮小在數學理論研究上和實際工程應用中都具有重要作用,特別是在極限運算中具有獨特的優勢。正確合理的運用等價無窮小代換,會給極限求解帶來極大的方便,甚至能夠完成諾必達法則不能完成的極限求解。
1 無窮小定義及常用等價無窮小總結
1.1 無窮小定義
設函數f(x)在x0的某一去心領域內有定義(或大于某一正數時有定義)。 如果對于任意給定的正數ε (不論它多么小),總存在正數δ(或正數X),使得對于適合不等式0<|x-x0|<δ(或|x|>X)的一切x,對應的函數值f(x)都滿足不等式|f(x)|<ε,那么稱函數f(x)當x→x0(或x→∞)時為無窮小。 記作(或f(x)=0)。
1.2 常用等價無窮小總結
通常所用的初等函數有這樣五類: 三角函數、 反三角函數、對數函數、冪函數、指數函數,復雜方程式的求解中也為這五類初等函數的組合運算。 以下列舉出這五類初等函數的無窮小代換:
在當x→0 時:
冪函數無窮小代換:(1+x)a-1~ax (a 可以取整數也可以取分數);
指數函數無窮小代換:ex~x+1,ax~lna×x+1;
對數無窮小代換:ln(1+x)~x,loga(1+x)~x/;lna;
差的無窮小代換:1-cosx~x2/2,x-sinx~x3/6,tanx-x~x3/3,xln (1+x)~x2/2,tanx-sinx ~x3/3,x-arctanx ~x3/3,arcsinx-x ~x3/6,arcsinx-arctanx~x3/2;前面兩個代換后為二次函數,后面代換為三次函數。 而且從代換的等價無窮小方程式來看,代換的方程式明顯比前面未代換的方程式簡單得多。
2 無窮小代換求極限運算與羅比達法則對比
使用洛必達法則進行求解極限運算, 是我們計算極限時的首選方式,而且在絕大多數情況下,確實也能夠獲得快而且準確的結果。 但在一些復雜的求解中,洛必達法則并不具有優勢,如帶有三角函數和反三角函數的加減運算,因為三角函數中sinx、cosx 的兩次導數就回到了本身。 現舉例說明無窮小代換求解極限運算與羅比達法則對比:

當然,這需要熟記一些等價無窮小。 需要注意的是,等價無窮小的運用往往不止一次,只要發現運用洛必達法則運算困難,則可以嘗試等價無窮小代換。
3 等價無窮小代換應注意問題
根據等價無窮小的定義, 當方程式的乘積因子為無窮小時,則可利用等價無窮小進行代換。 但如果方程式中有因子為無窮小,但為加減法運算,則需要考察代換的條件是否成立。
3.1 無窮小因子處于加減法運算中
但在求解中,正確采用等價無窮小代換,則會得到:

在求解中, 因為無窮小因子tanx 是作為乘積因子出現在方程式中。
3.2 在無窮小代換中需注意趨近的值
在進行無窮小代換中需確定的是:第一,必須是無窮小;第二,必須是等價無窮小之間才能進行替換。 見下例:
在本題中,如果將用代換,導致錯誤的結果為1。正確計算結果應當為:
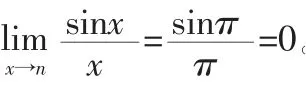
4 等價無窮小代換總結
(1)乘除運算中可以使用等價無窮小因子替換,加減運算中由于用等價無窮小替換是有條件的。 這時,滿足條件則可進行代換,不滿足可用泰勒公式、洛必達法則等方法來求極限。
(2)如果采用洛必達法則求導運算,在進行一次導數后,先觀察一下求導后的方程式能否進行等價無窮小替換,如果能替換,則進行替換。

