路面拋丸機高速軸的有限元分析

鄧孝龍 游小平 汪宗應(yīng)

(長沙理大工學(xué) 汽車與機械工程學(xué)院，湖南 長沙 410004)

水平移動式拋丸機是一種在歐美發(fā)達國家廣泛應(yīng)用的表面處理設(shè)備，目前隨著拋丸設(shè)備的不斷改進和技術(shù)成熟，拋丸工藝和設(shè)備已經(jīng)進入歐美發(fā)達國家公路養(yǎng)護、橋梁施工和機場維護等領(lǐng)域。中國在此方面的應(yīng)用卻很少，只有在少數(shù)項目中使用了拋丸工藝，而在高速公路、市政道路、機場跑道維護及混凝土橋梁防水涂裝方面還是一個空白。高速軸作為拋丸機的關(guān)鍵零件之一，高速軸受力情況是研究高速軸使用壽命的基礎(chǔ)，筆者結(jié)合ANSYS 軟件，建立高速軸的有限元模型并加以仿真分析，以期進一步明確高速軸的失效機理，為提高其使用壽命提供理論基礎(chǔ)。

1 高速軸的受力分析

高速軸是路面拋丸機需要設(shè)計的關(guān)鍵部件，它連接拋丸輪和帶輪。本文參照PW1255DA 型拋丸機的高速軸進行受力和有限元分析。圖1 為高速軸局部裝配示意圖。

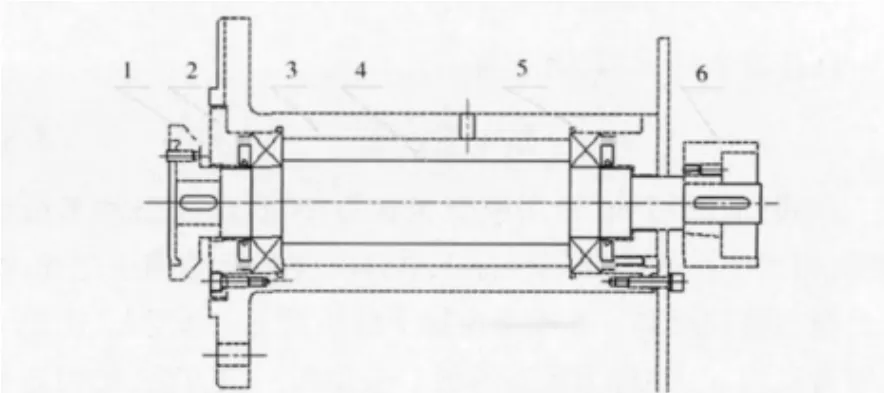
圖1 高速軸裝配示意圖

通過圖1 可以看到高速軸安裝在套筒內(nèi)，高速軸左端與連接盤連接(拋丸輪與連接盤連接)，右端與小帶輪連接，左端和右端均有一個滾動軸承作為支承。為了方便受力分析，根據(jù)圖1 的裝配示意圖將高速軸的受力情況簡化成為圖2 所示的受力分析簡圖。

圖2 高速軸受力分析簡圖

由電機輸出扭矩T 為:

其中P—表示電機功率，單位為kw

n—表示電機額定轉(zhuǎn)速，單位為r/min

依據(jù)選取電機的功率P=11kw，電機的額定轉(zhuǎn)速為2500r/min，則可以求出電機輸出扭矩的大小，即可知電機的輸出扭矩T 為42N·m，即可知受力圖中的扭矩，F(xiàn)1即為拋丸輪的重力G1，F(xiàn)2即為小帶輪的重力G2。

對左邊的鉸支座取力矩，則可得:

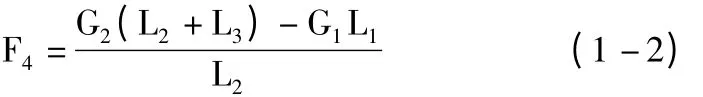
對右邊的鉸支座取力矩，則可得:

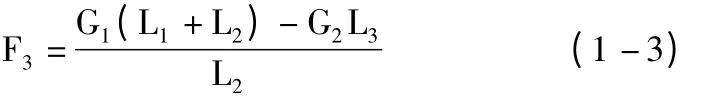
由于G1=80N、G2=20N 分別為拋丸輪和帶輪的重力，而L1=40mm、L2=181mm、L3=77mm，則可以分別計算出F3、F4。即

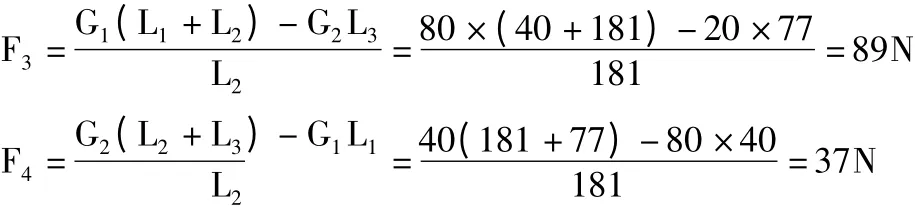
2 高速軸的靜力分析

2.1 三維模型的導(dǎo)入

高速軸并不是復(fù)雜的零件，根據(jù)材料力學(xué)的知識，應(yīng)力集中是引起軸破壞的主要原因之一，而應(yīng)力集中主要發(fā)生在軸的退刀槽、倒角等處。由于這些小結(jié)構(gòu)相對于高速軸的來說是很小的尺寸，直接在ANSYS 中建立模型，這些小結(jié)構(gòu)就會被忽略掉。高速軸的三維模型可用Pro/E 三維建模軟件建立，然后再導(dǎo)入到ANSYS 中進行分析計算。

2.2 單元選擇和材料屬性選擇

本文在有限元分析計算時選用的單元類型是SOLID95，這種單元類型是有20 個節(jié)點的三維實體單元，也就是說它由20個節(jié)點來定義，并且每個節(jié)點都有3 個自由度。而本文對高速軸的靜力分析中，施加在軸上面的載荷是彎扭的結(jié)合;在研究動力學(xué)時，更多的是具有交變應(yīng)力影響。所以選擇SOLID95單元能夠滿足高速軸靜力分析和動力分析的需要。高速軸的材質(zhì)為40Cr，它的性能參數(shù)為:彈性模量為E =206GPa，在20C0時的泊松比為μ=0.26 -0.3。

2.3 網(wǎng)格的劃分

由于高速軸具有比較好的對稱結(jié)構(gòu)，這為網(wǎng)格劃分帶來了很大的便利，可采用1 級的精度對其進行了網(wǎng)格劃分，這樣不僅提高數(shù)據(jù)的精度，也讓我們得到比較好的網(wǎng)格。經(jīng)過選擇處理，高速軸網(wǎng)格劃分后得到的模型圖3 所示。

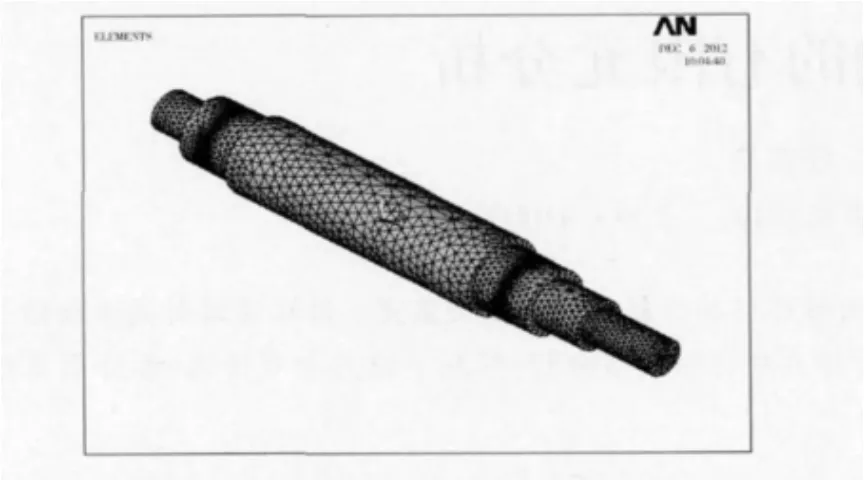
圖3 網(wǎng)格劃分后的高速軸模型

2.4 邊界條件設(shè)置及載荷施加

先設(shè)置好約束，第一個約束是安裝軸承處限制軸的軸向移動，因為在裝配時就是通過軸肩的定位來限制軸的軸向移動的，限制了軸的X 方向固定不動;第二個約束是限制軸承處的Y、Z 方向，因為軸承的固定作用使得軸在這兩個方向無法移動。高速軸主要受以下兩個力，一個是傳遞扭矩受到的扭矩力，這個力主要是通過平鍵傳遞的，所以受力的部位是在鍵槽處;同時高速軸會受到拋丸輪的壓力和帶輪的壓力，這兩部分壓力就是拋丸輪和帶輪的重力。

2.5 計算求解及分析結(jié)果

通過邊界條件設(shè)置和載荷的施加后，得到高速軸在靜力的條件下所受的應(yīng)力情況，圖4 為分析后得到的高速軸所受應(yīng)力分布圖。

圖4 高速軸應(yīng)力分布圖

通過應(yīng)力分布云圖，可以看到高速軸所受的所有應(yīng)力，也可清晰的發(fā)現(xiàn)高速軸最大應(yīng)力的發(fā)生部位，這樣就可以方便對應(yīng)力較大處進行改進，避免應(yīng)力集中。

通過上圖我們可以得到如下參數(shù)(如表1)。

表1 應(yīng)力參數(shù)圖

由于高速軸的材料是40Cr，而通過資料查找可以知道該材料的許用應(yīng)力為［σ］=560Mp，所以可以知道該軸設(shè)計是能滿足應(yīng)力強度要求的。

3 高速軸的模態(tài)分析

3.1 模態(tài)分析理論

模態(tài)分析就是計算線性結(jié)構(gòu)的自振頻率及振型，在結(jié)構(gòu)動力學(xué)問題中結(jié)構(gòu)固有頻率和固有振型是動力學(xué)問題分析的基礎(chǔ)。結(jié)構(gòu)模態(tài)是由結(jié)構(gòu)本身的特性與材料特性所決定的，與外載和初始條件無關(guān)。一個N 自由度線性結(jié)構(gòu)系統(tǒng)，其運動微分方程為:

式中［M］、［C］、［K］分別為系統(tǒng)的質(zhì)量，阻尼及剛度矩陣，［M］、［K］為實系數(shù)對稱矩陣，而［C］則為非對稱矩陣，因此方程(3.1)是一組耦合方程。

對式(3.1)兩邊進行拉氏變換，可得:

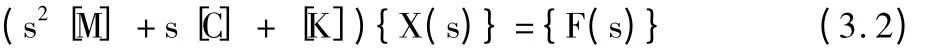
令s=jw，則式(3.2)變?yōu)?

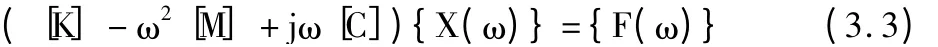
這是一組耦合的方程組，為了解耦，引入模態(tài)坐標(biāo):

式中［Φ］為振型矩陣，{q}為模態(tài)坐標(biāo)。

將式(3.4)代入式(3.3)得:

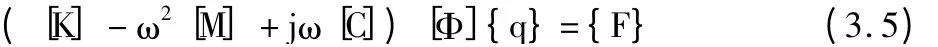
根據(jù)振型矩陣對于質(zhì)量和剛度矩陣的正交性關(guān)系，可以得到:

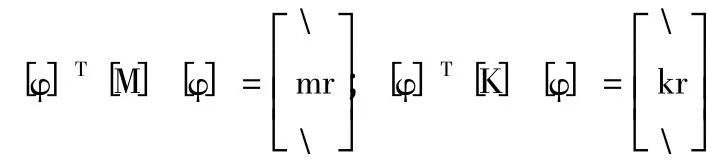
對式(3.5)兩邊左乘［Φ］T得:

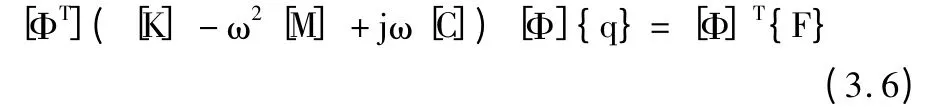
于是，相互耦合的N 自由度系統(tǒng)的方程組經(jīng)正交變換后，第i 個方程為:

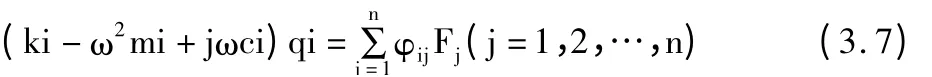
在任意坐標(biāo)下，其響應(yīng)為:

從式(3.8)可知，采用模態(tài)坐標(biāo)后，N 自由度振動系統(tǒng)的響應(yīng)，相當(dāng)于在N 個模態(tài)坐標(biāo)下單自由度系統(tǒng)的響應(yīng)之和，這就是模態(tài)疊加原理。在模態(tài)坐標(biāo)下的質(zhì)量mi、剛度ki、阻尼ci及固有振型φi，均稱為模態(tài)參數(shù)。采用歸一化方法，使模態(tài)質(zhì)量歸一，記模態(tài)質(zhì)量歸一化振型為Φ，典型的無阻尼模態(tài)分析求解的基本方程是經(jīng)典的特征值問題，即

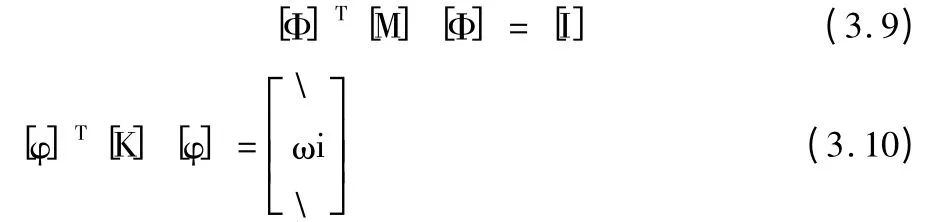
式中:

［K］:剛度矩陣

{φi}:第i 階模態(tài)的振型向量

［M］:質(zhì)量矩陣

ωi:第i 階模態(tài)的固有頻率(ω2

i 是特征值)

3.2 高速軸的模態(tài)分析計算

運用ANSYS 有限元分析軟件，采用相關(guān)的動力學(xué)模態(tài)分析方法，對路面拋丸機的高速軸進行其振動時的特性計算，從而得出有關(guān)它的有限元分析結(jié)果，即振動頻率及振型。模態(tài)分析時建模的幾何模型、所選單元類型、網(wǎng)格劃分及施加約束和靜態(tài)時相同，經(jīng)過計算處理，得到了高速軸的1 至3 階的自振頻率，其模態(tài)分析圖如圖5、圖6、圖7。

經(jīng)過分析計算得到高速軸前三階自振頻率如表2。

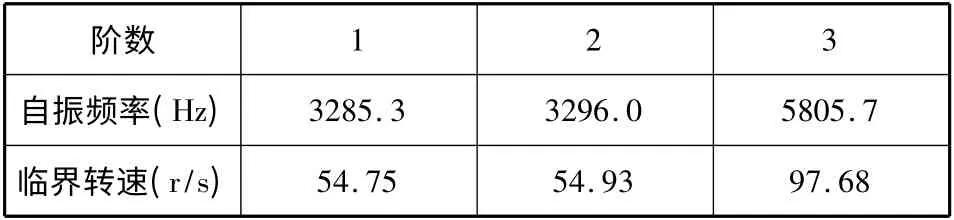
表2 自振頻率表

從表2 可以看出，在高速軸的一階、二階振動的過程中，其變形主要發(fā)生在軸端，這主要是由于高速軸受到軸承支撐的影響。因些，通常只需要研究其前面兩階的自振頻率，這是因為階數(shù)越高，自振頻率就越大，而設(shè)計高速軸的最大轉(zhuǎn)為2500r/min，而高速軸的一階自振頻率為3285.3r/min，遠(yuǎn)大于高速軸的最大轉(zhuǎn)速，所以更高階的自振頻率也將會更高，這樣將不會出現(xiàn)共振的情況，所以設(shè)計的高速軸是滿足要求的。

4 結(jié)論

應(yīng)用有限元分析軟件ANSYS 建立了高速軸的有限元模型，分析了高速軸的靜態(tài)特性，得到了詳細(xì)的應(yīng)力分布圖，為高速軸的結(jié)構(gòu)改進提供了理論依據(jù);研究了高速軸的固有振動特性，包括固有頻率和振型，并得出了比較精確直觀的結(jié)論，為進一步主軸動態(tài)特性的研究提供了依據(jù)。

［1］張丹.水平移動式拋丸機械工作原理研究及彈丸的動態(tài)仿真分析［D］.吉林:吉林大學(xué)，2007:1 -3.

［2］曾攀.有限元分析基礎(chǔ)教程［M］.北京:清華大學(xué)出版社，2008.

［3］劉元林，都維剛，宋勝偉.水平移動式拋丸機葉片受力的有限元分析［J］.黑龍江科技學(xué)院學(xué)報，2009，19(5):360-364.

［4］張義民.機械振動力學(xué)［M］.長春:吉林科學(xué)技術(shù)出版社，2000.

［5］楊康，韓濤.ANSYS 在模態(tài)分析中的應(yīng)用［J］.佳木斯大學(xué)學(xué)報，2005，23(1):81 -83.