客運專線車站股道分配方案的均衡性研究

劉 淇，王 軍，張星臣，陳軍華，杜 鵬

（北京交通大學 交通運輸學院 1.碩士研究生 2.博士研究生 3.教授 4.講師 北京 100044）

車站是客運專線鐵路運輸網絡中的關鍵節點。在車站作業中，股道分配是一項很重要的環節，車站設備的合理使用，直接關系到車站的服務水平與資源的有效配置。對于股道分配問題，限于求解規模的巨大，目前多集中在可行解的分析與建模。文獻〔1〕建立多目標股道分配模型，運用多目標規劃理論，采用分支定界法對模型進行求解；文獻〔2〕建立了以行車交叉干擾小、方便旅客出行和到發線使用均衡性為優化目標的整數規劃模型；文獻〔3〕將影響股道分配的因素分為軟約束和硬約束進行建模并求解；文獻〔4〕對運用數學規劃的方法來求解到發線運用問題，建立一個到發線運用的混合整數規劃模型。

然而，股道分配方案均衡性研究并不系統和深入。如文獻〔2〕研究了股道分配方案的均衡性問題，但對均衡性的描述簡化為全天股道被占用時間的均衡，這并不能充分說明該方案是否均衡。鑒于此，本文在分析影響均衡性分配的基礎上，建立了刻畫分配均衡性的指標，并建立股道分配的數學模型，達到評價大型客運站股道分配的均衡性目的。

1 影響股道分配均衡性的因素

客運專線股道分配均衡性是指在列車運行圖與車站平面圖的時空約束下，為列車分配無沖突的進路和站臺，使車站各股道被占用的時間和空閑間隔時間達到均衡以及方便旅客上下車。

列車在車站的行車作業包括接車、停留和發車3個部分，在此過程中需要為列車鋪排進路和安排停留到發線，以及滿足列車進行各種作業的要求等，另外在客運專線車站還要考慮到旅客乘降的舒適度，這些都會對股道的使用產生影響。影響股道分配均衡性的因素包括列車進路的選擇、車站間隔時間、列車去向及線路上下行。

1.1 列車進路的選擇 大型客運專線車站銜接方向多，一段時間內接發列車可能比較多，一列列車進路的鋪排可能會影響到其他列車進路的選擇。當選擇不適合時，會導致進路交叉，致使其他列車不能按時接到相應的股道，從而影響了車站的作業能力。

1.2 車站間隔時間 為保證車站作業的安全，只有當前行列車的尾部離開并釋放相應的軌道電路區段以后，才能為后行列車開始準備接車進路。因此，對于先后占用同一股道的2 列車，前行列車離去到完全釋放到發線的時間，與后行列車開始占用到發線的時間之間的間隔，應滿足一定的安全間隔時間。

1.3 列車去向及線路上下行 在不考慮其他條件約束的情況下，車站各股道都可以接發任何去向的列車。但是這樣就會產生諸多交叉干擾，反而影響了車站的能力。因此，每個股道應有特定接發列車的方向和種類。

2 股道分配均衡性模型

由于不同的時間段，列車到發的數量有區別且車站股道使用的目的也有區別，因而高峰時期，由于列車到發多，車站可能更多地考慮車站各股道使用均衡性；而在低谷時間段，車站可能更多地考慮如何滿足旅客上下車的舒適性。為此，需要對高峰期和低谷期2種情況分別建立模型。

2.1 高峰期目標函數 根據影響股道分配均衡性的因素，建立以股道總體使用均衡性和各股道使用空閑時間均衡性為優化目標。

1）目標函數1：各股道被占用時間均衡的目標函數（見式1），表明目標函數值越小，股道使用越均衡。

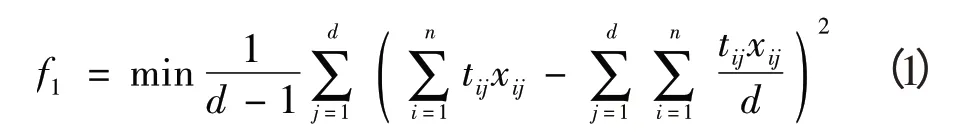
式中：d為車站的股道數；

n為車站一天內到發列車數；

tij為第i 列車接發到到發線j 的總時間，tij=tsi+tLi+tEi；tLi為第i 列車占用到發線時間，由出發時刻和到達時刻得到；

tsi為第i 列車出發作業時間，由車站技術作業標準得到；

tEi為第i 列車到達作業時間，有車站技術作業時間標準得到；

Xij表示第i列車是否使用第j條股道，0，1變量；當Xij=1時第i列車由第j股道接發。

2）目標函數2：股道空閑時間均衡的目標函數（見式2），表明目標函數值越小，股道使用越均衡。

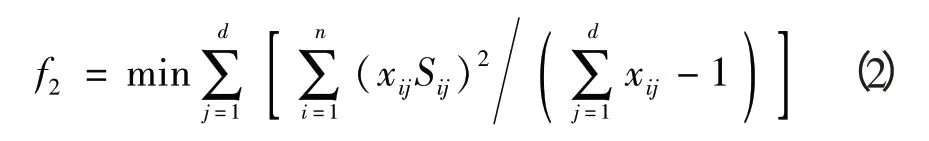
式中：Sij表示第j股道分配給2個相鄰列車中間的空閑時間，即，表示同一股道前一列車的離開時間與后一列車到達時間的差。

2.2 低谷期目標函數 低谷期，車站列車比較少，此時要以提高服務質量、方便旅客乘降為核心，為列車安排股道。

目標函數3：方便旅客乘降的目標函數（見式3），表明目標函數值越小，更能方便旅客乘降。

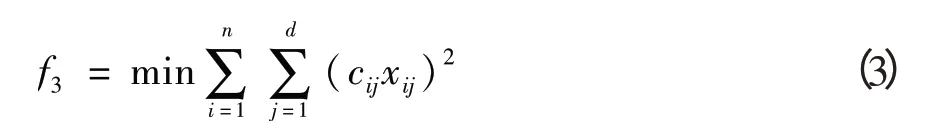
式中：Cij表示列車i使用股道j時方便旅客乘降的權重。

2.3 約束條件

1）列車去向、上下行等引起的約束。根據列車的去向、上下行和個人偏好等情況，將列車i分到對應股道集合Wi中股道進行接發。

2）一列列車至多有1條股道接發，即

3）在一段時間內，1 條股道只能被1 列車占用。記列車i 占用股道j 的時間為，在該段時間內股道j不能在被其他的占用：

式中：tj表示股道j被占用的時間；

ZjW表示j是否被占用，0，1變量；當ZjW=1表示被占用，否則，ZjW=0表示未被占用。

4）進路沖突約束。進路的沖突分為時間沖突和空間沖突。時間沖突是由列車運行圖產生的，時間沖突可以通過分配無沖突的空間資源解決；空間沖突需要給予沖突的作業分配無沖突的時間資源。因此，為2列車安排股道時，應避免2種沖突同時出現。

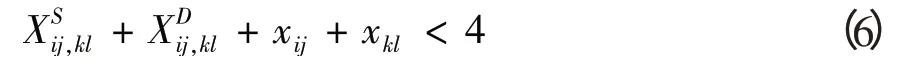
5）同一股道連續接車的時間間隔應滿足作業時間要求。假定相繼停在股道j的3列車i-1、i、i+1，則他們在車站的時間間隔約束應滿足：

Tmin為車站作業最小間隔時間。

3 模型求解

由于建立的模型是多目標非線性規劃模型，直接求解存在很大的困難，但可以采用遺傳算法進行求解。遺傳算法是一種自適應搜索算法，是優秀的全局搜索算法。

3.1 編碼形式 采用整數編碼方式，染色體長度為需要安排股道的列車數量。每個基因上的數值代表分配給該列車的股道編號。

3.2 初始群體的生成

步驟1：按照列車進站時間順序初始化列列車，記為集合N=（n1，n2，…，nk）；股道是按照車站的使用方案和空閑開始時間進行初始化，記為D=（d1，d2，…dm，）。

步驟2：產生所有列車可使用股道集合W=（W1，W2，…，Wn），W1表示列車i 可使用股道集合。列車i可使用的股道j需要滿足的約束條件包括：股道j應在列車i可使用的股道集合中；列車i的實際到達時間要晚于股道j空閑開始時間，列車i離開時間要早于股道j的結束使用時間，且相鄰兩列車使用同一股道的時間間隔不小于Tmin。

步驟3：為1 列列車生成1個隨機整數bi∈ [1,count（Wi）]，確定列車i 在可使用股道集合中的股道j，更新股道i的開始使用時間；若大于邊界時間，則在其他列車可使用的股道集合中將此股道j刪去，更新其他列車可使用股道集合；

步驟4：判斷Wi+1，Wi+2，Wi+3，…Wn中是否有空集，如果有轉步驟2；如果沒有，轉步驟5。

步驟5：判斷i=n 是否成立，如成立轉步驟6；如果不成立，則i=i+1轉步驟3。

步驟6：所有列車分配完畢，算法結束。

這樣循環n 次即可以得到種群數量為n 的一個初始群體。

3.3 適應度函數的選取 適應度函數是算法用于指導搜索方向的惟一準則。由于該問題的目標函數是取得最小值，不能直接作為適應度函數。

1）高峰期的適應度函數

適應度函數1：F1=M-f1

適應度函數2：F2=M-f2

2）低谷期的適應度函數

適應度函數3：F3=M-f3

式中：M為足夠大的數。

3.4 遺傳算子設計

3.4.1 選擇操作 采用比例選擇算子，按個體的適應度函數值采用賭輪法來決定個體被選擇的概率。

3.4.2 交叉操作 采用隨機配對策略將群體中染色體以隨機的方式組成配對染色體組，每組以一定的概率進行交叉操作。

3.4.3 變異操作 遺傳算法實現變異的方法是賦予每個基因一個相對較小的變異概率。

3.5 終止準則 根據需要，采用確定的迭代次數作為終止規則。

4 案例分析

某客運站是一個雙線通過式車站，車站銜接3個方向（A，B，C），共有股道9條，4個站臺，其中2條正線、7條到發線，該車站包括2個咽喉，B和C方向在車站的一側（見圖1）。

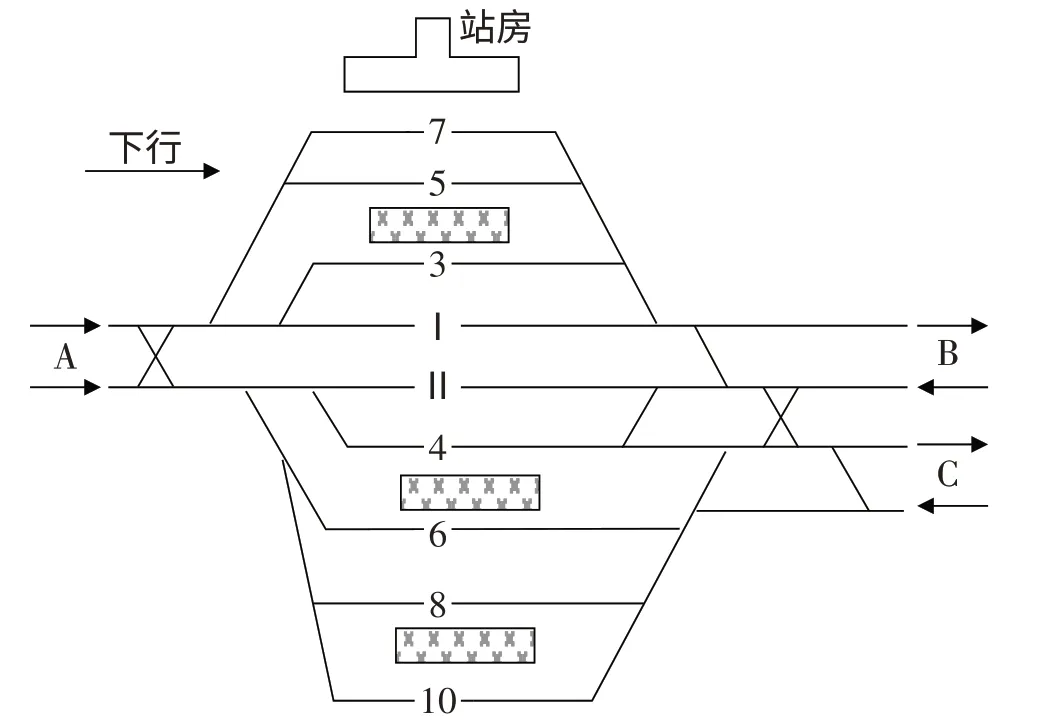
圖1 某客運站平面布置簡圖

一個高峰時間段（07：00-08：30）內有26 列車需要安排股道，且車站作業最小間隔時間為3.0 min，列車到達作業和出發作業均為4.0 min，采用JAVA語言進行編程求解。

4.1 分配方案一 僅考慮目標函數1時，股道具體分配結果如表1所示。

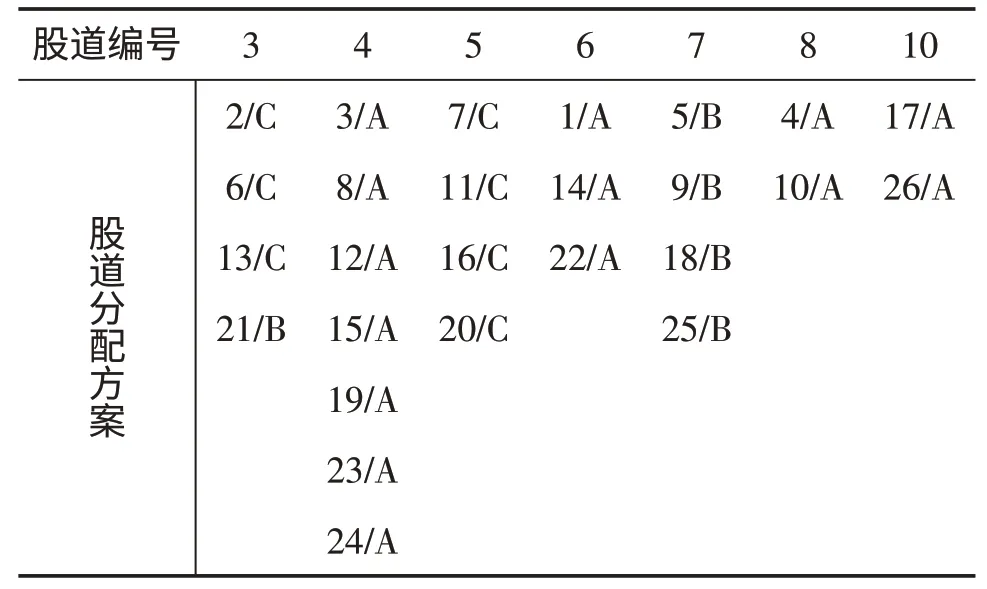
表1 分配方案一（列車編號/去向）

該方案中目標函數1 的值為2 032，目標函數2的值為1 579。

4.2 分配方案二 同時考慮目標函數1 和目標函數2，算法求解的股道分配方案如表2所示：

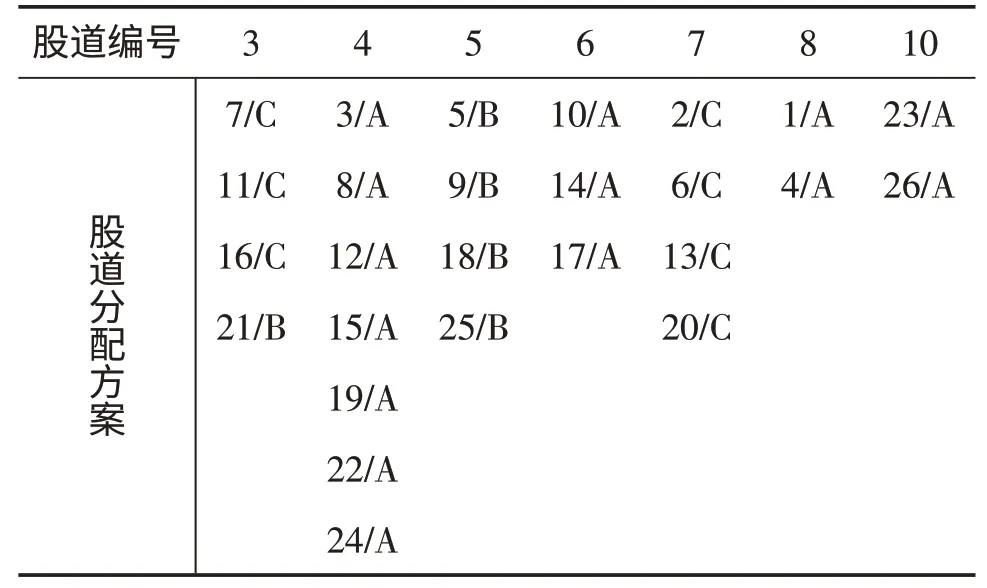
表2 分配方案二（列車編號/去向）

該方案的目標函數1 的值為2 053，目標函數2的值為417.33。

從以上2個分配方案對比可以看出，各列車均按照可利用的股道集使用股道，A 去向的列車選擇股道4，6，8，10，B 去向和C 去向列車選擇股道3，5，7；上下行靠近站房的股道4，5，7 安排的列車較多，方便旅客乘降；每個股道的列車數為2～7 列，從數量上看比較均衡。與分配方案一相比，分配方案二的目標函數1 值僅大了20，但是目標函數2 值卻小了很多。因此，分配方案二比較均衡。

5 結束語

本文從車站的高峰期和低谷期情況考慮，分別建立了多目標的股道分配均衡性模型。高峰期以股道占用時間和股道空閑間隔時間均衡性為優化目標，建立股道分配均衡性模型；而低谷期以方便旅客乘降為優化目標，建立股道分配均衡性模型。而后，采用遺傳算法對模型進行求解，該算法可以縮小搜索空間，提高模型的求解效率。最后，以某一客運站高峰時期對模型進行了驗證，通過2個分配方案的對比可以看出，評價車站股道使用方案的均衡性，要綜合考慮股道占用時間和股道空閑時間間隔的均衡性2個方面。

〔1〕雷定猷，王 棟，劉明翔.客運站股道運用優化模型及算法〔J〕.交通運輸工程學報，2007，7（5）：84-87.

〔2〕林志安，潘玲巧.鐵路客運站到發線分配問題研究〔J〕.鐵路運輸與經濟，2010，32（10）：58-61.

〔3〕賈文崢，毛保華，何天健，劉海東.大型客運站股道分配問題的模型與算法〔J〕.鐵道學報，2010，32（2）：8-13.

〔4〕Carey.A model and strategy for train pathing with choice of lines，platforms and routes〔J〕.Transportation Research B.1994.

〔5〕Zwaneveld，Kroon.Routing trains through a railway station based on a node packing model〔J〕European Journal of Operational Research，1999.

〔6〕謝楚農，黎新華.鐵路客運站到發線運用優化研究〔J〕.中國鐵道科學，2004，25（5）：130-133.

〔7〕魯工圓.客運專線車站作業仿真系統的研究及應用〔D〕.成都：交通運輸規劃與管理，2007.

〔8〕呂紅霞.鐵路大型客運站作業計劃智能編制的優化技術和方法研究〔D〕.成都：交通信息工程與控制.