電動舵機伺服控制器的設計與研究
趙志剛,林 輝,張慶超,張 韜
(西北工業大學,陜西西安710129)
0 引 言
舵機系統是飛行控制系統中不可或缺的關鍵組成部分,它的特性優良與否直接影響飛行控制系統的整體性能。電動舵機系統的任務是接收飛行器飛行過程中導航計算機的位置給定信號,并實時、快速、精確地控制飛行器舵面的偏轉,使舵面精準地跟蹤導航計算機的位置給定信號。所以,舵機系統是一個典型的位置隨動系統,舵機控制系統的動靜態性能指標直接決定了飛行器的飛行軌跡。
本文介紹了基于TMS320F2812 和三菱公司的智能功率驅動芯片PM75RLA120 舵機伺服控制器,對系統進行了硬件和軟件設計。從機械結構到伺服部件和控制器的主控芯片的選擇,力求簡單、緊湊和可靠。根據其特點及要求精度,采用結合模糊控制規則的抗積分飽和PID 控制器。
1 系統設計
1.1 結構設計
電動舵機伺服控制系統的結構如圖1 所示。
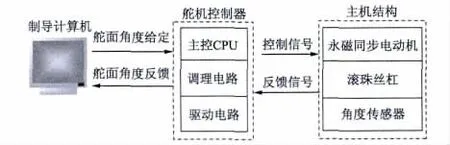
圖1 電動舵機控制系統的結構圖
舵機系統主要由舵機控制器、PWM 功率模塊、伺服電機、減速器、位置傳感器等部分組成。整個舵機控制系統接收位置信號控制指令,以及電機反饋電流、速度、舵面偏轉角度信號,經過舵機控制器計算,輸出控制信號,從而帶動舵機伺服電機按一定的規律作動,并經過滾珠絲杠結構至舵機軸輸出。這樣形成了一個舵機位置閉環的伺服作動系統。
1.2 控制器的硬件整體構成
舵機伺服系統結構如圖2 所示。
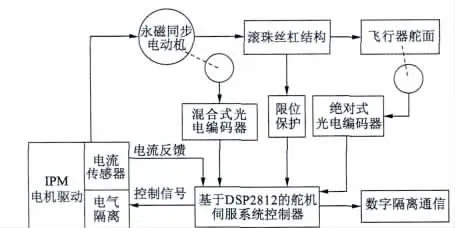
圖2 舵機伺服結構框圖
從圖中得知,硬件電路的設計包括:控制單元電路、隔離驅動電路、IPM 功率模塊電路、通信電路以及對各路反饋信號的調理電路。其中,混合式光電編碼器有ABZ 信號和UVW 信號,UVW 用于測量轉子初始位置,ABZ 用于測量轉子角度及電機轉速。舵面偏轉角度由絕對式光電編碼器測得,編碼器采用SSI 通信協議,根據系統的控制需要,DSP 的I/O口產生編碼器所需的使能和時鐘信號,編碼器將位置信號以數字量輸出給特定的I/O 引腳,通過計算得出位置的絕對角度值。
1.3 控制器的軟件整體構成
軟件上采用id= 0 控制策略,采用“位置環PID+ 速度環PID + 電流環PID”的控制方法,其中絕對式光電編碼器用于位置反饋,轉子位置的微分作為速度環的反饋,電機線電流作為電流環的反饋。考慮機械諧振、力矩耦合及電氣參數波動等非線性不確定因素的影響,采用結合模糊規則的抗積分飽和的PID 控制器。
2 硬件設計
2.1 硬件結構
舵機控制器的硬件結構框圖如圖3 所示。
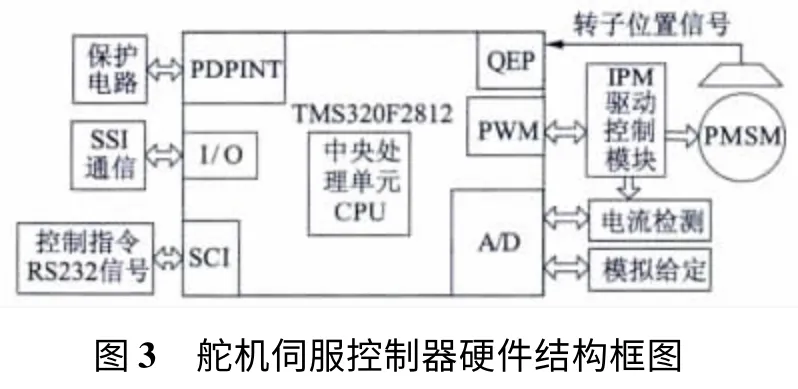
控制器以TMS320F2812 為核心,通過智能功率驅動芯片驅動電機旋轉;舵面轉角給定可以通過模擬信號給定,也可以通過串口通信給定。
2.2 硬件電路設計
控制器采用TI 公司的TMS320F2812。電機選用永磁同步電動機,它的驅動采用三菱公司的智能功率驅動模塊PM75RLA120,并使用專用驅動電源JS159,驅動模塊還具有制動控制,以及過電流、過熱、欠電壓、交叉導通保護等功能。采用ACS758 進行相電流檢測,ACS758 的輸出端經過減法器限壓,可選用巴特沃斯低通濾波器對其進行二階濾波。
3 軟件設計
3.1 系統軟件設計流程圖
舵機伺服系統采取模塊化編程設計,系統分為主程序模塊和中斷服務程序模塊,軟件總體結構如圖4 所示。
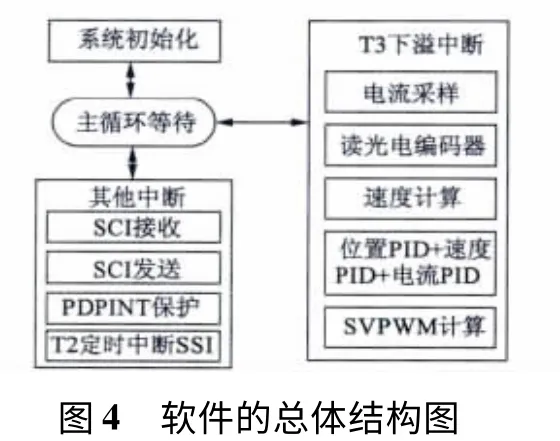
T2 定時中斷用于產生編碼器所需的使能和時鐘信號,并通過I/O 引腳電平計算出位置的角度值。
3.2 在線修正積分項的模糊PID 控制
一個PID 控制器可以被稱作一個在頻域系統的濾波器,不依賴于被控對象的數學模型,對參數變化不敏感。而采用結合模糊規則的抗積分飽和PID 控制器,使得程序調試更具靈活性,系統性能也得到很大提升,控制原理框圖及其離散形式的原理圖分別如圖5、圖6 所示。
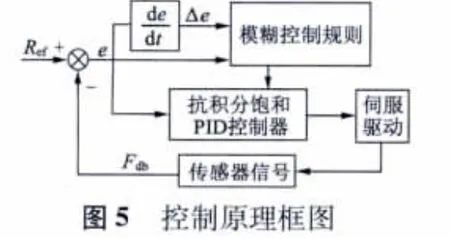
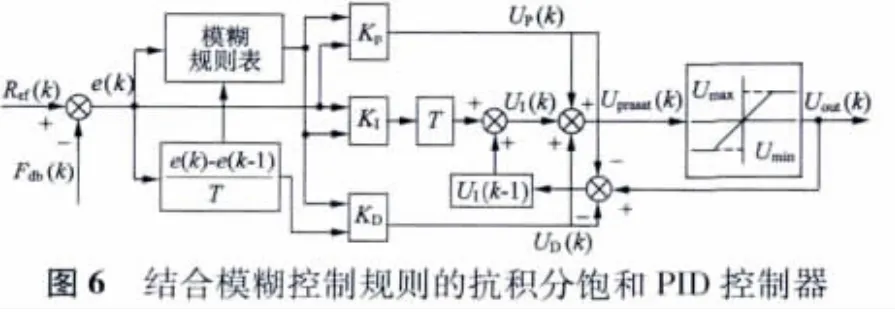
根據所設定的輸入和反饋信號,計算實際位置和理論位置的偏差以及當前偏差的變化,并根據模糊規則進行模糊推理,最后對模糊參數進行解模糊,輸出PID 的比例、積分、微分系數。
模糊控制器的輸入為誤差e、誤差變化率Δe,輸出量為U,采用相同的的模糊集,隸屬函數采用對稱、均分、全交迭的三角形。模糊集:e,Δe,U∈{NB,NS,ZO,PS,PB};模糊變量設定為正態模糊變量,其正態函數:
假設基本論域為[a ,b ],論域均取e,Δe,U∈{-4,-3,-2,-1,0,1,2,3,4},采用公式對其進行歸一化,論域轉化為[-1,1]內。
表1 為得出的模糊控制量U。采用加權平均判別法進行去模糊化,得到U 的實際輸出量。

表1 模糊控制量U
本系統與傳統抗積分飽和PID 控制器不同,控制器積分項的特別設計避免了抗積分飽和參數的調試,使得參數更易于調節。其離散方程如下:
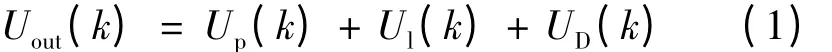
其中比例項:

在線修正的積分項:
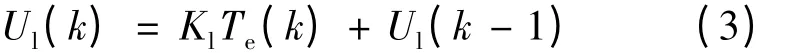
微分項:
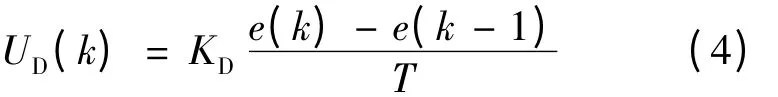
下一時刻的積分項:
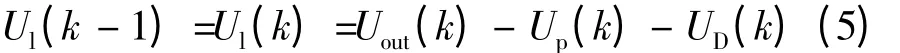
式中:Uout(k)為PID 控制器輸出;e(k)為當前時刻參考變量與反饋變量之間的偏差;T 為控制周期;Kp為比例系數;Kl為積分系數;KD為微分系數。
積分項未飽和時:
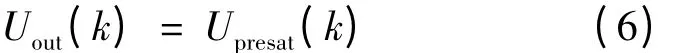
積分項飽和時:

或

根據式(5)獲取下一時刻的積分項,不會引起積分的長時間累積,使積分項處于未飽和狀態。
4 實驗結果
控制器實物如圖7 所示。

圖7 控制器測試實物
給定信號幅值為± 15°、周期為0.5 s 的方波信號,負載為100 N·m,舵機位置跟蹤曲線及其穩態誤差如圖8 所示。
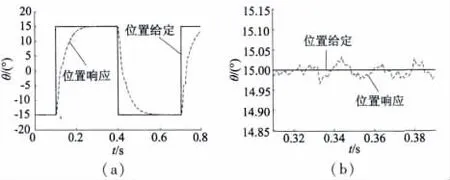
圖8 舵機位置跟蹤曲線及其穩態誤差
舵機伺服系統的最大超調量為0.5°,穩態誤差為≤0.1°,滿足設計要求。
給定信號幅值為± 15°、周期為0.5 s 的正弦信號,負載為100 N·m,舵機位置跟蹤曲線及其動態誤差如圖9 所示。
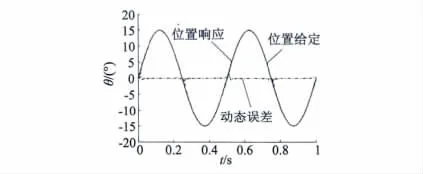
圖9 正弦波實驗結果
可以看出,系統響應速度快,動態誤差≤0.5°,滿足設計要求。
5 結 語
本文介紹了整個舵機伺服系統的設計,實現了位置環、速度環和電流環三閉環控制,針對機械諧振、力矩耦合等非線性因素,設計了在線修正積分項的抗積分飽和PID 控制器,并用模糊控制規則對其參數進行調節。實驗結果表明,該系統各項性能滿足指標要求,具有控制精度高、響應迅速、運行可靠等特點,具有較強的實用價值。
[1] 李兵強,林輝.新型永磁同步電機高精度調速系統[J].中國電機工程學報,2009,15:61-66.
[2] 姬偉,李奇.陀螺穩定平臺視軸穩定系統自適應模糊PID 控制[J].航空學報,2007(1):191-195.
[3] Liscou?t J,Maré J C,Budinger M.An integrated methodology for the preliminary design of highly reliable electromechanical actuators:Search for architecture solutions[J].Aerospace Science and Technology,2012,22(1):9-18.
[4] Reznik L,Ghanayem O,Bourmistrov A.PID plus fuzzy controller structures as a design base for industrial applications[J].Engineering Applications of Artificial Intelligence,2000,13(4):419-430.
[5] Savran A.A multivariable predictive fuzzy PID control system[J].Applied Soft Computing,2013,13(5):2658-2667.
[6] Karasakal O,Guzelkaya M,Eksin I,et al.Online tuning of fuzzy PID controllers via rule weighing based on normalized acceleration[J].Engineering Applications of Artificial Intelligence,2013,26(1):184-197.

