對我國兩種海堤規范設計波浪標準的風險分析

劉德輔，史宏達，王風清

(1.中國海洋大學 防災研究所，山東 青島 266003;2.中國海洋大學 工程學院，山東 青島 266100)

隨著全球氣候變暖、海平面上升等因素加劇的趨勢，臺風，巨浪，暴潮，暴雨巨災已成為影響太平洋沿岸及亞洲各國人民生命財產安全和經濟發展的重大問題。就中國而言，巨災已直接影響到沿海和內陸十多個省份數以億計人口的生命財產和經濟可持續發展。2006年桑美和碧利斯兩場臺風，共導致1 600 多人死亡和失蹤，5 000 多億經濟損失。桑美臺風誘發了7 m 巨浪和3.8 m 風暴增水，導致沙埕港952 只船舶沉沒，1 594只船舶毀壞。如果臺風延后兩小時登陸，則恰逢天文大潮，這種“三碰頭”的組合，可完全淹沒包括若干個核電站在內的福建、浙江大部分土地。其災難性后果難以估量。這種小概率極端事件的發生是完全可能的。亞洲其他國家所遭受的臺風—暴雨，暴潮災害同樣觸目驚心:1959年日本伊勢灣遭受臺風(Vera)暴潮襲擊，造成5 180 人死亡，受災人口達150 萬。1970年11月印度洋上的熱帶風暴波羅，風暴潮高達6 m，造成孟加拉國30 萬人死亡，100 多萬人無家可歸。1991年4月熱帶風暴哥奇造成14.3 萬人死亡。2008年熱帶風暴Nargis 造成緬甸10 萬人死亡。

長期以來，由于概率統計理論和方法上的限制，在港口、海岸、近海及河口城市防護工程的設計中，考慮惡劣環境條件下多種荷載共同作用組合的問題尚未得到妥善解決。多數情況下，仍停留在對實測資料多年最大值概率分析基礎上，假定年最大值服從某種分布(Gumbel，Weibull 或P-Ⅲ型分布等)，估計不同重現期對應的設計波高，水位，風速作為設計標準。由于每年只取一個樣本，忽略了概率論的一個基本定理——大數定理，造成大量有效信息無法被利用，影響到概率預測的正確性和設防標準的合理性，導致極端氣候因素誘發的潰壩，決堤巨災時有發生。這里對水利部海堤工程設計規范(SL435-2008)推薦的Gumbel 分布及交通部國家行業標準《海港水文規范》(JTJ213-98 2008 修訂版)推薦的復合極值分布(CEVD)作為設計波高概率預測設計標準進行風險評估，并介紹復合極值分布在國內外的應用，以期工程設計達到防災減災的目的。

1 一個臺風致災因素概率預測新理論—復合極值分布理論的建立

自20 世紀70年代初交通部“海港水文規范編寫組”成立以來，進行了全國各地港口的調查研究，特別是1972年3 號臺風重創大連港，有效波高6.8 m，超過了1896年臺風波高，導致大連港空前損失;1973年召開的“1972年3 號臺風研討會”，更進一步加深了對臺風波浪長期概率預測重要性的認識，有關單位開展了針對臺風特征進行臺風影響海區各種致災因素(風速、增水、波浪等)概率預測理論和計算方法的研究。

考慮到臺風影響不同海區每年出現的頻次各不相同，可用離散型隨機變量及相應的離散型概率分布表示;而臺風誘發的致災因素(風速、增水、波高等)，則可用連續型極值分布表示。二者的組合經過嚴格的數學推導，可構成一種新的極值分布模式—復合極值分布(compound extreme value distribution，簡稱CEVD)［1-2］。考慮到國內外慣用年極值系列按照某種概率模式(如P-Ⅲ型、Gumbel，Weibull 分布)外延推求不同重現期設計值的作法存在的弊端——遺漏了每年各次臺風波浪提供的重要信息，影響到概率預測結果的置信度;CEVD 模式引入了臺風每年影響不同海區的頻次，作為一組離散型隨機變量，將每次臺風過程波浪的最大值作為連續型隨機變量，將一個離散型分布和連續型極值分布組合起來，以順序統計學和測度論作為推導的理論依據，推導出了CEVD 模式。根據統計檢驗結果，臺風(颶風)影響各海區的頻次符合Poisson分布，臺風(颶風)波浪的不同特征，可采用Gumbel 和Weibull 分布，則可構成Poisson-Gumbel CEVD 分布(用于我國臺風影響海域)［2］和Poisson-Weibull CEVD 分布(用于美國墨西哥灣和大西洋沿岸)［3］。

Poisson-Gumbel 復合極值分布(CEVD):

當臺風頻次為泊松分布，波高符合Gumbel 分布時，可簡化為

式中:α=σn/S;u=ˉH－yn/α;ˉH，S 分別為各次臺風波高的平均值和均方差;σn，yn可由表1 根據波浪總個數n 查得。

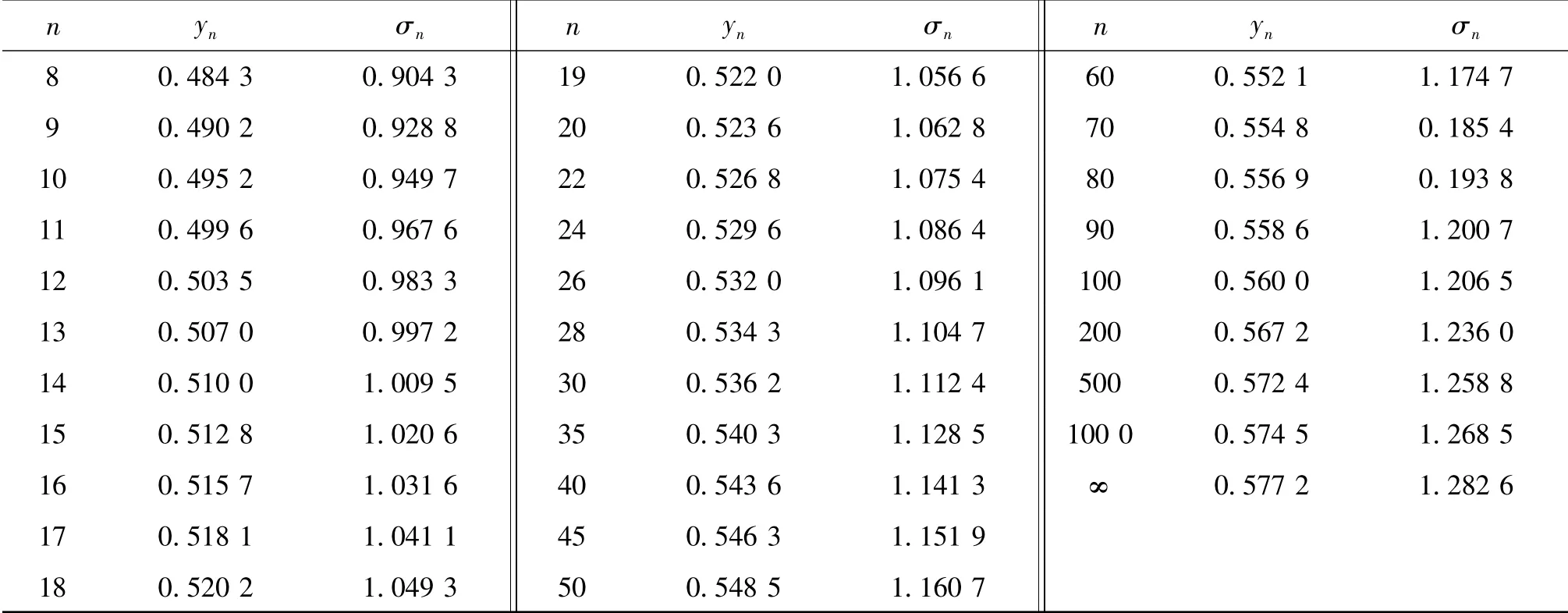
表1 yn、σn 與波浪總個數n 關系Tab. 1 Parameters yn and σn for different wave data n

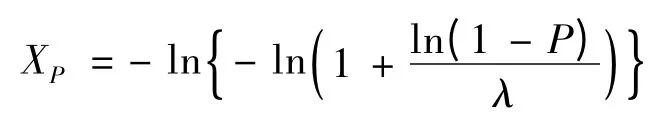
計算置信區間的計算公式如下［4］

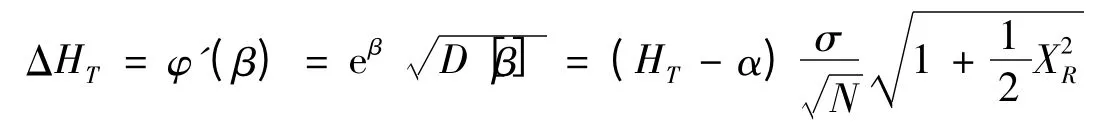
置信區間(置信概率68.27%)為［HT+ΔHT，HT－ΔHT］。

2 P-Gumbel，Gumbel 和P-Ⅲ三種設計波高概率預測模式實例計算及誤差評估

2.1 臺風過程取樣與傳統的年極值取樣的比較

用臺風過程取樣代替傳統的年極值取樣是復合極值分布的最大優點，可使用多于年極值取樣λ 倍的資料信息，減低了概率預測結果的誤差，從而提高了概率預測結果的可靠性和合理性。表2 顯示我國沿海臺風影響頻次平均高于年極值取樣的4 至6 倍，以香港為例，年極值取樣47 個樣本資料，而CEVD 臺風過程取樣則可使用291 個樣本資料信息。

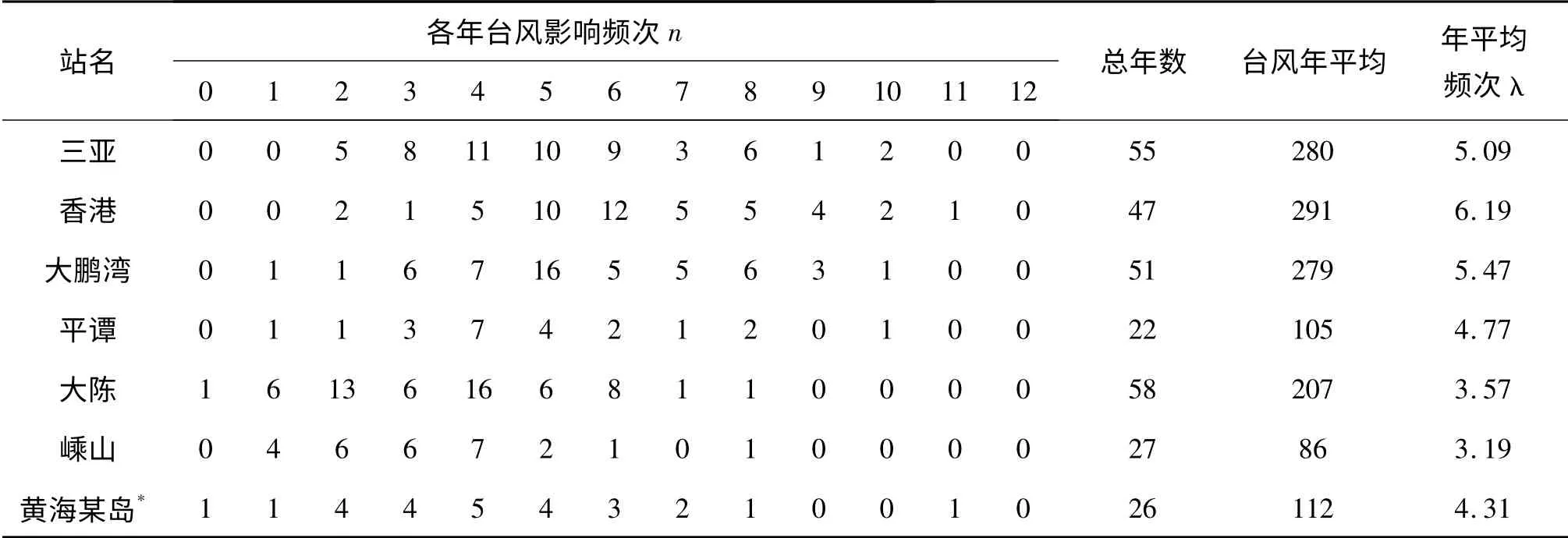
表2 我國東南沿海臺風影響頻次統計表Tab.2 Typhoon occurrence frequency in China's south-east coasts

說明:國家行業規范“海港水文規范”專題“臺風影響海區設計波浪概率預測理論和計算方法”經謝世楞院士等專家組審查，批準正式納入2008年“海港水文規范”修訂稿條文。由于交通部海港、河港合一新規范的編制，拖延至今，即將出版。

2.2 使用滑動20年取樣資料樣本對三種模式擬合誤差檢驗

將中科院南海所提供的1951 ～2002 實測(缺測部分為后報)近岸風、浪資料，分別按各20年為一組進行滑動取樣，對Gumbel，P-Ⅲ和CEVD 分布的擬合優度，按擬合最大偏差Dn ，擬合平均差v 和擬合標準差d 進行比較，如圖1 及表3 所示(有關統計特征及擬合優度說明，詳見文獻［5］)。

如表3 計算結果和圖1 所示，無論是擬合最大偏差Dn，還是擬合平均差v 和擬合標準差d，復合極值分布的擬合偏差數均小于P-III 分布和Gumbel 分布。

2.3 P-Ⅲ，Gumbel 及CEVD 三種模式預測結果對比

以大鵬灣、黃海某島(黃海某島為海軍有關部門提供資料)及三亞的樣本資料為基礎，用P-Ⅲ，Gumbel和CEVD 三種模式進行預測，其計算結果及相對誤差見表4、5 和圖2。

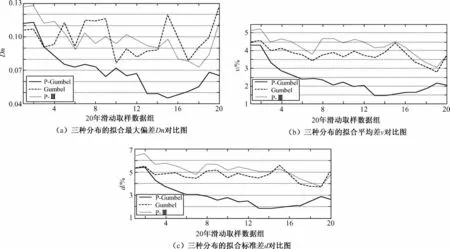
圖1 三種分布的擬合Dn，v 和d 對比圖Fig.1 Comparison of maximum deviation Dn，v and d of 3 models

表3 三種分布擬合優度參數及其變化范圍Tab.3 Comparison between confidence intervals of Dn，v of 3 models

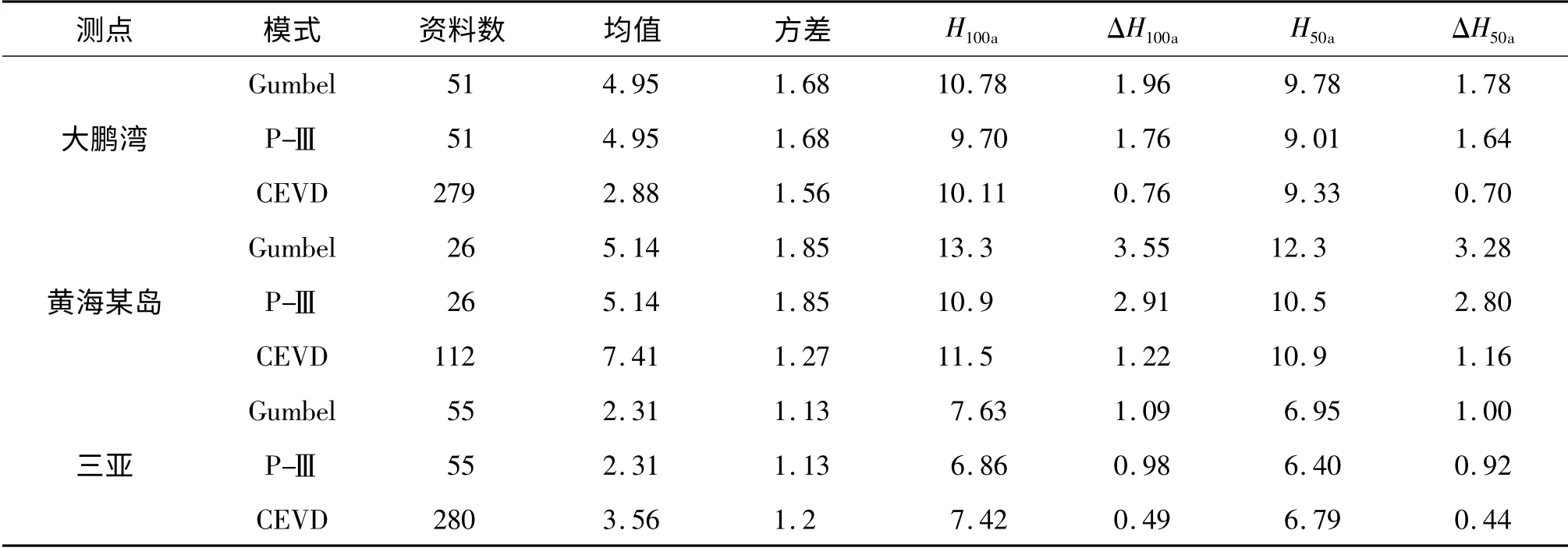
表4 幾個地點三種模式下預測計算結果Tab.4 Comparison between predicted design wave heights of 3 models with confidence intervals for Daponwa coast in South China Sea

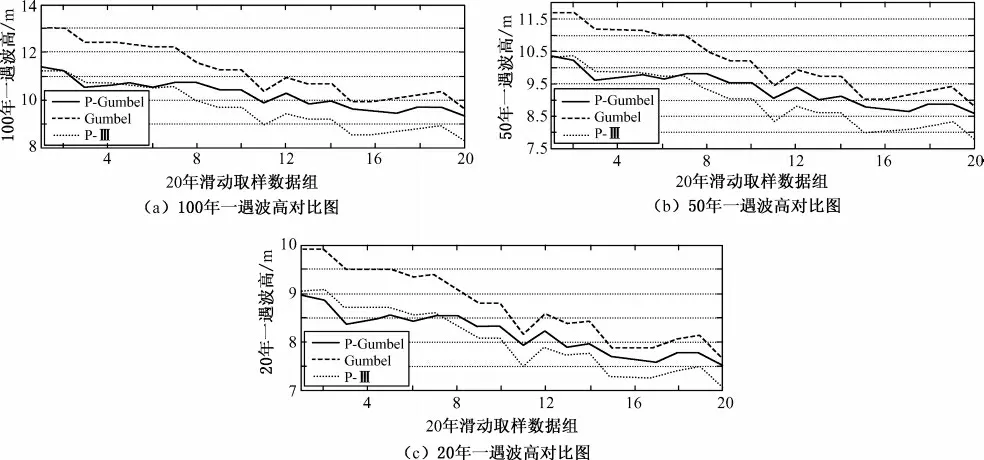
圖2 三種分布不同重現期波高對比Fig.2 Wave heights of different return periods predicted by 3 models

表5 三種分布預測值的相對誤差Tab.5 Relative error of predicted return value by 3 models

對比計算結果表明，復合極值分布的預測值介于P-III 分布和Gumbel 分布之間，這一結論與Langley R M A H El-Shaarawi［6］得出的結論是一致的。事實證明，水利規范四十年一直建議的P-III 型模式和2008年建議的Gumbel 模式，都是年極值取樣，其預測結果置信區間高于復合極值模式兩倍。

3 復合極值分布理論在實際颶風災害預測中的驗證

復合極值分布于1982年用于美國沿岸概率預測［3］。正是由于NOAA 規范的錯誤，導致2005年卡特里娜颶風巨災，證明了復合極值分布的1982年預測結果的正確性(表6)，使得復合分布在國內外大量引用和應用。2006年我們首次在災后重大國際會議上指出:按照NOAA 提出的SPH(標準設計颶風)和PMH(可能最大颶風)作為設計標準和校核標準的錯誤［7］，是這場災難的根本原因。兩場颶風的強度和特征，不僅驗證了使用復合極值分布理論1982年預測結果的正確性，同時也顯示了2005 災后使用多維復合極值分布(MCEVD)應用于卡特里娜颶風及其誘發的災害海況聯合概率分析的合理性［8-12］。如果使用CEVD 或MCEVD 預測的100年一遇和1 000年一遇致災因素作為設計標準和校核標準，Katrina 巨災是可以預防的［13-14］(見表6)。

表6 墨西哥灣A 區卡特里娜颶風強度概率分析Tab.6 Probability analysis of hurricane Katrina along Gulf of Mexico coasts

颶風的強度和特征，驗證了使用復合極值分布理論1982年預測結果的正確性。使用2002年以來新開發的多維復合極值分布理論模式——泊松–嵌套三維邏輯復合極值分布(poisson-nested logistic trivariate compound extreme value distribution，PNLTCED)分析颶風及其誘發的災害海況如圖3 所示，按照NOAA 對墨西哥灣和大西洋沿岸劃分為十一個海區后，美國學者Georgion［15］，Casson［16］和Coles［17］對上述海域極端風速預測成果，明顯低于PNLTCED 的預測值(文獻［11］中圖6)。PNLTCED 的預測結果顯示，重現期100年一遇的風速3 區(新奧爾良區)與2005 卡特里娜颶風狀況相近，明顯高于設防標準;8-9 區(新澤西，紐約沿岸)則與2012年桑迪颶風最大風速相近。

圖3 100年一遇的極端風速概率預測Fig.3 Comparison of 100-yr.hurricane wind speeds by using different methods

同樣，1982年預測的風暴增水(文獻［3］中的圖8)，費城(圖中虛線)的100年一遇風暴增水達到3 m，完全被2012年桑迪颶風造成新澤西、紐約、特拉華州大面積淹沒的事實所證實(見圖4)。

迄今為止，該理論在國內已有45 項工程中應用于設計波高概率預測，并在美國、加拿大、韓國、毛里塔尼亞、地中海、挪威等多項工程中引用和應用［6，18-22］。2008年美國在防護颶風災害工程研究中［22］，引用了四篇論文［2-3，8-9］作為防護颶風災害設防標準的依據。國家防汛抗旱總指揮部辦公室委托完成的“中國沿海臺風災害區劃、防臺風標準應急制定、防臺風應急評估標準制定”正式用于防災工作實踐［23］。

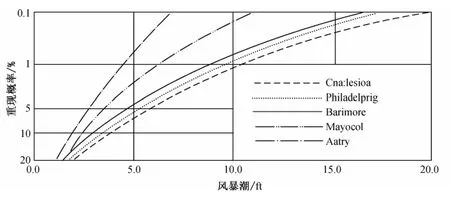
圖4 美國大西洋沿岸不同重現期風暴增水Fig.4 Long term distribution of hurricane storm surge

4 結 語

對比兩種規范條文中分別建議采用Gumbel 分布和復合極值分布用于設計波高概率預測，前者基于年極值取樣，復合極值分布以過程取樣代替傳統的年極值取樣，可使用更多的資料信息，有嚴格的理論推導為依據，減低了概率預測結果的誤差，從而提高了概率預測結果的可靠性和合理性。重大海岸工程設防標準的確定，絕非簡單的學術問題。卡特里娜和桑迪颶風災害的教訓，必須引以為戒。

致謝:對邱大洪院士、謝世楞院士及中交一航院、三航院、四航院、海軍設計總局、中科院南海所有關專家二十多年來對本理論研究提供的建議、資料和工程應用，深表謝意。

［1］劉德輔，馬逢時.極值分布理論在計算波高多年分布中的應用［J］.應用數學學報，1976(1):23-37.

［2］Liu T F，Ma F S.Prediction of extreme wave heights and wind velocities［J］.Journal of the Waterway Port Coastal and Ocean Engineering，ASCE，1980，106(4):469-479.

［3］Liu T F.Long term distribution of hurricane characteristics［C］//Offshore Technology Conference，Houston，USA，Proceedings of OTC 4325.1982:305-313.

［4］Liu D F，Kong L S，Zuo J C，et al.Stochastic-numerical model of tidal current field for Jiaozhou bay of Yellow sea［C］//Proc.ISOPE.2001，3:682-685.

［5］Ochi M K.Applied Probability and Stochastic Processes in Engineering and Physical Sciences［M］.A wiley-interscience publication，JOHN WILEY ＆ SONS，US.1990.

［6］Langley R M，El-Shaarawi A H.On the calculation of extreme wave heights:A review［J］.Ocean Eng，1986，13(1):93-118.

［7］Schwerdt R W，Ho F P，Watking R R.Meteorological Criteria for Standard Project Hurricane and Probable Maximum Hurricane Wind Fields，Gulf and East Coast of the United States［R］.NOAA Technical Report NWS 23，1979.

［8］Liu D F，Pang L，Shi H D.Joint probability analysis of hurricane katrina 2005［C］//Proc.Intern.Offshore ＆ Polar Eng.Conference(ISOPE2006).2006:74-80.

［9］Liu D F，Pang L，Xie B T.Typhoon disaster zoning and prevention criteria-a double layer nested multi-objective probability model and its application［J］.Science in China(E)，2008，51(7):1038-1048.

［10］Liu D F，Shi H D，Pang L.Disaster prevention design criteria for the estuarine cities:new orleans and shanghai-the lesson from hurricane katrina［J］.Acta Oceanologica Sinica，2006，25(4):124-130.

［11］Liu D F，Pang L，Xie B T.Typhoon disaster in China-prediction，prevention and mitigation［J］.Natural Hazards，2009，49:421-436.

［12］劉德輔，龐 亮，史宏達.卡特里娜颶風的啟示——有關海岸和水利工程的風險分析［J］.中國工程科學，2007，9(10):24-29.

［13］Bea R.Reliability assessment ＆ management lessons from hurricane Katrina［C］//Proc.Offsh.Mech.＆ Arc.Eng.San Diego.2007:OMAE2007-29650.

［14］GAO.Lake Pontchartrain and Vicinity Hurricane Protection project［R］.GAO-05-1050T，Washington D C，2005.

［15］Georgiou P N，Davenport A G，Vickery P J.Design wind speeds in regions dominated by tropical cyclones［J］.J Wind Eng Ind Aer，1983，13:139-152.

［16］Edward Casson，Stuart Coles.Simulation and extremal analysis of hurricane events［J］.Appl Statist，2000，49(2):227-245.

［17］Stuart Coles，Emil Simiu.Estimating uncertainty in the extreme value analysis of data generated by a hurricane simulation model［J］.J Eng Mech ASCE，2003:1288-1294.

［18］Kirby W H，Moss M E.Summary of flood-frequency analysis in the United States［J］.J Hydrology，1987，96:5-14.

［19］Ochi M K.Stochastic analysis and probabilistic prediction of random seas［J］.Adv Hydro-Sci，1982，13:217-315.

［20］Naffa M G，Fanos A M，Elganainy M A.Characteristics of waves off the mediterranean coast of Egypt［J］.J Coast Res，1991，7(3):665-676.

［21］Quek S T，Cheong H F.Prediction of extreme 3-sec gusts accounting for seasonal effects［J］.Structure Safety，1992，11(2):121-129.

［22］Chowdhury A G，Peng Huang，Jimmy E.Aerodynamic testing application of a full-scale facility for mitigating hurricane-induced coastal disasters［J］.Far East Journal of Ocean Research，2009，2(1):1-27.

［23］劉德輔，史宏達，龐 亮，等. 中國沿海臺風災害區劃、防臺風標準應急制定、防臺風應急評估標準制定［R］. 青島:中國海洋大學，2008.