基于交貨期的多目標一維優(yōu)化下料模型研究*

邱紅喜 ，劉 林 ，2，裴 軍

（1.合肥工業(yè)大學 管理學院，安徽 合肥 230009；2.過程優(yōu)化與智能決策教育部重點實驗室，安徽 合肥 230009）

當今，企業(yè)之間的競爭已發(fā)展成為供應鏈與供應鏈之間的競爭。給供應鏈環(huán)境下企業(yè)的下料問題帶來了新的特點，供應鏈下的下料問題普遍呈現多目標的特性，更注重供應鏈中相關環(huán)節(jié)的利益平衡。

近年來許多學者對下料排產[1]各種問題做了大量的研究。如參考文獻[2]采用離散變量優(yōu)化方法對優(yōu)化目標為廢料最短的下料模型優(yōu)化求解，并改進了優(yōu)化下料的線性模型。參考文獻[3]建立了復雜約束狀態(tài)下，以綜合資源消耗最小為目標函數的優(yōu)化下料問題的數學模型；提出并實現了非定長優(yōu)化和定長優(yōu)化相結合的兩階段一維優(yōu)化下料方法。參考文獻[4]研究了余料最小和滿足顧客需求的多目標下料問題模型，把上述模型轉化成單目標整數規(guī)劃模型用分支定界法求解。參考文獻[5]研究了由交貨時間限制較大規(guī)模的單一原材料下料問題模型，針對該型提出DP貪婪算法發(fā)現下料問題主要局限于單一的下料生產環(huán)節(jié)，建立的目標和約束也沒有充分考慮復雜的生產環(huán)節(jié)。本文構造一個基于余料和交貨期懲罰的多目標模型。利用改進的非支配排序遺傳算法來求解該模型的Pareto最優(yōu)解集。并通過實驗仿真來驗證算法的有效性，從而為改進企業(yè)生產模式、提高企業(yè)整體競爭力提供了一種新的途徑。

1 多目標優(yōu)化的數學模型

1.1 模型假設

在充分了解并分析了實際情況后，對一維下料問題提出如下假設：

（1）每種坯料都有各自的交貨期，若某種坯料無交貨期，則記該坯料交貨期為無窮大。

（2）每天下料的數量受到企業(yè)生產能力的限制，每天下料的數量等于最大下料能力。

（3）切割時由鋸縫、改換模具以及廢料處理問題等一些因數產生的損耗在此不作考慮。

1.2 基于交貨期的一維下料模型

設某企業(yè)現有若干根長為L的原材料，需要截成m種不同長度規(guī)格的坯料。每種坯料都有各自的交貨期tj，如何截取，從而使第一目標是“余料最小”；其次，因企業(yè)一些特殊原因造成坯料不能按期交付，因此“不同交貨期的懲罰最小”成為第二目標。

上述下料問題的多目標下料數學模型如下：

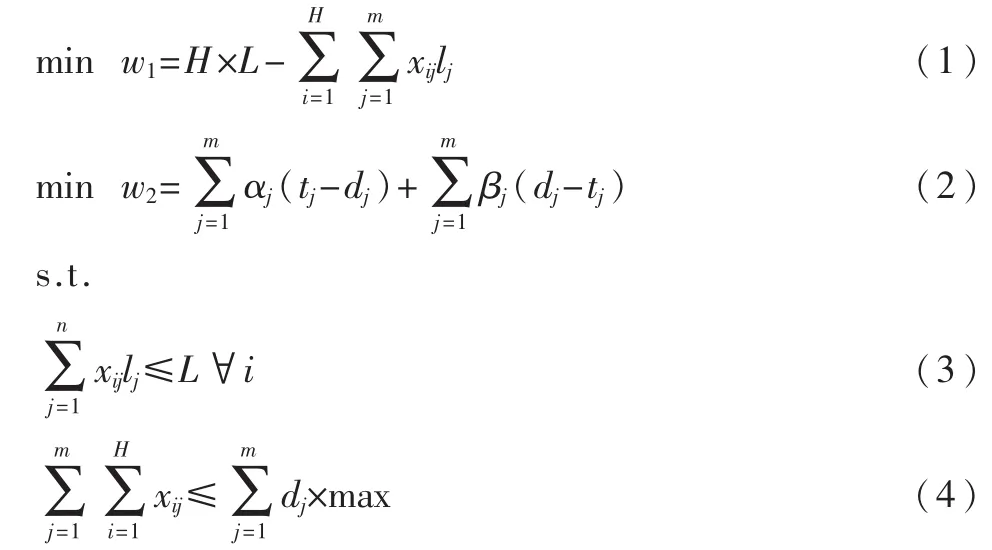
xij≥0 且 為整數 ?i，j

其中：式（1）為余料最小的目標函數；式（2）為交貨期滿意度最好的目標函數；式（3）為原料長度的約束條件；式（4）為下料的數量不能超過企業(yè)的生產能力的約束條件；i表示原材料的編號；j表示坯料種類編號；H表示原材料的使用數量；lj表示第 j種坯料的長度；xij表示從 i號原料上截得第j種坯料的數量；dj表示第j種坯料的實際完工時間；T1～T2表示合理的交貨期區(qū)間；tmin表示最早的交貨期；tmax表示最遲的交貨期；max表示企業(yè)每天最大的生產能力。

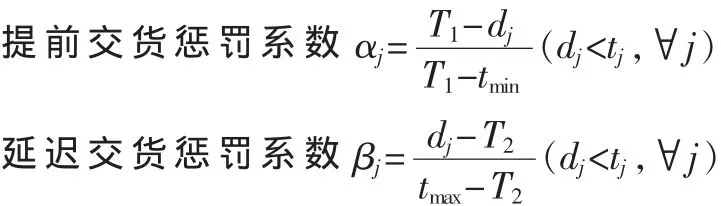
2 模型求解

隨著問題規(guī)模的增大，組合優(yōu)化問題的搜索空間急劇擴大，并且多為非線性規(guī)劃問題，所以也是一個NPHard問題。大多數對于這樣問題，一般無法得到最優(yōu)結果或無法及時得到最優(yōu)結果。人們已意識到應該把主要精力放在尋求其非劣解上。本文采用改進的非支配排序遺傳算法[6]，求解該模型的優(yōu)化下料問題不僅可以避免早熟收斂，還提高了收斂速度。

2.1 編碼

編碼方式也稱為基因表達方式，種群中的每個個體，即每個染色體是由基因構成的。根據一維下料問題的特點，選擇用坯料的一個全排列作為一個下料方案，構成一個染色體，其中每個坯料作為基因。初始群體由需求的坯料隨機排列產生。例如：有待切的坯料5種，依次給每種坯料編號（1～5），這樣每個染色體的長度都是固定的。原料要切出1個1號坯料，3個2號坯料，2個3號坯料，1個4號坯料，1個 5號坯料，隨機產生序列（5，2，1，4，3，3，2，2）就是群體中的一個個體。

2.2 擁擠距離

把非劣解集中的解（即每個個體）按某一維目標函數降序排列，處于邊緣的個體分配給它以無窮大的距離，而剩下每個個體的擁擠距離可以通過計算同級別與其相連的兩個個體在每個目標上的距離差之和來求取。擁擠距離大的個體參與繁殖和進化的機會較多，從而維持種群的多樣性。擁擠距離的計算是為確保算法能收斂到一個均勻分布的Pareto曲面。

2.3 非支配排序

非支配排序的具體過程：首先找出當前種群中非支配最優(yōu)解并分配等級1；然后將這些個體從種群中移出，在剩余個體中找出新的非支配解，再分配等級2；重復上述過程，直至種群中所有個體都被設定相應的等級。

2.4 遺傳算子

（1）選擇算子

本文采用聯賽選擇的方法，即在群體中，隨機抽取（取值為2）個體，兩兩比較，非支配排序等級和擁擠距離皆優(yōu)者保留，直到滿足群體規(guī)模。如果兩個個體的非支配排序等級不同時，則優(yōu)先考慮等級低的個體；如果兩個個體等級相同，則優(yōu)先考慮較不擁擠的個體。

（2）交叉算子

交叉算子如果采用經典的單點交叉算子，產生的新個體有可能出現重復或缺失某些基因，導致該個體不合法。因此交叉算子的設計采用順序交叉的方案，方法是由一染色體隨機選出一個子串，復制到一個空染色體中，形成原始后代，然后另一染色體去掉和子串重復的基因，按順序從左到右補齊原始后代染色體的空缺位置，這樣就得到了一個新的后代染色體。采用該方法可以防止后代染色體出現重復的基因或缺失基因，從根本上保證了該個體的合法性。

（3）變異算子

變異算子的設計采用K-交換變異的方案，即在每個染色體中以概率P隨機選取染色體上的兩點，進行2-交換。文中采用的變異算子皆為2-交換變異。

2.5 算法流程

非支配排序遺傳算法步驟：

（1）隨機產生規(guī)模為 n初始化種群 P0，初始代數為g=0；

（2）非支配排序后，通過遺傳算法的選擇、交叉、變異三個基本操作得到第一代子代種群Q0；

（3）從第二代開始，將父代種群P0與子代種群Q0合并，此時種群規(guī)模變?yōu)?n，進行快速非支配排序，同時對每個非支配層中的個體進行擁擠距離計算；

（4）根據非支配關系以及個體的擁擠距離選擇合適的個體組成新的父代種群；

（5）采用順序交叉算子執(zhí)行交叉操作；

（6）采用2-交換變異方案執(zhí)行變異操作；

（7）判斷是否達到終止條件，達到則算法結束，否則返回步驟（3）。

3 算例

下面給出一個例子說明上述算法的有效性。

例：下料所使用的原料長度L=2 000 mm，按企業(yè)的實際生產規(guī)模，需要32種配切的坯料，各坯料的交貨期都為一周時間，最早交貨期期為3天，最遲交貨期為10天，產品合理的交貨期為5～6天。各坯料的長度和需求量如表1所示。本算例中算法的種群規(guī)模為30～50，最大進化代數為 100，交叉概率為 0.25，變異概率為0.001。

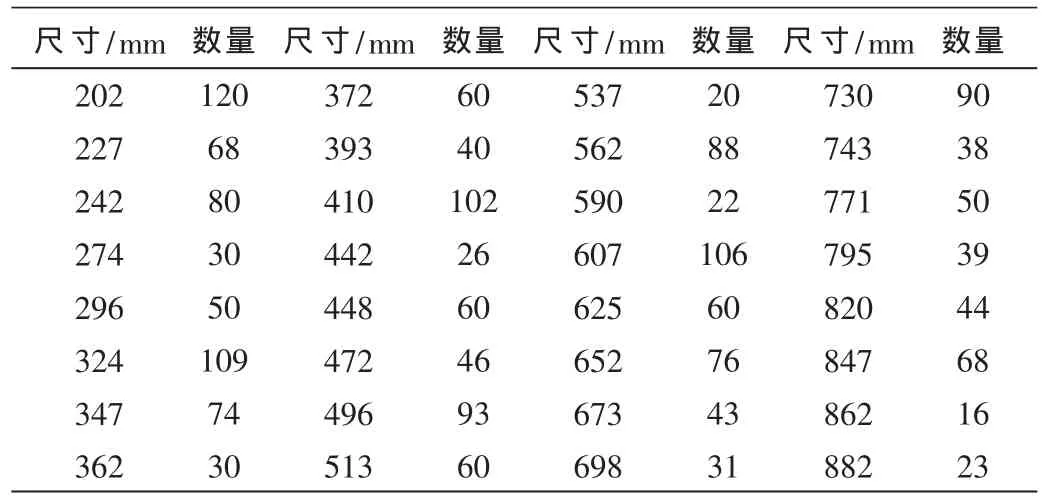
表1 坯料重量與需求量

使用Delphi7語言編程，經單機運行得出Pareto最優(yōu)解集如表2試驗結果所示。

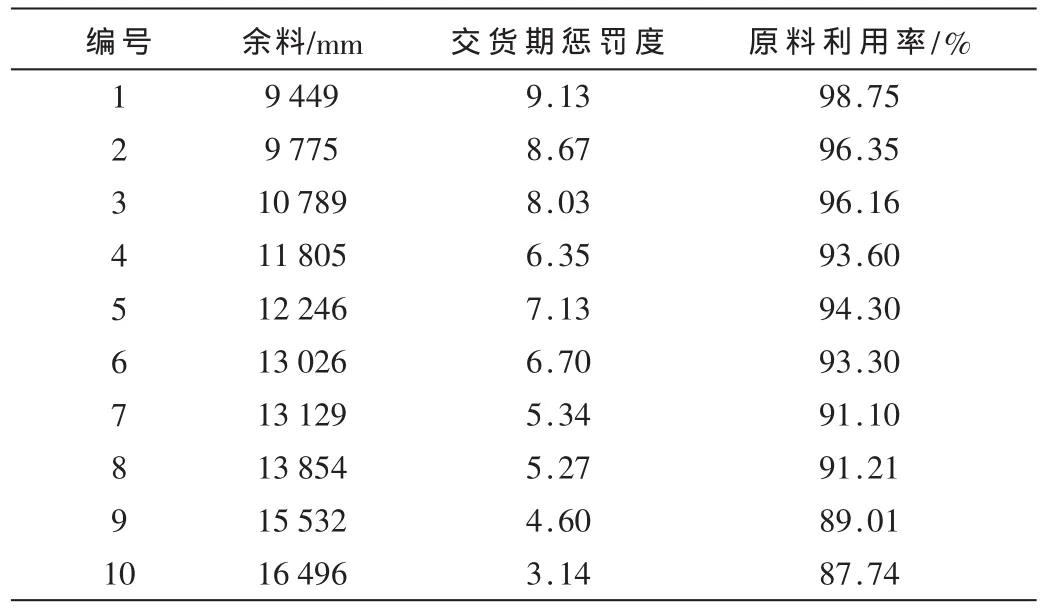
表2 試驗結果

表3給出了改進的非支配排序遺傳算法與非支配排序遺傳算法比較結果。各算法的種群規(guī)模均取30～50，進化代數為均為100。利用參考文獻[7]中的公式來比較最大散布范圍、分布均勻性。最大散布范圍的值越大，則表示散布范圍越廣；分布均勻性的值越小，則表示散布越均勻。

表3 兩種算法比較

結果表明，改進的非支配排序遺傳算法所獲得Pareto解集較為穩(wěn)定，解分布均勻，沒有出現過陷于局部最優(yōu)的情況。

改進的非支配排序遺傳算法在解決多目標優(yōu)化問題中表現出較好的性能，但仍然存在理論體系不夠完善、實現方法不太成熟等問題。本文的研究工作，今后可以從以下幾個方面進一步深入研究：（1）對于非支配排序遺傳算法的繼續(xù)深入研究和改進。（2）問題優(yōu)化得到是一組Pareto解集，還需從這組Pareto解集中選出最滿意的解，幫助決策者選出最滿意的方案。

[1]HAESSLER R W，SWEENEY P E.Cutting stock problems and solution procedures[J].European Journal of Operation Research，1991，54：141-150.

[2]米潔.CAPP系統(tǒng)中優(yōu)化下料問題的研究[J].機械，2001，28：30-32.

[3]閻春平，宋天峰，劉飛.面向可加工性的復雜約束狀態(tài)下一維優(yōu)化下料 [J].計算機集成制造系統(tǒng)，2010，16：195-201.

[4]林曉穎，王遠.多目標優(yōu)化下料問題的研究[J].哈爾濱師范大學自然科學學報，2003（5）：14-16.

[5]王輝，朱珠，張志敏.有交貨時間限制的大規(guī)模實用下料問題[J].數學的實踐與認識，2005，35：64-69.

[6]VARELA R， MU?OZ C， SIERRA M， et al.Improving cutting-stock plans with Multi-objective genetic algorithm[J].Communications in Computerand Information Science，2009， 22： 332-344.

[7]DEB K.Multi-objective optimization using evolutionary algorithms[M].New York： Jonh Wiley&sons Press， 2001：201-302.