E2地震作用下減隔振橋梁的抗震設計
禚 一,王 菲
(鐵道第三勘察設計院集團有限公司,天津 300142)
隨著社會經濟的高速發展,現代中心城市一旦遭遇破壞性的地震,造成的經濟損失將越來越嚴重。最近二三十年,全球發生的多次破壞性地震都造成了非常慘重的生命財產損失。一個很重要的原因是,橋梁工程在地震中遭到了嚴重的破壞,切斷了震區交通生命線,造成救災工作的巨大困難,使次生災害加重,從而導致了非常巨大的經濟損失[1]。因此,對橋梁工程進行正確的抗震設計就顯得尤為重要。以某減隔振橋梁為例,為驗證其抗震設計的可靠性,通過具體建模及計算過程,對該橋進行了地震作用下的強度和變形驗算,并以E2地震作用下的彈塑性地震響應分析作為重點進行深入探討,以期得到一些有益的結論。
1 工程概況
某減隔振橋梁,采用(25+42+28+20)m預應力混凝土箱梁,截面形式為單箱單室斜腹板箱形截面,箱梁中心處梁高2.2 m,頂板寬13.5 m,底板寬6.0 m,兩側懸臂各長3.0 m。采用縱向預應力體系。
下部結構中間墩(編號為4、5、6號橋墩)采用雙柱式門形橋墩,墩柱采用矩形截面,距墩頂30 cm處的兩柱之間設一道矩形截面橫系梁。交界墩(編號為3、7號橋墩)采用矩形墩上接蓋梁形式,蓋梁高1.8 m。橋墩尺寸為2.2 m×1.5 m,墩中心間距4.5 m,承臺尺寸5.5 m×6.7 m×2.0 m。基礎采用鉆孔灌注樁的基礎形式,樁基直徑1.2 m。
根據《中國地震動參數區劃圖》[2],工程沿線的地震動峰值加速度為0.20g,該地震動峰值加速度所對應的地震基本烈度為Ⅷ度。根據《建筑抗震設計規范》[3],設計地震分組為第一組。根據波速測試成果和《公路橋梁抗震設計公路橋梁抗震設計細則》的相關規定計算得出場地現狀地面下20 m深度范圍內的土層平均剪切波速值(vse)分別為244 m/s和230 m/s;場地覆蓋層厚度大于3 m且小于50 m的分界值。由前述兩項條件判別擬建橋梁場地的場地類別為Ⅱ類。
該橋采用了彈塑性減隔振球型鋼支座,因此,依照《公路橋梁抗震設計細則》中6.1.3條,關于規則橋梁的定義[4],該橋屬于非規則B類橋梁。因此E2地震作用下應采用非線性時程計算方法進行驗算。
2 橋梁彈塑性分析模型
2.1 三維有限元模型的建立
采用Midas Civil中的梁單元建立有限元模型,如圖1、圖2所示。3、7號墩為交界墩,4、5、6號墩為中間墩。上部結構離散為三維彈性空間梁單元;下部結構橋墩墩底采用纖維梁柱單元[5,6](塑性鉸),墩身采用彈性梁單元。由于結構考慮土體作用后,會改變上部結構的動力特性,如結構的基本周期延長,結構體系阻尼增大等[7,8],本橋采用群樁基礎,樁基與周圍土體相互作用非常顯著,不僅影響樁基的力學響應,也會影響整個橋梁結構的力學行為[9],且已有研究表明[10],根據具體相互作用問題的不同,土體對結構響應的影響并不一定是減小的。因此模型中應考慮樁-土相互作用的影響,樁側與土的相互作用采用“m”法[11]模擬,通過Midas Civil中的節點彈性支承連接實現,樁底采用固定端約束。

圖1 橋墩彈塑性纖維梁柱單元分析模型

圖2 全橋有限元模型
2.2 動力彈塑性本構模型
計算模型中混凝土纖維的單軸本構模型采用修正的 Kent-Park[12]模型,考慮了混凝土在加、卸載過程中的受壓連續剛度和強度退化效應、受拉剛化效應以及混凝土開裂后的剛度、強度退化效應;并通過修改混凝土的材料特性參數,有效地考慮箍筋對混凝土的約束作用。鋼筋纖維的單軸本構模型采用了修正的Menegotto-Pinto[13]本構模型,考慮了鋼筋反復加載過程中的Bauschinger效應和等向強化效應。上述2種動力彈塑性本構模型的應力-應變關系如圖3、圖4所示。

圖3 混凝土Kent-Park本構模型應力-應變關系

圖4 鋼筋Menegotto-Pinto本構模型應力-應變關系
2.3 橋墩截面纖維離散化
圖5給出了5號橋墩的鋼筋布置,鋼筋坐標為實際位置,外側70 mm所對應的區域為保護層混凝土,中間部分區域為核心混凝土。保護層混凝土、核心混凝土及鋼筋分別采用不同的材料本構模型模擬,橋墩墩底截面離散化如圖6所示。其他橋墩截面采用相同方法進行纖維離散化處理。

圖5 5號墩鋼筋布置(單位:cm)

圖6 5號橋墩墩底截面纖維離散化
2.4 彈塑性減隔振球型鋼支座的模擬
本橋在設計中采用了FLLGZ(Ⅱ)彈塑性減隔振球型鋼支座。該類型支座在正常使用情況下,不但具有普通球型支座承載能力大、轉角大、轉動靈活、壽命長等特點,還具有抗水平剪力、減震耗能的功能。此外,支座設置了3道水平抗力防線,即水平地震作用小于豎向承載力的10%時,剪力銷抵抗地震作用引起的水平力,約束向處于固定狀態;當水平地震作用等于或大于豎向承載力的10%時,剪力銷被剪斷,約束向處于滑動狀態,滑動后會因摩擦而耗能,外側懸臂棒因受彎變形而耗能,直至進入塑性狀態;滑移量達到規定值時,剛性擋塊限制支座繼續滑移并承受水平力,保證支座的整體性,從而防止落梁破壞。以上3道水平抗力防線使得該類支座具有可靠的安全性能。
在Midas Civil中,該減隔振支座需采用“滯后模型”進行模擬,支座布置如圖7所示。依照單向支座在約束方向提供剛度、雙向和固定支座在順橋向和橫橋向均提供剛度的原則進行設置。

圖7 支座布置示意(單位:cm)
3 自振特性分析
模態分析是檢驗動力計算模型正確性的重要手段,對本項目橋梁進行模態分析可以得到結構前5階模態分析結果,如表1所示。結構基本周期3.71 s,頻率0.269 Hz,1階振型為順橋向平動,如圖8所示。

表1 結構前5階頻率及周期

圖8 1階振型(順橋向面內平動)
4 E2地震作用下的結構彈塑性時程分析
4.1 墩柱有效抗彎剛度計算
為得到偏于安全的地震位移反應結果,在E2地震作用下,延性構件(墩柱)的有效截面抗彎剛度應采用鋼筋首次屈服時的割線剛度,參照《公路橋梁抗震設計細則》6.1.6條可計算得到各橋墩在橫橋向和順橋向的剛度調整系數,如表2所示,再通過Midas Civil中的截面特性調整系數來實現截面剛度的修正。

表2 剛度調整系數
4.2 人工地震波的模擬
本橋橋址處的地震動峰值加速度為0.20g,該地震動峰值加速度所對應的地震基本烈度為Ⅷ度。屬Ⅱ類場地,地震動反應譜特征周期為0.35 s(1區)。采用傅里葉變化及不斷迭代擬合的方法來生成人工模擬地震動時程,具體生成人工模擬地震波的方法如下:
(1)首先按照《公路橋梁抗震設計細則》,根據地震烈度、場地類別等設計參數確定設計反應譜,即期望反應譜;
(2)根據期望反應譜近似地計算出人工地震波的功率譜;
(3)再由功率譜得到的傅里葉幅值譜加上隨機相位做傅里葉逆變換并加上強度包絡線,得到近似人工地震波;
(4)計算近似人工地震波的反應譜,并用期望反應譜與計算反應譜的比值修改傅里葉幅值譜,重新生成人工地震波,不斷進行迭代,直至反應譜在控制頻率點處的誤差處于允許誤差范圍內。
采用上述方法得到的人工地震動擬合反應譜曲線如圖9所示。為考慮地震動的隨機性,進一步根據《公路橋梁抗震設計細則》,設計加速度時程不得小于3組,且應保證任意2組間同方向時程的相關系數絕對值小于0.1。經計算得到的每2條地震波的相關系數ρ最大值為0.051,均小于0.1,滿足規范要求。最終得到的3條E2地震作用下人工擬合地震動時程曲線如圖10所示。

圖9 目標譜和計算譜擬合結果對比(持時20 s;時間間隔0.01 s)
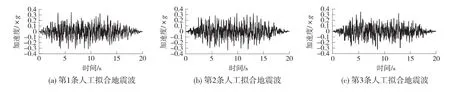
圖10 人工擬合地震動時程曲線
4.3 驗算結果分析
4.3.1 塑性區轉角驗算
順橋向及橫橋向的塑性角區域最大轉角驗算依照《公路橋梁抗震設計細則》7.4.3條進行驗算,結果如表3所示,表中取3條人工波計算結果的最大值與容許值進行比較,來判斷是否滿足規范要求。經驗算,順橋向及橫橋向塑性角區域的最大轉角驗算均滿足規范要求。

表3 塑性角區域的最大轉角驗算結果 ×10-4rad
4.3.2 墩頂位移驗算
墩頂位移的驗算,須按照《公路橋梁抗震設計細則》7.4.6條進行。由于本橋在橫橋向為雙柱墩,因此,橫橋向的墩頂位移容許值Δu應按規范7.4.8條建立彈塑性靜力分析模型,采用Midas進行pushover分析。Δd的計算參照6.7.6條。全橋模型在地震波激勵下,得到的各橋墩最大墩頂位移列于表4。經驗算,順橋向及橫橋向的墩頂位移均滿足規范要求。

表4 順橋向墩頂位移驗算結果cm
4.3.3 抗剪驗算
E2地震作用下,按照《公路橋梁抗震設計細則》7.3.4條進行墩柱塑性鉸區域順橋向和橫橋向的斜截面抗剪強度驗算。首先按照公式7.3.4條計算各橋墩順橋向及橫橋向的抗剪強度,并列于表5中。
根據纖維截面計算結果,在整個加載過程中,各橋墩墩底、墩頂最外層鋼筋均未進入屈服,因此,參照《公路橋梁抗震設計細則》6.8.1,橋梁墩柱的剪力設計值可用E2地震作用的計算結果。經表5對比后可知,各橋墩塑性鉸區域順橋向、橫橋向抗剪強度均滿足規范要求。

表5 抗剪強度驗算結果kN
5 結論
本文以某減隔振橋梁為例,采用MidasCivil建立了該橋的三維有限元模型,根據混凝土和鋼筋的材料特性,選取了適宜的動力彈塑性本構模型,考慮了樁-土相互作用的影響,模擬了彈塑性減隔振球型鋼支座,并采用人工擬合的三條地震動時程曲線對該橋進行了E2地震作用下的彈塑性時程分析,驗算了該橋在E2地震作用下的強度及變形。經過詳細的驗算與分析,驗證了本橋設計的安全性和可靠性,并為實際工程中的非規則橋梁在E2地震作用下的抗震驗算提供了一定的參考依據。
[1]葉愛君,管仲國.橋梁抗震[M].北京:人民交通出版社,2011.
[2]GB 18306-2001,中國地震動參數區劃圖[S].
[3]GB 50011-2010,建筑抗震設計規范[S].
[4]JTG/T B02—01—2008,公路橋梁抗震設計細則[S].
[5]禚一,李忠獻,李寧.基于FENAP平臺的鋼筋混凝土橋墩非線性動力分析[J].天津大學學報,43(10):906-911.
[6]禚一.鋼筋混凝土橋梁精細化建模及地震碰撞分析[D].天津:天津大學,2010,12.
[7]竇立軍,楊柏坡,劉光和.土-結構動力相互作用幾個實際應用問題[J].世界地震工程,1999,15(4):62-68.
[8]Wolf J P.Dynamic soil-structure interation[M].NewJersey:Prentice-Hall,1985.
[9]龔緯,戚冬艷.樁基礎簡化模型在橋梁抗震中的應用[J].鐵道工程學報,2008,10:17-32.
[10]王開順,王有為,李林友.土與結構相互作用地震反應研究及實用計算[J].建筑結構學報,1986,7(2):64-76.
[11]JTG D63—2007,公路橋涵地基與基礎設計規范[S].
[12]Kent D C,Park R.Flexural members with confined concrete[J].Journal of the Structural Division,ASCE,1971,97(7):1969-1990.
[13]Menegotto M,Pinto PE.Slender RCCompressed Members in Biaxial Bending[J].Journal of Structural Engineering,ASCE,1977,103(3):587-605.

