利用復合濾波算法對績效考核結果糾偏的研究

吳 林

（中鐵第四勘察設計院集團有限公司 信息中心，武漢 430063）

目前國內的績效考核主要使用關鍵績效指標（KPI）方法，由評議主體對考核對象進行打分來統計出結果。其中主要分為定量和定性兩類指標，定量指標可以通過具體的打分標準進行操作，相對來說較為準確，但是定性指標主要靠評議主體根據個人判斷打分，由于受到多種主觀因素與客觀因素的影響，以及打分的標準不同，不同的評議主體在打分結果上存在一定的偏差，不能真實反映實際的績效考核結果[1]。

為了使考核結果趨向于公平化，需要采取一些糾偏方法，對結果進行重新調整，盡可能地消除主觀因素和客觀因素的影響，使得結果真實有效。在進行糾偏操作之前，要先分析考核結果的數據特點，一般來說同一考核對象的分數符合正態分布原理，即“中間大、兩頭小”的分布規律，對于偏離正態分布有效區間的個別分數，可以剔除而不影響整個結果的真實性。

濾波算法是物理學中的常用算法，主要應用于將信號中特定波段頻率濾除的操作，是抑制和防止干擾的一項重要措施。績效考核的數據與測量系統的信號輸入數據具有類似的分布和表現特征，因此可以利用濾波算法進行糾偏操作，通過過濾干擾項和數據平滑操作獲取更加真實的結果。

1 對復合濾波算法的研究

1.1 濾波算法

常用的濾波算法包括限幅濾波法、中位值濾波法、算術平均濾波法、滑動平均濾波法、一階滯后濾波法和復合濾波法等[2]。它們的共同特點都是利用各種數學公式對數據進行分析，過濾掉對結果無用的干擾項，通過對主要數據的分析得出所需要的結果。

在實際應用中，需要根據數據樣本的特征選擇合適的濾波算法，并結合實際情況，對算法進行融合、優化，得出最合適的算法。

1.2 考核數據特點分析

根據績效考核KPI方法的特點，對不同的考核指標存在大量具有一定規律的數據信息，在考慮影響因素前提下對分數結果進行分析，其具有以下幾個特點：

（1）數據量比較大。根據KPI方法的特點，每個考核對象存在多個指標，每個指標需要多個評議主體進行打分，打分結果數量級為員工人數的平方級，數據量比較大。

（2）數據具有正態分布的特點。在針對同一個指標的打分過程中，分數結果符合正態分布的特點，大部分分數集中在相近的區域內，而偏離中心較遠的分數可以判定為干擾項。

（3）評分基準存在差異。在不同的組織機構內，由于個人主觀因素，在基準分數上存在差異性，對同樣表現的員工，有些評議主體的基準較高，有些基準較低，導致同樣表現的個人最后結果差異較大。

（4）考核對象分組靈活。為了減少結果的差異性，一般單位會對分數進行排序，并生成考核系數作為最終的考核結果。但考核對象的分組與組織機構不一定完全吻合，不同組織的人員可能會在一個隊列里面進行排序，此時基準的差異會對考核結果的系數造成較大的影響。

根據考核數據的這些特點，糾偏過程可以分為2個步驟：（1）過濾干擾項，利用正態分布的原理過濾掉過高或過低的少量分數，只對有效區域內的分數進行計算；（2）進行結果平滑，利用多種濾波算法的復合效果對考核結果進行限定范圍內的數據平滑，獲取同一基準下的考核結果。

1.3 干擾項過濾算法

在過濾干擾項時可以借鑒濾波算法中的一些方法，同時根據考核結果數據的特點對算法進行調整和優化，下面先介紹一下濾波算法中常用的算術平均法和中位值平均法，再運用正態分布原理對其改進，提出新的正態分布濾波算法。

1.3.1 算術平均濾波法

算法描述：

連續取n個采樣值進行算術平均運算。n值較大時，信號平滑度較高，但靈敏度較低；n值較小時，信號平滑度較低，但靈敏度較高。

算法分析：

適用于對一般具有隨機干擾的信號進行濾波，這樣信號的特點是有一個平均值，信號在某一數值范圍附近上下波動。但是這種算法沒有對偶然出現的脈沖性干擾進行過濾，無法消除干擾帶來的偏差。

1.3.2 中位值平均濾波法

算法描述：

相當于“中位值濾波法”+“算術平均濾波法”，連續采樣n個數據，去掉一個最大值和一個最小值，然后計算n-2個數據的算術平均值。

設數據集合為A，則去掉最大值和最小值的集合為B=A-max(A)-min(A)。

其數學表達式是：y=∑{x|x∈B}/(n_2)

算法分析：

融合了兩種濾波法的優點，對于偶然出現的脈沖性干擾，可消除由于脈沖干擾所引起的部分采樣值偏差。但是由于干擾項不僅僅存在于最大值和最小值上，在極值附近可能會有多個干擾，因此算出的結果仍然存在一定偏差。

1.3.3 正態分布濾波

正態分布又名高斯分布，是一個在數學、物理及工程等領域都非常重要的概率分布，在統計學的許多方面有著重大的影響力。若隨機變量X服從一個數學期望為μ、標準方差為σ的高斯分布，則其概率密度函數為正態分布的期望值μ決定了其位置，標準方差σ決定了分布幅度。因其曲線呈鐘形，因此又稱為鐘形曲線。通常所說的標準正態分布是μ = 0，σ = 1的正態分布。

為了盡可能地消除干擾項，需要在中值平均濾波法的基礎上進行改進，利用正態分布原理對算法進行優化，過濾掉偏離均值過遠的干擾數據，計算出有效的數據平均值。其算法過程描述如下。

算法描述：

連續采樣n個數據，計算其正態分布的期望值u和標準方差σ，通過預先定義好的有效數據比率p，把超出分布區間的m個數據過濾掉（包括過高值和過低值），對剩余的n-m個數據計算算術平均值。

設數據集合為A，其符合正態分布規律，計算出期望值u和標準方差σ，定義有效數據比率為p，區間參數為k，根據區間面積公式（u_kσ,u+kσ）=p計算出k的值。

其數學表達式是：

算法分析：

融合了正態分布和濾波算法的優點，能夠更加有效的過濾掉干擾項，使得計算結果更接近于期望值。缺點是需要先對數據進行分析，時間長、復雜度較高，并有可能會過濾掉部分真實有效的偏離數據。

1.4 平滑算法

經過干擾項過濾之后，集合內的數據能夠取得有效的平均值，但是不同集合之間的偏差依然存在，反映為各組織機構的考核對象平均分存在差異性，需要進一步消除集合之間的基準不同造成的偏差。

在進行績效考核時，一般會存在兩次分組。第1次分組是在評議打分過程中，按照人員所屬的組織機構，劃分考核對象和相關的評議主體；第2次分組是在結果計算過程中，按照崗位序列和層級對考核對象進行分組，然后在同一組中對考核結果進行排序，從而得出最終的考核結果。由于兩次分組的標準和集合不同，導致第1次分組時的基準偏差會帶入到第2次分組中，對最終的排序結果造成干擾，因此需要在不同分組之間進行平滑，消除基準不同造成的偏差。

1.4.1 窗口映射法

在計算結果之前，先定義一個數據范圍的標準窗口，固定其最低值和最高值，然后依據每個分組內的數據范圍，將其映射到標準窗口中，同時保留原來的偏差分布，在同一個基準范圍內對不同集合的數據進行統一計算[3]。

算法描述：

設考核數據集合為A1、A2、…、An，標準窗口為S，映射算法為G(A)，映射后的集合為A'k=G(Ak) (k=1，…，n)，過濾算法為y=F(A) 。

則第k個集合Ak最終結果的表達式為：yk=F(A'k)

算法分析：

將不同集合的數據放在同一個標準窗口下進行計算，能夠消除不同打分基準造成的偏差，但是在映射過程中可能會丟失原來的數據特性，使得最終結果的分布區間發生變化，不能真實反映結果之間的差距。

1.4.2 多重濾波法

該算法的核心思想是進行兩次濾波操作。根據分組的結果，將數據分為一些不同的集合，第1次在集合內部進行濾波操作，第2次把每個集合的平均結果作為新的采樣數據，再進行一次濾波操作，達到數據平滑的效果。

算法描述：

根據第1次分組的結果，將考核數據分為n個集合A1、A2、…、An，對其中的每個集合應用去干擾項的濾波算法，得出每個集合的結果平均值B={b1，b2，…，bn}，然后在集合B上應用算術平均濾波算法，得出其平均值v，計算出B中每個元素與v的差值C={c1，c2，…，cn}，最后把C中的每個差值元素應用在集合A1、A2、… 、An上對其進行平滑，得出最終的考核結果。

設干擾項過濾算法為y=F(A)，則集合B={bk|bk=F(Ak), k∈N}，集合B的平均值b與v之間的差值組成的集合C={ck|ck=v-bk, k∈ N}。

對第k個集合Ak平滑后的結果為：

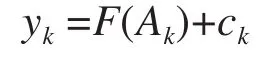
算法分析：

該算法多次運用了濾波算法的原理，對集合內部和集合之間分別進行了優化計算，不但能夠消除干擾項的影響，還能對評分基準進行平滑，讓最終結果在同一個基準上進行排序，使得考核結果更加真實有效。

2 實際應用分析

通過上述算法對績效考核分數進行去干擾項和平滑之后，能夠得到有效的考核結果。但是在實際應用中依然存在一些問題需要根據具體情況進行分析。

（1）對考核指標中的定量指標和定性指標需要單獨分開進行考慮，上述算法能夠適用于定性指標的分數糾偏，但由于定量指標有著更加量化的評分標準，其分數結果即使偏差較大，也不能作為干擾項去除，必須全部體現在考核結果中。

（2）在定性指標的打分結果中會存在誤認為是干擾項而被過濾的可能，有些偏差較大的分數也是評價結果的真實反映，單純按照過濾算法進行過濾，可能會把部分有效的數據剔除掉，從而影響結果的真實性。

（3）通過濾波算法糾偏之后，能夠消除不同集合間的差異性，但是如何盡可能地保留集合之間的差異性，體現各自集合的數據特點，這也是需要進一步研究的課題。

（4）考核結果的偏差性不僅僅受到算法的影響，更多的還是依賴于考核規則的設置是否合理，因此在研究如何體現績效考核的真實性和有效性時，也需要加強對考核規則本身的重視和思考。

3 結束語

綜上所述，利用復合濾波算法對考核結果進行糾偏，能夠去掉結果中的干擾項并平滑處理，結合企業的自身情況進行應用，可以獲得更準確的數據集，使企業的績效考核結果更加真實有效。

[1]黃才華. 企業績效考核體系中的問題與對策[J].河南師范大學學報（哲學社會科學版），2007，34（5）.

[2]焦振宇. 基于類民主評選規則的復合數字濾波法[J].中國儀器儀表，2004（12）：16-18.

[3]陳勁松，劉艷偉. 基于窗函數的FIR數字濾波器設計[J].制造業自動化，2012，34 （17）：104-105.