高效用項集挖掘算法

祝孔濤，李興建，王 樂

（1.南陽理工學院 軟件學院，河南 南陽473000；2.南陽理工學院 圖書館，河南 南陽473000；3.大連理工大學 創(chuàng)新實驗學院，遼寧 大連116624）

0 引 言

頻繁模式的挖掘僅僅考慮項集在多少個事務項集中出現(xiàn)，而沒有考慮項在一個事務中對應的數(shù)量和項的權重值，如在一個購物單中，同一個商品的購買的數(shù)量和商品的價格或利潤；但這些信息對于商務數(shù)據分析等應用卻很重要。針對該問題，提出了高效用項集的挖掘，并且也成為近來一個新的研究方向[1－9]，其研究的焦點主要是提高算法的時間和空間效率。

目前，高效用項集的挖掘算法主要采用兩階段方法[1－5，7，10，11]和項集枚舉[8，9]辦法。本文主要對基于兩階段方法的算法進行了研究；兩階段方法是指算法通過兩個階段來完成高效用項集的挖掘:候選項集挖掘和從候選項集中識別高效用項集。算法 CTU－Mine[11]針對 Two－Phase算法中的問題進行了改進，該算法采用樹結構的方式挖掘高效用項集，但是只在稠密數(shù)據集上的該算法的性能才優(yōu)于Two－Phase算法。算法IHUP[3]只需要兩次數(shù)據集掃描，并采用模式增長方式產生候選項集，候選項集的個數(shù)相對已有算法有了很大降低，算法的性能得到了較大的提高。算法 UP－Growth[1，4]針對IHUP算法提出了改進策略來降低候選項集個數(shù)。采用兩階段方式的算法主要問題就是產生候選項集過多，因此這會影響算法挖掘的時空效率。

針對此問題，本文從兩方面對算法UP－Growth進行改進，降低候選項集效用的估計值，從而減少候選項集的個數(shù)。實驗部分采用稀疏和稠密數(shù)據集進行了算法性能測試，實驗結果驗證了改進后算法的時間效率得到了較大的提高。

1 問題描述和相關定義

設數(shù)據集D＝｛t1，t2，t3，… ，tn｝共包含m個不同項，即I＝｛i1，i2，…，im｝，并且包含n個事務，其中tj（j＝1，2，3，…，n）表示D中第j個事務項集 （j被稱為事務項集的ID），事務項集tj可以表示為｛（x1:c1），（x2:c2），…，（xv:cv）｝，其中xk∈I（k＝1，2，...，v），ck是項xk在事務tj中的數(shù)量，記為q（xk，tj），ck也被稱為項xk的內部效用值，如表1中每個事務 （第二列）中的數(shù)值；項集I中每一項ir（1≤r≤m）的權重值記為p（ir），該權重值也被稱為項ir的外部效用值，如表2所示。｜D｜表示數(shù)據集的大小。

表1 帶效用數(shù)據的數(shù)據集實例

表2 利潤表實例

定義1 項x在事務t中的效用值，記為u（x，t），其定義如下

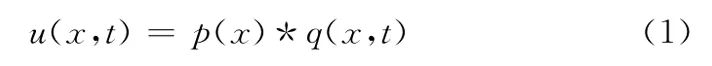
例如，在表中，u（b，T1）＝10＊3＝30。

定義2 項集X在事務t中的效用值，記為u（X，t），其定義如下

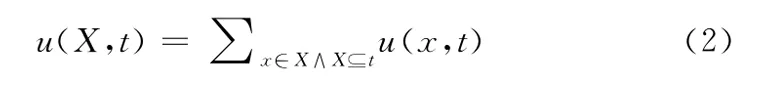
例如，在表中，u（｛bd｝，T1）＝u（b，T1）＋u（d，T1）＝30＋8＝38。

定義3 項集在一個數(shù)據集中的效用值:項集X在一個數(shù)據集Dut中的效用值，記為u（X），其定義如下

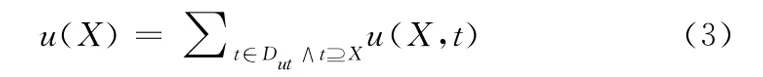
例如，在表中，u（｛bd｝）＝u（｛bd｝，T1）＋u（｛bd｝，T7）＝38＋46＝84。

定義4 一個事務t的效用值，記為tu（t），其定義如下

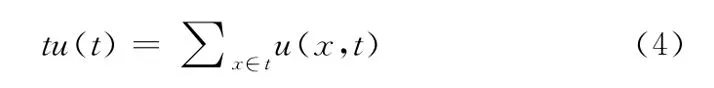
例如，在表中，tu（T3）＝u（d，T3）＋u（f，T3）＝24＋12＝36。

定義5 數(shù)據集總的效用值:一個數(shù)據集D的總效用值，記為Ttu（D），其定義如下

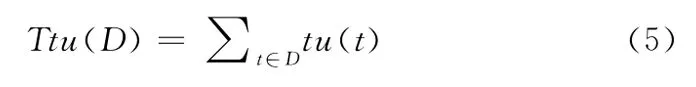
定義6 最小效用閾值η是用戶預定義的一個大于0小于1的值，在一個數(shù)據集Dut中，最小效用值min＿uti定義如下

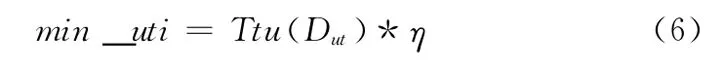
定義7 在一個數(shù)據集中，一個項集的效用值不小于預定義的最小效用值，則該項集就成為一個高效用項集。

定義8 項集的事務權重效用值 （transaction－weightedutilization，twu）:在一個數(shù)據集Dut中，一個項集X的事務權重效用值，記twu（X）為，定義如下

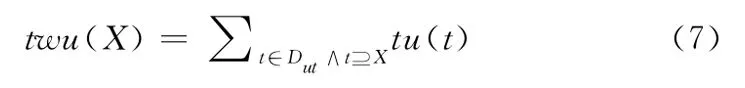
其是包含該項集的所有事務效用值的和，例如，twu（｛bd｝）＝tu（T1）＋tu（T7）＝50＋54＝104。

定義9 高效用項集的候選項集與非候選項集:一個項集／項X的twu值不小于預定義的最小效用值，則該項集／項就是一個候選項集／項，否則就是非候選項集／項。

性質項集的事務權重效用值滿足閉包屬性[12]:任一個候選項集的非空子集也是一個候選項集，任一個非候選項集的超集也是一個非候選項集。

2 算法設計

UP－Growth和IHUP[3]在計算項的twu值的時候，將低效用值的項和已經被處理過的項對應的效用值都計算到相關項集的twu值中，因此當處理到頭表中一項的時候，可以重新計算該項的twu值，如果新計算的twu值小于預定義的最小效用值，則就不需要再繼續(xù)為該項創(chuàng)建子頭表和子樹。另外本文還利用項在事務中的最大效用值和最小效用值來降低項集被估計的效用值，從而可以將少候選項集、以及挖掘過程中創(chuàng)建樹的棵數(shù)。本文將以上策略應用到UP－Growth中進行算法改進，將改進后算法記為IUPGrowth；另外以上的策略可以應用到所有采用模式增長方式的算法中來降低候選項集的個數(shù)。

IUP－Growth主要包括兩個過程:創(chuàng)建樹UP－Tree和從樹上挖掘高效用模式，其中從樹上挖掘高效用模式是一個遞歸的過程，在這個過程中需要遞歸的創(chuàng)建新的子樹、以及從新的子樹上再遞歸的執(zhí)行模式挖掘。

（1）創(chuàng)建樹 UP－Tree

這里創(chuàng)建UP－Tree的方法和算法UP－Tree中創(chuàng)建樹的方法相同，以表1和表2中數(shù)據為例說明UP－Tree的構建，這里設定最小效用值為80。

在第一遍數(shù)據集的掃描中，統(tǒng)計出每項的支持數(shù) （sn）和事務權重效用值 （twu），然后只保留twu值不小于80的項，并且按支持數(shù)從大到小排序，如圖1（a）所示，其中頭表中還記錄link（為了使圖清晰，圖中表示link的線沒畫）。

在第二遍數(shù)據集掃描中，主要任務就是將每個事務項集添加到一棵樹上，每個事務項集添加到樹上的步驟如下:①將事務項集中不在頭表中的項刪除；②事務項集中剩余項按頭表的順序排序；③將排好序的事務項集添加到樹上。

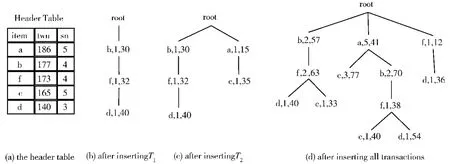
圖1 UP－Tree的構造 （最小效用值為80）

例如表1中第一個事務，按以上步驟中的 （1）和 （2）中方法處理后得到事務項集為｛（b，10）（f，1）（d，1）｝；然后將事務項集添加到一棵樹上，如圖1（b）所示，其中每個節(jié)點上的第一個數(shù)值表示該節(jié)點的支持數(shù)，第二個數(shù)值是節(jié)點及祖先節(jié)點效用值的和，如節(jié)點 “b”上的 “30”是節(jié)點 “b”的效用值，節(jié)點 “f”上的 “32”是節(jié)點 “b”和 “f”的效用值的和，節(jié)點 “d”上的 “30”是節(jié)點 “b”、“f”和 “d”的效用值的和。圖1（c）是添加前兩個事務項集后的結果；圖1（d）是添加表1中所有數(shù)據后的結果。

在數(shù)據集的第二遍掃描過程中，算法IUP－Growth還統(tǒng)計了各項在事務中的最大以及最小效用值，如表3所示，該表記為項最大 ＆最小效用值表 （minimum ＆maximum item utility table，MMUT）。表3中數(shù)據用來降低候選項集的twu值，從而可以減少候選項集的個數(shù)，即用來候選項集的剪枝，詳見頻繁模式挖掘過程。

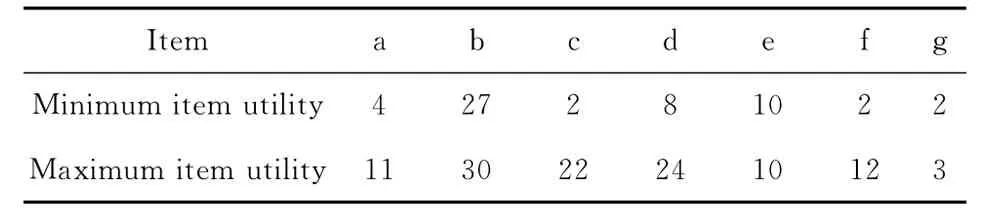
表3 項最小與最大效用表 （MMUT）

（2）從樹上挖掘高效用模式

算法IUP－Growth從樹上挖掘高效用模式的算法首先是從頭表的最后一項開始處理，其中每項的處理步驟如下（假設當前正在處理的UP－tree樹記為T，當前正在處理的頭表為H，當前正在處理的項為Y）:

步驟1 在頭表H中，Y.link中記錄了樹UP－tree上所有節(jié)點Y，設為k個節(jié)點N1，N2，…，Nk；

步驟2 計算k個節(jié)點上utility的和，記new＿twu＝；如果new＿twu小于最小效用值，則執(zhí)行步驟11；否則執(zhí)行下一步；

步驟3 將項Y添加到一個基項集base－itemset（初始值為空）；

步驟4 通過掃描樹T上包含節(jié)點Y到根節(jié)點的所有枝，為基項集｛Y｝創(chuàng)建一個子頭表subH，子頭表中包含所有對應的候選及非候選項；

步驟5 計算基項集的最大效用值 （記為BIMU），即項集中各項最大效用值與項Y的支持數(shù)的乘積的總和，如果BIMU小于預定義的最小效用值，則執(zhí)行步驟10。

步驟6 計算子頭表subH中所有項的最小效用值的和（記為MTU），其中每項的最小效用值等于項最大＆最小效用值表中最小效用值與該項在子頭表中支持數(shù)的乘積；

步驟7 如果new＿twu–mtu的差不小于最小效用值，則將當前基項集添加到候選項集集合中；

步驟8 刪除子頭表中twu值小于最小效用值的項，剩余項按支持數(shù)從大到小排序；

步驟9 如果子頭表不為空，則再次掃描樹T上包含節(jié)點Y到根節(jié)點的所有枝，為當前基項集創(chuàng)建條件樹，然后按照處理頭表H的方法遞歸的處理子頭表subH；

步驟10 從基項集base－itemset中刪除項Y；

步驟11 按照處理頭表H中項Y的方法，處理頭表H中下一項。

算法IUP－Growth和算法 UP－Growth的主要區(qū)別:UP－Growth會將頭表中每一項添加到基項集base－itemset中，而每產生一個新的基項集都是一個候選項集，而算法IUP－Growth會在步驟2中重新計算項的twu值，而新計算的值不包含事務項集中刪除項的效用值和已經被處理的項的效用值；同時算法IUP－Growth中步驟5－7，其包含2個判斷條件來減少候選項集的個數(shù)，從而提高算法的處理效率。

IUP－Growth從樹上挖掘候選項集的算法如圖2所示。IUP－Growth從樹上挖掘到候選項集后，最后再掃描一遍數(shù)據集來統(tǒng)計各個候選項集真實的效用值，當真實的效用值不小于最小效用值，則該候選項集就是一個高效用項集。

圖2 挖掘候選項集算法

下面通過一個例子來說明IUP－Growth的挖掘過程，例如當處理圖1（a）中的項 “d”時，處理步驟如下:

步驟1 計算項 “d”新的twu值，即new＿twu＝40＋54＋36＝130，因為new＿twu值不小于80，則執(zhí)行下一步，否則就不需要繼續(xù)處理該項；

步驟2 將項 “d”添加到基項集base－itemset中；

步驟3 計算項集base－itemset中所有項的最大效用值和，即BIMU＝24＊3＝72，因為BIMU的值小于最小效用值，則該項集不是一個候選項集；

步驟4 因為new＿twu值大于最小效用值，則通過掃描樹T（圖1（d））上包含節(jié)點 “d”到根節(jié)點的所有枝，為當前基項集創(chuàng)建子頭表，如圖3（a）所示 （因為步驟3中已經判斷基項集不是一個候選項集，則這里的子頭表也不需要再保存twu值小于最小效用值的項）；

步驟5 因為新建子頭表不為空，所以需要為當前基項集創(chuàng)建條件樹，例如圖3（a）中的樹；

步驟6 遞歸的處理新的子頭表中的每一項，例如處理子頭表中的項 “b”，得到項集｛db｝的子頭表和子樹，如圖3（b）所示；得到和項 “d”相關的候選項集有｛db｝和｛dbf｝。

圖3 挖掘高效用項集的例子

步驟7 處理完子頭表中的每一項，繼續(xù)處理圖1（a）中項 “d”的下一項 “c”，如圖3 （c）是項集 “c”的子頭表和條件樹；從新的子樹中可以得到新的候選項集｛ca｝；

步驟8 處理圖1（a）中頭表的下一項 “f”，為項集｛f｝創(chuàng)建的子頭表和樹如圖3（d）所示；得到和項 “f”相關的候選項集有｛fb｝；

步驟9 處理圖1（a）中頭表的下一項 “b”，沒有新的子樹產生；得到新的候選項集有｛b｝；

步驟10 處理圖1（a）中頭表的下一項 “a”，沒有新的子樹產生；得到新的候選項集有｛a｝。

3 實 驗

實驗平臺:Windows 7操作系統(tǒng)，4G內存 （實際可用2.99G），Intel（R）Core（TM）i5－2300CPU ＠2.80GHz；Java堆空間設置為1.5G。將改進后的算法IUP－Growth和UPGrowth挖掘的結果相同，都能將所有的高效用項集挖掘出來，因此這里僅進行了算法時間性能對比，實驗對比算法都是采用Java編程語言實現(xiàn)。測試數(shù)據3個:Chain－store[13]、mushroom[14]和 T10.I6.D100K，其中 T10.I6.D100K是一個用IBM數(shù)據生成器[15]合成的數(shù)據集。Chain－store是California一家鏈鎖超市產生的真實數(shù)據[13]；數(shù)據集mushroom和T10.I6.D100K中沒有提供數(shù)據的內部效用值和外部效用值，本文采用文獻[3，10－12]中方法，事務項集中項的個數(shù)（內部效用值）采用隨機的方法產生一個小于10大于0的整數(shù)；項的單位效用值 （外部效用值）也是隨機產生一個數(shù)值 （大于等于0.0100，小于等于10.0000）。

表5 數(shù)據集T10.I6.D100K的高效用項集和候選項集個數(shù)

表6 數(shù)據集chain－store的高效用項集和候選項集個數(shù)

表4～表6是3個數(shù)據集在不同的最小效用閾值下包含的高效用項集個數(shù)、以及兩個算法產生的候選項集個數(shù)，表中第二行是IUP－Growth算法在不同的閾值下產生的候選項集個數(shù)，第三行是UP－Growth算法在不同的閾值下產生的候選項集個數(shù)。從這3個表中很容易看出IUP－Growth算法產生的候選項集個數(shù)明顯低于算法UP－Growth，特別在真實數(shù)據集chain－store上更為明顯，因此這會導致算法IUP－Growth的時間和空間性能優(yōu)于算法UP－Growth，正如實驗結果圖4～圖6所示，算法IUP－Growth的運行時間明顯低于 UP－Growth，在真實數(shù)據集chain－store上，IUPGrowth算法性能優(yōu)勢更為明顯；另圖6中當閾值取0.03%的時候，算法UP－Growth發(fā)生內存溢出。

在圖5（a）的實驗中，當閾值從0.2%降低到0.1%的時候，數(shù)據集T10.I6.D100K中的高效用項集個數(shù)由131上升到524個，同時兩個算法產生的候選項集個數(shù)增加的也比較快，如表5所示，所以在這種情況下，算法的運行時間也會相應增加比較快。

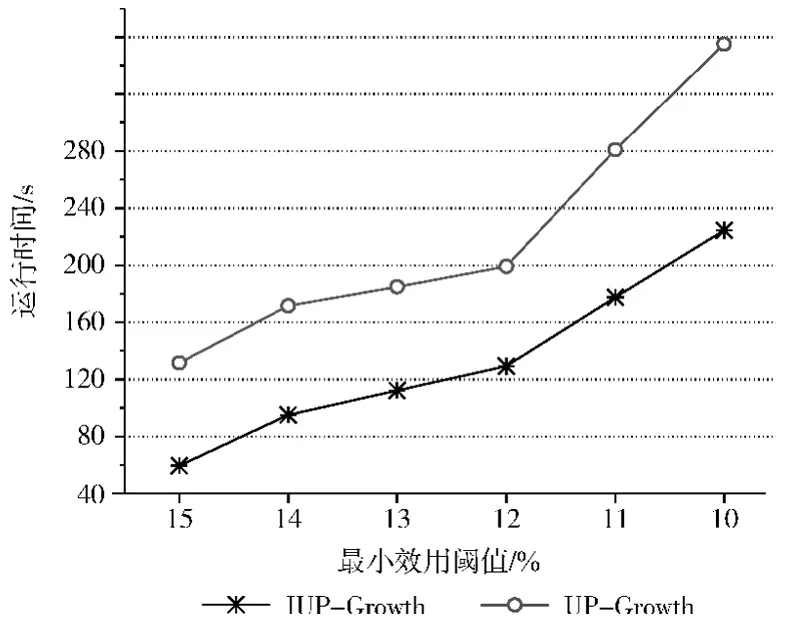
圖4 數(shù)據集mushroom實驗數(shù)據對比

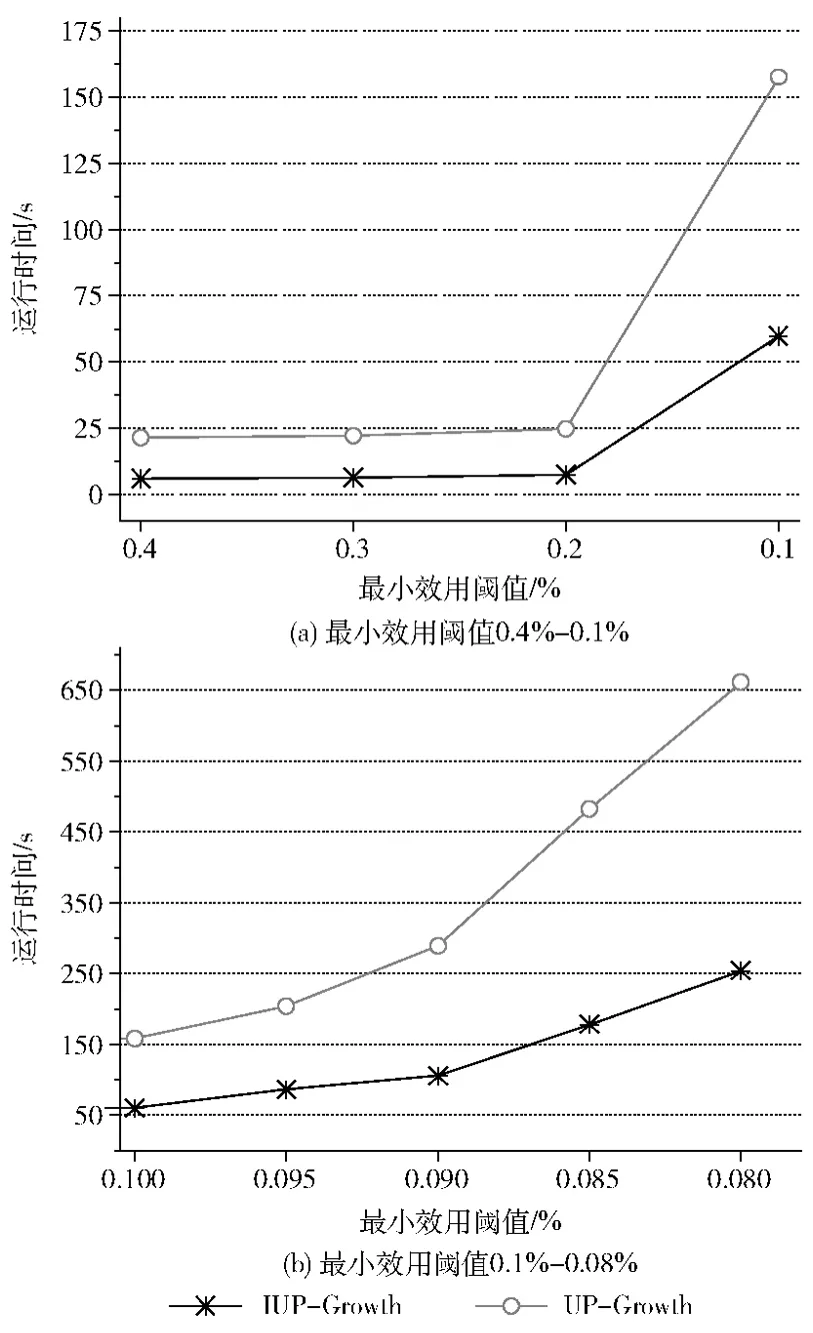
圖5 數(shù)據集T10.I6.D100K實驗數(shù)據對比

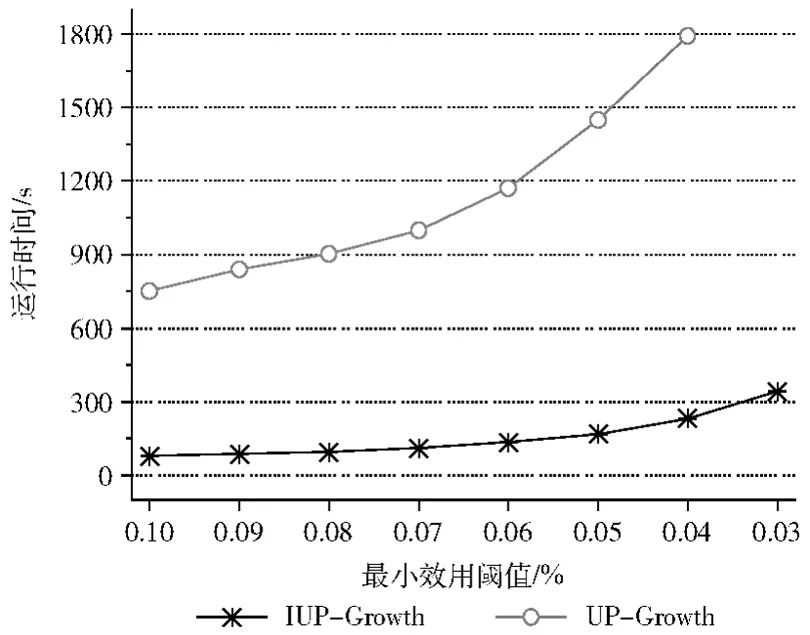
圖6 數(shù)據集chain－store實驗數(shù)據對比

4 結束語

本文通過對兩階段法高效用項集挖掘算法的研究，為有效剪枝候選項集，提出了改進策略:在不影響項集效用值的基礎上，降低候選項集的twu值，從而減少候選項集個數(shù)；另外通過項的最大和最小效用值來估計候選項集的效用值，這個策略也可以有效的減少候選項集的個數(shù)。實驗采用了3個典型數(shù)據集，包括真實數(shù)據集和合成數(shù)據集；實驗結果也表明了本文提出的策略在保證正確的挖掘結果的條件下，能有效地減少了候選項集的產生，從而算法的時間和空間性能得到了較大的提高，特別是在真實數(shù)據集上表現(xiàn)更為出色。

[1]Tseng V S，Shie B，Wu C，et al.Efficient algorithms for mining high utility itemsets from transactional databases[J].IEEE Transactions on Knowledge and Data Engineering，2012 （1）:1－10.

[2]Li H，Huang H，Chen Y，et al.Fast and memory efficient mining of high utility itemsets in data streams[C]／／Maui，HI，United States:Association for Computing Machinery，2008.

[3]Ahmed C F，Tanbeer S K，Jeong B S，et al.Efficient tree structures for high utility pattern mining in incremental databases[J].IEEE Transactions on Knowledge and Data Engineering，2009，21 （12）:1708－1721.

[4]Tseng V S，Wu C W，Shie B E，et al.UP－Growth:An efficient algorithm for high utility itemset mining[C]／／ Washington，DC，United States，2010.

[5]Lin C W，Hong T P，Lan G C，et al.Mining high utility itemsets based on the pre－large concept[M].Advances in Intelligent Systems and Applications，2013:243－250.

[6]Song W，Liu Y，Li J.Vertical mining for high utility itemsets[C]／／ Maui，HI，United States:Association for Computing Machinery，2012.

[7]Wu C W，Shie B，Tseng V S，et al.Mining top－K high utility itemsets[C]／／Washington，DC，United States，2012.

[8]Liu J，Wang K，F(xiàn)ung B.Direct discovery of high utility itemsets without candidate generation[C]／／ Maui，HI，United states:Association for Computing Machinery，2012.

[9]Liu M，Qu J.Mining high utility itemsets without candidate generation[C]／／ Maui，HI，United states:Association for Computing Machinery，2012.

[10]Li Y C，Yeh J S，Chang C C.Isolated items discarding strategy for discovering high utility itemsets[J].Data and Knowledge Engineering，2008，64 （1）:198－217.

[11]Erwin A，Gopalan R P，Achuthan N R.CTU－mine:An efficient high utility itemset mining algorithm using the pattern growth approach[C]／／IEEE Computer Society Washington，2007.

[12]Liu Y，Liao W K，Choudhary A.A two－phase algorithm for fast discovery of high utility itemsets[C]／／ Hanoi，Viet nam:2005.

[13]Pisharath J，Liu Y，Ozisikyilmaz B，et al.NU－MineBench version 2.0source code and datasets[EB／OL].http:／／cucis.ece.northwestern.edu／projects／DMS／MineBench.html，2012.

[14]Goethals B.Frequent itemset mining dataset repository[EB／OL].http:／／fimi.cs.helsinki.fi／data／.Frequent itemset mining dataset repository，2010.

[15]IBM data generator[EB／OL].http:／／www.almaden.ibm.com／software／quest／Resources／index.shtml，2012.