臨床試驗中生存分析的非劣效研究設計及R軟件實現*
哈爾濱醫科大學衛生統計教研室(150081) 吳 瑩 侯 艷 李 康
近年,非劣效性臨床試驗在藥品開發中已有廣泛的應用,統計學上關于試驗藥物相對于陽性對照藥物的非劣效性評價方法已有多種,但主要集中在終點指標為二分類或正態連續型數據的臨床試驗〔1〕。當觀察指標為生存時間(survival time)時,可能包含截尾數據(censored data),則缺少相應的非劣效性評價方法,主要原因是生存分析設計背景下非劣效性的定義較為困難〔2〕。本文擬介紹一種基于生存時間指數分布模型,假設對照組死亡風險率λ0與試驗組死亡風險率λ1之比為常數ρ,并在此基礎上定義非劣效界值的分析方法,結合實例介紹其試驗設計和統計檢驗方法,同時給出R軟件實現程序。
非劣效界值的確定
假設研究計劃用T年時間納入病例,每位病例入組后均進行βρ年的隨訪觀察,則基于指數分布的生存分析模型需作以下假定〔3〕:
(1)單位時間內患者的入組人數服從泊松分布,年入組率記為A人/年;
(2)病例從入組到發生失效事件(failure event)所經歷的時間(生存時間)服從指數分布,其中陽性對照組的中位數記為M0,試驗組的記為M1,則相應的死亡風險率(hazard rate)為 λi=(ln2)/Mi,i=0,1。
(3)病例從入組到失訪,即產生截尾值(censored value)所經歷的時間相互獨立并服從指數分布,其中陽性對照組的失訪率記為φ0,試驗組的記為φ1。
為敘述簡單,本文假定時間單位為年,在實際應用中可選擇任意合適的時間單位。現令ρ=λ0/λ1=M1/M0,由于中位生存時間越長表示療效越好,可將非劣效界值定義為ρ1(ρ1≤1),它代表臨床上可接受的試驗藥療效遜于陽性對照藥的程度〔4〕。
假設檢驗與統計推斷
針對上述非劣效界值ρ1,假設檢驗形式為
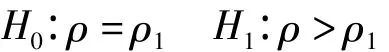
設第i(i=0,1)組病例觀察到的失效事件數為Di,總的觀察時間為Ti(暴露人年數),則λi的極大似然估計為^=Di/Ti。令,Bristol〔5〕提出統計量

近似服從標準正態分布,當 Z≥Z1-α時拒絕 H0,Z1-α為標準正態分布的1-α分位數,S(λ0,λ1)為lnρ的標準差估計值,即
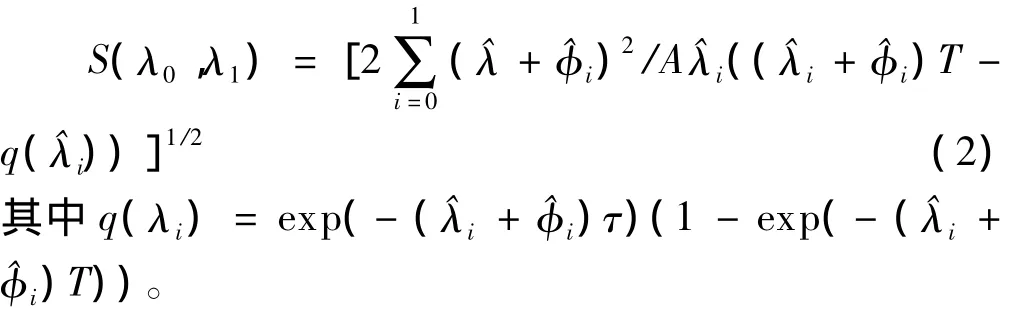
檢驗效能與入組時間
生存分析的非劣效性檢驗在設計時一般不直接估計樣本含量,而是根據平均年入組人數估計達到一定檢驗效能所需入組時間T,或者直接估計所需陽性事件數。下面給出基于入組時間的檢驗效能函數

ρ=ρ1時表示 H0成立,power=α;ρ=ρ2>ρ1時,(3)式表示正確接受H1的概率即檢驗效能。受疾病發病率及試驗設計等因素影響,不同生存分析研究的單位時間內入組人數A不同,因此其樣本含量大小取決于納入患者的時間長度,即入組時間T,當要求檢驗效能達到1-β 時,Bristol〔5〕提出所需入組時間 T應滿足
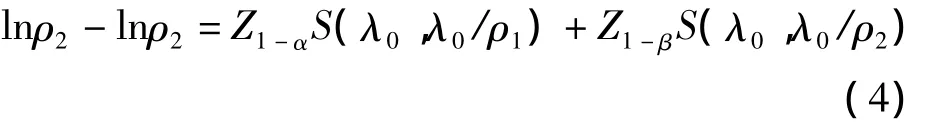
其中Z1-α和 Z1-β分別代表標準正態分布 1- α、1-β 的分位數,S(λ0,λ0/ρ1)和 S(λ0,λ0/ρ2)分別代表(2)式中 λ1= λ0/ρ1和 λ1= λ0/ρ2的情況。按上述理論方法編寫的R軟件實現程序見附錄,輸入不同參數設置值即可返回不同情況下所需入組時間。
實 例
欲考察某一新型放療方法與傳統療法相比,對非小細胞肺癌患者的治療效果是否具有非劣效性,主要指標為5年生存率,查閱相關文獻及數據,假定陽性對照組中位生存時間為2.78年,當檢驗水準α=0.05,檢驗效能1-β=80%或90%時,根據本文方法,表1給出當非劣效界值 ρ1=0.8或0.9,失訪率 φ0=φ1=0.06或0.01,H成立時兩組死亡風險率之比ρ2=1.0或1.25,年入組人數A=20、30、40或50時所需入組時間T。
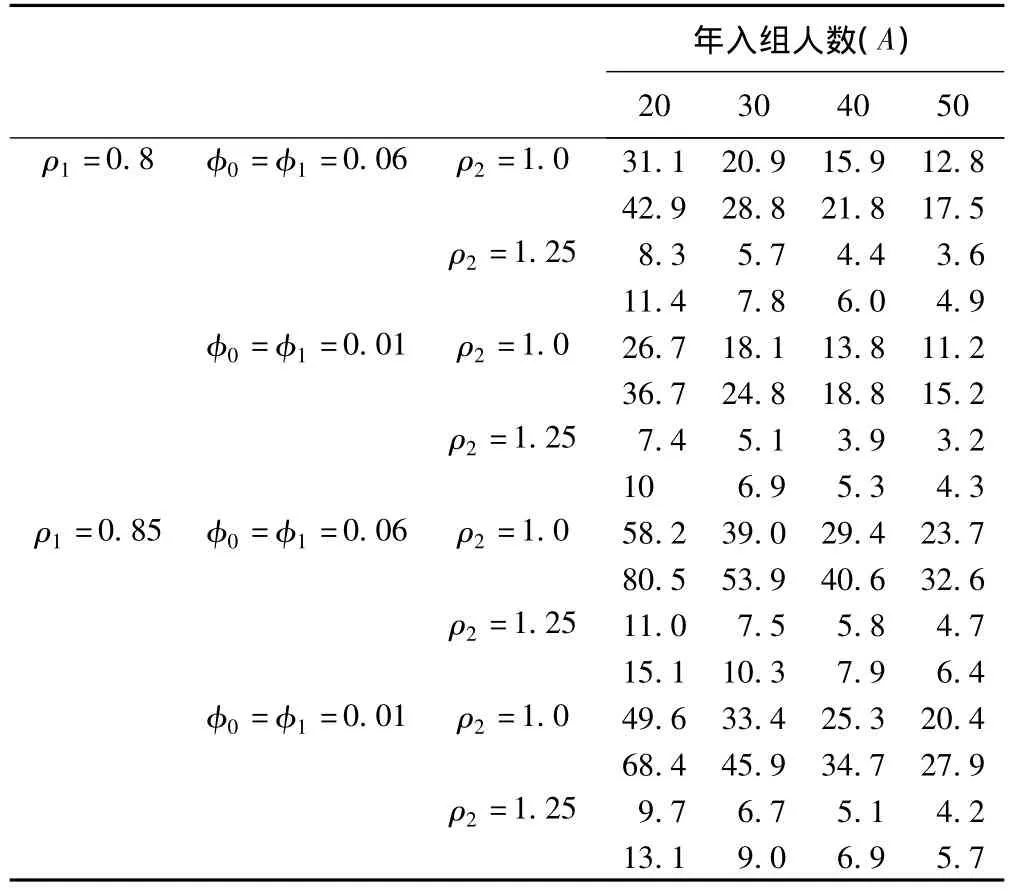
表1 不同試驗條件下所需入組時間(T)
由表1可以看出,非劣效界值ρ1定義越大或者檢驗效能1-β要求越高,所需入組時間越長,而試驗組相對療效ρ2越高,年入組人數A越多或者失訪率φ越低,所需入組T時間則越短,這與理論推導結果一致。在應用時研究者可以結合臨床實際選擇合適的參數配置進行試驗。
小結與討論
本文介紹了一種基于生存時間指數分布模型的非劣效性試驗設計及統計推斷方法。在介紹Bristol方法原理的基礎上,結合實例探討了如何計算試驗入組時間以達到預計檢驗效能,并給出了R軟件實現程序。實例結果表明,在其他條件一致的基礎上,生存時間數據的非劣效設計所需入組時間與檢驗效能、非劣效性界值、年入組率及失訪率有關。Bristol方法適用于生存分析中包含截尾值的非劣效研究的臨床試驗設計和統計分析。
基于指數分布模型的生存時間數據統計分析方法,提供了在安慰劑對照面臨醫學倫理問題,或陽性對照藥物雖療效略好于試驗藥,但在不良反應、藥物成本等其他方面存在劣勢時〔6〕,非劣效性設計的評價方法。對于同類型的試驗設計,Stallard〔7〕等人亦提出了基于Weibull分布的參數評價方法,但其抽樣方案僅限于動物致癌性數據,不適合應用于臨床試驗。此外,亦有學者提出了利用生存時間順序統計量的非參數評價方法〔8-9〕,與本文介紹的參數方法相比,雖然損失了一定的樣本信息,但適用于任意數據分布形式,因此在實際應用中需具體考察數據分布特征,選擇合適的分析方法。



1.Freitag G.Methods for assessing noninferiority with censored data.Biometrical Journal,2005,47(1):88-98.
2.Fleming TR.Current issues in non-inferiority trials.Statistics in Medicine,2008,27:317-332.
3.Rubinstein LV,Gail MH,Santner TJ.Planning the duration of a comparative clinical trial with loss to follow-up and a period of continued observation.J Chron Dis,34:469-479.
4.Com-Nougue C,Rodary C,Patte C.How to establish equivalence when data are censored:a randomized trial of treatments for n non-hodgkin lymphoma.Statistics in Medicine,1993,12:1353-1364.
5.Bristol DR.Planning survival studies to compare a treatment to an active control.Journal of Biopharmaceutical Statistics,1993,3(2):153-158.
6.D'Agostino SRB.Non-inferiority trials:advances in concepts and methodology.Statistics in Medicine,2003,22:165-167.
7.Stallard N,Whitehead A.An alternative approach to the analysis of animal carcinogenicity studies.Regulatory Toxicology and Pharmacology,1996,23:244-248.
8.Freitag G,Lange S,Munk A.Non-parametric assessment of non-inferiority with censored data.Statistics in Medicine,2006,25:1201-1217.
9.Tangen CM,Koch GG.Non-parametric covariance methods for incidence density analyses of time-to-event data from a randomized clinical trial and their complementary roles to proportional hazards regression.Statistics in Medicine,2000,19:1039-1058.

