實時快速NURBS直接插補技術

王國勛 王宛山 王 軍 舒啟林

1.東北大學，沈陽，110819 2.沈陽理工大學，沈陽，110159

0 引言

傳統數控系統只支持直線插補和圓弧插補，在加工復雜曲線時，先將曲線用很多段小直線段或圓弧段近似，然后再進行直線插補或圓弧插補，這種方法在高速加工中會帶來許多問題：①刀具進給方向快速突變，加速度及加加速度過大，容易導致過沖和振動，從而影響表面質量和加工精度，為了保證表面質量和加工精度，必須降低進給速度［1］；②只針對小線段進行速度規劃，在小線段的起點和終點頻繁進行加減速，嚴重影響加工效率，不易實現高速加工；③程序文件龐大，增加了CAD／CAM與CNC之間的數據傳輸負擔。

為了克服傳統插補方法的缺點，許多現代CAD／CAM系統開始使用曲線參數描述方法和參數曲線插補技術。非均勻有理B樣條曲線（NURBS）由于具有諸多優點而獲得廣泛應用。另外，NURBS已成為STEP-NC標準中自由曲線曲面唯一的表示形式，即NURBS的應用擴展至CNC領域，CAD／CAM與CNC的數據描述實現了統一。因此，研究直接NURBS插補技術，有利于更有效地利用CAD系統的數據。研究表明，相比直線、圓弧插補技術，直接NURBS插補技術可獲得更高的表面質量和效率［2］。

許多研究人員對NURBS插補技術進行了深入的研究。大多數直接插補算法試圖用泰勒展開法近似表示進給步長和參數增量之間的關系，Yeh等［3］用一階泰勒展開式研究了插補算法，提出了自適應插補算法，在保證輪廓誤差的前提下根據曲率調節速度；趙國勇等［4］基于二階泰勒展開式提出了插補算法，以獲得更高的精度。但應用泰勒展開式研究插補算法時忽略了高階項，因此存在累積截斷誤差，造成實際進給速度與給定速度不一致，存在速度波動。為了解決這個問題，必須對下一插補點的參數值進行誤差補償，Tsai等［5］設計了一種參數曲面曲線“預測-修正”插補器，根據給定的速度誤差迭代修正下一插補點參數值，直到滿足誤差要求為止。此方法能有效地減小速度波動，但是插補過程中需要進行迭代計算，影響插補實時性，如果某次迭代時間超過插補周期，將打亂插補過程。

本文根據插補原理，運用NURBS直接插補思想，研究了NURBS快速直接插補算法。為了滿足插補精度的要求，插補速度可根據弓高誤差限定值自適應調整。

1 NURBS曲線描述

一條k次NURBS曲線可以表示為一分段有理多項式矢函數［6］：

其中，ωi（i＝0，1，…，n）稱為權因子，分別與控制頂點di相聯系；Ni，k（u）是k次規范B樣條基，由節點矢量U ＝ （u0，u1，…，un＋k＋1）決定，通常由De Boor-Cox遞推公式定義。

2 目前的NURBS曲線插補方法

目前大多數NURBS插補方法都是基于泰勒展開式的，即用泰勒展開式近似求取下一插補點的參數值，常用的有一階泰勒展開式和二階泰勒展開式。插補計算公式如下。

一階泰勒展開式：

二階泰勒展開式：

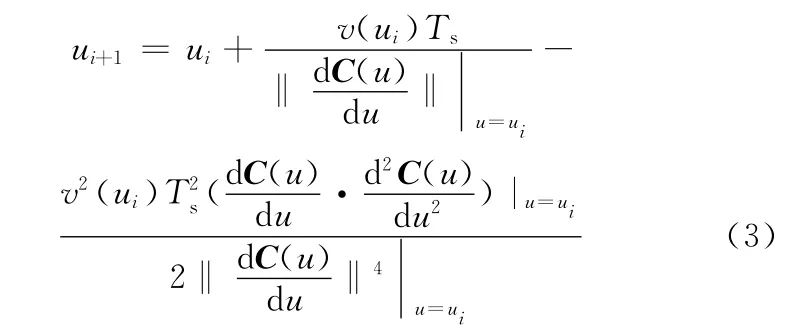
由式（2）、式（3）可發現，泰勒公式展開法插補計算忽略了高階項，致使進給速度發生變化，增大了弓高誤差［7］。如圖1所示，下一個插補點參數理論值為ui＋1，對應的弦長為ΔLi，而利用泰勒公式法計算得到的下一插補點參數值為u′i＋1，對應的弦長為ΔL′i，由于u′i＋1＜ui＋1，所以ΔL′i＜ΔLi，而插補周期為定值，所以實際插補進給速度小于給定速度，產生速度波動。另外，計算插補速度時是按照曲線弧長對時間導數求取的，而根據插補原理，刀具實際路徑為弦長，而非弧長，如圖2所示，插補時刀具實際走過的路徑為弦長ΔLi，而不是弧長ΔSi，因此，使用泰勒公式展開法進行插補計算，存在速度波動問題。本文根據插補原理，基于進給速度求取下一插補點插補參數增量Δui來解決這一問題。

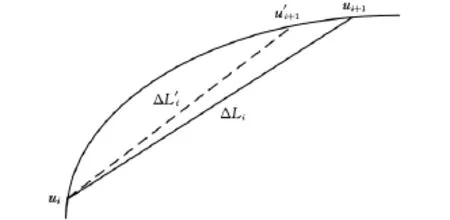
圖1 泰勒展開式插補算法

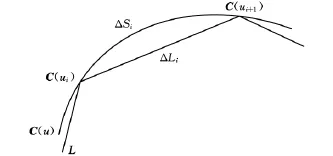
圖2 NURBS曲線插補原理圖

3 插補算法

3.1 插補計算過程

假設NURBS曲線C（u）在定義域中連續并且二階可導，曲率半徑ρ（u）存在并連續，且曲線上任意插補點滿足max｜ΔLi｜?ρi。根據插補原理，可求得插補計算公式［8］：

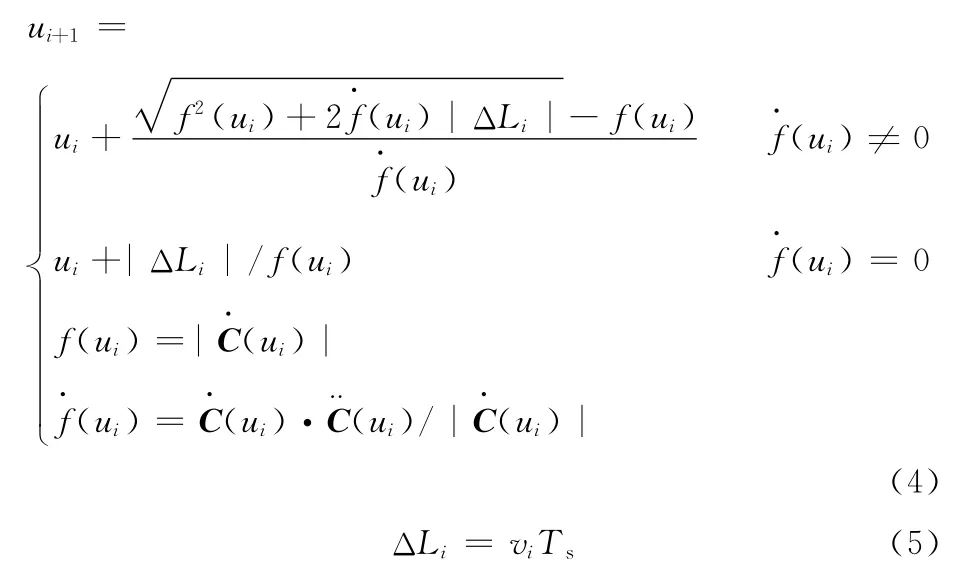
其中，ΔLi為插補弦長（步長），vi為給定進給速度，由式（4）、式（5）可知，下一插補點參數值ui＋1由進給速度vi決定，有效地減小了進給速度的波動。

3.2 特殊點處理

如果k次NURBS曲線內節點重復度為k，則曲線在該點處形成一個尖點，如圖3所示。

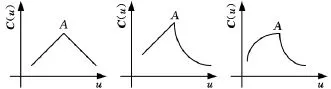
圖3 NURBS曲線上的尖點

通常，在尖點區域加速度和加加速度容易超過機床最大允許值，不利于高速、高精度加工，為了解決這個問題，Shen等［9］提出了一種二維NURBS曲線的插補算法，將曲線在尖點處分段，然后在每個分段上進行插補，在加工尖點區域前必須進行減速，在每個尖點處速度都要減到零，下一段曲線插補速度從零開始加速，這樣避免了尖點處的加速度和加加速度突變，但卻降低了加工效率。又因為曲線在尖點處不存在二階導數，因此本文的插補算法在尖點處不適用，為了保持整條曲線插補的連續性，提高加工效率，必須對尖點處曲線進行處理。本文將尖點處曲線在允許的誤差范圍內進行近似插值，使其變光滑，且二階可導，保持插補的連續性，提高加工效率。具體方法如下。

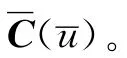
4 NURBS快速計算方法

由以上分析可知，在NURBS插補計算過程中，需要進行NURBS求值、求導的計算。對于NURBS曲線的計算主要是對非均勻B樣條基的計算，一般采用de Boor遞推算法［10］進行計算，但是每一次計算都要重復算法中的遞歸調用過程和計算過程，影響效率。對于求導計算，NURBS曲線的定義式（1）是有理分式，對NURBS曲線直接求導非常復雜，分母會出現高次冪，因此，研究NURBS的快速計算法對于插補算法具有重要意義。NURBS曲線是以非均勻B樣條為基礎的樣條曲線，因此可以轉換為矩陣表示，與常規表示方法比較，矩陣表示法求值求導效率高。

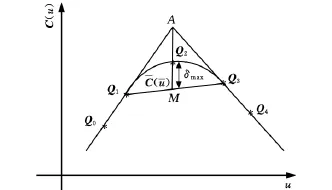
圖4 尖點處的NURBS插值

4.1 NURBS快速求值算法

根據B樣條基函數性質得到，當u∈ ［ui，ui＋1］時，NURBS曲線可表示成矩陣形式：

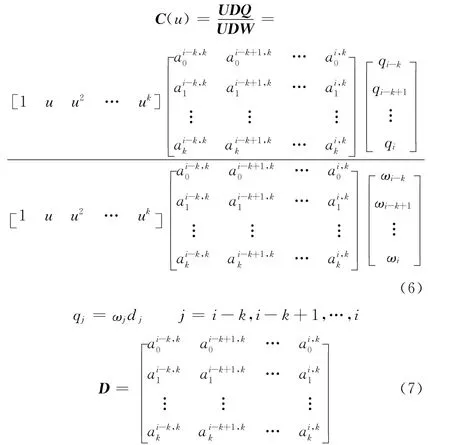
只需求出系數矩陣D，即可計算曲線C（u），因此，研究系數矩陣D的直接遞推法對于NURBS的計算具有實際意義。de Boor［11］給出了B樣條的導數公式：

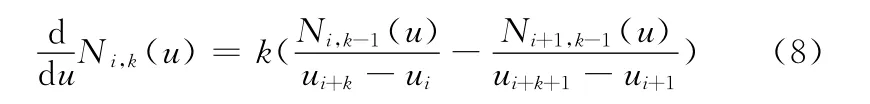
在遞推過程中還要滿足函數的連續條件：

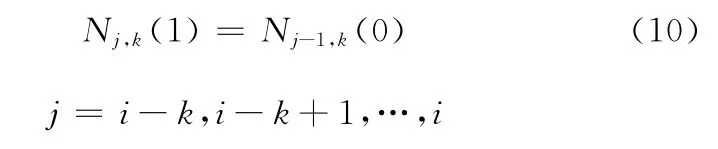
于是，每積分遞推式（9）中第二式一次，可得到高一次的非均勻B樣條基函數，經過逐次積分便可遞推出任意次非均勻B樣條基函數。式（9）中第二式左端積分后的結果為Nj，k（u），其多項式表示為

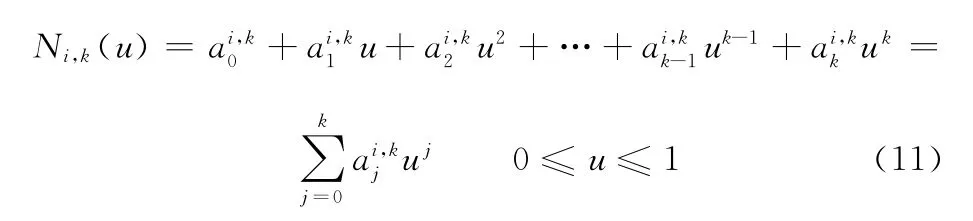
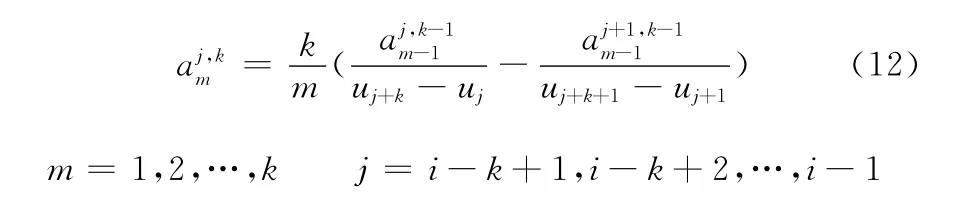
根據非均勻B樣條的性質，當u∈ ［ui，ui＋1］時，有

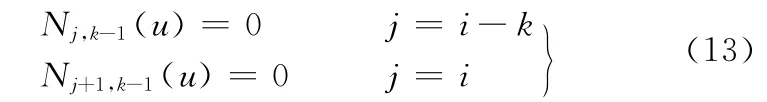
因此

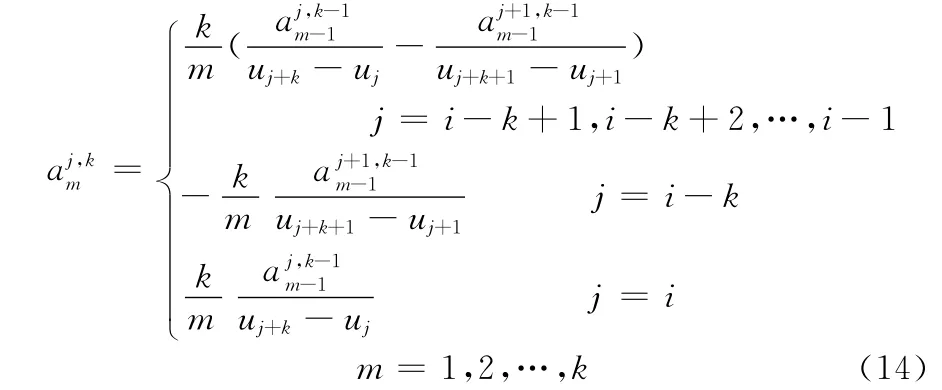
由式（10）得

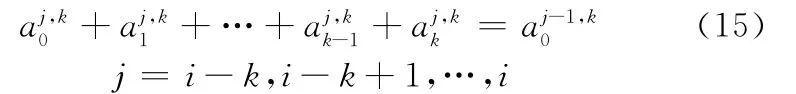
由非均勻B樣條的性質，可得j＝i-k時有

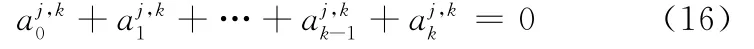
因此得

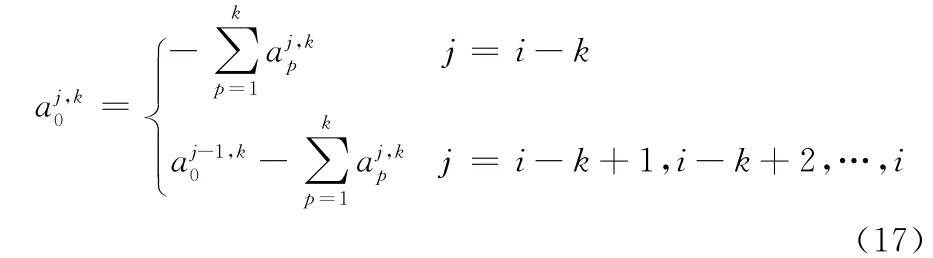
綜合式（14）和式（17）可得，系數矩陣D全部元素的遞推公式為

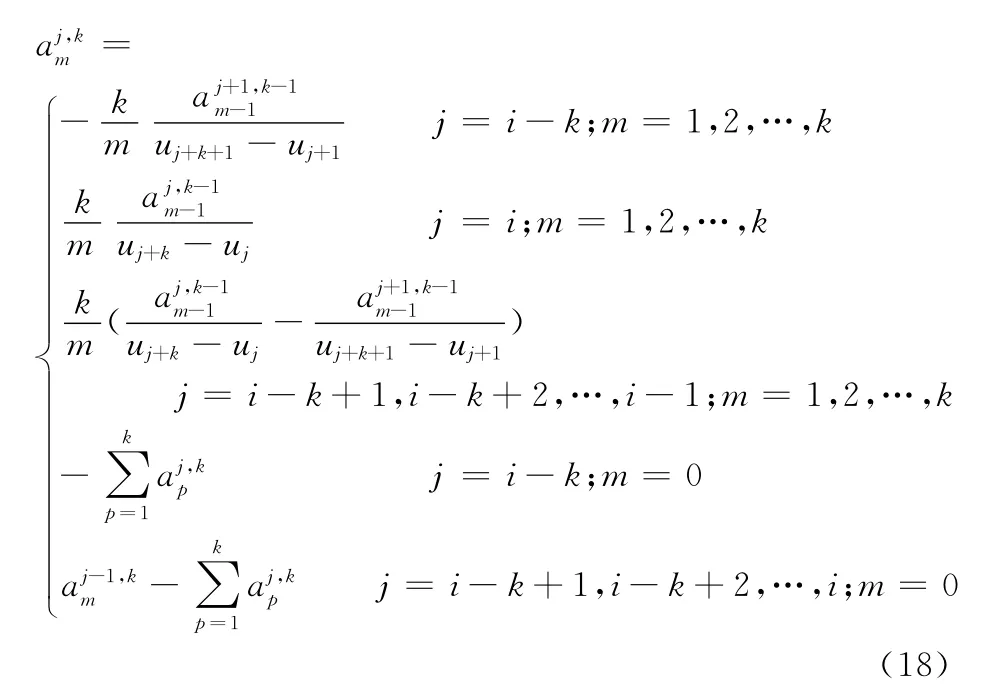
4.2 NURBS快速求導算法

由于NURBS曲線是有理分式形式，求導計算復雜，因此，可將式（1）寫成非有理形式：

即

對式（20）兩端求r階導數得

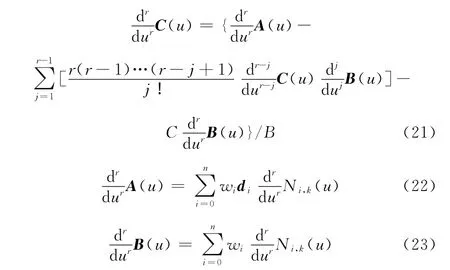
根據文獻［6］，Ni，k（u）的r階導數可由基函數Ni，k-r，Ni＋1，k-r，…，Ni＋r，k-r來計算，即

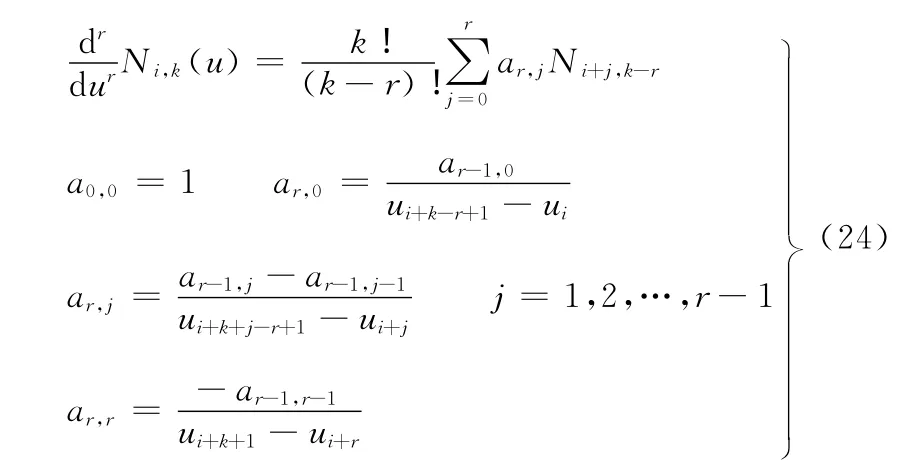
而基函 數 Ni，k-r，Ni＋1，k-r，…，Ni＋r，k-r已 經 在 上 節求值過程中得出，因此可直接調用。可見求導過程不需要遞推，只需進行四則運算即可，大大提高了運算效率。

4.3 快速算法效率分析

由以上分析可看出，NURBS的求值求導運算就是對非均勻B樣條基函數的運算，因此，本文針對計算NURBS曲線中的非均勻B樣條基函數所需計算次數來衡量算法時間復雜度，見表1。

表1 算法復雜度

Tmul、Tadd、Ttotal分別為乘除運算、加減運算、總運算次數。由表1可看出本文方法運算速度比傳統的de Boor-Cox方法快一倍多，具有更高的運算效率。

5 插補誤差處理

NURBS插補過程中存在兩種誤差，一種是軌跡誤差，一種是弓高誤差，如圖5所示，εi為軌跡誤差，δi為弓高誤差。為了達到較高的加工精度，插補過程中必須控制插補誤差。由以上分析可知，NURBS插補的每一插補點都在NURBS曲線上，因此不存在軌跡誤差，插補過程中誤差主要由弓高誤差引起，必須對弓高誤差進行控制。弓高誤差的計算是NURBS插補算法的主要任務之一，直接計算弓高誤差，計算復雜，計算量大，且影響插補的實時性，因此可采用近似算法。計算過程如下：以插補點C（ui）處的曲率半徑為半徑，以插補步長ΔLi為弦長，作圓弧ΔS′i，代替插補曲線弧ΔSi，如圖6所示，ρi為曲率半徑，δi為弓高誤差，可求得弓高誤差為

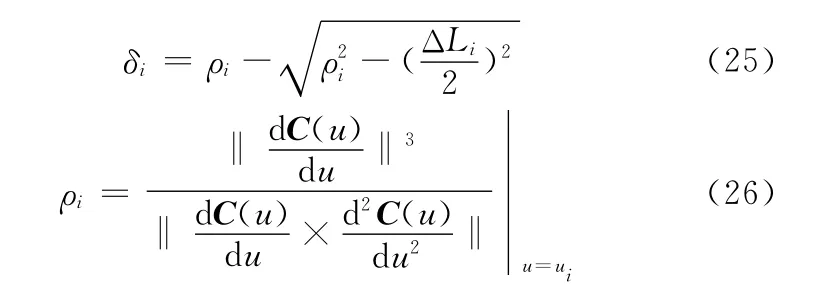
圖5 NURBS插補過程中的誤差

圖6 NURBS插補弓高誤差近似描述

由式（5）和式（25）可以看出，弓高誤差受進給速度和曲率半徑影響，進給速度越大，弓高誤差越大；反之，弓高誤差越小。在實際加工過程中，總是希望進給速度盡可能保持恒定，以獲得盡可能高的表面加工質量，但是，隨著曲線曲率的變化，弓高誤差可能會超出限定值，為了解決這個問題，本文采用自適應方法規劃進給速度，即當誤差未超過限定值時，以恒定的進給速度進行插補；當誤差超過限定值時，根據插補點的曲率半徑自適應調節進給速度。假定弓高誤差限定值為δmax，進給速度按下式進行自適應調節［3］：

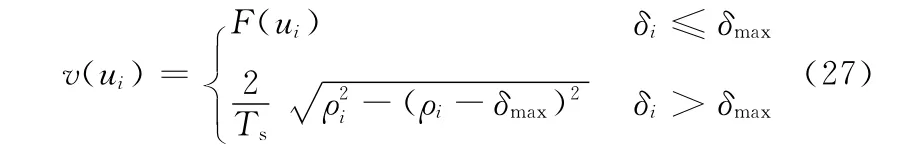
式中，F（ui）為ui處給定的進給速度。

6 仿真分析

為了驗證本文方法的可行性和有效性，采用MATLAB進行仿真驗證。分別對本文方法、一階泰勒展開法、二階泰勒展開法的速度波動率進行仿真，速度波動率按下式計算：

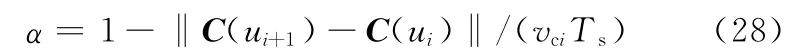
式中，vci為給定的進給速度。

仿真計算機 CPU 頻率為2.2GHz，內存2GB。NURBS曲線參數如表2所示，仿真曲線圖形如圖7所示。

表2 NURBS曲線參數表

圖7 NURBS曲線圖

本文方法、一階泰勒展開法、二階泰勒展開法的速度波動率仿真圖形分別如圖8～圖10所示。

圖8 本文方法速度波動率

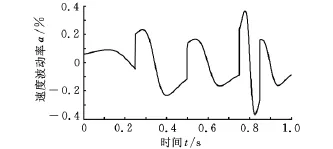
圖9 一階泰勒展開法速度波動率

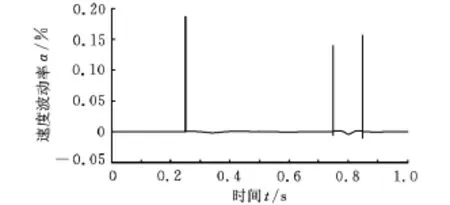
圖10 二階泰勒展開法速度波動率

由圖8～圖10可得出三種方法的平均速度波動率（表3），可以看出，本文方法的平均速度波動率最小。

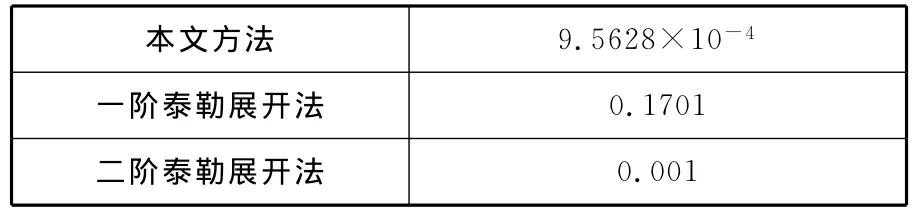
表3 平均速度波動率 %

7 結論

（1）本文方法能夠有效地減小速度波動，并保持進給速度的連續性，提高加工效率和表面質量。

（2）推導出NURBS快速求值、求導算法，提高了計算速度和插補實時性。

（3）插補速度隨弓高誤差限制自適應調節，提高了插補精度。

（4）仿真實例表明，本文方法可行、有效，為高性能NURBS插補器的開發提供了理論基礎。

［1］Emami M M，Arezoo B.A Look-ahead Command Generator with Control Over Trajectory and Chord Error for NURBS Curve with Unknown Arc Length［J］.Computer-aided Design，2010，42：625-632.

［2］Wang Junbin，Yau Hong-Tzong.Real-time NURBS Interpolator：Application to Short Linear Segments［J］.Int.J.Adv.Manuf.Technol.，2009，41（11／12）：1169-1185.

［3］Yeh S S，Hsu P L.Adaptive-feedrate Interpolation for Parametric Curves with a Confined Chord Error［J］.Computer-aided Design，2002，34（3）：229-237.

［4］趙國勇，徐志祥，趙福令.高速高精度數控加工中NURBS曲線插補的研究［J］.中國機械工程，2006，17（3）：291-294.Zhao Guoyong，Xu Zhixiang，Zhao Fuling.Study on NURBS Curve Interpolator in the High Speed and High Accuracy CNC Machining［J］.China Mechanical Engineering，2006，17（3）：291-294.

［5］Tsai M C，Cheng C W.A Real-Time Predictor-Corrector Interpolator for CNC Machining［J］.Journal of Manufacturing Science and Engineering，2003，125（3）：449-460.

［6］Piegl L，Tiller W.The NURBS Book［M］.2nd ed.Berlin：Springer，1997.

［7］Yan Cunliang，Du Daoshan，Li Congxin.Design of a Real-time Adaptive Interpolator with Parameter Compensation［J］.Int.J.Adv.Manuf.Technol.，2007，35（1／2）：169-178.

［8］金建新.機床CNC系統中任意空間曲線的可控步長插補方法［J］.機械工程學報，2000，36（4）：95-97.Jin jianxin.Prearranged Step Interpolation Method for Random-space-curve in CNC Machine Tool System［J］.Chinese Journal of Mechanical Engineering，2000，36（4）：95-97.

［9］Shen Hongyao，Fu Jianzhong，Fan Yongqiang.A New Adaptive Interpolation Scheme of NURBS Based on Axis Dynamics［J］.Int.J.Adv.Manuf.Technol.，2011，56（1／4）：215-221.

［10］王田苗，曹宇男，陳友東，等.基于de Boor算法的NURBS曲線插補和自適應速度控制研究［J］.中國機械工程，2007，18（21）：2608-2613.Wang Tianmiao，Cao Yunan，Chen Youdong，et al.NURBS Interpolation and Feedrate Adaptive Control Based on de Boor Algorithm［J］.China Mechanical Engineering，2007，18（21）：2608-2613.

［11］de Boor Carl.A Practical Guide to Splines［M］.New York：Springer-Verlag，2001.