基于等維新息灰色馬爾可夫模型的河流水質(zhì)預(yù)測

顏廷文，孫寶盛，張 冉

（天津大學(xué) 環(huán)境科學(xué)與工程學(xué)院，天津300072）

隨著我國經(jīng)濟(jì)的飛速發(fā)展，河流水污染這一全國性的問題受到越來越多的關(guān)注。河流水質(zhì)預(yù)測是維護(hù)、評價和管理當(dāng)前水質(zhì)狀況的重要依據(jù)，通過預(yù)測可以了解當(dāng)?shù)厮w環(huán)境質(zhì)量的演變趨勢，從而及時發(fā)現(xiàn)水質(zhì)惡化的原因并制定相應(yīng)的治理措施［1－2］。

自20世紀(jì)80年代以來，河流水質(zhì)預(yù)測模型的研究已經(jīng)有了很大進(jìn)展。根據(jù)模型原理的不同，目前比較典型的預(yù)測方法主要有數(shù)理統(tǒng)計預(yù)測法、灰色預(yù)測模型法、神經(jīng)網(wǎng)絡(luò)模型法和水質(zhì)模擬預(yù)測法等幾大類［3］。

由于影響水質(zhì)的因素具有復(fù)雜性，部分是確定已知的，部分是不確定未知的［4］，因此，水質(zhì)預(yù)測可采用灰色預(yù)測模型。它所需的信息少、對變化趨勢要求不高、運(yùn)算及檢驗方便，已在預(yù)測領(lǐng)域得到了廣泛應(yīng)用［5－7］。但傳統(tǒng)的灰色模型在建模過程中會受到數(shù)據(jù)隨機(jī)性擾動的影響，預(yù)測精度往往較差，需要對其進(jìn)行改進(jìn)。因此，本文構(gòu)建了一種等維新息灰色馬爾可夫預(yù)測模型，該模型先利用等維新息來改進(jìn)傳統(tǒng)灰色預(yù)測模型，再采用適合隨機(jī)變化動態(tài)系統(tǒng)的馬爾可夫鏈理論來改進(jìn)預(yù)測結(jié)果［6，8］。

1 等維新息灰色馬爾可夫模型

1.1 傳統(tǒng)灰色 GM（1，1）模型［9］

將原始數(shù)據(jù)序列x（0）＝｛x（0）（1），x（0）（2），…，x（0）（n）｝，進(jìn)行一次累加生成1－AGO，使得：

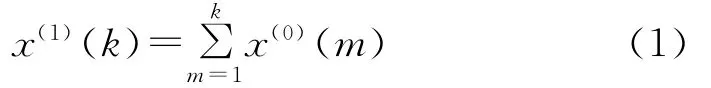
式中：x（0）——原始序列；x（1）——新序列；k＝1，2，…，n，m＝1，2，…，k。

即得到新的數(shù)據(jù)序列x（1）＝｛x（1）（1），x（1）（2），…，x（1）（n）｝。x（1）可以建立以下白化形式的 微 分方程：

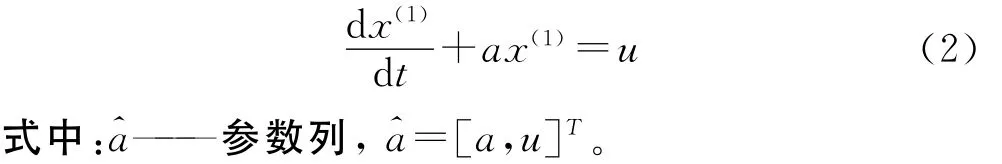
按最小二乘法解：

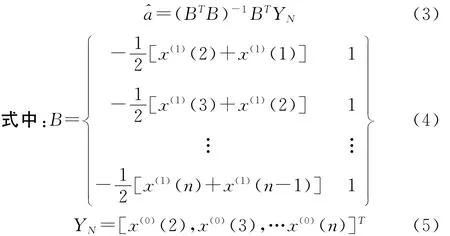
白化形式微分方程的解為：

將模型還原為：

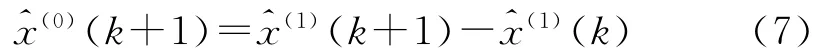
1.2 等維新息灰色預(yù)測模型

等維新息灰色預(yù)測模型是在傳統(tǒng)灰色GM（1，1）的基礎(chǔ)之上改進(jìn)而來的。將傳統(tǒng)灰色模型預(yù)測出的新數(shù)據(jù)加入到原始序列中，同時去掉最老的一個數(shù)據(jù)，保持?jǐn)?shù)列等維，再次建立灰色GM（1，1）模型，依次反復(fù)，直到完成預(yù)測目標(biāo)。這樣就可以把精度相對較高的數(shù)據(jù)和新出現(xiàn)的擾動因素及時考慮到模型中，突出最新的變化趨勢［10］。

在模型建立后，要對預(yù)測值進(jìn)行精度檢驗才能判定其合理性和有效性。對于等維新息灰色模型而言，主要檢驗以下4個方面：平均相對誤差（α）、絕對關(guān)聯(lián)度（ε）、均方差比（C）、小誤差概率（p）。

1.3 馬爾可夫模型

1.3.1 狀態(tài)劃分 對等維新息預(yù)測模型得到的結(jié)果進(jìn)行馬爾可夫修正，首先要作狀態(tài)劃分，即以一個具有馬氏鏈特點(diǎn)的非平穩(wěn)隨機(jī)序列曲線＾x（0）（t）為基準(zhǔn)，劃分出與之平行的若干曲線，每相鄰2條曲線之間的區(qū)域構(gòu)成一種狀態(tài)［11］，記為：

1.3.2 狀態(tài)轉(zhuǎn)移概率矩陣［11］設(shè)數(shù)據(jù)序列由狀態(tài)?i經(jīng)過n步轉(zhuǎn)移到?j的次數(shù)記為nij（n），狀態(tài)?i出現(xiàn)的次數(shù)記為ni，則由?i經(jīng)過n步轉(zhuǎn)移到?j的轉(zhuǎn)移概率為：

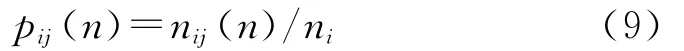
狀態(tài)轉(zhuǎn)移概率矩陣為：

1.3.3 馬爾科夫預(yù)測值 由上一步的初始狀態(tài)?i及狀態(tài)轉(zhuǎn)移概率矩陣P（n），可確定下一步等維新息灰色模型預(yù)測結(jié)果處于的狀態(tài)和相應(yīng)的概率。馬爾可夫預(yù)測值即各狀態(tài)預(yù)測區(qū)間的中值與其對應(yīng)的概率之乘積。

2 太湖流域水質(zhì)預(yù)測

2.1 數(shù)據(jù)來源

本文采用的數(shù)據(jù)為國家環(huán)境保護(hù)部數(shù)據(jù)中心公開的數(shù)據(jù)，選取太湖流域的上海青浦急水港點(diǎn)位的2004—2011年水質(zhì)指標(biāo)COD，NH3—N進(jìn)行建模預(yù)測。

2.2 傳統(tǒng)灰色GM（1，1）模型預(yù)測

以上海市青浦急水港2004—2011年的COD，NH3—N指標(biāo)作為原始數(shù)據(jù)序列，依次代入式（1）—（7），得到COD和NH3—N指標(biāo)的預(yù)測模型分別為式（11）和式（12）：

根據(jù)模型精度檢驗可得，傳統(tǒng)灰色GM（1，1）模型對于COD指標(biāo)的平均相對誤差為α＝3.03%，灰色絕對關(guān)聯(lián)度為ε＝0.997 3，均方差比為C＝0.172 5，小誤差概率為p＝0.875；傳統(tǒng)灰色 GM（1，1）模型對于NH3—N指標(biāo)的平均相對誤差為α＝6.49%，灰色絕對關(guān)聯(lián)度為ε＝0.995 4，均方差比為C＝0.314 4，小誤差概率為p＝1.0。

2.3 等維新息灰色模型預(yù)測

采用一次等維新息模型進(jìn)行傳統(tǒng)灰色模型改進(jìn)預(yù)測，首先利用傳統(tǒng)GM（1，1）模型預(yù)測2012年2項水質(zhì)指標(biāo)的數(shù)值，然后加入到已知原始數(shù)據(jù)列的最后位置，同時去掉最早的2004年的數(shù)據(jù)，最終以2005—2012年的數(shù)據(jù)作為輸入序列，建立新的灰色GM（1，1）模型，得到COD和NH3—N指標(biāo)的等維新息灰色預(yù)測模型，分別為式（13）和式（14），預(yù)測結(jié)果如表1所示：

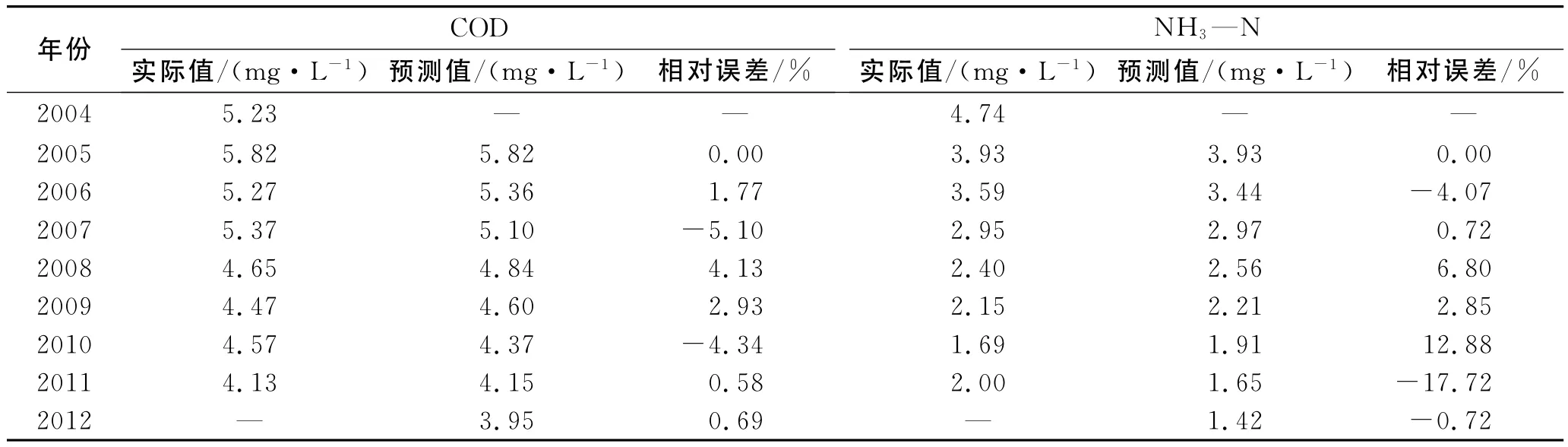
表1 等維新息灰色模型預(yù)測河流水質(zhì)

根據(jù)模型精度檢驗可得，等維新息灰色模型對于COD指標(biāo)的平均相對誤差為α＝2.79%，灰色絕對關(guān)聯(lián)度為ε＝0.998 8，均方差比為C＝0.151 7，小誤差概率為p＝1.0；等維新息灰色模型對于NH3—N指標(biāo)的平均相對誤差為α＝6.53%，灰色絕對關(guān)聯(lián)度為ε＝0.998 0，均方差比為C＝0.140 7，小誤差概率為p＝1.0。由以上數(shù)據(jù)顯示，對于COD指標(biāo)，利用等維新息灰色模型的預(yù)測結(jié)果在平均相對誤差、灰色絕對關(guān)聯(lián)度、均方差比、小誤差概率4個方面都好于傳統(tǒng)灰色預(yù)測模型，但對于NH3—N指標(biāo)，平均相對誤差沒有達(dá)到要求，因此，需要對NH3—N指標(biāo)的預(yù)測結(jié)果進(jìn)行馬爾可夫修正。

2.4 等維新息預(yù)測結(jié)果的馬爾可夫修正

2.4.1 狀態(tài)的劃分 在參考文獻(xiàn)［11-12］的基礎(chǔ)上，根據(jù)上述等維新息預(yù)測結(jié)果的平均相對誤差的實際情況，將預(yù)測結(jié)果劃分為5個狀態(tài)。

（1）極度高估狀態(tài)。相對誤差在［－20%，－15%］之間，2011年屬于此狀態(tài)。

（2）高估狀態(tài)。相對誤差在［－15%，－5%］之間，沒有屬于此狀態(tài)的年份。

（3）較為準(zhǔn)確狀態(tài)。相對誤差在［－5%，5%］之間，2006，2007，2009和2012年屬于此狀態(tài)。

（4）低估狀態(tài)。相對誤差在［5%，15%］之間，2008和2010年屬于此狀態(tài)。

（5）極度低估狀態(tài)。相對誤差在［15%，20%］之間，沒有屬于此狀態(tài)的年份。

2.4.2 狀態(tài)轉(zhuǎn)移矩陣 由各年份所處的狀態(tài)及其狀態(tài)轉(zhuǎn)移情況，可求得1步轉(zhuǎn)移矩陣為：

2.4.3 馬爾可夫預(yù)測結(jié)果 由以上的1步轉(zhuǎn)移矩陣，可以計算出n步轉(zhuǎn)移矩陣，并預(yù)測出未來5a NH3—N指標(biāo)處于各狀態(tài)的概率值，進(jìn)而計算相應(yīng)的馬爾可夫預(yù)測值，其結(jié)果如表2所示。

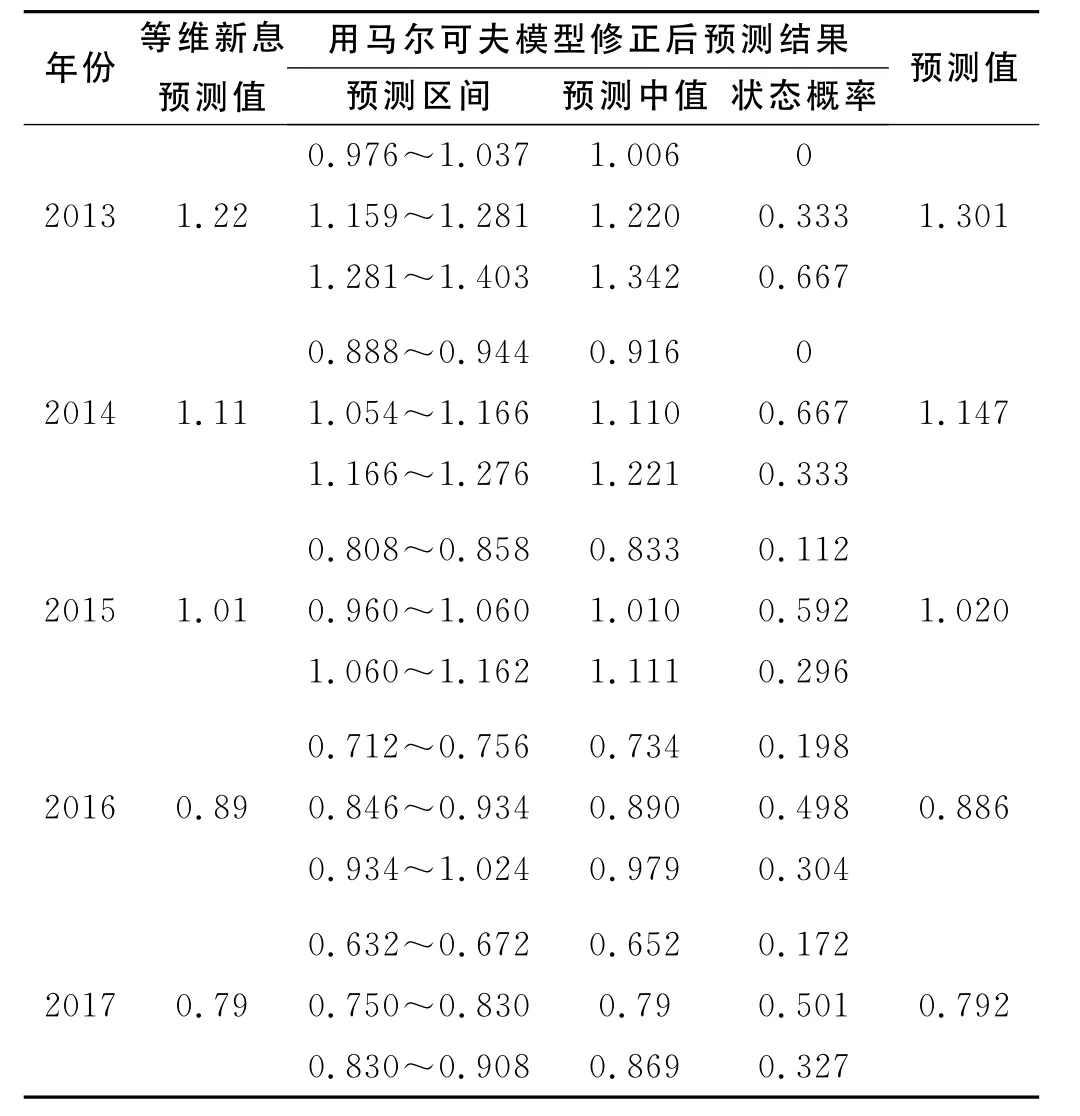
表2 NH3－N指標(biāo)的等維新息灰色預(yù)測值的馬爾可夫修正結(jié)果

表2的預(yù)測結(jié)果顯示，對于2013—2017年的絕大多數(shù)年份來說，最大概率為較為準(zhǔn)確狀態(tài)；次大概率為低估狀態(tài)。由此可見，等維新息預(yù)測結(jié)果經(jīng)過馬爾可夫修正之后，將降低結(jié)果高估和極度低估的概率。

2.5 水質(zhì)指標(biāo)的預(yù)測結(jié)果

太湖流域上海市青浦區(qū)急水港點(diǎn)位水質(zhì)指標(biāo)COD的預(yù)測值與實際值的比較結(jié)果見圖1。水質(zhì)指標(biāo)NH3—N的預(yù)測值與實際值的比較結(jié)果見圖2。

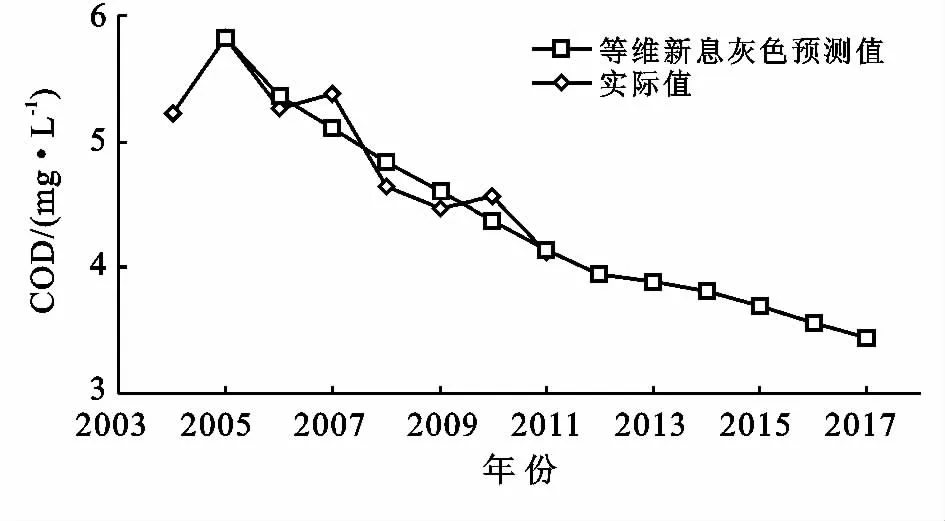
圖1 COD指標(biāo)實際值與等維新息灰色預(yù)測值

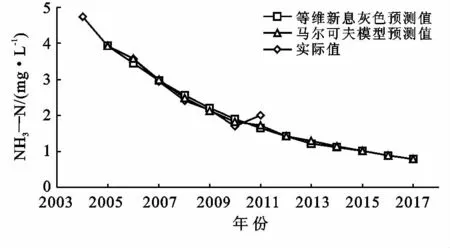
圖2 NH3－N指標(biāo)實際值與兩種預(yù)測值

由圖1可以看出，2004—2011年COD指標(biāo)實際值呈下降趨勢，等維新息預(yù)測結(jié)果的平均相對誤差、灰色絕對關(guān)聯(lián)度、均方差比、小誤差概率均達(dá)到精度要求，預(yù)測結(jié)果可信。根據(jù)等維新息的預(yù)測結(jié)果，COD指標(biāo)在未來幾年中大體呈現(xiàn)下降趨勢，并逐漸趨于平緩，在2017達(dá)到3.44mg／L。

由圖2可以看出，2004—2011年NH3—N指標(biāo)實際值呈整體下降趨勢，但有小幅度波動，對應(yīng)的等維新息預(yù)測模型的相對平均誤差為7.47%，馬爾可夫修正后，相對平均誤差為4.66%。因此可以說明，通過馬爾可夫模型修正過程可以有效地減小等維新息預(yù)測結(jié)果的相對誤差，使預(yù)測結(jié)果更為準(zhǔn)確。根據(jù)馬爾可夫模型修正后的預(yù)測結(jié)果，NH3—N指標(biāo)在未來幾年中將繼續(xù)呈現(xiàn)下降趨勢，并在一定程度上趨于平緩，在2017年達(dá)到0.792mg／L。

3 水質(zhì)分析及建議

太湖流域地處長江三角洲地區(qū)，河網(wǎng)密布，湖泊眾多。其中，太湖是我國第3大淡水湖泊，兼有供水、蓄洪、灌溉、航運(yùn)、旅游等功能。近年來，隨著沿湖城市的經(jīng)濟(jì)發(fā)展，排入太湖流域的污染物不斷增加，導(dǎo)致其水環(huán)境受到嚴(yán)重影響。對此，各級政府采取了一系列措施對流域進(jìn)行整治，如加大對點(diǎn)源和面源污染物控制，增大引江水量，對重點(diǎn)湖區(qū)進(jìn)行清淤及生態(tài)修復(fù)等［13］。從太湖流域歷年的水質(zhì)指標(biāo)數(shù)據(jù)及以上的預(yù)測結(jié)果可以顯示出，經(jīng)過這些年的努力，太湖流域水環(huán)境治理已經(jīng)取得初步成效，流域的COD及NH3—N指標(biāo)雖有小范圍波動，但總體看來呈逐漸下降趨勢。

由于太湖污染的長期積累，已經(jīng)形成的水質(zhì)條件很難在短期內(nèi)得到根本改變，加之現(xiàn)有的入湖污染仍遠(yuǎn)超湖體允許的納污能力，太湖流域的水環(huán)境形勢依然嚴(yán)峻。因此，我們應(yīng)該繼續(xù)推行有效的治理措施，并在現(xiàn)有的實踐經(jīng)驗上，探索更深入的治理及修復(fù)方法。

（1）減少湖體污染，增加其環(huán)境容量。要求沿湖企業(yè)達(dá)標(biāo)排放，削減污染物入湖量，這是解決污染問題的根本；限定水工程的建設(shè)和企業(yè)取排水范圍，引水濟(jì)湖，改變?nèi)牒此|(zhì)，加快水體交換及自凈，提高湖泊環(huán)境容量值。

（2）持續(xù)實施生態(tài)清淤，保持污染物入湖與出湖的平衡。將表層的污染污泥清除出去，切斷湖泛發(fā)生的生物鏈，并直接清除滯留在湖區(qū)的污染物，標(biāo)本兼治。

（3）加快轉(zhuǎn)變太湖流域經(jīng)濟(jì)發(fā)展方式。合理發(fā)展城市經(jīng)濟(jì)，合理利用和開發(fā)土地，令沿湖城市社會經(jīng)濟(jì)發(fā)展方式由粗放型向集約型轉(zhuǎn)變［14－15］，將太湖流域水資源、水環(huán)境和水生態(tài)保護(hù)擺在發(fā)展的優(yōu)先位置［16］。支持發(fā)展低碳經(jīng)濟(jì)、循環(huán)經(jīng)濟(jì)、綠色經(jīng)濟(jì)［14－15］。

（4）完善流域管理體制，積極推動流域綜合管理。加強(qiáng)流域立法，制定區(qū)域統(tǒng)籌的法律法規(guī)體系。打破區(qū)域的硬性分割，建立統(tǒng)一的流域綜合管理機(jī)構(gòu)，加深開發(fā)與保護(hù)并重的管理理念［16］。

4 結(jié)論

本文采用等維新息—灰色馬爾可夫模型對太湖流域上海青浦急水港點(diǎn)位的COD及NH3—N水質(zhì)指標(biāo)進(jìn)行預(yù)測，為河流水質(zhì)預(yù)測提供參考依據(jù)。

針對COD指標(biāo)，應(yīng)用等維新息模型對傳統(tǒng)灰色模型進(jìn)行改進(jìn)，加入最新數(shù)據(jù)，克服了傳統(tǒng)灰色模型固定不變的缺陷，提高了預(yù)測精度，結(jié)果顯示其在平均相對誤差、灰色絕對關(guān)聯(lián)度等方面都有顯著提高。

針對NH3—N指標(biāo)，由于其具有波動性，故將等維新息預(yù)測結(jié)果進(jìn)行馬爾可夫修正，目的是減小相對平均偏差，提高預(yù)測結(jié)果的準(zhǔn)確率。通過計算狀態(tài)轉(zhuǎn)移矩陣，得到未來年份中NH3—N指標(biāo)所處的濃度范圍，再通過計算得到更為精確的預(yù)測值。

通過對太湖流域水質(zhì)的預(yù)測，可以看到近幾年太湖流域水環(huán)境治理工作已初見成效，但未來的治理任務(wù)依舊任重道遠(yuǎn)，要想從根本上解決太湖流域水體污染問題，就要從大局著眼，控制源頭污染，進(jìn)行生態(tài)清淤，加快轉(zhuǎn)變沿湖城市經(jīng)濟(jì)發(fā)展方式，以期實現(xiàn)太湖流域水環(huán)境的整體改善。

［1］ 邱林，黃鑫，李洪良.基于模糊權(quán)馬爾可夫模型的綜合水質(zhì)預(yù)測［J］.人民長江，2007，38（1）：75-77.

［2］ Huang G H，Xia J.Barriers to sustainable water quality management［J］.Journal of Environmental Management，2001，61（1）：1-23.

［3］ 李娜，王臘春，謝剛，等.山東省轄淮河流域河流水質(zhì)趨勢的灰色預(yù)測［J］.環(huán)境科學(xué)與技術(shù)，2012，35（2）：195-199.

［4］ 蘇彩紅，向娜，陳廣義，等.基于人工蜂群算法與BP神經(jīng)網(wǎng)絡(luò)的水質(zhì)評價模型［J］.環(huán)境工程學(xué)報，2012，6（2）：699-704.

［5］ 王丙參，夏鴻鳴，魏艷華.基于 GM（1，1）模型的渭河水質(zhì)預(yù)測［J］.牡丹江大學(xué)學(xué)報，2012，21（3）：123-124.

［6］ 李明然，田林亞，洪毅.改進(jìn)的灰色馬爾科夫模型在大壩變形預(yù)測中的應(yīng)用［J］.水利與建筑工程學(xué)報，2012，10（3）：65-66.

［7］ Deng J L.Introduction to grey system theory［J］.Journal of Grey System，1989，1（1）：1-24.

［8］ 趙曉梅，蓋美.基于等維新息灰色馬爾可夫模型的大連城市用水量預(yù)測［J］.水文，2011，31（1）：66-69.

［9］ 鄧聚龍.灰色系統(tǒng)基本方法［M］.武漢：華中理工大學(xué)出版社，1996：104-105.

［10］ 胡惠方，吳澤寧.等維新息 GM（1，1）模型在鄭州市城市生活需水量預(yù)測中的應(yīng)用［J］.氣象與環(huán)境科學(xué)，2007，30（1）：17-20.

［11］ 高蔚.基于 Markov理論的改進(jìn)灰色GM（1，1）預(yù)測模型研究［J］.計算機(jī)工程與科學(xué)，2011，33（2）：159-163.

［12］ 卞煥清，夏樂天.基于灰色馬爾可夫鏈模型的人口預(yù)測［J］.數(shù)學(xué)的實踐與認(rèn)識，2012，42（7）：127-132.

［13］ 陳潤，錢磊，申金玉，等.2007年水危機(jī)后太湖水質(zhì)評價［J］.水電能源科學(xué)，2012，30（2）：32-34.

［14］ 呂振霖.太湖水環(huán)境綜合治理的實踐與思考［J］.河海大學(xué)學(xué)報：自然科學(xué)版，2012，40（2）：123-128.

［15］ 蒲勇平.長江流域生態(tài)修復(fù)工程的意義及對策［J］.水土保持通報，2002，22（5）：9-11.

［16］ 楊桂山.長江水問題基本態(tài)勢及其形成原因與防控策略［J］.長江流域資源與環(huán)境，2012，21（7）：821-830.