一種改進(jìn)魯棒KPCA 算法及其在齒輪泵故障診斷中的應(yīng)用

王濤，李艾華，王旭平，蔡艷平，姚良

(第二炮兵工程大學(xué)機(jī)電工程系，陜西西安710025)

主元分析 (Principal Component Analysis，PCA)方法是一種常用的特征提取方法，但PCA 方法只能解決線性問(wèn)題，并不適合分析非線性問(wèn)題。為了提高PCA 方法的適用性，B SCH?LKOPF 等提出了核主元分析(Kernel PCA，KPCA)方法［1］。由于KPCA 在解決非線性問(wèn)題方面展現(xiàn)出的優(yōu)勢(shì)，使其在人臉識(shí)別、高光譜圖像降維、過(guò)程監(jiān)控、機(jī)械故障診斷等領(lǐng)域得到了成功應(yīng)用［2－5］。雖然，KPCA 是最優(yōu)秀的非線性PCA 算法之一，但由于它是基于最小化方均根誤差準(zhǔn)則實(shí)現(xiàn)的，因此和傳統(tǒng)PCA 方法一樣，當(dāng)輸入樣本中存在野點(diǎn)(或噪聲)時(shí)，KPCA 算法一樣會(huì)變得很不穩(wěn)定。為了增強(qiáng)經(jīng)典KPCA 算法的魯棒性，已經(jīng)有學(xué)者提出了一些改進(jìn)算法。文獻(xiàn)［6］ 提出在特征空間計(jì)算映射樣本φ(x)的重構(gòu)誤差，當(dāng)誤差大于某一給定閾值ε 時(shí)，將其識(shí)別為野點(diǎn)并加以剔除，從而消除噪聲對(duì)KPCA 的影響;文獻(xiàn)［7］ 基于加權(quán)協(xié)方差的特征值分解提出一種魯棒KPCA 算法，通過(guò)給異常樣本賦予較小權(quán)值來(lái)抵抗數(shù)據(jù)污染和模型偏差，從而增強(qiáng)經(jīng)典KPCA 的魯棒性。針對(duì)大訓(xùn)練集問(wèn)題，文獻(xiàn)［8 －9］ 提出了迭代式魯棒KPCA 算法，有效降低了計(jì)算負(fù)擔(dān)和內(nèi)存開(kāi)銷。相對(duì)于樣本數(shù)目動(dòng)輒成千上萬(wàn)、特征維數(shù)好幾百的語(yǔ)音識(shí)別和圖像識(shí)別等問(wèn)題而言，不論機(jī)械設(shè)備故障還是液壓系統(tǒng)故障，其故障樣本數(shù)量不但相對(duì)較少，而且樣本維數(shù)也較小。因此作者僅探討如何增強(qiáng)KPCA 的魯棒性，并不涉及KPCA 算法的迭代計(jì)算問(wèn)題。文獻(xiàn)［6］ 所提算法是最早見(jiàn)諸文獻(xiàn)的魯棒KPCA 算法之一，它建立了特征空間中識(shí)別野點(diǎn)的準(zhǔn)則，并在仿真數(shù)據(jù)上驗(yàn)證了該算法對(duì)消除野點(diǎn)影響具有較好的效果。但該算法存在重構(gòu)誤差表達(dá)式不便于使用、給定閾值難以確定和計(jì)算步驟過(guò)于復(fù)雜等問(wèn)題。為了提高該算法的實(shí)用性，作者針對(duì)上述問(wèn)題進(jìn)行改進(jìn)，并將其應(yīng)用于齒輪泵故障診斷中。

1 改進(jìn)魯棒KPCA 算法

1.1 信號(hào)重構(gòu)最小誤差準(zhǔn)則

按照文獻(xiàn)［6］ 所述，信號(hào)重構(gòu)最小誤差準(zhǔn)則的基本原理是:設(shè)y = WTx 作為從輸入n 維隨機(jī)向量x 獲取的主分量，u=Wy 是輸入向量x 的重構(gòu)信號(hào)，則e=x－u 是重構(gòu)誤差。定義誤差函數(shù)J(W)如下:

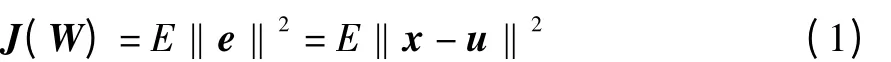
對(duì)于訓(xùn)練樣本集，誤差函數(shù)的估計(jì)為:

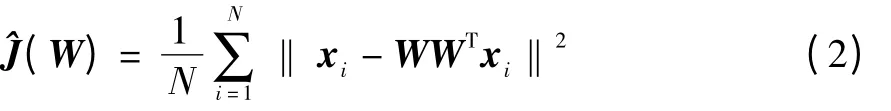
其中:W 的列向量是單位向量，且它們之間線性不相關(guān)，因此誤差函數(shù)的優(yōu)化目標(biāo)就是最大限度地減小由于降維而造成的信號(hào)損失。在輸入空間中，設(shè)W由輸入隨機(jī)向量x 的前m 個(gè)主元構(gòu)成，且ε ＞0 是一個(gè)給定的閾值，則將輸入變量xi識(shí)別為野點(diǎn)的準(zhǔn)則為:

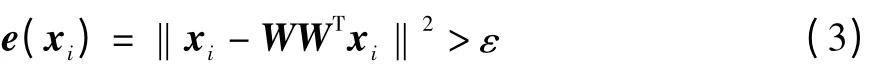
KPCA 通過(guò)非線性映射函數(shù)φ 將原始輸入數(shù)據(jù)X變換到一個(gè)高維特征空間F，原始數(shù)據(jù)xi在特征空間F 中的像為φ (xi)。將式(3)表示的準(zhǔn)則推廣到特征空間，則特征空間中的信號(hào)重構(gòu)誤差可表示為:

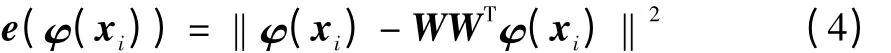
借助核方法的思想，用核函數(shù)K(xi，xj)=φ(xi)·φ(xj)改寫(xiě)式(4)，得到如下表達(dá)式:

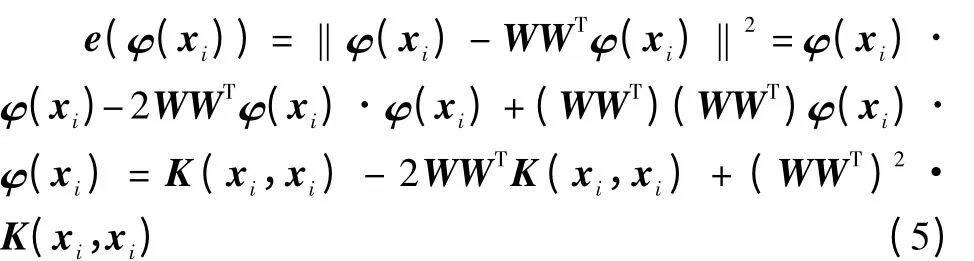
通過(guò)式(5)就可以計(jì)算得到特征空間中信號(hào)的重構(gòu)誤差。

1.2 改進(jìn)魯棒KPCA 算法描述

文獻(xiàn)［6］基于信號(hào)重構(gòu)最小誤差準(zhǔn)則提出了一種魯棒KPCA 算法，其基本思想是:首先根據(jù)算法給出的準(zhǔn)則對(duì)W 進(jìn)行估計(jì);然后利用W 的估計(jì)識(shí)別和消除野點(diǎn)，得到更精確W 的估計(jì)，重復(fù)上述過(guò)程直至計(jì)算得到相對(duì)精確的W;最后計(jì)算整個(gè)訓(xùn)練集的重構(gòu)誤差，并將具有相對(duì)較大重構(gòu)誤差的樣本設(shè)置為野點(diǎn)。該算法不僅保留了KPCA 的非線性屬性，而且魯棒性更好，有效增強(qiáng)了KPCA 的精度。但在實(shí)際應(yīng)用中，該算法還存在以下3 個(gè)問(wèn)題:

(1)根據(jù)式 (5)的表達(dá)形式，計(jì)算得到的e(φ(xi))是一個(gè)矢量矩陣，而不是一個(gè)標(biāo)量數(shù)值，不便于野點(diǎn)識(shí)別;

(2)利用一個(gè)給定閾值ε 識(shí)別野點(diǎn)在理論上可行，但在實(shí)際應(yīng)用中確定ε 非常困難;

(3)在特征空間中對(duì)樣本集進(jìn)行聚類，雖有助于提高精度，但增加了算法的復(fù)雜性和計(jì)算代價(jià)。

針對(duì)上述問(wèn)題，作者對(duì)該算法進(jìn)行了以下改進(jìn):

(1)將式(5)修改為

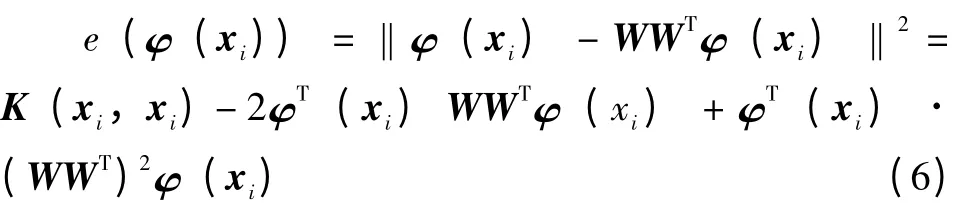
這樣計(jì)算得到的e(φ(xi))為一個(gè)標(biāo)量數(shù)值，便于野點(diǎn)識(shí)別;

(2)通過(guò)預(yù)先定義訓(xùn)練樣本集中的野點(diǎn)數(shù)目來(lái)確定算法的迭代和終止條件，而非給定閾值ε;

(3)直接對(duì)樣本集進(jìn)行KPCA 分析，取消在特征空間中聚類樣本集的環(huán)節(jié)，簡(jiǎn)化算法計(jì)算步驟。

綜上所述，對(duì)于一個(gè)給定的訓(xùn)練集X = {x1，x2，…，xM}，改進(jìn)魯棒KPCA 算法的步驟如下:

步驟1，初始化迭代步數(shù)k=0，將待處理的樣本集設(shè)為Y=X，即野點(diǎn)樣本的數(shù)目O(k)= 0 ;

步驟2，采用KPCA 分析樣本集，得到估計(jì)矩陣W(k);

步驟3，在特征空間中歸一化估計(jì)矩陣W(k);

步驟4，根據(jù)W(k)，利用式(6)計(jì)算訓(xùn)練樣本的重構(gòu)誤差;

步驟5，設(shè)置迭代步數(shù)k =k +1，在最后一步中從樣本集X 中消除具有最大重構(gòu)誤差的樣本，并設(shè)野點(diǎn)樣本的數(shù)目為O(k +1)= O(k)+1 。用保留的樣本重組待處理的新樣本集Y;

步驟6，如果W(k+1)滿足收斂條件，則中止迭代計(jì)算，否則跳到步驟4。

2 齒輪泵故障診斷實(shí)例

以某液壓實(shí)驗(yàn)臺(tái)上的CB－KP63 型高壓齒輪泵為對(duì)象，研究改進(jìn)魯棒KPCA 算法對(duì)齒輪泵不同狀態(tài)的識(shí)別。實(shí)驗(yàn)中，設(shè)置了側(cè)板磨損、齒輪磨損、軸承磨損3 類故障。對(duì)于包括正常在內(nèi)的齒輪泵4 種常見(jiàn)工作狀態(tài)，分別測(cè)取了從空載直到出口壓力為20 MPa時(shí)的泵殼振動(dòng)加速度信號(hào)，壓力上升間隔為1 MPa，每種情況各測(cè)取了40 組數(shù)據(jù)。針對(duì)齒輪泵的4 種工作狀態(tài)(正常狀態(tài)、側(cè)板磨損、齒輪磨損、軸承磨損分別對(duì)應(yīng)狀態(tài)1、狀態(tài)2、狀態(tài)3、狀態(tài)4)，各取原始采樣數(shù)據(jù)20 組，共80 組數(shù)據(jù)構(gòu)成訓(xùn)練樣本集Λ。向樣本集Λ 中隨機(jī)插入3%的野點(diǎn)，形成新的訓(xùn)練樣本集Ξ。各取原始采樣數(shù)據(jù)40 組，共160 組數(shù)據(jù)構(gòu)成測(cè)試樣本集Π。

對(duì)上述3 個(gè)數(shù)據(jù)集Λ、Ξ和Π，首先用3 層小波包分解原始采樣數(shù)據(jù)，小波基為db5，每個(gè)采樣數(shù)據(jù)被分解為8 個(gè)頻帶，計(jì)算各頻帶能量特征并進(jìn)行歸一化處理，然后以8 個(gè)頻帶的歸一化能量構(gòu)造8 維特征向量。齒輪泵四種運(yùn)行狀態(tài)典型的歸一化頻帶能量特征如表1 所示。

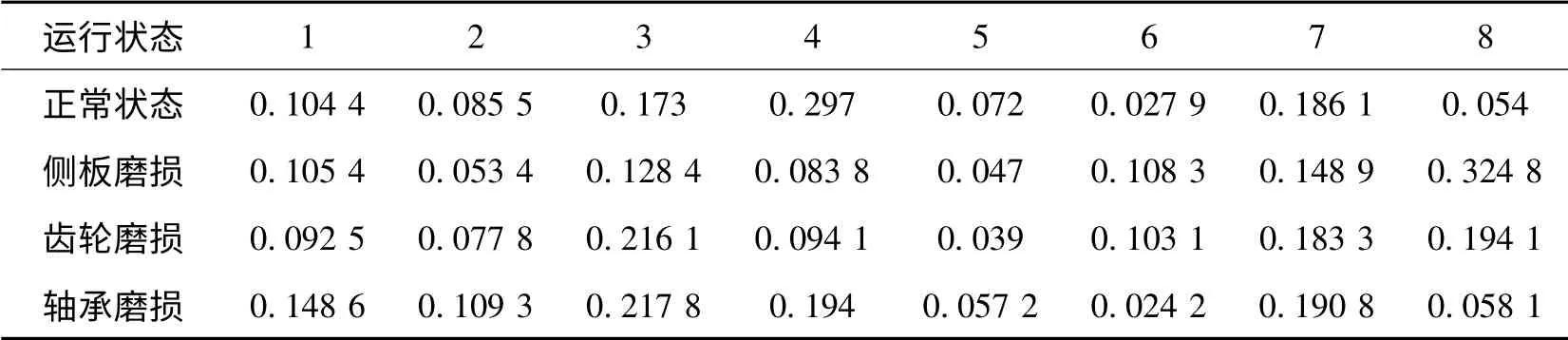
表1 齒輪泵4 種運(yùn)行狀態(tài)的特征組成

將小波包分解得到的特征向量集分別進(jìn)行KPCA和魯棒KPCA 分析，核函數(shù)選用徑向基核函數(shù)，核參數(shù)σ = 0.25 。

首先，應(yīng)用KPCA 對(duì)樣本集Λ 和樣本集Ξ 進(jìn)行分析，結(jié)果如圖1、2 所示。為了更直觀地觀察齒輪泵各種狀態(tài)特征樣本集的可分性，將其投影到二維平面顯示。按照特征值由大到小，從左至右、從上至下分別顯示第1 到第8 主元之間的投影圖。圖中，圓圈表示正常狀態(tài)樣本，加號(hào)表示側(cè)板磨損樣本，實(shí)心點(diǎn)表示齒輪磨損樣本，星號(hào)表示軸承磨損樣本。

圖1 是KPCA 對(duì)不帶野點(diǎn)樣本集Λ 的分析結(jié)果。可知:KPCA 在不帶野點(diǎn)的樣本集上具有較高的精度，第一個(gè)主元就基本實(shí)現(xiàn)了齒輪泵4 種狀態(tài)的分離，接下來(lái)的7 個(gè)主元更細(xì)致地實(shí)現(xiàn)了4 種狀態(tài)的區(qū)分。雖然軸承磨損樣本和正常狀態(tài)樣本有少許交疊，但仍能有效將這兩種狀態(tài)區(qū)分開(kāi)，從整體上看并未影響分類效果。

圖2 是KPCA 對(duì)帶野點(diǎn)樣本集Ξ的分析結(jié)果。可知:野點(diǎn)對(duì)KPCA 的主元產(chǎn)生了很大影響，加入的3%野點(diǎn)樣本導(dǎo)致各個(gè)主元無(wú)法區(qū)分開(kāi)齒輪泵的4 種狀態(tài)。除了側(cè)板磨損狀態(tài)能夠較好區(qū)分外，其他狀態(tài)特征樣本交疊嚴(yán)重，已不具備可分性。由此可見(jiàn)，對(duì)于帶野點(diǎn)的數(shù)據(jù)，KPCA 很不穩(wěn)定。

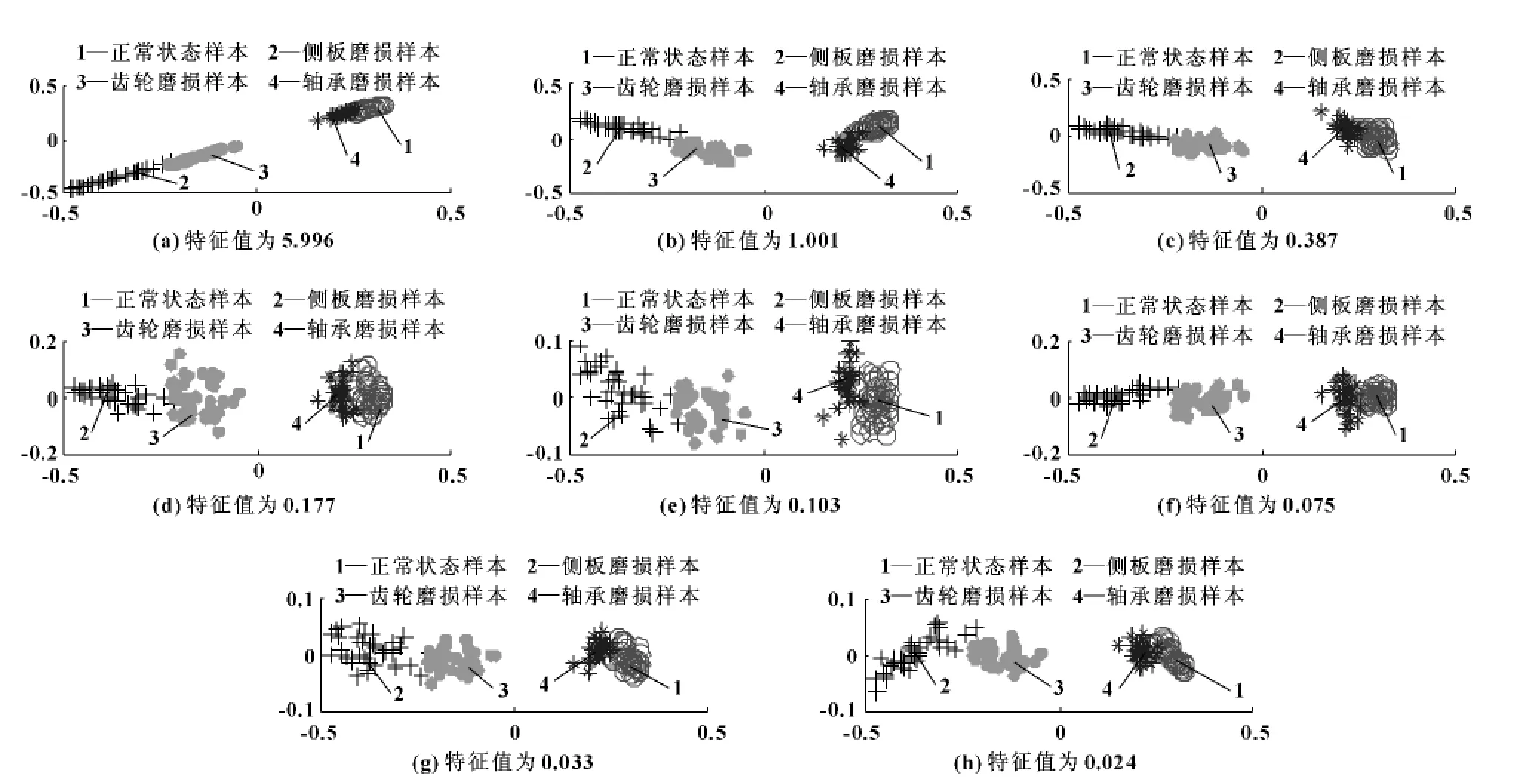
圖1 KPCA 算法對(duì)不帶野點(diǎn)樣本集的分析結(jié)果

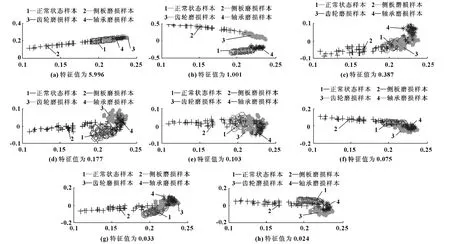
圖2 KPCA 算法對(duì)帶野點(diǎn)樣本集的分析結(jié)果

接著，應(yīng)用改進(jìn)魯棒KPCA 對(duì)樣本集Λ 和樣本集Ξ進(jìn)行分析，結(jié)果如圖3、4 所示。圖3 是改進(jìn)魯棒KPCA 對(duì)不帶野點(diǎn)樣本集Λ 的分析結(jié)果。可知:對(duì)于不帶野點(diǎn)的樣本集，改進(jìn)魯棒KPCA 算法也能夠獲得非常精確的主元，實(shí)現(xiàn)齒輪泵4 種狀態(tài)的有效區(qū)分。

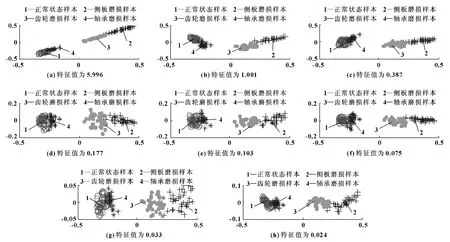
圖3 改進(jìn)魯棒KPCA 算法對(duì)不帶野點(diǎn)樣本集的分析結(jié)果

圖4 改進(jìn)魯棒KPCA 算法對(duì)帶野點(diǎn)樣本集的分析結(jié)果

對(duì)于帶野點(diǎn)的樣本集Ξ，采用改進(jìn)魯棒KPCA 算法進(jìn)行分析，結(jié)果如圖4 所示。可知:第一個(gè)主元就已經(jīng)消除了噪聲的影響。因此，改進(jìn)魯棒KPCA 算法能夠獲得近似精確的主元。在接下來(lái)的7 個(gè)主元上，噪聲的影響也很輕微，幾乎得到了和在不帶野點(diǎn)樣本集上一樣的分類效果。可見(jiàn)，改進(jìn)魯棒KPCA 算法相比KPCA 具有更好的抗噪性。

3 結(jié) 論

在簡(jiǎn)要介紹現(xiàn)有魯棒KPCA 算法的基礎(chǔ)上，針對(duì)故障診斷問(wèn)題樣本數(shù)量少且樣本維數(shù)低的特點(diǎn)，對(duì)文獻(xiàn)［6］所提算法進(jìn)行了改進(jìn)。改進(jìn)魯棒KPCA 算法在保持原算法抗噪性強(qiáng)優(yōu)點(diǎn)的同時(shí)，步驟更簡(jiǎn)單、更易編程實(shí)現(xiàn)，有效提高了算法的工程實(shí)用性。將改進(jìn)魯棒KPCA 算法應(yīng)用于齒輪泵故障特征提取中，與KPCA 算法相比，改進(jìn)魯棒KPCA 算法的抗噪性能明顯增強(qiáng)，能有效區(qū)分齒輪泵的不同故障模式。

【1】SCH?LKOPF B，SMOLA A，MüLLER K R.Nonlinear Component Analysis as a Kernel Eigenvalue Problem［J］.Neural Computation，1998，10(5):1299 －1319.

【2】WEN Ying，HE Lianghua，SHI Pengfei. Face Recognition Using Difference Vector Plus KPCA［J］.Digital Signal Processing，2012 (22):140 －146.

【3】王瀛，郭雷，梁楠.基于優(yōu)選樣本的KPCA 高光譜圖像降維方法［J］.光子學(xué)報(bào)，2011，40(6):847 －851.

【4】?VOKELJ Matej，ZUPAN Samo，PREBIL Ivan. Non－linear Multivariate and Multiscale Monitoring and Signal Denoising Strategy Using Kernel Principal Component Analysis Combined with Ensemble Empirical Mode Decomposition Method［J］. Mechanical Systems and Signal Processing，2011(25):2631 －2653.

【5】蔣靜，李志農(nóng)，易小兵.基于Volterra 級(jí)數(shù)和KPCA 的旋轉(zhuǎn)機(jī)械故障診斷方法研究［J］. 噪聲與振動(dòng)控制，2010(2):119 －122.

【6】LU Congde，ZHANG Taiyi，ZHANG Ruonan，et al.Adaptive Robust Kernel PCA Algorithm［C］// ICASSP，2003:621 －624.

【7】HUANG Su－Yun，YEH Yi－Ren，EGUCHI Shinto. Robust Kernel Principal Component Analysis［J］. Neural Computation，2009，21(11):3179 －3213.

【8】WANG Lei，PANG Yan－Wei，SHEN Dao－Yi，et al.An Iterative Algorithm for Robust Kernel Principal Component Analysis［C］//Proceedings of the Sixth International Conference on Machine Learning and Cybernetics，Hongkong，2007:3484 －3489.

【9】HUANG Hsin－Hsiung，YEH Yi－Ren.An Iterative Algorithm for Robust Kernel Principal Component Analysis［J］. Neurocomputing，2011(74):3921 －3930.