產生有毒物質的浮游植物—浮游動物離散動力學模型分析

顧恩國,張梅娜,陳 博

(中南民族大學 數學與統計學學院,武漢 430074)

一直以來,關于漁業資源的可持續發展的研究有很多,許多學者也建立了大量的模型[1-3],但是近年來,隨著對海洋資源可持續利用研究的深入,越來越多的學者注意到位于海洋食物鏈較低層的浮游生物,對海洋資源的可持續發展有著至關重要的影響,并且由此建立了一系列的數學模型[4-6].在已經建立的模型中,浮游植物、浮游動物相互作用的動態模型大多是在微分方程或者連續動力學基礎上提出的,用離散動力學模型進行研究的學者很少,而對于人類的捕撈對浮游生物的影響的研究更是稀少,另一方面,由于部分浮游植物會產生有毒物質,過度累積也會造成浮游動物的死亡.因此,本文將有毒的浮游植物、浮游動物被捕撈的連續模型離散化,建立一個在相同捕撈力度下,浮游植物、浮游動物的變化規律的離散動力學模型,用來研究人類的捕撈力度對整個浮游生物演化的影響,進而討論對海洋資源可持續利用的影響.

1 模型的建立

Lü Yunfei 和Pei Yongzhen等[5]提出的有毒浮游植物——浮游動物捕撈的連續動力學模型:

(1)

這里,P為在時刻t可產生有毒物質的浮游植物的種群密度,Z為在時刻t浮游動物的種群密度,并且滿足在初始時刻P(0)=P0≥0,Z(0)=Z0≥0.r為有毒浮游植物的固有增長率,k為環境對浮游植物的最大承載能力,其中,常數β為浮游動物的最大吸收率,β1為生物量的轉化率,d(>0)為浮游動物的自然死亡率,ρ(>0)為單位生物量的浮游植物產生有毒物質的比率,E(≥0)為捕撈力度,c1(≥0)、c2(≥0)為兩個種群的可捕系數,α(>0)為Holling type Ⅱ函數的半飽和常數[7].由生物學可知,β>β1>0.

另一方面,假設有毒浮游植物生物量的轉化率大于有毒物質的產生比率,即β1>ρ.

在實際生活中,浮游植物、浮游動物的繁殖具有一定的周期性,而人類的捕撈活動也不是時刻不停的,因此離散動力學模型更能反映浮游植物、浮游動物的演化過程.對上述模型進行離散化,可以得到浮游植物、浮游動物捕撈的二維系統如下:

(2)

2 正不動點的存在性

由映射動力系統理論[8]可知,二維動力系統(2)可以寫成一個映射動力系統:

(3)

這里′表示時間增加一個單位.任意時刻的映射T表示空間內的一個點(P,Z)映射到下一個點,則系統的軌道:

Γ(P(0),Z(0))={(P(t),Z(t))|(P(t),Z(t))=Tt(P(0),Z(0))}

是映射T從初始點(P(0),Z(0))開始生成的.

下面求系統(3)的不動點,由于系統(3)的不動點必須滿足P′=P,Z′=Z，因此求系統(3)的不動點即求解下面非線性方程組的解:

(4)

根據方程組(4)的第一個方程可以得到:P=0或

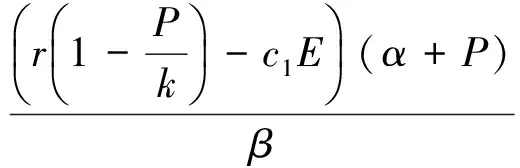
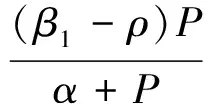
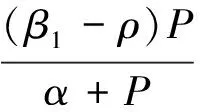
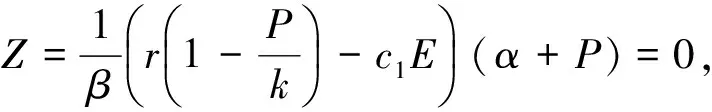
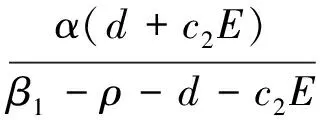
綜合上面的分析可知,關于系統非負不動點我們有下面命題1,

命題1 系統除有一個滅絕不動點S0=(0,0)外,還有如下兩個非負不動點:

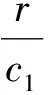
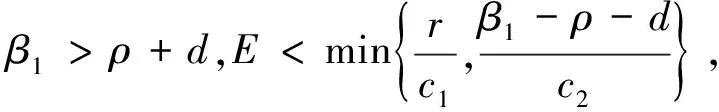
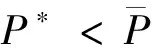
3 不動點的穩定性和分叉

系統(4)在不動點處的局部穩定性取決于其Jacobian矩陣的特征值,在不動點(P,Z)處的Jacobian矩陣有如下形式:

J(P,Z)=

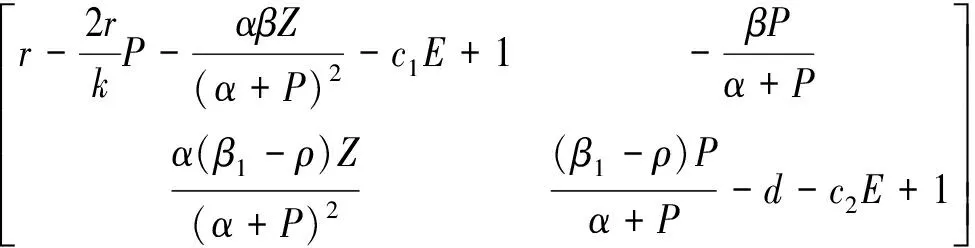
(5)

3.1 滅絕不動點S0=(0,0)的穩定性

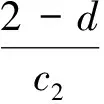
證明在S0=(0,0)處系統的Jacobian矩陣為:

其中J(S0)的特征值為λ1=1+r-c1E,λ2=1-d-c2E.

因為max{|λ1|,|λ2|}<1,即|λ1|<1且|λ2|<1時,(0,0)為漸近穩定的.

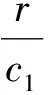
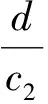
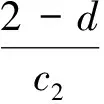
3.2 邊界不動點的穩定性

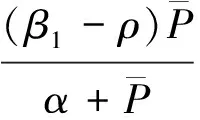
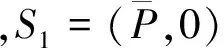
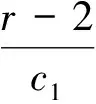
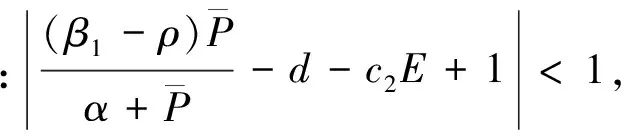
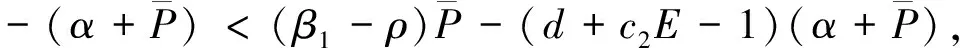
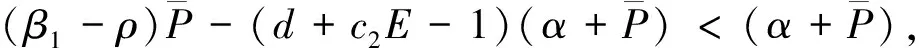
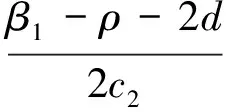
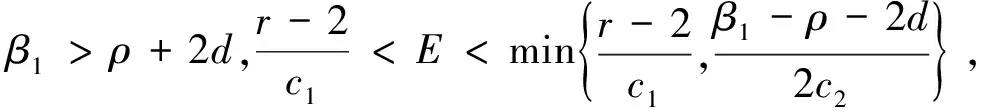
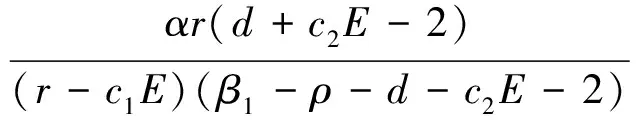
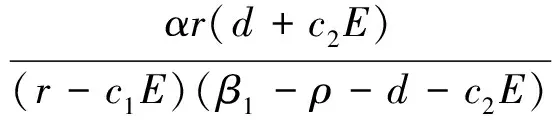
3.3 正不動點S2=(P*,Z*)的穩定性

在S2=(P*,Z*)=

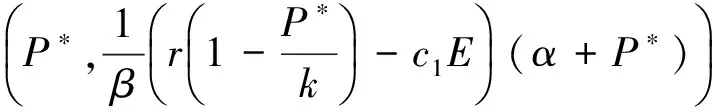
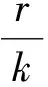
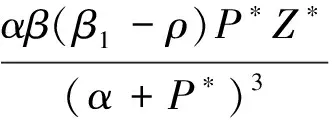
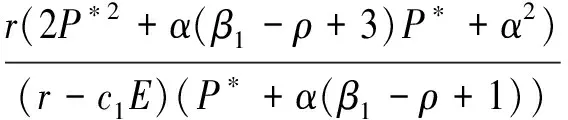
則q2<1成立.

綜合上面的分析,可以得到關于正不動點S2=(P*,Z*)的穩定性和局部分叉定理.

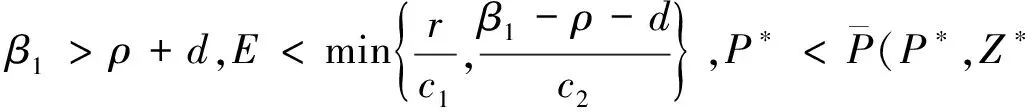
(i)當

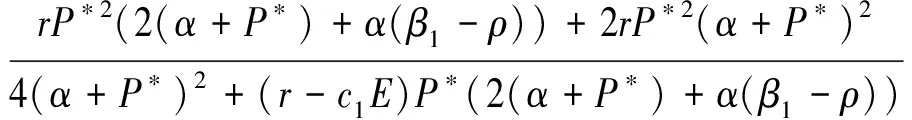
(ii)系統(4)在不動點S2處不可能產生fold分叉;

(iii)當k=

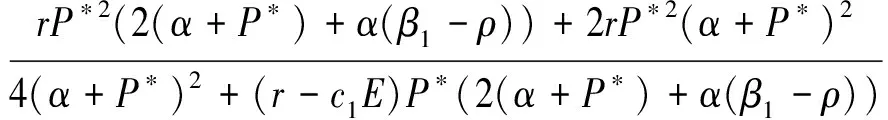
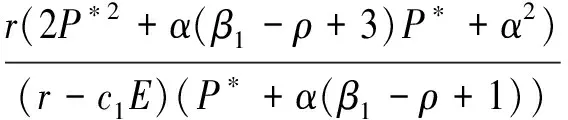
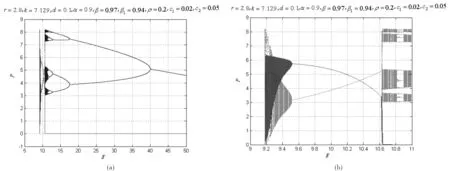
圖1 系統(4)關于捕撈力度E的一維分叉圖

所以系統在S1=(5.0921,0)處Taylor展式(忽略高階余項)為:

(6)

上述方程的矩陣形式為:

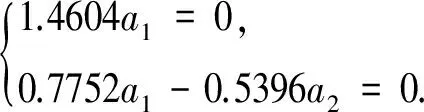
所以映射f1在中心流形上由映射u|→-u+f1(u,h(u)),即u|→-u-0.3928u2+o(u5)給出.

則f1的Schwarzian導數為:

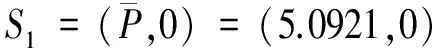
4 結語

本文在假設浮游動物以有毒的浮游植物作為食物,且它們均被人類捕撈的條件下,建立了浮游動物和浮游植物的離散動力學模型,并且對模型進行了非線性分析.我們發現捕撈力度對浮游植物、浮游動物最終的演化有明顯的影響,當捕撈力度過小時浮游植物和浮游動物會出現隨機或準周期波動,過大會發生滅絕,此時對海洋生態環境而言都不是最佳的.存在捕撈力度的某一閾值范圍,此時浮游動植物穩定到一個固定值.當捕撈力度超過某一閾值(例如E>Ec≈10.61)時,相應的以其為食物的較高等浮游動物會滅絕.在單一浮游植物演化中,捕撈力度也有一個較適中的范圍,即過高或過低的捕撈力度均不利于浮游植物資源的可持續利用.

[1]Clark C W.Mathematical bioeconomics:the optimal management of renewable resources[M].New York:Wilery,1976.

[2]Gu Enguo.Nonlinear analysis on the dynamical model of common fishery resource[J].Int J of Nonlinear Sciences and Numerical Simulation,2009,10(5):623-634.

[3]Gu Enguo.Complex dynamics analysis for a duopoly model of common fishery resource[J].Nonlinear Dyn,2010,61:579-590.

[4]Saha T,Bandyopadhyay M.Dynamical analysis of toxin producing phytoplankton-zooplankton interactions[J].Nonlinear Analysis:Real World Applications,2009,10:314-332.

[5]Lü Yunfei,Pei Yongzhen,Gao Shujing,et al.Harvesting of a phytoplankton-zooplankton model[J].Nonlinear Analysis: Real World Applications,2010,11:3608-3619.

[6]Gonzalez-Olivares E,Huincahue-Arcos J.A two-patch model for the optimal management of a fishing resource considering a marine protected area[J].Nonlinear Analysis:Real World Applications,2011,12:2489-2499.

[7]Pei Y,Chen L,Zhang Q,et al.Extinction and permanence of one-prey multi-predators of Holling type Ⅱ function response system with implusive biological control[J].J Theoret Biol,2005,235:495-503.

[8]Bischi G I,Naimzada A.Global analysis of a nonlinear model with learning [J].Economic Notes,1997 (26):143-174.

[9]Jury E I.Inners and stability of dynamic[M].New York: Wiley,1974.

[10]Saber N E.Discrete chaos [M].New York: Chapman & Hall/CRC,2000.