可伸縮中間軸主軸的強度和剛度計算

高龍，劉晟昱，冉振云

(中航工業株洲易力達機電有限公司，湖南株洲412002)

1 概述

這些年，電動助力轉向系統 (Electric Power Steering，EPS)飛速發展，市場對于C-EPS 的操縱舒適性和可靠性的要求也越來越高。這種情況下，對高性能中間軸的需求也在不斷增長，因此對高性能中間軸提出了以下要求:

(1)不會產生沖擊力和異響(這直接導致在花鍵嚙合時產生噪聲，同時也嚴重降低了操作手感);

(2)有很好的剛性，保證其具有比較大的抗扭轉剛度;

(3)具有很低的滑動負載(降低摩擦損耗);

(4)高壽命(要求反撞力能最低限度地增長，接觸面的硬度能最低限度地降低)。

但是這都是建立在優良的強度和剛度的基礎上，現在很多供應商廠家在主軸的結構設計工作有一定的滯后性，使得產品結構更新困難。圖1 為某款中間軸樣件性能曲線。

圖中顯示其抗破壞強度僅為210 N·m，剛度不到15 N·m/ (°)(而產品一般要求破壞強度不小于300 N·m，總成剛度不小于20 N·m/ (°))，對比圖2 的批產合格件曲線圖，很明顯可以發現這是設計中的不足，由此可見，在主軸的定型生產加工前，強度和剛度的設計計算尤為重要。

2 強度計算

2.1 花鍵結構計算

通過扭轉齒根剪切應力的計算推導出花鍵結構的基本尺寸范圍和確定所選用的材料。

齒根彎曲剪應力:

材料的許用拉應力為［δ］，許用扭轉剪切應力為［τ］，屈服極限為δs，強度極限為δb。對于塑性材料，［τ］ = (0.5 ～0.6)［δ］，通常情況下:

其中，n 為安全系數，n≥1。

考慮到通常試驗檢驗要求為破壞強度大于等于Tmax，因此取δb用于計算。

花鍵齒根圓許用扭轉剪切力

［τ］ =0.5δb(取n=1)

而τroot≤［τ］

則有

2.2 主軸強度計算

(1)抗扭截面模量Wt由軸的極慣性矩Iρ來確定

(2)對于復雜截面主軸的極慣性矩的計算則是分別計算每一結構的極慣性矩，然后再疊加計算。

主軸橫截面如圖3 所示，可將其視為實心花鍵軸和滑槽的布爾減運算結果，則其極慣性矩可表述如下:

式中:Iρ1為主軸實心軸極慣性矩;Iρ2為滑槽極慣性矩。

所以

式中:d 為分度圓直徑。

而滑槽的結構簡圖如圖4 所示。O1為主軸花鍵軸軸心，∠AO1C=β;O2為滑槽邊線延長線和滑槽截面中心線交點，∠AO2C=α。則槽截面AEFC 的極慣性矩可表述為:

式中:Iρa是扇面AO1C 的極慣性矩;Iρb是三角形AO1O2的極慣性矩;Iρc是三角形EO2F 的極慣性矩。

于是有:

式中:d 為分度圓直徑。

積分可得:

同理得:

在設計中采用取值代入法(建立參數數據庫)，綜合考慮以得到最適合的截面設計參數。

3 剛度計算

當分析一個階梯軸或者花鍵軸的時候，將其分解成串聯或并聯的圓軸或花鍵軸單體，并確定每個單體的扭轉剛度，然后求出總的扭轉剛度。

(1)并聯軸的總扭轉剛度為各單體剛度的代數和:

(2)串聯軸的總扭轉剛度的倒數為各單體扭轉剛度的倒數代數和:

3.1 圓軸

對于等直徑截面圓軸:

故扭轉剛度

3.2 花鍵軸

花鍵以及帶有鍵槽軸的扭轉剛度可用有限差分法求解圣維南扭轉應力函數求出，得到函數方程:

其中，扭矩系數K 查圖5 可得。

4 實例驗算

以某款樣件作為驗算的參考件，如圖6 所示。

4.1 強度的計算

(1)估算基本尺寸和材料的確定

而Tmax=300 N·m，加工前材料未做前期處理(如調質、正火等)提高強度。

①當使用20 號鋼時，δb=390 MPa，得到Dmin=19.87 mm(可以做較大直徑套筒)

②當使用35 號鋼時，δb=510 MPa，得到Dmin=18.17 mm

③當使用20Cr 時，δb=834 MPa，得到Dmin=15.42 mm(可以做較小直徑主軸)

(2)現在分度圓直徑d =20.79 mm，槽底寬| EF | =2 mm，滑槽槽型角α = 83°，滑槽中心角β = 41.8°，代入式(5)— (11)得:

主軸花鍵軸部分

Iρ=1.436 0 ×10-8m4

主軸實心軸部分

而外花鍵齒根圓直徑為19.8 mm，［τ］ =0.5δb，取35 號鋼時有［τ］ = 255 MPa，即可滿足要求。

套筒內花鍵部分

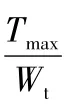
而內花鍵齒根圓直徑為21.9 mm，［τ］ =0.5δb，取20 號鋼時有［τ］ =180 MPa，即可滿足要求。

4.2 剛度的計算

主軸花鍵軸部分B/R=0.075 8，遠小于0.1，查表發現不適用，因此在這種模數很小的情況下，還是采用擬合計算的方法得到極慣性矩再計算剛度。

(1)C1是主軸實心圓軸部分的剛度，由式(12)可得

花鍵軸部分剛度

綜合式(5)— (13)可得:

Iρ21=1.436 0 ×10-8m4

C21=35.900 ×103N·m/rad

C23=36.470 ×103N·m/rad

d=19.7 mm 時，代入式(11)得到:

Iρ22=1.086 4 ×10-8m4

故C22=72.427 ×103N·m/rad

得C2=14.476 ×103N·m/rad

CS=7.51 ×103N·m/rad (設計參考)

然后再得到套筒的各段剛度，以及萬向節組合的剛度就可以計算出中間軸的基本剛度值。

(3)套筒分為三段，花鍵部分偶合段，花間部分非偶合段，尾部套筒段。它們對應的剛度分別是C31、C32、C33。由于套筒內部開有三道滾道，計算采用花鍵底徑擬合運算其極慣性矩。

內花鍵部分

尾部套筒部分

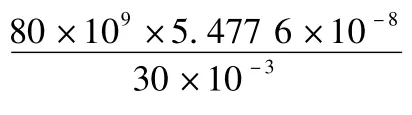
(4)可由結構并、串聯關系求得中間軸除萬向節叉組合的剛度CZ。

得到CZ=10.151 ×103N·m/rad =181.4 N·m/ (°)(有較大的剛度余量)

(5)由試驗測試和相關計算顯示中間軸萬向節叉組合的剛度一般能達50 N·m/ (°) (萬向節叉組合的剛度對整體剛度影響很大)。

故中間軸的總體剛度:

得到CS=21.97 N·m/ (°)，滿足要求。

【1】ISAKOMER Robert I. Machine Design［M］. Torsional Rigidity of Composite Shates，1983.

【2】SOFRONAN T. Case 21:Analyzing a Spline Failure:Torsional Spline Failures are Telling you Something［J］. Hydrocarbon Processing，2004，83(6).

【3】UEDA h.Technical Trends Regarding Intermediate Shaft in Steering Systems［J］.Koyo Engineering Journal，2005，168.

【4】孫小偉.漸開線齒輪花鍵冷擠壓工藝研究［D］.吉林:長春理工大學，2002.

【5】張興旺. 花鍵冷滾壓工藝與實驗研究［D］. 山西:太原科技大學，2009.