基于模態疊加法振弦傳感器激振力優化分析

申 展，馬少杰，張 合

（南京理工大學 機械工程學院，江蘇 南京 210094）

0 引言

振弦傳感器激振力長期高頻率作用于振弦上，該力的合理與否直接影響了振弦式傳感器的長期穩定性和壽命，所以激振力大小的設計對于振弦式傳感器至關重要。目前國內振弦式表面應變傳感器技術日趨完善，但是國內生產的振弦傳感器與國外生產的振弦傳感器相比，在傳感器長期穩定性方面的技術還不夠成熟，尤其是激振線圈產生的激振力的設計，基本憑借經驗公式和試驗，很少利用CAE 分析不同激振力激振后振弦的振動響應。為了提高振弦傳感器的長期穩定性和壽命，得到最優激振力，本文利用ANSYS模態疊加法對振弦振動響應進行仿真分析。

1 振弦激振拾振原理

1.1 振弦激振原理

激勵振弦振動的目的是測出振弦振動的頻率，本文采用單線圈激振法，具體過程如下：由單個線圈進行激振和拾振，將拾到的振動信號傳給采集儀，由采集儀對采集信號進行整形、放大等處理，最后輸出對應的頻率信號。

1.2 振弦拾振原理

振弦激振后振動，由于振弦被置于磁場中，因此它在振動時在電磁線圈中產生感應電動勢V，感應電動勢V 的頻率就是振弦振動的頻率，所以其響應信號是一定頻率的正弦信號。但是由于振弦傳感器的金屬外殼不可能完全實現密封，其中的空氣阻力以及鋼弦兩端緊固夾頭的作用力將使振弦振動的振幅和能量逐漸減小。因此，振弦的響應信號是按指數函數衰減的阻尼振動信號。其振動表達式為：

其中：β為表征鋼弦所受到阻尼大小的阻尼系數；A0為初始振幅；φ0 為初始相位；ω 為角頻率。

振弦激勵響應信號的波形圖如圖1 所示。圖1中，t0為振動響應初期時間，該時間段內頻率信號不穩定；t2為振動響應后期時間，該時間段振動幅值過小，不易采集到信號；故一般取中間段振弦響應時間，即t1時間段。

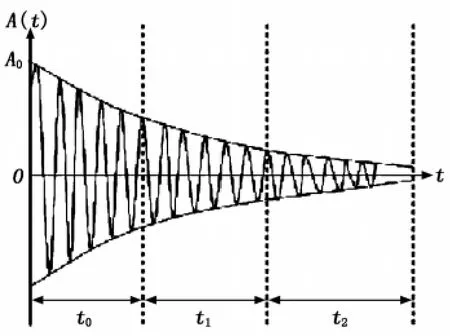
圖1 振弦激勵響應信號波形

振弦式傳感器測頻方法主要有兩種：計數法和多周期測量法。計數法是在單位時間內對被測信號脈沖進行計數；多周期測量法是用計數器測量多個周期值。

2 ANSYS模態分析振弦基礎頻率處振動響應

本文采用某型號手持振弦數據采集儀，該型號采集儀采用掃頻激振方式，激勵電壓為30V 的脈沖電壓，要求傳感器感應電動勢持續時間≥500ms，感應電壓≥0.05mV。

2.1 對振弦施加預應力

建立直徑Φ0.2 mm、長度L＝90 mm 的振弦模型。當振弦加載上64N 的預壓力后，振弦繃緊，同時被拉長了約0.928 9mm，此時繃緊的振弦的固有頻率f 可由振弦數學模型計算：

其中：L 為振弦長度；σ為振弦內應力；ρ為振弦密度。

將L＝90mm，σ＝2 229.30 MPa，ρ＝7.85g／cm3代入式（3）可計算出此時振弦的固有頻率f ≈2 960.580 1Hz。

2.2 振弦模態分析

在模態分析過程中選擇開啟預應力影響，將上一步完成的預應力靜態分析結果加載到模態分析過程中。

ANSYS模態仿真分析得出的振弦模型的固有頻率f＝2 978.1 Hz，與理論計算得到的振弦固有頻率f≈2 960.580 1Hz數值基本一致，進一步驗證了仿真分析的精確性以及模型建立的合理性。

2.3 振弦模態疊加振動響應分析

完成預應力加載的靜態分析和振弦6階模態分析后，繼續對振弦進行模態疊加分析。運用模態疊加分析來確定振弦承受隨時間變化的脈沖激勵載荷時振弦的動力學響應。

在振弦中間節點22施加一個Y 正方向的脈沖力F＝0.01N，脈沖力持續時間t＝33.5μs（與振弦固有振動周期T 相同）。將該脈沖力F＝0.01 N 以f＝2 978.1Hz的頻率加載在振弦上，加載45 個周期脈沖力，振弦達到共振，振動幅值和振動時間的關系如圖2所示。

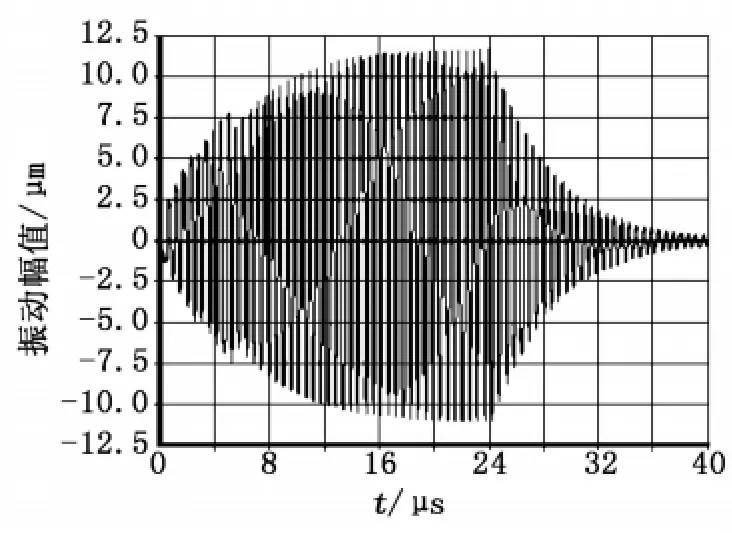
圖2 振動幅值與振動時間關系曲線

改變脈沖力的大小，得到不同激振力激振線圈在不同振幅處的振動響應時間，見表1。表1中，A 為該激振力對應的最大振幅幅值。由表1可以看出，激振力的大小變化對振弦振動響應時間的影響較小。對振弦振動幅值的大小影響較大，即影響了振弦內應力的大小，最終影響了振弦式傳感器的長期穩定性。當F≥0.06N 時，振幅在0.1×107mm 滿足線圈振動響應時間≥500ms的要求。

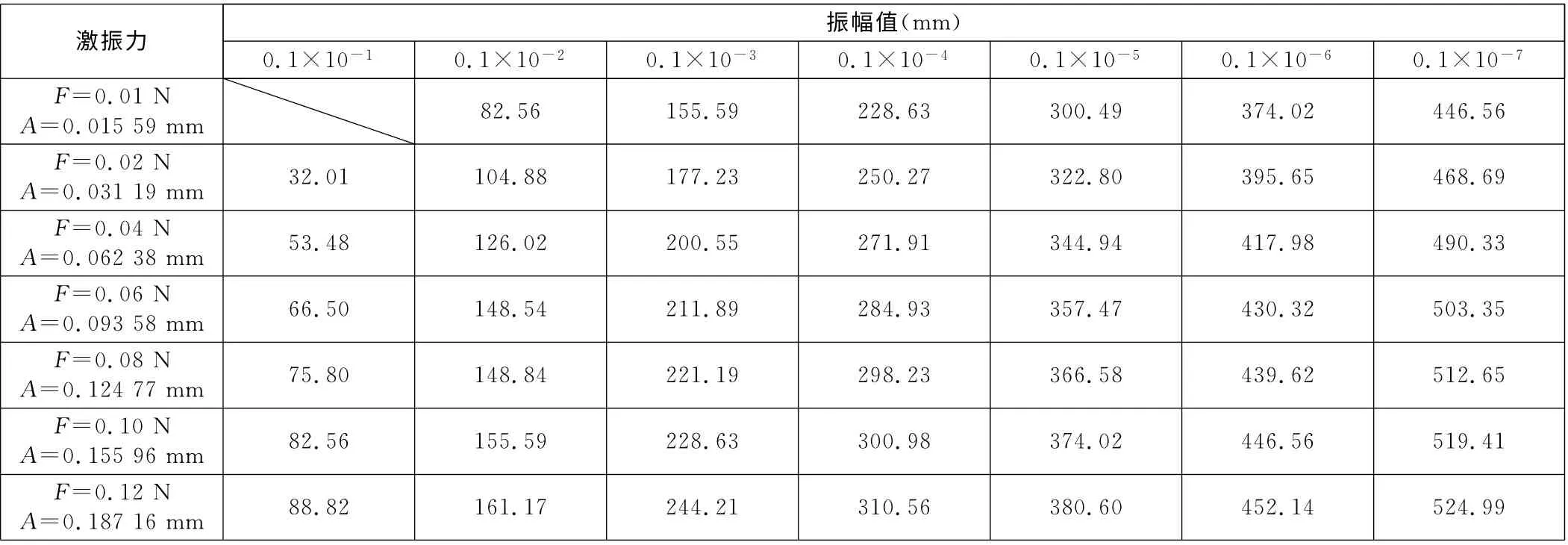
表1 不同激振力激振線圈在不同振幅處的振動響應時間 ms

3 磁場強度對線圈感應電動勢的影響

當振弦振動時，影響了線圈內部的磁場分布，從而使得線圈產生感應電動勢，由法拉第電磁定律可得感應電動勢E：

其中：N 為線圈匝數；S 為線圈橫截面積；Δφ 為磁通變化量；ΔB 為磁感應強度變化量；Δt為時間變化量。

如果加大磁場，即加大了線圈內部的磁感應強度，對于同一振動幅度，磁場越強，線圈感應電動勢越明顯，值越大，持續時間也越長。建立模型，模型包括一個直徑Φ8mm、厚度1 mm 的強磁線圈、鐵心、空氣、振弦，圖3為振弦初始狀態磁場分布。圖3中，黑色方形線框為鐵心，線圈中磁感應強度的變化主要來自于鐵心內部磁感應強度的變化。永磁體產生的磁場主要集中在振弦中；圖3 中黑線sz 為定義的一條閉合路徑，在該路徑上對磁感應強度B 進行積分，即得到線圈內部磁通量大小；圖3中振弦內部磁感應強度最大值Bmax＝9.207×103T。

圖4 為定義路徑上的磁感應強度曲線。經過ANSYS后處理POST1中的閉合路徑積分命令，將電磁感應強度在閉合路徑sz上積分，最終得到線圈內部電磁感應強度Bmax＝3.497 7×103T。

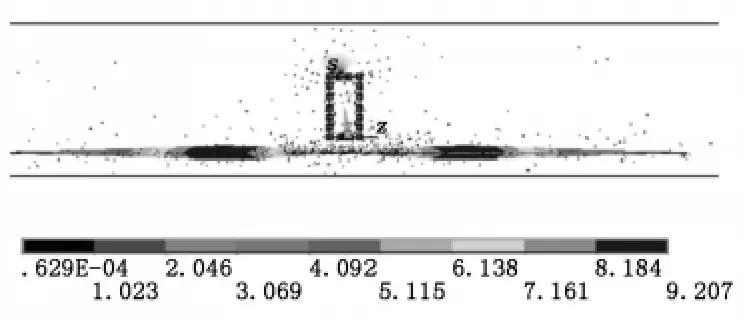
圖3 振弦初始狀態磁場分布

以上分析為振弦處在靜止狀態時的磁場分布情況。同理可得當振弦的振動幅值（mm）為0.1×10－1、0.1×10－2、0.1×10－3、0.1×10－4、0.1×10－5、0.1×10－6、0.1×10－7位置處線圈內部電磁感應強度B 的數值，根據公式（4）可以計算出線圈的感應電動勢，具體見表2。

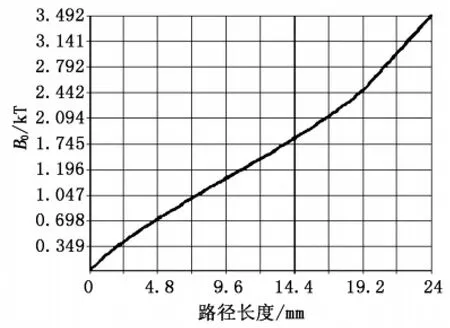
圖4 定義路徑上的磁感應強度曲線

表2 不同振動幅度對應線圈電磁感應強度和感應電動勢

由表2可以看出：振弦振幅越小，線圈感應電動勢越小；在振弦振動響應幅值≥0.1×10－7mm 處，線圈感應電動勢均能滿足E≥0.05mV。

4 結論

（1）激振力的大小變化對振弦振動響應時間的影響較小，對振弦振動幅值的大小影響較大，即影響了振弦內應力的大小，最終影響了振弦式傳感器的長期穩定性。

（2）影響線圈振動響應持續時間最主要的因素為線圈所處電磁場的強度。

［1］ 鄧鐵六.高準確度振弦式傳感器研究［J］.山東科技大學學報，2010（1）：52－57.

［2］ 徐承軍.振弦式傳感器動態測試機理研究［J］.儀表技術與傳感器，2011（12）：98－102.

［3］ 張心斌.振弦式應變傳感器特性研究［J］.傳感器世界，2003（8）：19－21.

［4］ 崔軍輝.提高振弦式傳感器測量精度的方法的研究［J］.傳感技術學報，2009（9）：1276－1279.

［5］ 江修.振弦式傳感器的頻率敏感機理與應用［J］.傳感器技術，2003（12）：22－24.

［6］ Petrovsky，Myron.Instrumentation monitoring of small hydroelectric dams［G］／／Proceedings of the American Power Conference.［s.l.］：［s.n.］，1989：1015－1020.

［7］ Feng Yu，Naren Gupta.An efficient model for improving performance of vibrating－wire instrument［J］.Measurement，2005，37：278－283.

［8］ 王化祥.傳感器原理及應用［M］.天津：天津大學出版社，1997.

［9］ Sreeshylam P.Condition monitoring of Prestressed concrete structures using vibrating［J］.International Journal of COMADEM，2008（3）：46－54.