漸開線圓柱齒輪齒根彎曲應力精確計算

姚和川，王明明，李 鳴，孫淑霞

（1.沈陽新松機器人自動化股份有限公司 激光事業部，遼寧 沈陽 110168；2.沈陽工業大學 機械工程學院，遼寧 沈陽 110870）

0 引言

齒輪傳動是機械傳動中應用最廣泛的一種形式，具有傳動比準確、效率高、結構緊湊、工作可靠、壽命長等優點。齒輪最常見的失效形式為齒根彎曲疲勞應力引起的輪齒折斷和齒面接觸疲勞應力引起的齒面點蝕，而輪齒折斷是最嚴重的失效形式，并且常常會突然發生，導致整臺機器甚至是生產線停車、停產。因此在齒輪的設計過程中需要精確計算齒根的彎曲疲勞應力，而計算齒根彎曲疲勞應力的經典理論算法不僅需要進行大量的簡化，還需要對計算結果進行修正［1－4］。本文采用ANSYS 軟件建立齒輪齒廓曲線和齒根曲線，然后精確計算齒輪的齒根彎曲應力和齒面接觸應力，并與理論方法的計算結果進行對比。

1 齒輪模型

1.1 漸開線齒廓曲線建模

如圖1所示，當一條直線在圓周上作純滾動時，直線上任意一點的軌跡稱為該圓的漸開線，這個圓稱為漸開線的基圓，其半徑用rb表示；直線BK 稱為漸開線的發生線；K 為漸開線上的任意一點，其向徑用rK表示，漸開線AK 段的展角用θK表示；漸開線在K 點的壓力角用αK表示。則漸開線的極坐標方程為：

將式（1）轉化為直角坐標方程為：

其中

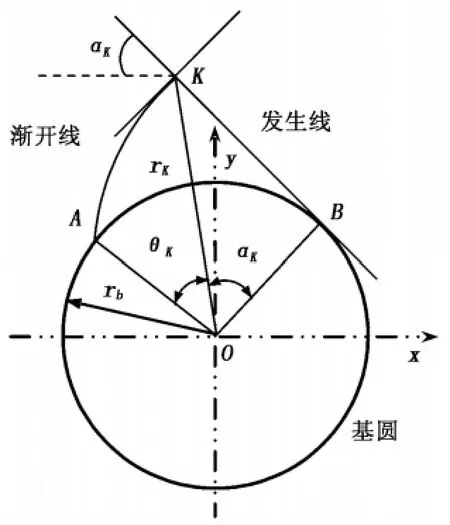
圖1 漸開線的形成

1.2 齒根過渡曲線的建模

盡管過渡曲線在齒輪工作中不參與嚙合，但是它卻對齒輪根部的彎曲應力有著重要的影響，精確地繪制齒輪根部過渡曲線是進行齒輪根部彎曲應力有限元分析的先決條件。齒根過渡曲線形狀取決于兩個因素：一是刀具與齒坯的相對運動關系（加工方法）；二是刀具頂部的刃形。齒輪加工方法不同或采用刀具不同，加工出的齒根過渡曲線則不相同。即使采用同一種加工方法用同一類刀具加工，若切齒刀具的齒頂圓角半徑不同，所得到的齒根過渡曲線也不相同［5，6］。

滾刀加工齒輪時，如果刀具齒廓的頂部具有兩個圓角，則切出的齒根過渡曲線如圖2所示，I、II兩段為延伸漸開線的等距曲線，III段為齒輪的根圓圓弧。

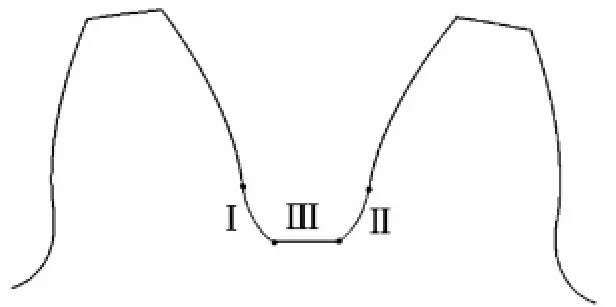
圖2 第一類齒根過渡曲線

圖3為雙圓角刀具的基準齒形，其參數的關系式為：

其中：a 為刀具圓角中心到中線的距離；h＊a為齒頂高系數；m 為模數；c＊為頂隙系數；α 為壓力角；b為刀具圓角部分的高度；r0為刀具齒頂的圓角半徑。

圖3 雙圓角刀具的基準齒形

該過渡曲線的參數方程式為：

1.3 齒輪有限元模型

用上述方法建立的一對相嚙合齒輪的有限元模型如圖4所示，其參數為：模數m＝4 mm，壓力角α＝20°，小齒輪齒數Z1＝21，大齒輪齒數Z2＝45，齒寬h＝25mm，扭矩T＝4 988N·mm。

圖4 嚙合齒輪的有限元網格模型

2 計算結果及分析

圖5為兩個齒輪的接觸狀態。此時兩齒輪在節點處嚙合，嚙合點隨齒輪轉動發生變化。計算發現：在小齒輪轉過0°～1.7°時第一對齒嚙合，在14.25°～17.14°為第二對齒嚙合，在1.7°～14.25°為兩對齒同時嚙合，小齒輪轉角1.7°為單齒嚙合的極限位置，此時齒根彎曲應力達到最大值，圖6為齒根部位應力分布圖。

圖5 兩齒輪的接觸狀態

圖6 齒根部位應力分布

齒根彎曲應力的經典理論公式為：

其中：U 為載荷系數，取U＝1；d1為小齒輪的分度圓直徑，d1＝84mm；YFa、YSa、Yε分別為齒形系數、應力修正系數和重合度系數，由參考文獻［5］查圖得到YFa＝2.8，YSa＝1.56，Yε＝0.69。將已知參數代入式（7）計算得σF＝89.1 MPa。

可見，理論方法的計算結果在修正前（修正前為29.7 MPa）與有限元計算結果（67.649 MPa）相差甚遠，修正后的值（89.1 MPa）略大于有限元計算結果。兩者的差異主要是理論方法在計算齒根應力時做出如下簡化：①把漸開線齒廓簡化為等截面梁；②對加載點和危險截面位置進行了簡化；③忽略了由載荷Fn的水平分量Fncosα產生的剪應力和垂直分量Fnsinα 所產生的壓應力，只按齒根危險截面的彎曲應力進行計算；④修正系數本身沒有理論依據，存在較大的近似性。

3 結論

利用有限元軟件可以精確建立漸開線和齒根曲線的真實形狀，用接觸單元可以計算出單齒嚙合區和多齒嚙合區。計算齒輪在單齒嚙合區的極限位置嚙合時齒根的應力分布，得到周期性最大彎曲疲勞應力。理論方法的計算結果在修正前與有限元計算結果相差甚遠，修正后略大于有限元計算結果，兩者的差異主要是由于理論方法的計算簡化引起的。

［1］ 武志斐，王鐵，張瑞亮.18Cr2Ni4WA 齒輪彎曲疲勞試驗及基于可靠度的試驗數據統計研究［J］.機械強度，2012（1）：154－158.

［2］ 林騰蛟，沈亮，趙俊渝.風電增速箱輸出級齒輪副疲勞壽命有限元分析［J］.重慶大學學報，2012（1）：1－6.

［3］ 韓志武，呂尤，牛士超.仿生表面形態對齒輪彎曲疲勞性能的影響［J］.吉林大學學報，2011（3）：702－705.

［4］ 何曉華，陳兵奎.齒條型刀具對齒輪彎曲疲勞強度的影響分析［J］.機械傳動，2011（7）：58－61.

［5］ 吳繼澤，王統.齒根過渡曲線與齒根應力［M］.北京：國防工業出版社，1989.

［6］ 楊慶詳，趙言輝.滲碳及滲碳噴丸齒輪輪齒彎曲疲勞極限的定量分析［J］.機械工程學報，2004，36（8）：39－42.