機匣靜葉耦合振動分析的有限元建模方法研究

孫陽， 王克明， 張婷婷

（沈陽航空航天大學航空航天工程學部，沈陽110136）

1 引 言

振動破壞是航空發動機常見的破壞形式之一，因此，振動分析是其結構分析的重要組成部分。航空發動機的靜子系統是支承系統，對其振動固有特性分析即模態分析是必要的。有限元模型的簡化是有限元分析的關鍵步驟，在滿足精度要求的前提下，合理的簡化有限元模型可進行便捷快速的有限元計算。懸臂葉片連同機匣的靜子結構是發動機靜子系統的典型結構，分析機匣與葉片的耦合振動是非常重要的，對此典型結構的周向彎曲振動進行了有限元建模方法研究，采用三種建模方法并根據計算結果做出對比分析。

2 結構的幾何模型

選取某型航空發動機壓氣機處的一圈靜子葉片和與葉片連接的一小段機匣為研究對象，計算結構的周向彎曲模態頻率和振型。建模時將機匣簡化為等厚的薄壁圓柱殼，考慮結構中懸臂葉片以彎曲振動為主，根據葉片截面等效質量和截面等效彎曲剛度的原則將葉片簡化成變矩形截面板，滿足了等效質量和等效剛度。葉片尺寸小但數量多，葉片沿機匣周向均勻地分布，保留葉片與機匣的安裝角度。初步化簡后的結構如圖1，機匣和葉片的尺寸如圖2。

圖1 結構的幾何模型

圖2 結構的尺寸

3 結構的三維實體有限元模型及振動模態分析

3.1 結構的三維實體有限元模型

采用三維實體單元建模可以最真實地反映結構的幾何特性，通過實體單元計算得到的結果也是最準確的。模型采用六面體網格劃分，采用比較密集的網格，使每個單元的尺寸相對較小，這樣通過計算模態分析可以得到較為準確的頻率和振型。

3.2 實體單元建模的振動模態分析

在進行模態分析之前，約束了機匣截面一端沿發動機中軸線方向的位移，這樣可以得到較為單一的周向彎曲頻率和振型，避免了振型中夾雜著結構扭轉和其它方向彎曲的變形。單元類型選擇solid45，結構的有限元模型如圖3。

圖3 實體單元建模的局部有限元模型

模態分析參數為：彈性模量E＝210000N/mm2、密度ρ＝7.85×10-9t/mm3、泊松比μ=0.3。經ANSYS 軟件計算并得到模態頻率如表1 中①，前5 階彎曲振動振型如圖4。由圖4 可知，振型為機匣的的周向彎曲，振型呈花瓣狀，隨著模態頻率的升高，花瓣形狀變小，花瓣數量增多。

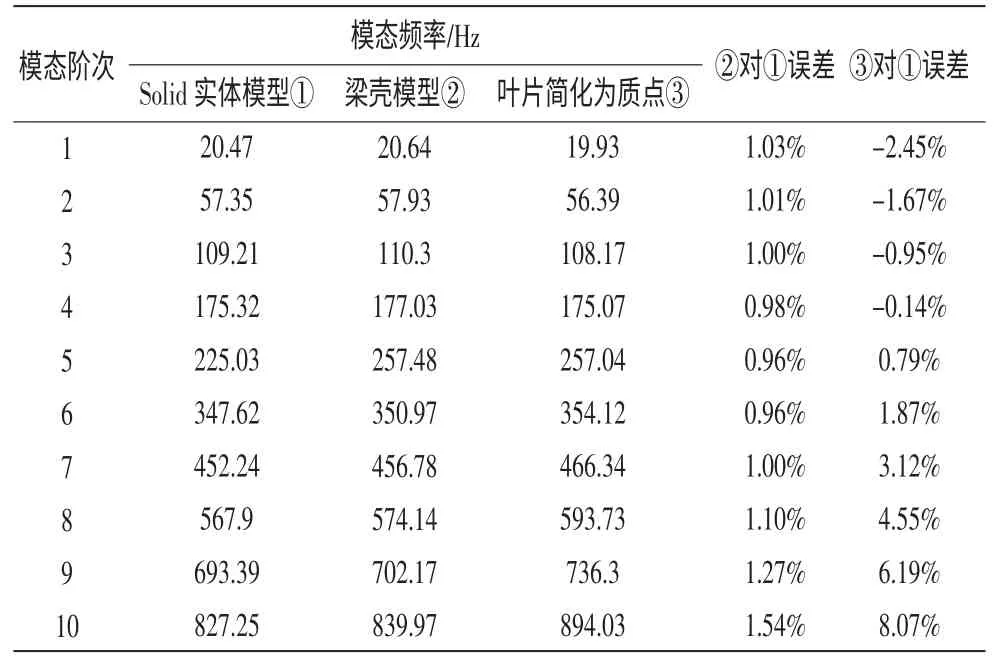
表1 三種有限元模型得到的模態頻率匯總

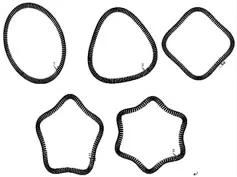
圖4 實體單元有限元模型的振型

4 使用梁、殼單元簡化結構的有限元模型

4.1 梁、殼單元建立葉片、機匣的有限元模型

根據模型的結構特點，機匣是薄壁結構，可以用殼單元shell63 通過定義殼的厚度來處理；葉片經初步處理后已經簡化為變矩形截面板，沿葉片的展向用若干個一維梁單元beam188 建立階梯梁來處理，分別定義梁單元的截面形狀。在機匣上標記葉片連接的區域，梁殼單元的局部模型如圖5。

模態分析中兩個關鍵因素為彈性和慣性，通過觀察結構及結構的模態振型，結構的彈性主要以機匣的周向彎曲變形為主，在低階模態分析中葉片的彎曲剛度遠大于機匣的周向彎曲剛度，葉片主要貢獻了慣性，但考慮葉片和機匣的連接，機匣上葉片和機匣的連接處抗彎剛度增大。

圖5 梁殼單元有限元的局部模型

4.2 梁殼單元的連接

圖6 采用mpc184 單元的梁殼連接方式

直接采用梁殼共用節點的有限元模型并不能準確地進行梁殼的連接，因此引入mpc184 單元，即在梁與殼的連接處建立剛性較大的梁單元來實現梁殼連接。通過此單元建立的連接有多點約束的作用，使梁單元末端節點與殼網格上葉片同機匣連接位置的幾個關鍵節點建立多點耦合約束關系，確保了連接處力與力矩的正確傳遞，完成梁殼的連接。mpc184 單元的連接方式如圖6。梁殼單元建模的有限元模型如圖7，進行模態分析后得到模態頻率見表1 中②，振型如圖8。

圖7 梁殼單元建模的有限元局部模型

圖8 梁殼單元有限元模型的振型

5 質量單元對葉片的簡化

由分析可知：結構的周向彎曲振動中，主要以機匣的彎曲彈性變形為主，葉片則主要貢獻了質量（即慣性）。引入mass21 單元，可將葉片簡化為其質心位置的質量單元，并剛性連接于對應的機匣位置，結構簡化后的有限元模型如圖9。由圖9 可知，簡化后模型極為規整，劃分的網格質量高、數量少。這樣的建模方法忽略了葉片和機匣的連接對機匣彎曲剛度的增加，同時將葉片自身視為完全剛性。這種簡化方法并不能在振動分析中等效剛度，但是此結構的葉片尺寸短小，葉片與機匣的連接面積也很小，在相對重要的低階彎曲振型中，葉片的連接對機匣剛度的增加并不大。在低階振動中，葉片難以產生彎曲振動，可以將其看作剛體。因此，采用上述做法是可行的。通過計算可得模態頻率見表1 中③，振型如圖10。

圖9 質量單元代替葉片的有限元局部模型

圖10 質量單元代替葉片的有限元模型的振型

6 計算結果的對比分析

觀察三種建模方法得到的振型，振型是完全一致的。分析比較三種建模方法通過計算得到的模態頻率見表1，將實體網格建模的有限元模型的模態頻率作為標準，其它兩種方式與其比較，得到相對誤差。由表1 可知，梁殼模型的相對誤差無論在低階還是高階模態頻率中誤差都很小且保持穩定。在葉片簡化為質量單元的模型中，低階模態頻率的相對誤差較小，高階模態頻率的誤差偏大。

7 結 論

（1）實體單元有限元模型計算準確，受但限于模型尺寸，通常計算規模很大。

（2）梁殼模型大量減小了網格數量，正確處理好梁殼的連接可以得到較為準確的計算結果。

（3）通過質量單元模擬葉片，有限元的計算規模也是最小的。從上述的分析可知：低階模態頻率的計算結果相對準確，高階模態頻率的計算結果誤差偏大。

［1］ 金基鐸，王克明.機械振動基礎［M］.沈陽：沈陽航空工業學院，2001.

［2］ 劉鴻文，林建興，曹曼玲，等.材料力學［M］.北京：高等教育出版社，2004.

［3］ 冷紀桐，趙軍，張婭，等.有限元技術基礎［M］.北京：化學工業出版社，2007.

［4］ 謝元丕，馮剛.ANSYS 三維實體單元與板殼單元的組合建模研究［J］.機械設計，2009，26（4）：5-7.

［5］ 謝最偉，吳新躍，萬強.有限元中體殼單元的耦合問題研究［J］.機械設計，2011，28（3）：91-93.