MPPT不調節母線電源系統穩定性分析

林文立 劉治鋼 余恒

（北京空間飛行器總體設計部，北京 100094）

1 引言

最大功率點跟蹤（MPPT）控制技術已經在國外多個低軌大功率衛星、電推進等衛星平臺及深空探測器上得到越來越多的應用［1-2］，例如歐洲航天局的“火星快車”（Mars Express）、“金星快車”（Venus Express）［3］、羅塞塔號（Rossetta）［4］、信使號（Messenger）［5］、貝皮-科倫坡（Bepi-Colombo）［6］等均采用串聯型MPPT 電源系統。然而，由于功率源與負載均為非線性，串聯型MPPT 電源系統在太陽電池陣與太陽電池陣功率調節器（Array Power Regulator，APR）間存在母線電壓振蕩或跌落等不穩定現象［7］。文獻［8］利用簡化電壓控制模型，對雷達衛星-2（RADARSAT-2）及 宇 宙-地 中 海（COSMOSkyMed）衛星電源電壓控制環的穩定性進行了分析，具有一定代表性；而國內目前對于空間電源系統母線電壓穩定性的研究還比較少。

本文提出一種MPPT 不調節母線電源系統拓撲結構，介紹了它的兩域控制模式，建立了太陽電池陣源端與負載端穩態分析的等效電路模型，采用小信號等效分析方法，對系統穩定性進行分析，研究結果可為MPPT 控制技術在未來空間電源系統中應用提供設計參考。

2 電源系統拓撲及控制模式

圖1所示為MPPT 不調節母線電源系統拓撲，主要由太陽電池陣、APR、控制電路、蓄電池組、負載等組成。根據發電端及負載端電壓高低，APR 主電路可選擇升壓（或降壓）直流-直流（DC-DC）變換器形式。其中，Ⅰload為負載電流；Ⅰbatt為蓄電池充／放電流；isa為太陽電池陣輸出電流；vsa為太陽電池陣輸出電壓；vMEA為一次電源母線電壓。

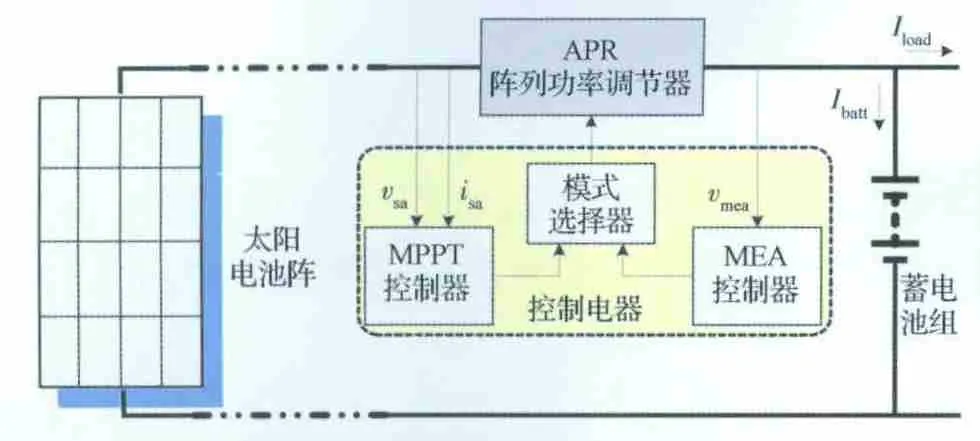
圖1 MPPT 不調節母線電源系統拓撲Fig．1 Diagram of MPPT unregulated bus electrical power system topology

圖1中，控制電路包括MPPT 控制器、主誤差信號放大器（Main Error Amplifier，MEA）控制器、模式選擇器等，通常設計為兩域控制方式［9］，如圖2所示，其中電壓Va＜Vb＜Vc＜Vd，模式選擇器根據負載功率需求及母線電壓高低自主選擇MPPT 控制模式或者MEA 控制模式，具體描述如下：當母線電壓處于（Va，Vb）范圍內，即負載功率需求大于太陽電池陣所能提供的電能時，模式選擇器選擇MPPT 控制模式，電源系統工作在MPPT 控制域，太陽電池陣始終跟蹤最大功率點輸出；當母線電壓處于（Vc，Vd）范圍內，即太陽電池陣所提供電能大于負載功率需求時，模式選擇器選擇MEA 控制模式，系統處于充電及電壓控制域，控制電路根據電池充電特性調整母線電壓值，當電池電壓充滿電后進行恒壓控制，在此域范圍內太陽電池陣根據負載及電池充電需要調整輸出功率；（Vb，Vc）電壓范圍是控制系統所設置的遲滯區間，以避免在兩種模式間頻繁切換。

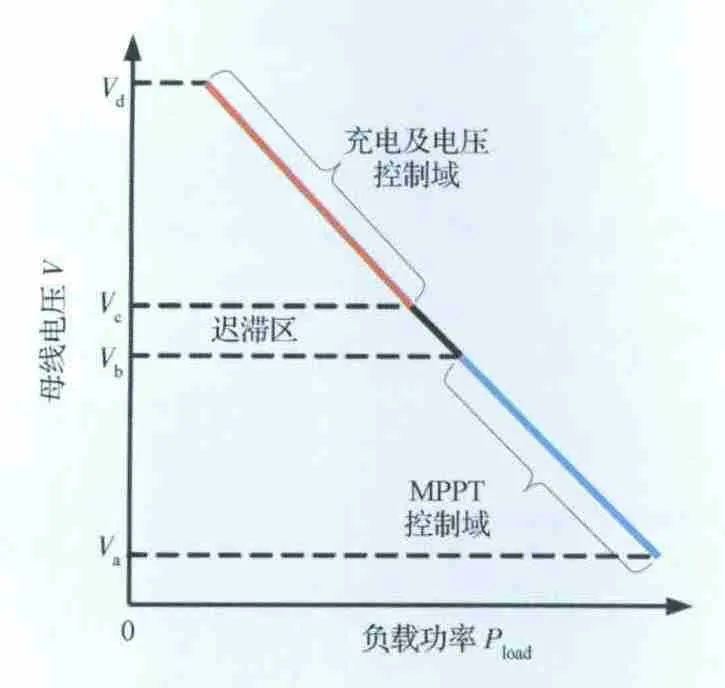
圖2 MPPT 不調節母線電源系統的兩域控制模式Fig．2 Two-domain control mode for MPPT unregulated bus electrical power system topology

3 電源系統穩定性分析

上文提到MPPT 不調節母線電源系統存在兩域工作模式，因此，下面將分別針對兩種工作模式進行電源系統的穩定性分析。

3．1 MPPT控制域下電源系統穩定性分析

在MPPT控制域下，太陽電池陣輸出電壓始終保持在最大功率點對應的電壓值附近，因此APR 的輸入端可認為是一個恒壓源。圖3（a）中太陽電池陣輸出特性曲線與APR的輸入特性（恒壓源）曲線二者交點即為暫態工作點，建立MPPT 控制域下的等效電路模型，如圖3（b）所示，圖中左側函數f（vsa）代表太陽電池陣的輸出特性，vsa為太陽電池陣的輸出電壓，isa為太陽電池陣的輸出電流，電容Csa為太陽電池陣寄生電容，Lline為線路寄生電感，iL為電感電流值，APR及后級負載均統一用恒壓源VAPR代替，見圖3（b）中右側方框，其函數表達式為f（iL）。

根據圖3（b），得到如下表達式：

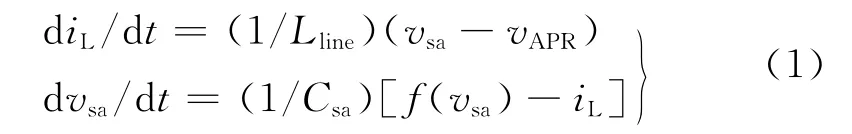
由于f（vsa）為非線性函數，設圖3（a）中暫態工作點處電壓穩態值為vsa，在此處添加小信號動態擾動值Δvsa，按泰勒級數的一階線性展開［10］，得

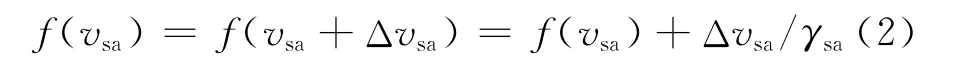
式中：γsa表示函數f（vsa）在某一特定太陽電池陣輸出電壓數值vsa時的微分值，因此，γsa＜0。

將式（2）代入式（1），得到其在暫態工作點處小信號線性狀態空間表達式為

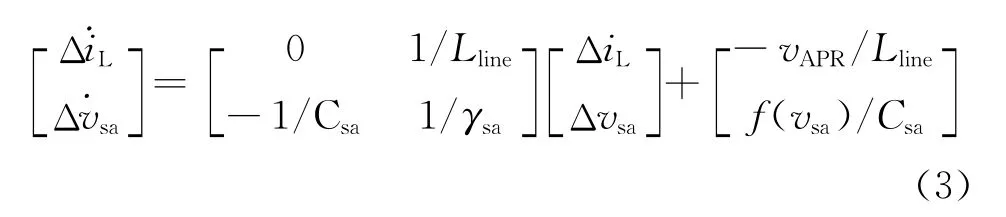
經計算，得到式（3）的特征根為

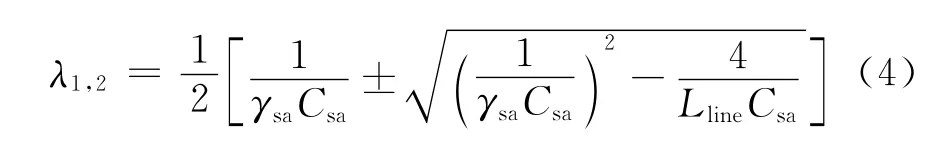
由于γsa＜0，因此式（4）中兩個特征根λ1，2均為負值，根據李亞普諾夫穩定性定理［11］可知，該線性定常系統是穩定的，從而表明MPPT 不調節母線電源系統在MPPT 控制域下始終是保持穩定的。

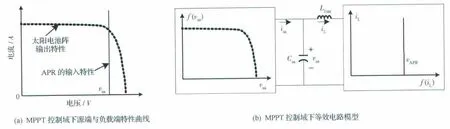
圖3 MPPT 控制域下源端與負載端特性曲線及穩態分析等效電路模型Fig．3 Source and load characteristics curves and stability analysis equivalent circuit model in MPPT control domain

3．2 充電及電壓控制域下電源系統穩定性分析

在充電及電壓控制域下，對一次母線進行恒壓控制，因此，APR 的輸入端呈現恒功率特性。圖4（a）為充電及電壓控制域下源端與負載端特性曲線，其中太陽電池陣輸出特性曲線與APR 的輸入特性（恒功率）曲線二者交點即為暫態工作點，建立充電及電壓控制域下的等效電路模型，如圖4（b）所示，圖中APR 及后級負載均用恒功率特性曲線代替，見圖4（b）中右側方框。

圖4 充電及電壓控制域下源端與負載端特性曲線及穩態分析等效電路模型Fig．4 Source and load characteristics curves and stability analysis equivalent circuit model in charging and voltage control domain

根據圖4（b），得到如下表達式：

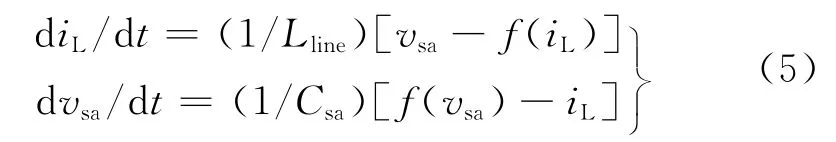
其中，f（vsa）、f（iL）均為非線性函數，設圖4（a）中暫態工作點處電壓穩態值為（vsa，isa），在暫態工作點處對f（vsa）、f（iL）分別添加小信號動態擾動值Δvsa、ΔiL，然后按泰勒級數的一階線性展開，得其中，γAPR表示函數f（iL）在電感電流值為iL時的微分值。

將式（6）代入式（5），得到其在暫態工作點處小信號線性狀態空間表達式：

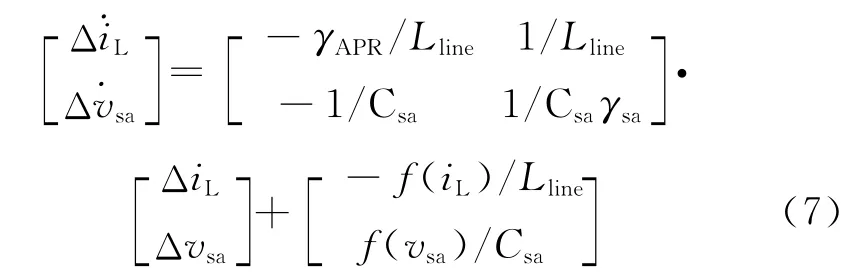
計算式（7）的特征根為

必須根據圖4（a）中暫態工作點在太陽電池陣輸出特性曲線的位置來判斷系統的穩定性：

1）最大功率點左側的電流源區段：γsa＜0，γAPR＜0并且∣γsa∣＜∣γAPR∣

在本區段范圍內，無論γsa，γAPR，Csa，Lline的數值如何，λ1或λ2中至少有一個特征根為正數，即至少有一個特征根位于s平面右側。根據李亞普諾夫穩定性定理可知，系統是不穩定的。

2）最大功率點右側的電壓源區段：γsa＜0，γAPR＜0并且∣γsa∣＞∣γAPR∣

在本區段范圍內，當γsa·γAPR＜Lline／Csa時，λ1和λ2均為負數，根據李亞普諾夫穩定性定理可知，系統是穩定的；當γsa·γAPR＞Lline／Csa時，λ1和λ2均為正數，系統是不穩定的。

因此，在MPPT 不調節母線電源系統設計上，必須滿足“γsa·γAPR＜Lline／Csa”的條件，才能保證電源系統在充電及電壓控制域下的穩定性。

4 結論

本文提出一種MPPT 不調節母線電源系統拓撲結構，針對其兩域控制模式，分別建立了太陽電池陣源端與負載端穩態分析的等效電路模型，采用小信號等效分析方法，對系統穩定性進行分析。

通過研究，得到以下結論：①無論源端與負載端特性曲線及電路參數如何設置，在MPPT 控制域內，電源系統始終保持穩定；②在充電及電壓控制域內，電源系統的穩定與否是有條件限制的，即必須保證源端／負載端特性曲線及電路參數滿足“γsa·γAPR＜Lline／Csa”的條件，才能保證電源系統穩定。

（References）

［1］劉治鋼，蔡曉東，陳琦．采用MPPT 技術的國外深空探測器電源系統綜述［J］．航天器工程，2011，20（5）：105-110

Liu Zhigang，Cai Xiaodong，Chen Qi．Overview of electrical power system design based on MPPT for deep space spacecraft［J］．Spacecraft Engineering，2011，20（5）：105-110（in Chinese）

［2］ESA．MPPC Regulated bus power system management for LEO and GEO missions［C］／／Proceedings of the 8th European Space Power Conference．Paris：ESA，2008：1-11

［3］Loche D．Mars Express and Venus Express power subsystem in-flight behaviour［C］／／Proceedings of the 8thEuropean Space Power Conference．Paris：ESA，2008：1-7

［4］Fiebrich H，Haines J，Tonicello F．Power system design of the Rosetta spacecraft［C］／／Proceedings of the 2nd IECEC．Washington D．C．：AIAA，2004：1-7

［5］Dakermanji G，Person C，Jenkins J．The Messenger spacecraft power system design and early mission performance［C］／／Proceedings of the 7th European Space Power Conference．Paris：ESA，2005：1-8

［6］Maset E，Sanchis-Kilders E，Weinberg A H．Ion drive propulsion MPP power conditioning system without battery［C］／／Proceedings of the 8th European Space Power Conference．Paris：ESA，2008：239-247

［7］Usman L，Shakeel B．Stability study of spacecraft electrical power system with constant-power loads［C］／／Proceedings of the 14th International Multitopic Conference．New York：IEEE，2011：217-221

［8］Luciano C，Paolo D，Alberto L．Maximum power point tracker point controller for unregulated bus architecture［C］／／Proceedings of the 7th European Space Power Conference．Paris：ESA，2005：1-6

［9］蔡曉東，劉治鋼，張明，等．混合式MPPT 星載電源系統拓撲設計與仿真分析［J］，航天器工程，2013，22（3）：77-82

Cai Xiaodong，Liu Zhigang，Zhang Ming，et a1．Design and simulation of a mixed MPPT electrical power system topology［J］．Spacecraft Engineering，2013，22（3）：77-82（in Chinese）

［10］王宇賓，常鮮戎，羅艷，等．基于隱式Taylor級數法的電力系統暫態穩定計算［J］．華北電力大學學報，2005，32（2）：1-6

Wang Yubin，Chang Xianrong，Luo Yan，et al．An implicit Taylor series method for simulation of power system transient［J］．Journal of North China Electric Power University，2005，32（2）：1-6（in Chinese）

［11］奚國華，沈紅平，喻壽益，等．基于全階狀態觀測器的無速度傳感器DTC系統［J］．電氣傳動，2008，38（7）：22-25

Xi Guohuang，Shen Hongping，Yu Shouyi，et al．Speed sensorless DTC system based on full-order state observer［J］．Electric Drive，2008，38（7）：22-25 （in Chinese）