水平荷載下框架—剪力墻受力性能分析

■張繼仁 ■萍鄉市規劃勘察設計院，江西 萍鄉 337000

框架能夠形成靈活自由的使用空間以滿足不同的建筑功能要求，而剪力墻能提供較高的抵抗側力的強度和剛度，能承受由強烈地震所產生的水平荷載，因此框架—剪力墻結構體系在辦公樓、旅館等公共高層建筑中得到了廣泛的應用。當框架—剪力墻結構體系承受水平荷載時，框架與剪力墻通過樓板的協同工作，因此二者的變形必須相互協調。

為了保證框架與剪力墻能夠共同承受側向力，樓蓋結構在其自身平面內的剛度必須得到保證。一般在進行框架—剪力墻結構內力與位移計算時，都假設樓板剛度在自身平面充分大。然而，由于建筑與結構上的需要，樓板由于開洞口而往往不能滿足上述假定，因此需要考慮樓板的變形。本文從兩方面的出發，通過解析解的形式將綜合剪力墻的頂點集中力解出來，以決定是否考慮這個力對結構體系的影響。連梁作為框架—剪力墻主要受力構件之一，對于其是否剛接歷來只是在概念設計的層面上，本文在這方面也做一定的工作。

1 不考慮樓板的變形

1.1 框架—剪力墻的計算基本假定

在對框架—剪力墻進行結構計算簡圖的確定時，作出如下的假定:

(1)樓蓋在自身平面內的剛度為無窮大;

(2)水平外荷載的合力通過結構的抗側剛度中心;

(3)框架與剪力墻的結構剛度系數沿結構的高度方向為常數。

通過這樣的假定，得到在同一標高的地方，結構的側移是相同的，這樣就可以把所有的框架與剪力墻等效為綜合的框架與綜合的剪力墻，從而把空間問題轉換到平面問題。根據連梁的約束能力的強弱，框架—剪力墻結構體系有下列兩種情況(如圖1所示):

圖1 框架—剪力墻結構體系

a)鉸接連梁;b)剛接連梁。

1.2 框架—剪力墻變形特點

在水平荷載作用下，單獨的框架的側向位移曲線呈剪切型(圖2(a))，而單獨的剪力墻的側向位移曲線呈彎曲型(圖2(b))。在框架—剪力墻結構體系中，框架的底部層間側移大，而剪力墻相對較小，剪力墻對框架的變形有“制約”的作用，而在結構的頂部，剪力墻的層間側移大，框架的相對較小，因此框架對剪力墻的變形有“扶持”的作用。剪力墻與框架在樓蓋協調下相互作用(借助于樓蓋結構平面內的剪力實現)，形成的側向位移曲線為彎剪型(圖2(c))，相互的作用機理如圖2(d)示。

在圖2(d)中，很明顯可以看到在框架與剪力墻的頂部作用著一對方向相反、大小相等的集中力，在眾多的文獻中，都認識到了這個荷載，并且提示在設計的時候要注意這個荷載，以保證頂層剪力墻與框架的整體性。關于這對相互作用力的大小，并沒有一個量化的值，因此也就很難客觀的評定這對作用力對結構的影響程度如何。

圖2 框架與剪力墻的相互作用示意圖

1.3 框架—剪力墻頂點集中力計算分析

當前，常用的框架—剪力墻結構體系所承受的水平荷載一般認為分為均布荷載、頂點集中荷載、倒三角形分布荷載三種。本文先從均布荷載出發，詳細推導計算框架—剪力墻結構體系框架與剪力墻頂部的作用力的詳細過程，其余的兩種荷載形式由于推導的過程相似，因此只是給出結果，并不給出計算過程。在水平均布荷載作用下，框架—剪力墻剛接連梁體系的剪力墻受到頂點集中力、剪力墻承擔的外荷載以及連梁的約束彎矩三種荷載作用(見圖1(c))，頂點集中力的計算過程如下:

(1)框架—剪力墻結構體系的綜合剪力墻任意高度的截面名義剪力為［1］:

其中:

其中:p-均布外荷載，H-建筑總高，x-結構的任意高度;

Cf-綜合框架抗推剛度，Cb-綜合連梁的等效剪切剛度;

η-連梁剛度折減系數，當設防烈度為6度時不宜小于0.7，7、8、9度的時不宜小于0.5，計算風荷載作用下的內力與位移時，取為0。

(2)框架—剪力墻結構體系的綜合剪力墻任意高度的截面剪力為［3］:

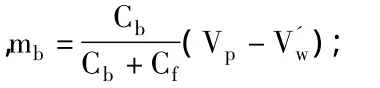
Vp-外荷載p在任意高度產生的剪力值。

其中Fp、Fq、FF分別表示在均布荷載p、倒三角形荷載q、頂點集中荷載F水平作用下的頂點集中力值。

1.4 實例分析

某10層框架—剪力墻結構，層高除底層為4m外均為3m，連梁與墻剛接，剪力墻厚度為0.3m，連梁截面尺寸分別取250mm×1000mm，250mm×400mm，250mm×250mm，框架柱截面尺寸為500mm×600mm，梁截面尺寸為250mm×600mm，混凝土強度等級為C30，結構尺寸及所受荷載如圖3所示。

圖3 框架—剪力墻結構示意圖

(1)各參數的值見表1所示;

表1 框架—剪力墻各參數值

(2)當連梁一端剛接一端鉸接時，計算出來的綜合剪力墻頂點集中荷載見下表2。

表2 不同荷載形式作用下的F值

(3)當連梁兩端均是鉸接的時候，計算出來的綜合剪力墻頂點集中荷載見下表3。

表3 不同荷載形式作用下的F值

(4)連梁剛接在頂點處對綜合剪力墻產生的約束彎矩見表4。

表4 不同荷載形式作用下的連梁約束彎矩值

(5)不同荷載形式綜合剪力墻的頂層底面彎矩值見表5。

表5 不同荷載形式作用下的綜合剪力墻彎矩值

2 考慮樓板的變形

一般情況下，高層建筑結構內力與位移分析采用樓板剛性假定是可以的。但是，在一些情況下則有必要考慮樓板變形產生的影響，尤其是抗側力結構剛度沿豎向有突變(如框支剪力墻結構)、樓板剛度較小、主要抗側力結構間距大以及層數較少時，樓板變形影響較顯著，不能將樓板面內剛度視為無限大。

基于此，文獻［2］、［3］考慮樓板的變形，通過將桿件沿高度方向連續化建立微分方程，并借助常微分求解器求出側移后，再得出各榀抗側力構件的內力，并與樓板剛性假定得到的數據進行對比分析，其中結構頂部(30m)的剪力見表6。通過本文表達式(1)、(2)、(3)進行計算，在考慮樓板變形的情況下可以算出綜合剪力墻頂點集中力為零。

表6 剪力墻和框架頂部(30m處)剪力

3 結語與建議

(1)由表2及表3知道，無論是連梁剛接還是鉸接，當不考慮樓板的變形時，對于各種水平荷載的作用，框架——剪力墻結構頂點處存在集中力，且不為零。由表6可以看出，考慮樓板變形時，該項集中力為零。

(2)由表2可以看出，三種水平荷載作用下，剛度特征值為2.42時，頂部集中力最小，且集中荷載作用下，頂部集中力與結構底部總剪力的比值在22%～36%之間;倒三角形荷載作用下，頂部集中力與結構底部總剪力比值在9% ～17%之間;均布荷載作用下，頂部集中力占結構底部總剪力的比值在6%～11%之間。

(3)由表3可以看出，隨著剛度特征值的增大，頂部集中力增大，且集中荷載作用下，頂部集中力不低于結構底部總剪力的50%;倒三角形荷載作用下，頂部集中力與結構底部總剪力比值在25%～40%之間;均布荷載作用下，頂部集中力占結構底部總剪力的比值在15% ～25%之間。

(4)由表4、表5可以看出，當λ=1.61(連梁截面尺寸為250mm×250mm)時，連梁端部的約束彎矩與頂層綜合剪力墻的底部彎矩之比分別為:集中力16.9%，均布荷載13.6%，倒三角形荷載15.4%，均比λ=2.42、4.00時的情況占比要小。

(5)文獻［4］認為結構的剛度特征值的范圍介于［1.15，2.4］之間能使框架和剪力墻充分發揮作用。由此看出，連梁截面尺寸250mm×250mm對應的連梁符合度較好。此外，連梁截面250mm×250mm的情形，比較符合根據跨高比估算梁截面尺寸的情形，即一般按(1/12-1/8)l(l為梁跨度)估算梁的截面高度。因此，按照這樣的方法估算截面的梁，建議按照鉸接來處理。

［1］彭偉.高層建筑結構設計原理(M).成都:西南交通大學出版社，2004，288 ～304.

［2］包世華，袁駟.高層建筑結構考慮樓板變形時的連續化常微分方程求解器解法［J］.建筑結構學報，1995，(4):16-20.

［3］陳伯望，沈蒲生.非剛性樓板對高層建筑結構內力和位移的影響分析［J］.四川建筑科學研究，2004，30(4):23～25.

［4］譚文輝，李達.高層建筑結構設計(M).北京:冶金工業出版社，2011，220-225.