一種改進的人工魚群聚類算法

李小培，張洪偉，鄒書蓉

(成都信息工程學院計算機學院，四川成都610225)

0 引言

數據挖掘中的聚類是將數據樣本按照最近鄰原則劃分到不同的類簇中，并達到相同簇中數據對象相似度最大，不同簇中數據對象相似度最小的目的[1]。由此，可以迅速發現數據對象之間的種種關系，從而方便研究和處理。雖然聚類分析算法因為待聚類的數據樣本的屬性類型和聚類目的而有差異，但是通?？蓺w結為以下幾類[2]:基于網格的方法、基于密度的方法、劃分方法、層次方法、基于智能的方法等[3－7]。傳統的聚類算法雖然各有所長，都能處理適合自身算法的特定問題，不可否認的是仍然有許多不足之處。比如說對數據樣本中的噪聲數據和孤立點處理能力較弱，隨著數據樣本集的不斷增長導致算法執行效率降低，樣本集的輸入次序影響聚類結果等。隨著社會不斷進步，智能技術快速發展，它能夠處理高維高復雜性數據、對初始樣本集不敏感、收斂速度快且正確率高，越來越多的人嘗試著用智能算法解決聚類問題[8]。

李曉磊[9]2002年首次提出基于智能思想的人工魚群算法。算法的基本思想是:一片水域中食物濃度最高的地方也是魚類生存數目最多的地方。根據這一特點構造人工魚的4種基本行為:隨機行為、覓食行為、聚群行為和追尾行為。通過人工魚的個體尋優達到凸顯整個魚群最優解的目的。該算法的主要特點有對初始值的設定不敏感、能夠處理高維高復雜性問題、尋找最優解的速度快等。人工魚群算法已經在神經網絡、聚類分析、圖像分割等領域得到廣泛的應用[10－12]。

1 K-Means聚類算法

假設在N維數據空間中，樣本集X有n個數據樣本xi={xi1，xi2，…，xiN}，i=1，2，…，n，也就是說每個數據樣本都有N個屬性值。這n個數據樣本構成數據的樣本集是一個n×N矩陣。根據每個樣本都應被分配到離自身最近的類簇中這一原則，將樣本集中的數據記錄劃分到P個互不相交的子集中。每個子集Ck={xki|xki?X}，其中xki表示被劃分到第k=1，2，…，P個子集中的數據樣本。這P個子集互不相交，而且它們的補集是整個數據集，其數學模型如下:

K-Means是聚類算法中的經典[13－14]，主要步驟:

(1)在樣本集{x1，x2，…，xn}中隨機選擇K個樣本記錄，作為K個類簇中心。

(2)計算出樣本xi，i=1，2，…，n到各個類簇的距離，并將樣本xi劃分到距離自己最近的類簇中，即如果‖xi-cj‖＜ ‖xi-cl‖ ，j=1，2，…，K ，l=1，2，…，K 且 l≠ j。那么就將樣本 xi劃分到 cj中。

(3)根據各個類簇中所含的樣本及樣本數目，重新計算K個類簇的中心，令c'i=ci。

(4)計算各個類內誤差之和。

(5)如果各個類簇中心不再變化或算法達到一定的迭代次數，還可以是e＜ε，ε是一個很小的正數，則算法停止。

2 人工魚群算法

假設有n條數據記錄，每條數據記錄有N個屬性，將這些數據記錄聚成K個簇。共有T條人工魚，人工魚的視野、擁擠度因子、步長、覓食行為的最大嘗試次數、人工魚算法的最大迭代次數分別用 visual、delta、step、try－number、MaxGen表示。人工魚的隨機、覓食、聚群、追尾行為的描述如下。

(1)隨機行為:隨機行為是4種行為中最簡單的一種行為，不一定能夠移動到最優解，但是它能夠解決陷入局部極值的困難。

(2)覓食行為:人工魚Xi在visual鄰域內尋找較優的位置Xj，如果Xj的目標函數值小于Xi，那么人工魚就向Xj移動，否則繼續尋找。如果在try－number次沒有找到，則人工魚執行隨機行為。

(3)聚群行為:人工魚Xi在visual鄰域內尋找自己的伙伴并統計伙伴的數目nf。如果nf=0，人工魚就執行覓食行為，否則計算出人工魚的聚類中心Xj。計算Xj的目標函數值Yj。如果滿足條件，那么Xi就向Xj移動，否則執行覓食行為。

(4)追尾行為:人工魚Xi在視野范圍內尋找伙伴并記下伙伴數據nf。找出目標函數值最小的伙伴Xj，并計算出Xj對應的Yj。如果，那么人工魚就向Xj移動，否則執行覓食行為。

3 改進的人工魚群聚類算法

文中算法的基本思想:在N維空間中，將n個數據記錄分成K類，每條人工魚就代表一個類簇中心，它是一個K×N的矩陣。首先對每條人工魚進行初始化。然后讓每條人工魚選擇追尾、聚群、覓食、隨機行為中的一種執行，執行完相應操作后利用K-Means算法進行優化并計算出人工魚的食物濃度，不斷重復人工魚的位置更新和K-Means算法優化操作，直到算法結束。

3.1 改進的人工魚群聚類算法中的元素說明

(1)決策變量:每條人工魚個體就是一個決策變量，同時也代表K個類簇中心。故人工魚的位置向量Xi=(ci1，ci2，…，ciK)，ci，i=1，2，…K表示第i個聚類中心，是一個N(每條數據記錄的屬性個數)維的矢量。即每條人工魚都是一個K×N的矩陣。

(2)目標函數:按照最近鄰原則將數據樣本劃分到某條人工魚個體的相應類簇中，并計算出各個數據樣本與最近類簇中心的方差和，這就是該條人工魚的目標函數值，即目標函數值的計算公式，其中mk是第k個類簇中樣本的個數，xki代表屬于第k個類簇的樣本，cjk表示第j條人工魚的第k個類簇中心。

(3)兩條人工魚之間的距離:計算兩條人工魚之間距離時采用歐氏距離進行計算。人工魚Xi=(ci1，ci2，…，ciK)，人工魚Xj=(cj1，cj2，…，cjK)之間的距離計算公式為

(4)人工魚的r鄰域:在人工魚群集合T中，某條人工魚Xi的鄰域指的是與該條人工魚的距離小于r的其他人工魚的集合，表示為 N(Xi，r)={Xj|distance(Xi，Xj)＜ r，Xj∈ T}。

(5)人工魚的聚類中心:假設人工魚Xi的鄰域內有nf條人工魚，這nf條人工魚都稱為人工魚Xi的伙伴，Xi的伙伴中心可表示為

3.2 人工魚群算法的改進

為了加快人工魚群算法的求解速度并且改善人工魚群算法的聚類精度，對人工魚群算法做如下改進。

(1)人工魚群算法使用動態移動步長。當人工魚的下一個位置的函數值比當前位置函數值小時，應該讓人工魚移動步長變大，讓人工魚移動(1+Yi－Yj)×step，其中Yi是人工魚當前位置的函數值，Yj是人工魚下一個位置的函數值?？梢约涌烊斯~找到最優解。

(2)為了讓人工魚更快地發現最優解，在覓食、聚群、追尾3種行為中加入全局最優人工魚的信息，即人工魚移動時將向全局最優人工魚和visual鄰域內最優人工魚的位置移動。這不僅加快求解速度也提高求解精度。

3.3 文中算法步驟

使用改進的人工魚群算法和K-Means算法進行結合。不僅克服了K-Means算法對初始類簇中心敏感的缺陷也改善了人工魚群算法容易陷入局部極值、后期收斂速度慢的弱點。兩者結合求解聚類問題的具體步驟如下。

(1)初始化算法中的相關參數，包括人工魚的規模(T)、視野(visual)、擁擠度因子(delta)、移動步長(step)、覓食行為最大嘗試次數(try－number)、文中算法最大迭代次數(MaxGen)類簇個數(K)、樣本個數(n)，樣本屬性個數(M)。

(2)初始化人工魚種群。人工魚的初始類簇中心采用隨機將樣本劃分到某個簇中，然后計算各個簇的樣本平均值并將其作為該簇的中心，得到的K個簇作為一條人工魚，不斷重復以上過程直到產生T條人工魚為止。

(3)根據目標函數計算公式求出每條人工魚的函數值，并記錄函數值最小的人工魚信息。

(4)人工魚嘗試執行聚群行為和追尾行為，如果聚群行為的目標函數值小于追尾行為，人工魚執行聚群行為，否則人工魚執行追尾行為。

(5)執行完相應行為后，用K-Means算法進行優化，并計算人工魚的目標函數值。

(6)如果人工魚的目標函數值小于全局最優人工魚的目標函數值，則更新全局最優人工魚信息。

(7)判斷是否每條人工魚都已經循環完畢，如果不是，則轉到步驟(3)。

(8)判斷是否達達到算法的最大迭代次數，如果否，轉到步驟(3)，如果是，算法結束。

4 仿真實驗

UCI機器學習數據庫是加州大學歐文分校提出，是一個常用的標準測試數據庫。所用實驗數據為UCI數據庫中的iris和glass兩個經典數據集。Glass數據集共有214條數據記錄，6個類標簽，每個數據記錄有9個屬性;iris數據集含有150條數據記錄，3個類標簽，每條數據記錄有4個屬性。

實驗所用的運行環境為，處理器:P22.99GHz;內存大小1.97GB，操作系統Windows XP，使用Java編程語言，Eclipse-SDK-4.2.2 運行平臺。

使用iris數據集做實驗時，文中算法設置的相關參數如下:人工魚群規模T=30，類簇個數K=3，人工魚視野visual=5，擁擠度因子delta=15，移動步長1，最大嘗試次數try－number=5，最大迭代次數MaxGen=100，KMeans算法的最大迭代次數為200。

使用glass數據集做實驗室，人工魚群規模T、最大嘗試次數 try－number、算法最大迭代次數 MaxGen、K-Means算法的最大迭代次數、擁擠度因子delta的設置同上，其他參數的設置如下:類簇個數K=6，人工魚視野visual=25。2個實驗程序分別獨立運行30次。

考慮到把30次的結果全部羅列出來篇幅太長，故選取其中的10次運算結果羅列出來如表1所示。同時還并將K-Means算法和文中算法的聚類性能進行比較，如表2所示。

表1 K-Means和本文算法對iris和glass數據集的10次運算結果

表2 K-Means算法和文中算法的聚類性能比較

從表1可以看出，文中算法能夠很好的改善聚類結果，如第1、4、5次僅用K-Means進行聚類，得到的類內間距為152.369、152.369、142.859，而將人工魚群算法和K-Means算法進行結合后計算的類內間距分別為78.941、78.941、78.941，類內間距分別減小48.2%、48.2%、44.7%。用數據維數較少的 iris數據集進行實驗時，K-Means算法計算的結果比較接近最優解，如2、3、6、7、8、9、10次計算的結果與最優解僅僅相差0.004。但是當數據維數增多，數據記錄數也增多時，K-Means最優解的誤差也相差較大。如對于glass數據集而言，10運行得到的誤差從小到大依次為:42.837、44.951、45.23、46.41、52.134、64.229、204.276、224.058、225.291、258.774。從表1中還可以看出，對于同一個數據集，追尾行為、聚群行為、覓食行為、隨機行為執行次數變化很小，這為最優解的穩定性奠定基礎。

從表2可以看出，不論是對Iris數據集進行測試還是對glass數據集進行測試，文中算法在30次的獨立測試中每次都能達到最優解。而K-Means算法沒有一次能夠收斂到全局最優解。

為了進一步測試文中提出的改進的人工魚群聚類算法的性能，文中算法和改進的遺傳聚類算法[15]、遺傳指導算法(GGA)、人工免疫C－均值聚類算法就程序獨立運行30次花費的時間(s)、最優值、平均值、平均值和最最優值的標準差Javr進行比較。比較結果如表3所示。其中改進的遺傳聚類算法參數設置如下:交叉概率Pc=0.9，變異概率Pm=0.005，種群大小Psize=30。GGA和人工免疫C-均值聚類算法的結果在文獻[13]中已給出。

表3 K-Means算法和文中算法的聚類性能比較

表3的結果可以說明，對于iris數據集，改進遺傳聚類算法和文中算法都取得了最優解，收斂速度和精度都要由于遺傳指導算法和人工免疫C-均值聚類算法。但是文中算法的收斂速度比改進的遺傳聚類算法還要快。對于glass數據集，文中算法不僅最優值優于GGA和人工免疫C-均值聚類，而且算法運算時間遠遠小于二者。雖然改進的遺傳算法也達到了最優值，但是并不是程序每次運行都能達到最優值，而文中算法卻可以每次都能達到最優解，且運行時間短。

圖1和圖2是用文中算法對Iris數據集合wine數據集進行聚類時，目標函數值與進化代數之間的關系。從圖中可以看出本文算法收斂速度非?？臁?/p>

圖1 iris數據集的函數值隨迭代次數變化過程

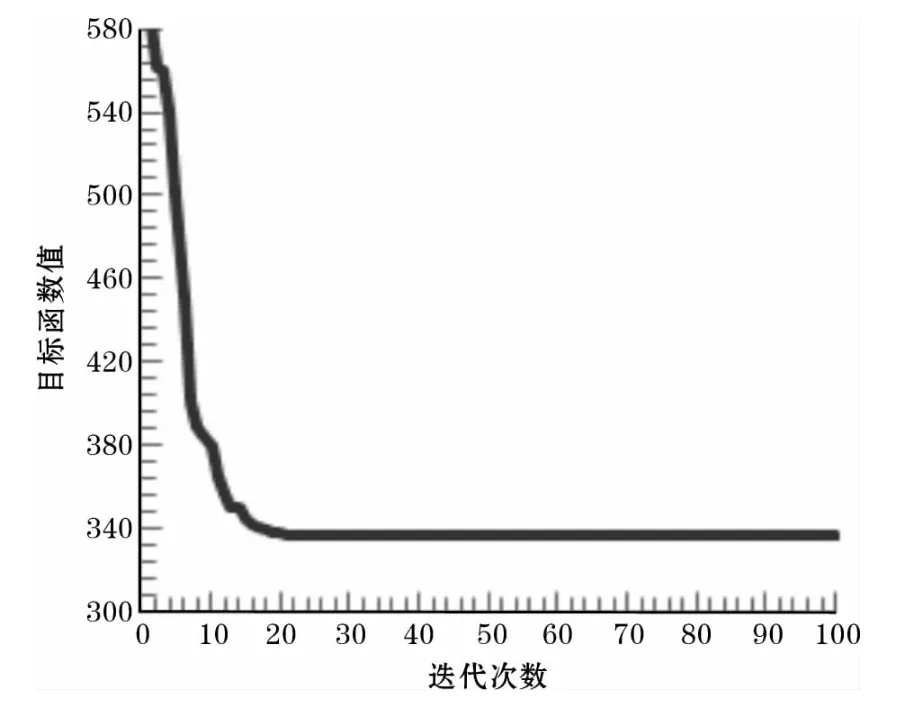
圖2 glass數據集的函數值隨迭代次數變化過程

4 結束語

提出的改進的人工魚群聚類算法，是在聚類數目已知的前提下，對數據樣本進行聚類。作為經典劃分聚類算法的K-Means雖然具有簡單、易實現等優點，但是也存在諸多缺點，如對初始值的選取提交敏感、聚類精度不高等。人工魚群算法是一種新型的仿生智能優化算法，可以很好的解決K-Means算法遇到的問題，兩者結合起來可以做到揚長補短。為了加快聚類的速度并改進聚類的精度，對人工魚群的視野、移動步長、覓食、聚群、追尾行為進行改進，并與K-Means算法進行融合。實驗使用了UCI機器學習數據庫中的經典數據集，通過表1－3以及圖1－2可以看出文中算法求解結果穩定，聚類效果較好。雖然文中算法聚類性能較高，但是仍然需要做進一步的研究，如確定算法中相關參數對聚類結果的影響，進一步提高聚類的收斂精度和速度等。

[1] 周濤，陸惠玲.數據挖掘中聚類算法研究進展[J].計算機工程與應用，2012，48(12):100－108.

[2] 李秀芳，李志成.基于數據挖掘的聚類算法研究[J].計算技術與自動化，2006，25(3):41－44.

[3] Huang Jianghua，Zhang，Junying.Distributed Dual ClusterAlgorithm Based on Grid for Sensor Streams[J].International Journal of Digital Content Technology and its Applications.2010，4(9).

[4] Yu Yongqian，Zhao Xiangguo，Chen Hengyue，et al.Self-expanded clustering algorithm based on density units with evaluation feedback section[J].Wuhan University Journal of Natural Sciences，2006，11(5).

[5] Xiaoyun Fan，Baoshan Cui，Kejiang Zhang，et al.Water Quality Management Based on Division of Dry and Wet Seasons in Pearl River Delta[J].Clean Soil Air Water，2012，40(4).

[6] 陳旭玲，樓佩煌.改進層次聚類算法在文獻分析中的應用[J].數值計算與計算應用，2009，11(4):277－281.

[7] 熊勰，劉光遠，溫萬惠.基于智能算法的生理信號情感識別[J].計算機科學，2011，38(3):266－268.

[8] 呂謀，董深，韓偉，等.基于智能算法的多水源泵站在線優化控制技術[J].系統工程理論與實踐，2010，30(1):140－144.

[9] 李曉磊，邵之江，錢積新.一種基于動物自治體的尋優模式:魚群算法[J].系統工程理論與實踐，2002，22(11):32－38.

[10] Wang C R，Zhou C L，Ma J W.An Improved Aritificial Fish-swarm Algorithm and its Application in Feed-forward Neural Networks[J].Proceedings of the Fourth International Conference on Machine Learning and Cybernetics，2005:2890－2894.

[11] 蘇錦旗，吳慧欣，薛惠鋒.基于人工魚群算法的聚類挖掘[J].計算機仿真，2009，2(26):147－150.

[12] 丁生榮，馬苗，郭敏.人工魚群算法在自適應圖像增強中的應用[J].計算機工程與應用，2012，48(2):185－187.

[13] 張琳，陳燕，汲業，等.一種基于密度的K-means算法研究[J].計算機應用研究，2011，28(11):4071－4085.

[14] 陳光平，王文鵬，黃俊.一種改進初始聚類中心選擇的K-means算法[J].小型微型計算機系統，2012，6(6):1320－1322.

[15] 陸林花，王波.一種改進的遺傳聚類算法[J].計算機工程與應用，2007，43(21):170－172.