先驗信息可信度在成敗型試驗中的應用

趙 勇，劉建新，牛青坡

（中國空空導彈研究院 河南 洛陽 471000）

在武器研制各階段的試驗中，幾乎所有的產品試驗中都能收集到成敗型數據[1]，如引信作用可靠性試驗中引信的啟動成功與失敗。鑒于時間和成本的考慮，如何在一定試驗量的情況下正確評估武器的性能是人們在武器性能鑒定中急需解決的難題。為此提出了應用Bayes評估的小子樣理論，Bayes小子樣試驗鑒定方法[2]。Bayes顯著特點是運用了多種驗前信息，特別是大量的仿真信息[3]。由于大量的驗前信息的應用，現場試驗信息就有被驗前信息“淹沒”的危險，從而削弱了現場試驗信息在武器系統評估中的地位，造成鑒定結果主要由驗前信息決定的現象。因此，在應用Bayes方法評估武器性能時，即使驗前信息和現場試驗信息通過了相容性檢驗，也不免讓人們對Bayes方法心生疑慮[4]。在成敗型試驗中，如果驗前信息本身就是主觀設定或者可信度不高，而在運用Bayes方法時又是將驗前信息和現場試驗信息簡單的混合使用，就必然會引起人們上述的擔心。所以科學的使用驗前信息和現場試驗信息就成為消除人們疑慮的關鍵。

1 可信度的概念

這里，我們利用統計檢驗法，在一致性檢驗的基礎上，給出嚴格的驗前信息可信度的概念。

記X=(X1, …Xn1)為仿真信息或歷史信息；Y=(Y1, …Yn2)為現場試驗信息。為了檢驗這兩種信息是否一致或是否屬于同一總體，引入競擇假設：

H0：X和Y屬于同一總體；

H1：X和Y不屬于同一總體。

若已知：當H0為真而拒絕H0的概率為α，即棄真的概率為α；而當H0為真而采納H0的概率為1- α。

為了引入驗前子樣（仿真子樣）的可信度，記

A:采納H0的事件；

根據上述內容可得：

定義：當采納了H0之下，H0成立的概率，即X和Y屬于同一總體的概率，稱為驗前子樣X的可信度。即可信度為P(H0|A) 。

2 可信度的計算

依據上述定義，利用Bayes公式可得

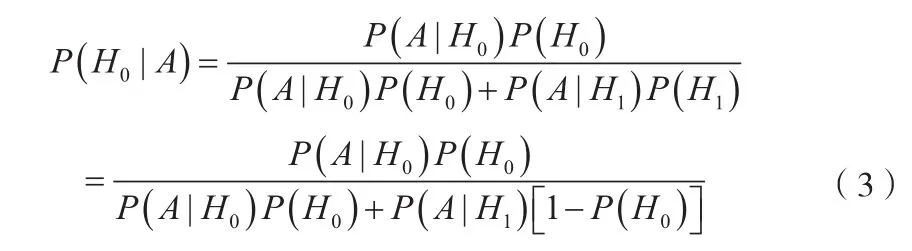
式中：

P(A|H1) =β為采偽概率，即當H1為真而采納了H0的概率。這樣驗前信息的可信度可表示為：

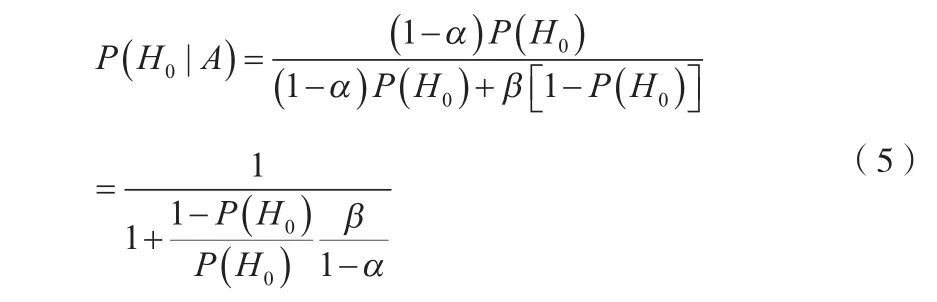
在應用中，X為驗前子樣，如仿真所獲得的子樣；Y為現場（真實）試驗所表示的子樣。因此所謂X的可信度就是以Y作為比較標準，X和Y吻合的程度。

由可信度的表達式，計算中必須給出P(H0)、α和β。其中P(H0)是驗前概率，α是棄真概率，β是采偽概率。上述參數必須在試驗之前計算出來，如果在試驗之前沒有任何信息可以利用，則可以取P(H0)=0.5。當然，這只是一種設想，必須十分慎重，例如X是仿真子樣，則經過仿真中的V.V&A處置，不能認為P(H0)=0.5，至少有 P(H0)＞0.5。

如果取 P(H0)=0.5，此時上式簡化為

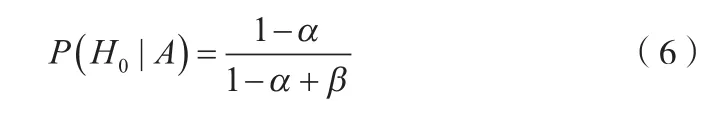
2.1 P(H0)的計算

驗前概率P(H0)指的是獲得現場信息之前，事件H0成立的概率，它的大小反映的實際上是獲取驗前信息的方法或過程的可信度[5]。這種可信度受驗前信息獲取時的試驗方法、試驗條件、試驗數據處理方法以及工程實踐經驗等多種因素的影響。下面通過引入信息似然比來確定P(H0)，假設由信息I1，可得到一個概率向量:

0111

由于H0和H1是對立假設，所以p1(H0)和p1(H1)滿足下列關系：

信息似然比與概率之間的相互確定關系為：

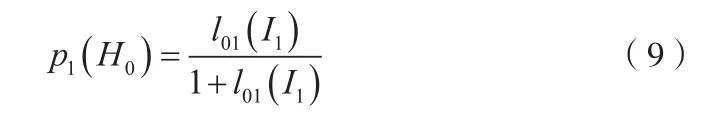
給出信息I1后，再給出信息I2的條件似然比用l01(I2/I1)表示：

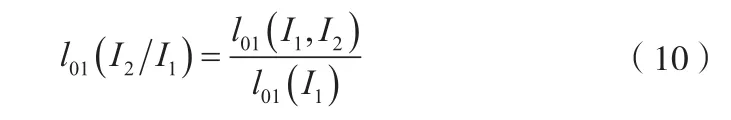
于是可以給出：

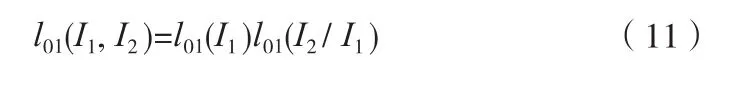
對于n種相互獨立的信息，可以導出：

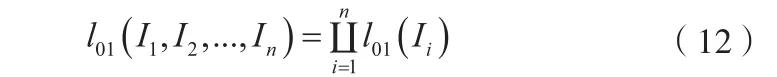
從一般意義上來說，由于各種信息來自于與之相對應的不同方面，所以在大多數情況下，不同來源的信息是相互獨立的。所以有n種信息的情況下，信息似然比與概率之間的相互確定關系為：

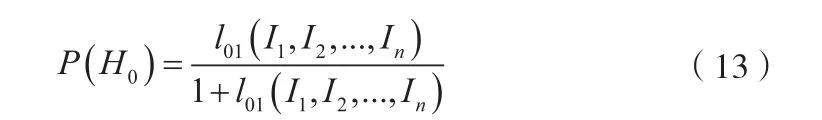
需要說明的是如果在實驗之前沒有驗前信息可以利用，則可以取P(H0)=0.5，當然這只是一種設想，必須十分慎重。例如，如果Z0是仿真子樣，則經過仿真中的V.V＆A處置，不能認為P(H0)=0.5，至少應有P(H0)＞ 0.5。

2.2 α和β的確定

由于α和β分別代表了生產方的風險（棄真）和使用方的風險（存偽），所以在進行檢驗方案設計時，應從工程實際情況來確定α和β。需要指出的是，要一般給出β的解析式是很困難的。對于有驗前信息可以利用的情況，可以利用上節2.1的方法來計算P(H0)。采用“風險上平等對待的原則”來計算α和β（工程上一般取1%—5%）。此時驗前子樣的可信度為：

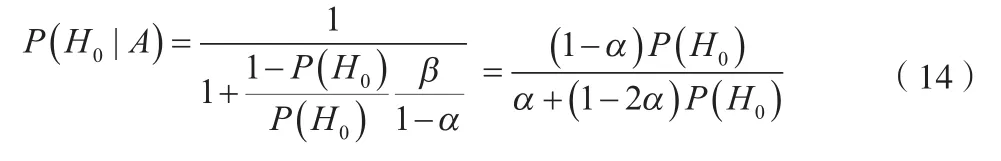
3 可信度在Bayes評估中的應用

在裝備試驗中，常常會遇到成敗型試驗產品，這種成敗型產品待檢參數服從二項分布。例如引信啟動的可靠度、導彈的命中概率[6]、雷達目標識別率等，本文以某型號導彈的飛行打靶試驗為例進行討論。設導彈命中率θ的先驗分布為Beta分布，即

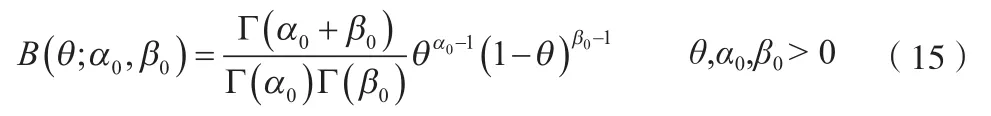
式中，α0,β0為分布參數，可由驗前信息計算。若在打靶試驗之前獲得驗前信息（仿真）經折合得到數據Z0=(m1,n1)，其中m1是經折合后打靶試驗命中次數，n1是經折合后打靶試驗次數。則

當進行現場打靶試驗得到數據Z1=(m2,n2)后，θ的后驗分布仍為貝塔分布。其中m2是現場打靶試驗命中次數，n2是現場打靶試驗次數。θ的后驗分布為：

式中分布參數α, β為

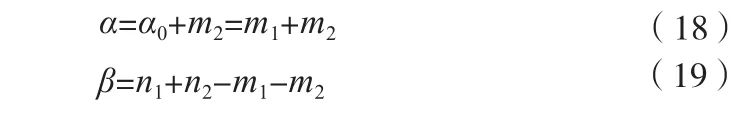
從而導彈命中率θ的Bayes估計為

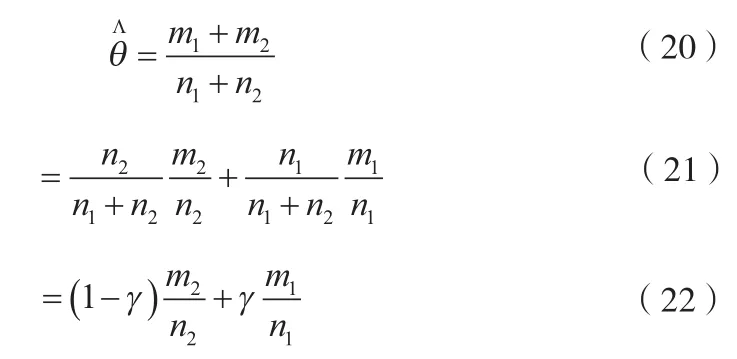
對于導彈命中概率的檢驗，構造如下統計假設：

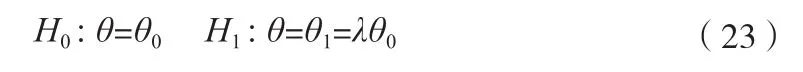
λ 為檢出比（0 ＜ λ ＜ 1 ）。

運用Bayes檢驗,如果決策不等式

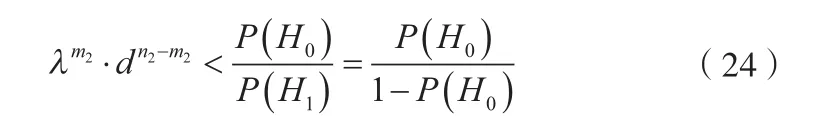
則采納H0；如果決策不等式

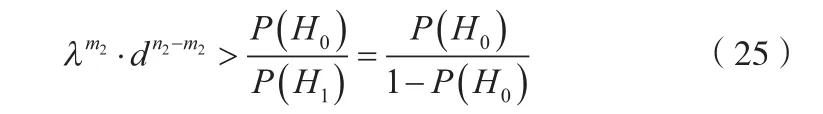
則采納H1。其中d為鑒別比，且滿足

P(H0)=P(H0|Z1)P(H0|A)為原假設H0的驗前概率，由驗前信息確定，且

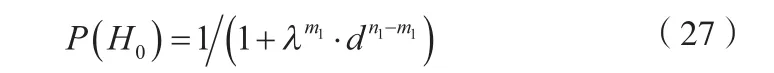
P(H1)為備擇假設H1的驗前概率。由于H0和H1是對立假設，所以

在上述Bayes估計中，如果不顧驗前信息可信度的大小，直接將驗前信息簡單的用于Bayes統計推斷中，在驗前信息量（仿真信息）巨大的情況下，必將造成“淹沒”現場數據的現象，此時的現場數據在幾乎起不到任何作用。

同樣在上述的Bayes假設檢驗中，如果不顧驗前信息可信度的大小，此時，如果驗前樣本巨大（遠超出現場樣本），則驗前信息將作出必然采納H0或H1的決策。若必然采納H1，即P(H0)=0。則式（24）的不等式必成立，即不管現場子樣如何取值，必將使采納H1的不等式成立。此時的現場信息不起任何作用，完全被大量的現場信息所“淹沒”。所以在使用驗前信息時必須考慮其可信度，于是真實的驗前概率P(H0)* ：

其中，P(H0)表示在獲得現場子樣Z1前假設H0成立的概率。P(H0|A)表示驗前子樣Z0的可信度。在應用中，所謂的驗前子樣Z0的可信度也就是以現場子樣Z1為標準，Z0和Z1的吻合程度。這樣即使驗前子樣的容量很大，提供的信息非常豐富，即

但由于此時真實的驗前概率為P(H0)* ：

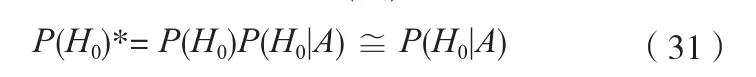
在計算中就不能將大量的驗前子樣與現場子樣直接簡單的混用。

故引入驗前信息可信度后不存在大量驗前子樣（如仿真信息）“淹沒”現場子樣的情況。不會再出現驗前信息在可信度不高的情況下決定試驗決策的情況；當然此時在做參數θ 的Bayes推斷統計時，同樣由于驗前子樣可信度的存在，不能將驗前子樣直接與現場子樣簡單的混合使用，必須將現場子樣重新折合后才能使用，這樣必將引起權系數γ的變化，就不會在大量驗前子樣可信度較低的情況下，驗前子樣決定參數θ 的Bayes推斷統計的結果。

4 結 論

事實上，在武器系統成敗型試驗中，使用Bayes方法評估產品性能的最關鍵問題是驗前信息的收集過程必須真實可靠，也就是說驗前信息在使用時其可信度P(H0|A)必須要高。從而才能保證在使用Bayes方法作統計推斷時其結果的正確性。

對于成敗型試驗的Bayes統計推斷，如果驗前概率高(此時驗前子樣可信度高，驗前子樣數據不需要經過折合直接使用，權系數γ較大)，則驗前信息對統計推斷的結果“貢獻”更大。對于Bayes假設檢驗，如果驗前概率高(即驗前信息有利于假設H0)，則檢驗方案容易接受假設H0，也即正確的利用了驗前信息，得到了更合理的評估結論。

[1] 游寧，馬寶華.成敗型可靠性數據點估計與區間估計關系研究[J].探測與控制學報,1999,21(1):3-4.YOU Ning, MA Bao-hua.The research on the relationship between point estimation and interval estimation for success or failure model reliability data[J]. Journal of Detection &Control,1999,21(1):3-4.

[2] 姚志軍,王國平,王廣偉.驗前信息可信度及其在Bayes評估中的應用[J].火力與指揮控制,2007,32(7):51-53.YAO Zhi-jun,WANG Guo-ping,WANG Guang-wei.Confidence level of prior information and its application in bayes method[J].Fire Control and Command Control,2007,32(7):51-53.

[3] 張金槐,張士峰.驗前大容量仿真信息“淹沒”現場小子樣試驗信息問題[J].飛行器測控學報.2003,22(3):1-5.ZHANG Jin-huai,ZHANG Shi-feng. Problem of large numbers of prior information obliterating the small numbers of test information[J].Journal of Spacecraft TT&C Technology.2003,22(3):1-5.

[4] 武小悅,劉琦.裝備試驗與評價[M]. 北京:國防工業出版社，2008.

[5] 張金槐,劉琦,馮靜.Bayes試驗分析方法[M].長沙:國防科技大學出版社,2007.

[6] 趙建華,王磊,李濤.海上目標雷達回波圖像識別系統[J].兵工自動化,2012,31(12):61-65.ZHAO Jian-hua, WANG Lei,LI Tao.Sea target rader echo image indentify syestem[J].Ordnance Industry Automation,2012,31(12):61-65.