傳感器布置對水輪機振動特征參數影響研究

李瑞瑩，李志華

（河海大學 能源與電氣學院，江蘇 南京 211100）

振動是反映水輪機健康狀況及運行安全的重要指標。隨著科學技術的進步，一方面水輪機容量、比速和調節的越來越頻繁，使得對水輪機振動及運行安全的要求愈來愈高；另一方面，隨著傳感器技術的發展，振動檢測與分析的水平也在不斷上升。因而采用好的振動檢測方法，提高故障診斷及處理水平，將振動控制在合格范圍內，對水輪機正常運行有十分重要的意義。

文中從數學建模及仿真的角度研究傳感器布置對水輪機振動特征參數的影響，在傳統三點檢測法的基礎上，同時建立二點和四點法的主軸旋轉數學模型，以掃描點處的相對誤差為特征參數進行研究。第一、二、三節分別分析了3種傳感器布置方法對特征參數的影響，通過對仿真結果的比較得到最佳的傳感器布置方法。

1 三點布置法傳感器位置對振動參數影響

1.1 三點法主軸旋轉數學模型的建立

傳統的旋轉誤差三點法檢測原理圖如圖1所示。

圖1 三點法檢測原理圖Fig. 1 Detection principle diagram of three-point method

圖中，A，B，C為三個非接觸式渦流傳感器。O點為這3個測點的理想旋轉中心，以O點建立直角XOY坐標系，同時設∠AOB=α，∠BOC=β。取主軸系統的瞬時旋轉軸中心O為極心作極坐標系，極角θ為逆時針方向, R(θ)為主軸旋轉誤差，在極坐標中它可以分解為Rx(θ)，Ry(θ)。r(θ)是極坐標下θ角對應的主軸半徑。這樣整個主軸的運動就可以用主軸瞬時旋轉中心在直角坐標系中的旋轉誤差和主軸本身在極坐標系中的轉動[1]來描繪。

參考三點法檢測原理，建立三點法主軸旋轉模型[2]圖如圖2所示。

圖2 三點法主軸旋轉數學模型Fig. 2 Spindle rotation mathematical model of three-point method

如圖，已知主軸標準圓方程為x2+y2=r2，圓上任意一點的直角坐標為(x,y)，極坐標為(ρ,θ)，經過傾斜角δ，圓心平移到(x0,y0)后，圖形上任意一點的直角坐標變為(x1,y1)，新的旋轉平移方程可推導如下：

1)逆時針傾斜角，圖形上任意一點的極坐標值由(ρ,θ)轉化為 (ρ,θ+δ)

3)將解帶入標準圓方程，變形為

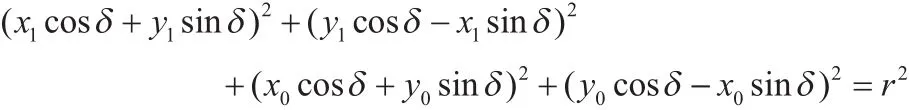
4)將三個傳感器與標準圓心所在直線看成三條掃描線，且設直線方程為y=kx，聯立該直線與上式可簡化為一個一元二次標準方程ax2+bx+c=0，其中

1.2 傳感器位置對振動參數影響

仿真時，設主軸旋轉的標準圓方程為x2+y2=402，以3個傳感器夾角α=120°，β=120°為標準情況來進行布置，此時掃描直線斜率k1=0，k2=-1.732 1，k3=1.732 1[3]。在MATLAB中仿真編程，可得到S1、S2、S3在相對掃描點處的測量數據(X1,Y1)、(X2,Y2)、(X3,Y3)。同時由于每個傳感器沿X和Y 方向的分量都有自己獨特的頻率成分，首先對測量數據進行FFT變換，將時域信號轉化為頻域信號[4]，進一步進行觀察。得到三點布置法中FFT波形圖如圖3所示。

對FFT波形圖進行分析，可知頻率對旋轉誤差幾乎沒影響，但振幅對旋轉誤差的影響卻很大，接下來只考慮振幅，忽略頻率對旋轉誤差的影響。

圖3 三點法FFT波形圖Fig. 3 FFT waveform of three-point method

當只α變化β不變時，以α=120°，β=120°為標準情況用“0”表示[5]；α每減小2°代表負偏離一個單位度，用“-1”表示；α每增加2°代表正偏離一個單位度，用“1”表示。由于α和β的變化只影響(X2,Y2)和(X3,Y3)的測量值，故以(X2,Y2)和(X3,Y3)為被測對象，同時以最大相對誤差值作為特征參數進行研究，經過MATLAB仿真，得到特征參數與角度的關系曲線如圖4所示。

圖4 三點法僅α變化時最大相對誤差曲線Fig. 4 Maximum relative error curve of three-point method only α change

觀察可知，隨α角度變化Y2和Y3最大相對誤差值幾乎沒什么影響，X2最大相對誤差隨α偏離度地增大明顯變小，X3最大相對誤差隨α偏離度增大明顯變大，總體而言，在-2～2的偏離范圍內，整體效果較好。

當只β變化α不變時，以α=120°，β=120°為標準情況用“0”表示；β每減小2°代表負偏離一個單位度，用“-1”表示；β每增加2°代表正偏離一個單位度，用“1”表示。由于β的變化只影響(X3,Y3)的測量值，故以(X3,Y3)為被測對象，同時以最大相對誤差為特征參數進行研究，經過MATLAB仿真，得到特征參數與角度的關系曲線如圖5所示。

觀察可知，隨β角度變化Y3最大相對誤差幾乎沒什么影響，但整體呈上升趨勢，在-10～0的偏離范圍內整體效果較好。

圖5 三點法僅β變化時最大相對誤差曲線Fig. 5 The maximum relative error curve of three-point method only βchange

2 二點布置法傳感器位置對振動參數影響

2.1 二點法主軸旋轉數學模型的建立

與三點法主軸旋轉數學模型類似，將傳感器個數減少為兩個，如圖6所示，便可得到兩點法主軸旋轉數學模型，S1,S1為兩個傳感器所在位置。二點法的數學模型分析過程與三點法類似，這里不再重復。

圖6 二點法主軸旋轉數學模型Fig. 6 Spindle rotation mathematical model of two-point method

2.2 傳感器位置對振動參數影響

仿真時，設主軸旋轉的標準圓方程為x2+y2=402，以傳感器夾角α=90°為標準情況來進行布置，此時掃描直線斜率k1=0，k2=1.6331e+016。在MATLAB中仿真編程，可得到S1、S2在相對掃描點處的測量數據(X1,Y1)、(X2,Y2)。

當α變化時，以α=90°為標準情況用“0”表示，α角度偏離度設置與三點法相同。由于α的變化只影響(X2,Y2)的測量值，而X2在標況下的真值為0，此時相對誤差無意義，故只將Y2的最大相對誤差作為特征參數進行研究，經過MATLAB仿真，得到特征參數與角度的關系曲線如圖7所示。

觀察圖7可知，隨α角度的變化Y2最大相對誤差在0.275%到0.325%范圍幅度變化較大，在1到10的偏離范圍內整體效果較好。

3 四點布置法傳感器位置對振動參數影響

3.1 四點法主軸旋轉數學模型的建立

與三點法主軸旋轉數學模型類似，將傳感器個數增加為4個，如圖8所示，便可得到四點法主軸旋轉數學模型，S1，S2，S3，S4為4個傳感器所在位置。四點法的數學模型分析過程與三點法類似，這里不再重復。

圖7 二點布置法Y2相對誤差曲線Fig. 7 Y2 relative error curve of two-point method

圖8 四點法主軸旋轉數學模型Fig. 8 Spindle rotation mathematical model of four-point method

3.2 傳感器位置對振動參數影響

仿真時，設主軸旋轉的標準圓方程為x2+y2=402，以傳感器夾角α=90°，β=90°，γ=90°為標準情況來進行布置， 此 時 掃 描 直 線 斜 率 k1=0，k2=1.6331e+016，k3=0，k4=1.6331e+016。在 MATLAB 中仿真編程，可得到S1，S2，S3，S4在相對掃描點處的測量數據(X1,Y1)、(X2,Y2)、(X3,Y3)、(X4,Y4)。

當只α變化，β、γ不變時，以α=90°，β=90°，γ=90°為標準情況用“0”表示；α角度偏離度設置與三點法相同。由于的α變化只影響(X2,Y2)、(X3,Y3)和(X4,Y4)的測量值，且在標況下，X2、Y3和X4的真值為0，此時相對誤差無意義，故只研究Y2、X3和Y4在變化時的相對誤差值，經過MATLAB仿真得到特征參數與角度的關系曲線如圖9。

由圖9可知，當α變化時Y2、X3和Y4三者的變化幅度都較大，Y2在偏離度為“1”時取得極小值，在-3～8的偏離范圍內效果較好；X3在“-9”處取得極小值，在-10～3的偏離范圍內效果較好；Y4在“6”處取得極小值，在0到7的偏離范圍內影響較小。總體而言，在0～3的偏離范圍內取得較好的效果。

當只β變化，α、γ不變時，只影響(X3,Y3)和(X4,Y4)的測量值，且在標況下，Y3和X4的真值為0，此時相對誤差無意義，故只研究X3和X4在β變化時的相對誤差值，經過MATLAB仿真，得到特征參數與角度的關系曲線如圖10所示。

分析圖10可知，隨變化，和的變化幅度在0.26%到0.32%的范圍內都較大。比較之下，在-2到7的偏離范圍內最大相對誤差較小；在-2到5的偏離范圍內受影響較小。總體而言，在-2到5的偏離范圍內效果較好。

圖9 四點法僅α變化時最大相對誤差曲線Fig. 9 Maximum relative error curve of four-point method only change α

圖10 四點法僅β變化時最大相對誤差曲線Fig. 10 Maximum relative error curve of four-point method only βchange

當只γ變化，α、β不變時，只影響到(X4,Y4)的測量值，又在標況下，X4的真值為0，此時相對誤差無意義，故只研究Y4在γ變化時的相對誤差值，經過MATLAB仿真，得到特征參數與角度的關系曲線如圖11所示。

圖11 四點法僅γ變化時最大相對誤差曲線Fig. 10 Maximum relative error curve of four-point method only change γ

由圖11可知，最大相對誤差值隨的變化在0.28%～0.32%的范圍內幅值變化大。在標況下取得最小值，且在-1～3的偏離范圍內整體效果較好。

3.3 仿真結果分析

將變化時3種傳感器布置的最大相對誤差曲線圖4、圖7和圖9進行比較，三點法中整體最大相對誤差在0.3%～1.4%的區域內變化，且最大值和最小值相差1%；二點法中最大相對誤差變化在0.275%～0.325%的區域內，最值之間相差0.05%；四點法中整體最大相對誤差在0.254%～0.324%的區域內變化，最大變化范圍是0.07%。從曲線變化幅度上看，二點法和四點法的穩定性要優于三點法，且在-7～2的偏離范圍內曲線整體效果較好。

同理，將β變化時不同布置方法的最大相對誤差曲線圖5、圖10進行比較，三點法中最大相對誤差變化在0.4%～1.4%的區域內，變化幅度為1%；四點法中整體最大相對誤差在0.26%～0.318%的區域內變化，變化范圍是0.047%。對比可知四點法在曲線變化幅度和最值方面都要優于三點法，且在-2～5的偏離范圍內曲線整體效果較好。將變化時的最大誤差曲線圖11進行分析，此時四點布置法在標況下取得最小值，且在-1～3的偏離范圍內整體效果較好。

4 結束語

文中以掃描點處的相對誤差值作為振動特征參數，從數學建模和仿真角度研究了傳感器布置對特征參數的影響。通過以上分析可知[6]，四點布置法的整體效果要優于二點法和三點法，且傳感器角度在-1～2的偏離范圍內，即α、β和γ布置在88°～94°的范圍內整體效果較好。

[1] 沙立華.水輪機發電機振動問題的處理[J].水電廠自動化,2008,29(3):1-2.SHA Li-hua.Turbine generator vibration problem handling [J].Hydropower Automation, 2008,29(3):1-2.

[2] 陳清,梁兵.主軸徑向回轉誤差測量中的誤差分析[J].湖南大學學報,2003,30(4):23-25.CHEN Qing,LING Bing. The spindle rotation error measurement of the error analysis[J]. Journal of Hunan University,2003,30(4):23-25.

[3] 張宇華，王曉琳.三點法中測頭最佳角位置的確定方法[J].光學精密工程,1998,6(5):39-45.ZHANG Yu-hua,WANG Xiao-lin.Three point method of measuring head best Angle position determination method[J].Optical Precision Engineering,1998,6(5):39-45.

[4] 洪邁生，鄧宏煌.加試和回轉運行誤差的時域二點法分離技術[J].中國機械工程,1997,8(2):88-92.HONG Mai-sheng,DENG Hong-huang.Add try tow point method of time domain and rotary operation error separation technique[J].Mechanical Engineering in China,1997,8(2):88-92.

[5] 范裕健，張社民，徐文雄.三測點法檢測的機理及數學模型[J].儀器儀表學報,1994,15(2):155-159.FAN Yu-jian, ZHANG She-min, XU Wen-xiong. Three points method to detect the mechanism and mathematical model[J].Journal of Instruments and Meters, 1994,15(2):155-159.

[6] 韋然.無線傳感器網絡節點的設計與實現[J].電子科技,2012(1):31-35.WEI Ran.Design and implementation of a general node for wireless sensor networks[J].Electronic Science and Technology,2012(1):31-35.