蟻群算法在求解TSP問題中的改進研究
王寶生,屈寶存
(遼寧石油化工大學 遼 寧 撫 順 1 13001)
旅行商問題(Traveling Salesman Problem,TSP)是一個易于描述卻難以處理的NP-HARD問題。近年來,它引起了許多學者的廣泛關注。旅行商問題不僅具有很重要的理論價值,而且還具有廣泛的實際應用價值,如機器人路徑規劃、電路板設計、城市管道鋪設優化、交通運輸以及物流配送等領域都可視為TSP問題的具體應用。對于旅行商問題,目前常用的方法有模擬退火算法、遺傳算法、神經網絡法等。
蟻群優化算法是模擬自然界中真實蟻群的覓食行為而形成的一種模擬進化算法。它是一種新興的仿生學優化算法,屬于元啟發算法的一種。它具有采用分布式并行計算機制、易于與其他方法結合、具有較強的魯棒性等優點,但其搜索時間長、易陷于局部最優解是其最突出的缺點。因此,既要使得蟻群算法的搜素空間盡可能的大,以尋找那些可能存在最優解的解空間,同時,又要充分利用螞蟻體內當前所有的有效信息,使得蟻群算法搜索的側重點放在那些可能具有較高適應值的個體所在的區間內,以較大的概率收斂到全局最優解。因此,在“探索”和“利用”之間建立一個平衡點是蟻群算法研究的關鍵問題之一。
為了克服蟻群算法的這些缺陷,使它的性能更好,研究者們探索了信息素殘留因子(1-ρ)、信息啟發式因子、期望啟發式因子、信息素強度、螞蟻數目等蟻群算法的影響因素,并進行了改進[1-3]。高尚提出了混沌蟻群算法,采用混沌初始化改善個體質量和利用混沌擾動避免搜素過程陷入局部極值,實驗表明該算法提高了計算效率[4]。湯可宗等從參數的動態調整、信息量的更新規則、局部搜索策略進行相應的改進,引入信息素平滑機制,實驗表明該算法具有較好的收斂性和穩定性,能夠克服算法中早熟和停滯現象的過早出現[5]。王峰峰等提出了在蟻群算法中植入遺傳算法,利用遺傳算法生成信息素的分布,克服了蟻群算法中搜索時間長的缺陷,在蟻群算法尋優中,采用交叉和變異的策略改善了TSP解的質量,實驗表明該算法是有效的[6]。蔡榮英等提出了迭代改進蟻群算法,在構造解的過程中,螞蟻始終記憶一個完整的解,并只接受能夠改進解的候選城市,使用解的部分重構策略來保持種群的多樣性,避免早熟收斂,實驗表明該算法在更少的迭代次數中獲得更好的解[7]。其他學者也做出了相應的改進研究[8-10]。
文中提出一種改進蟻群算法,該算法在初始位置選擇和信息素更新機制兩方面進行改進,在相同參數下,改進后的蟻群算法的搜索時間大大縮短,而且得到了更好的最優解。將其應用到旅行商問題中,和其它兩種算法相比,其具有較好的搜索最優解的能力,對新解不會過早的終止,探索新解的能力進一步增強。
1 蟻群算法
1.1 蟻群算法的步驟
在求解TSP問題中,蟻群算法的具體實現步驟如下:
1)參數初始化。其中,令時間t=0,循環次數Nc=0,最大循環次數表示為Ncmax;將m個螞蟻置于n個城市上,則有向圖上每條邊(i,j)的初始化信息量τij=const,其中const表示常數,且初始時刻△τij=0。
2)循環次數 Nc←Nc+1。
3)螞蟻的禁忌表索引號k=1。
4)螞蟻數目k←k+1。
5)螞蟻根據狀態轉移概率公式(1.1)計算的概率選擇城市 j 并前進
6)修改禁忌表指針,即選則好之后將螞蟻移動到新的城市,并把該城市移動到該螞蟻個體的禁忌表中。
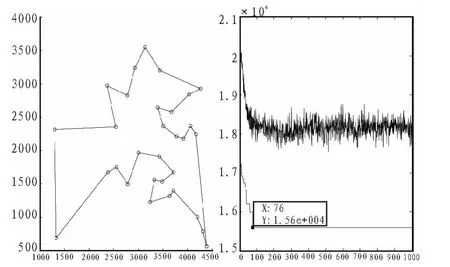
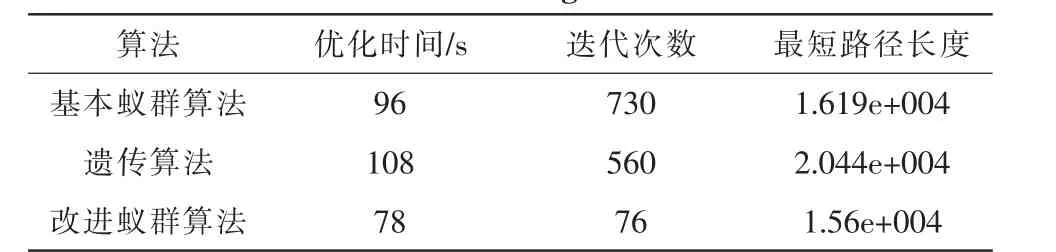
7)若集合C中城市未遍歷完,即k 8)根據公式(2)和式(3)更新每條路徑上的信息量。 9)若滿足結束條件,循環次數Nc>Ncmax,則循環結束并輸出程序計算結果,否則清空禁忌表并跳到第2)步。 α為信息啟發式因子,表示軌跡的相對重要性,反映了螞蟻在運動過程中所積累的信息在螞蟻運動時所起的作用,其值越大,則該螞蟻越傾向于選擇其他螞蟻經過的路徑,螞蟻之間協作性越強;β為期望啟發式因子,表示能見度的相對重要性,反映了螞蟻在運動過程中啟發信息在螞蟻選擇路徑中的受重視程度,其值越大,則該狀態轉移概率越接近于貪心規則;ηij(t)為啟發函數,其表達式為為相鄰兩個城市之間的距離。 t+n時刻在路徑(i,j)上的信息量按如下規則進行調整 : 式中,ρ為信息素揮發系數,1-ρ為信息素殘留因子,為了防止信息的無限積累,ρ的取值范圍為次循環中路徑(i,j)上的信息素增量,初始時刻為第k只螞蟻在本次循環中留在路徑(i,j)上的信息量。 1)初始位置的缺點 在蟻群算法中,螞蟻初始位置的選擇是隨機性的,這樣可能造成螞蟻的分布過于密集。在初始搜索時螞蟻依據城市間的路徑信息來選擇下次的搜索路徑,使得螞蟻都傾向于選擇在自己附近較短的路徑,這樣造成了局部收斂過快,得到較小范圍的解空間,對求解結果造成影響。 2)在信息素機制方面存在的缺點 ①算法初始化之后,螞蟻初始化位置是隨機選擇的,和各個城市間分布了相同的信息素初始濃度,這就造成了算法在開始搜索時的方向不確定性和求解的多樣性方面先天不足。 ②在螞蟻搜索過程中,信息素僅僅在所有螞蟻完成本次巡游時才會進行全局更新,從而造成搜索時間過長。 由于蟻群算法存在以上的缺點,文中從以上兩個方面進行改進,使其全局性與收斂速度都有明顯的提高。 對于初始化位置的確定,文中提出一種“螞蟻邊緣化”的初始位置選擇策略對初始位置進行優化。 此邊緣化的思想是將螞蟻放在所有城市的邊界位置,盡量打散螞蟻的密集點,這樣在初始時刻,螞蟻相互之間不會過早的影響。判斷一個離散區域的邊界位置是很困難的,因為它只提供各個城市的坐標信息,這些坐標信息直接可以得到任意兩城市的距離信息,這些信息只是一些抽象的數據,對于尋找城市的邊界信息是不夠的。這里提出一種近似的方法來確定邊緣城市。 此方法根據實際城市間距離的數據信息,將某城市和其他城市間的距離信息全部相加和為Si,將Si按照從大到小的次序排列,根據Si的大小判斷,最大的Si是離其他城市最遠的城市對應的和,其主要思想如下所示: 1)設有m只螞蟻要選擇初始位置,先將n個城市分別求出與其他城市間的距離之和將得到的Si按照從大到小順序排序; 2)即可確定最大的Si對應的城市即為距離其他城市最遠的,其他依次次之; 3)將螞蟻放在前m個Si對應的城市上,就實現了城市邊緣化的選擇。 在基本蟻群算法中,分別應用初始位置邊緣化和初始位置隨機選擇,比較2種方法的優劣。此處,城市規模為29,螞蟻數目為14,最大迭代次數為100,選取10次循環的平均值,α=1,β=5,ρ=0.7。 兩種方法的最后結果如表 1 所示。 表1 兩種初始化螞蟻算法的比較Tab.1 The comparison of two kinds of initialization ant algorithm 再次驗證螞蟻數目不同的情況下,兩種方法的性能優劣。 城市規模 48,螞蟻數目分別為 12、24、36、48,最大迭代次數1 000,選取10次循環的平均值,,。應用兩種方法的最后結果如表2所示。 表2 不同螞蟻數目下兩種方法的比較Tab.2 The comparison of the two methods under different number of ants 實驗結果分析如下: 1)通過表2看出,邊緣法比隨機法得到了更好的最優解均值,從最優解和最差解的差值可以看出,邊緣法的魯棒性更好。 2)通過表2的對比比較,當螞蟻數目增加時,邊緣法仍然比隨機法得到更好的解,但是,兩種方法得到的解的差別隨著螞蟻數目的增加越來越小,這是因為,隨著螞蟻的數目增加,越來越多的城市上被放置了螞蟻,兩種方法之間的差異逐漸減小,直到城市數目與螞蟻數目相同時,兩者之間再無差別,同時,算法搜索時間也會隨著螞蟻數目的增多而變長。 由以上分析可知,利用邊緣法確定螞蟻初始化位置確實強于隨機方法,對于要巡游的城市規模較大、搜索速率要盡可能快時,可以選擇邊緣法,同時將螞蟻數目為城市數目的3/4或者 1/2。 信息素在蟻群算法中的作用關系到算法能夠最終順利找到最優解的關鍵因素。信息素更新機制為螞蟻尋找最佳路徑提供了指導,對于蟻群算法解決靜態組合優化問題和動態組合優化問題這都是非常必要的。 本文對信息素的更新規則做了一些改進。首先,在初始化階段,對螞蟻初始化位置和各路徑上的信息素初始濃度分布按照某些規則進行分配,使之符合實際情況。其次,將螞蟻局部的信息素更新和全局信息素更新結合使用,通過精英選擇策略,在候選解上的螞蟻完成一次巡游之后,對它附近路徑的信息素就進行更新,其他路徑上的信息素不變化。 2.2.1 表格初始化信息素的分配的規范化 利用邊緣法可以對螞蟻初始化位置進行選擇,可以考慮將搜索路徑上的初始信息素濃度分配按照下述規則進行:在邊界的m個城市之間路徑上分配相同的信息素τ(0)=c;在余下的路徑上根據具體點的位置和求解問題類型的不同,可以通過下述公式確定余下的n-m個點中的某點x處的初始信息素大小: 式中,i是距離城市x處最近的邊緣城市位置,k、a均是大于零的常數,若為最小值問題,則a>1;若為最大值問題,則0 k、a的選擇應以具體情況而定,即保證算法能夠在更接近真實環境下尋優。 2.2.2 螞蟻全局路徑上信息素的改進 在基本的蟻群算法中,螞蟻只有在一個搜索周期結束后,才能完成一次信息素的更新。對于所有螞蟻走過的路徑,某些路徑上可能得到差的解,由于信息素的增加,此解可能變成假的最優解;當最優解還沒走過時,該路徑的信息素隨著蒸發量的變化變得越來越小,從而被忽略。則在下次搜索中,最優解對應的路徑被選取的概率越來越小,這樣造成了大量無效的搜索,使得運算速度降低。 文中采用以下的信息素更新算法:在全局路徑上,假設L(t)是螞蟻搜索了t次之后所得到的最佳路徑,L*(t)是螞蟻未走過的路徑,對所有螞蟻走過的路徑(i,j)∈Lk(t),t次尋優結束后,位置i到j間的路徑信息素更新量為△τij(t): 螞蟻沒走過的路徑的信息素更新量為: 其中,γ∈(0,1),f(t)為 L(t)對應的最佳目標值。 對于全局螞蟻走過的路徑,信息素的更新規則為: 對于螞蟻未走過的路徑的信息素更新規則為: 此規則減弱了已走過路徑的信息素更新速度,避免因為信息素增加過多而導致下次搜索的誤判,同時還增強了螞蟻未到達路徑的信息素更新速度,提高了搜素的效率。 以某物流配送中心的VRP系統為例驗證算法的效果,假設2輛載貨車的載重量8 T,向8個顧客送貨,顧客對貨物需求量為 gi(i=1,2,…,8),每條配送路徑的花費為 Ci,j(i,j=1,2,…,8),可得以下經驗數據如表3所示。 表3 物流配送中心配送路線成本表Tab.3 Distribution route cost table of logistics center 對蟻群算法和改進信息素的蟻群算法對上述配送路線進行優化,找到一條最佳的配貨路線,即路程最短或者代價最小。 算法中參數設置如下:α=2,β=5,ρ=7,螞蟻數目 60,迭代10次,實驗結果如表4所示。 表4 兩種蟻群算法的優化結果比較Tab.4 The comparison of two kinds of ant colony algorithm optimization 改進信息素蟻群算法最后求得的平均最優值是67.5,選擇的最優路線是:0-4-7-6-0-1-3-5-8-2-0,這比用基本蟻群算法求解得到的76.5要精確了很多,實驗證明改進算法在解決車輛路徑尋優問題具有很高的性能。 根據以上思想,該改進的蟻群算法流程可描述如下: 1)參數初始化。其中,令時間t=0,循環次數Nc=0,最大循環次數表示為Ncmax。 根據邊緣法初始化螞蟻位置的思想,將m只螞蟻放在前m個Si對應的城市上,此時有向圖上每條邊(i,j)的初始化信息量 τix(0)=ka-f(i-x)。 5)螞蟻根據狀態轉移概率公式(1)計算的概率選擇城市j并前進 6)修改禁忌表指針,即選則好之后將螞蟻移動到新的城市,并把該城市移動到該螞蟻個體的禁忌表中。 7)若集合C中城市未遍歷完,即k 8)當所有螞蟻完成本次搜索后,根據式(5)、(6)、(7)、(8)進行全局信息素更新。 9)若滿足結束條件,循環次數Nc>Ncmax,則循環結束并輸出程序計算結果,否則清空禁忌表并跳轉到第2)步。 為了檢驗算法的有效性和優越性,分別將基本蟻群算法、遺傳算法、改進的蟻群算法應用于31個城市TSP問題中進行仿真實驗。其中參數設置為:1)蟻群算法:螞蟻規模25,最大迭代次數1 000,信息素揮發系數0.7,信息素啟發式因子1,期望值因子5。2)遺傳算法:種群規模100,最大迭代次數1 000,交叉率0.9,變異率0.1。將TSPLIB31中各個城市的坐標給出,如圖1所示。 圖1 31個城市的坐標Fig.1 The coordinates of 31 cities 通過仿真得: 1)基本蟻群算法的最短路徑,其示意圖如圖2所示。 圖2 基本蟻群算法Fig.2 Basic ant colony algorithm 其最終優化路線為(數字代表TSP31城市坐標的標號):15-1-29-30-31-27-28-26-25-24-20-21-22-18-3-17-19-16-23-11-6-5-4-2-8-9-10-7-13-12-14。 2)遺傳算法的最短路徑,其示意圖如圖3所示。 圖3 遺傳算法最短路徑Fig.3 The shortest path of GA 其最終優化路線為: 5-6-9-8-7-3-1-4-15-18-25-27-26-10-11-28-30-29-24-19-23-13-31-14-12-20-21-17-2-16-22。 3)改進的蟻群算法的最短路徑,其示意圖如圖4所示。 圖4 改進蟻群算法Fig.4 Improved ant colony algorithm 其最終優化路線為: 14-12-13-11-23-16-5-6-7-2-4-8-9-10-18-1-17-19-3-24-25-20-21-22-26-28-27-30-31-29-15。 通過以上仿真,可以得到表5。 表5 利用幾種算法求解TSP31問題的試驗結果Tab.5 Experimental results of several algorithms for solving TSP31 分析以上實驗數據可見,改進后的蟻群算法具有較好的搜索最優解的能力。如對TSP31在原有蟻群算法上的最短路徑為1.619e+004,改進后的算法中得到的最短路徑為1.56e+004,在路徑演化過程中,改進的算法對新解不會過早的終止,探索新解的能力優化進一步增強。同時,在相同的參數下,改進后的算法不僅迭代次數大大減少、優化時間大大縮短,而且得到了更好的最優解。實驗表明,改進后的算法具有較好的性能。 文中在蟻群算法的基礎上,通過對初始位置選擇、信息素初始化分配和全局信息素三方面的改進,將其應用到求解TSP中,較有效的克服了蟻群算法中出現的搜索時間長、易停滯、收斂速度較慢等問題;從仿真結果來看,該算法在求解性能和時間性能方面都取得了很好的結果,從而實現了TSP問題的優化,為解決一些組合優化問題提供了一定的參考。 [1]Duan H B,Wang D B,Yu X F.Research on the optimum configuration strategy for the adjustable parameters in ant colony algorithm[J].Journal of Communication and Computer,2005,2(9):32-35. [2]葉志偉,鄭肇葆.蟻群算法中參數設置的研究-以TSP為例[J].武漢大學學報,2004,29(7):597-601.YE Zhi-wei,ZHENG Zhao-bao.Research on the ant colony algorithm parameter settings-to TSP Case[J].Wuhan University,2004,29(7):597-601. [3]詹士昌,徐婕,吳俊.蟻群算法中有關算法參數的最優選擇[J].科技通報,2003,19(5):381-386.ZHAN Shi-chang,XU Jie,WU Jun.Ant colony algorithm,the optimal choice of algorithm parameters related[J].Technology,2003,19(5):381-386. [4]高尚.解旅行商問題的混沌蟻群算法[J].系統工程理論與實踐,2005,25(9):100-104.GAO Shang.Chaos ant colony algorithm for traveling salesman problem[J].Systems Engineering Theory and Practice,2005,25(9):100-104. [5]湯可宗,江新姿,張磊,等.一種求解旅行商問題的改進蟻群算法[J].華東理工學院學報,2007,30(4):387-391.TANG Ke-zong,JIANG Xin-zi,ZHANG Lei,et al.Improved ant colony algorithm for solving traveling salesman problem[J].East China Institute of Technology,2007,30(4): 387-391. [6]王峰峰,王仁明,伍佳.求解TSP問題的一種改進蟻群算法[J].控制理論與應用,2010,29(7):1-3.WANG Feng-feng,WANG Ren - ming,WU Jia.TSP problem an improved ant colony algorithm [ J].Control Theory and Applications,2010,29(7):1-3. [7]蔡榮英,王李進,吳超,等.一種求解旅行商問題的迭代改進蟻群優化算法[J].山東大學學報:工學版,2012,42(1):6-11.CAI Rong-ying,WANG Li-jin,WU Chao,et al.Solving Traveling Salesman Problem iterative improvement ACO[J].Shandong University :Engineering Science,2012,42(1):6-11. [8]陳永強.人工蟻群算法及其在組合優化中的應用[D].哈爾濱:哈爾濱工業大學,2003. [9]馬良,項培軍.螞蟻算法在組合優化中的應用[J].管理科學學報,2001.4(2):32-36.MA Liang,XIANG Pei-jun.Ant algorithm in combinatorial optimization[J].Journal of Management Sciences,2001.4(2):32-36. [10]葉志偉,鄭 葆 .蟻群算法中參數α,β,ρ設置研究-以TSP為例 [ J ].武漢大學學報,2004,29(7):597-601.YE Zhi-wei,ZHENG Zhao-bao.Ant colony algorithm parametersα,β,ρ,set - A case study TSP [J].Wuhan University,2004,29(7):597-601.

1.2 蟻群算法的缺點
2 改進的蟻群算法
2.1 初始位置選擇


2.2 信息素更新規則的改進

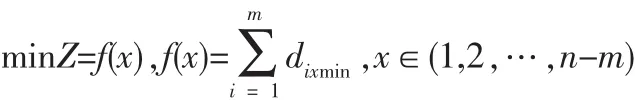






2.3 改進蟻群算法的流程

3 改進蟻群算法在TSP中的應用



4 結論

