海運集裝箱空箱調運優化模型及算法研究

徐麗蕊，李 靜

（陜西工業職業技術學院 汽 車與物流學院，陜西 咸 陽 7 12000）

隨著全球經濟的一體化，集裝箱運輸作為一種先進、規范的運輸方式，在經濟貿易中的重要性越來越顯著。然而，伴隨著集裝箱運輸的高速發展，空箱調運問題也日益突出，并已經成為船公司集裝箱管理中一個需要迫切解決的重點問題。空箱調運計劃的好壞對船公司航線的用箱量、租箱量有直接影響，也與集裝箱運輸成本密切相關。據統計，當前全球海運集裝箱運量中的空箱比例約占總運量的 20%，甚至某些船公司的空箱運輸量超過了這一比例，每年全球空箱調運費用超過300億美金。如何更加科學、合理、經濟地進行集裝箱的空箱調運已成為提高集裝箱運輸效率、降低運輸成本的一個重要因素[1]。

針對海運集裝箱空箱調運問題，國內外的學者進行了廣泛的研究。李大海[2]通過對集裝箱流轉機制的分析，總結了控制空箱調運成本的核心；施欣[3]分析了海運集裝箱空箱調運過程，建立了集裝箱優化模型；劉恒江和徐劍華[4]通過分析集裝箱空箱調運的現狀，提出了解決這一問題的新方法；韓曉龍，張盟學[5]建立了基于集裝箱制造商合作的集裝箱空箱調運優化模型，并對該模型進行了求解。

本文在上述研究的基礎上，考慮航運公司集裝箱空箱調運費用和租賃費用，建立了總成本最小的數學模型，通過LINGO編程，能夠求得此問題的最優解。

1 集裝箱空箱調運問題

一般空集裝箱的調運流程如下[6]：

顧客領取空箱后，進行貨物裝載，在船舶離港前將載貨集裝箱即重箱運到港口，在港口集裝箱被裝上船舶并運往目的港；船舶到達目的港后，重箱被送至收貨人處，收貨人領取自己的貨物，然后將空箱返回；返回之后的空箱就可以用來滿足其他顧客的需求或者被儲存，成為庫存集裝箱，用來滿足本港口顧客的空箱需求或被調運用來滿足其他顧客對空箱的需求。

空箱調運問題要解決就是集裝箱需求與供應之間不平衡現象。從經濟學角度來看，在某個時期內，某地集裝箱的供應量大于需求量，而在另一時期內，該地集裝箱的供應量小于需求量，因此，前者空箱調運問題的重點是怎樣調運、何時調運、調運多少集裝箱，以滿足需求地的需要或以備后期的需要；后者要考慮的重點則是如何從其他地方調運空箱以滿足需要。集裝箱空箱調運核心在于解決何時、從何處、調運多少空箱到需求地，是控制和決策空箱從供應地到需求地的流動的活動。

2 集裝箱空箱調運模型

2.1 求解目標

靜態確定性空箱調運模型假定以下要素確定：空箱的供給量和需求量、貨船容量（即重箱運輸量）、過剩的空箱數量和運輸時間。

該空箱調運模型是針對某條航線經營人進行設計的，即以航線經營人為主體，分析該航線上集裝箱空箱的分配和調運情況。

該模型的目標是在首先滿足重箱運輸的前提下，使空箱運輸和租賃的總費用達到最小，其總費用包括在不同供給點和需求點間調運空箱的費用以及空箱租箱費。

2.2 模型的假設條件

1）假設航班和船期表固定不變并且已知；

2）假設可以預先確定計劃期內的需求港和供給港；

3）假設航線上每個港口的空箱運輸費率、租賃費等都是已知的。

4）假設每個港口的空箱庫存量和需求量已知。

若某航運公司航運區域共有m+n個港口，定義供給港為空箱現存量大于港口空箱需求量港口，共m個，并記每個港口可調用的空箱量分別為記需求港為空箱現存量小于港口空箱需求量的港口，共n個，其缺箱量分別記為 D1，D2，···，Dn。

5）假設在任何時間、任何港口租賃空集裝箱都沒有數量的限制。

6）假設在規定的計劃期內進行優化決策。

7）假設集裝箱箱型單一，不考慮集裝箱中轉。

2.3 模型的建立

空箱調運和租賃總費用最小的海運空箱調運問題靜態確定性模型如下：

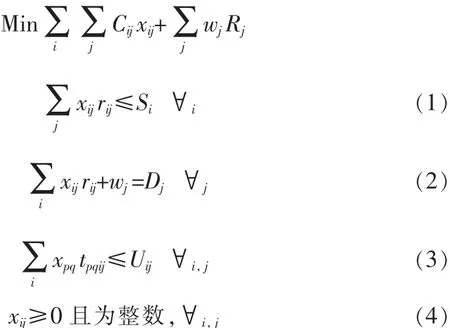
式中：

i∈S，S為供應港的集合；

j∈D，D為需求港的集合；

Cij——從港口i到港口j的運輸費；

xij——從港口i到港口j的運量；

rij表示在所有航線上供應港到需求港是否可達

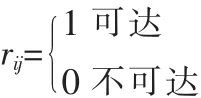
wj——需求港j的租箱量

Rj——港口j的租箱費用率

Si——港口i的空箱供給量

Dj——港口j的空箱需求量

Uij——港口i，j之間的空箱運力。Uij=船舶的運輸能力即箱重量

當航次[p，q]段?[i，j]段時，tpqij=1，否則 tpqij=0。

在模型中，xij、wj為決策變量。

因此目標函數為不同供給點和需求點間調運空箱的費用以及空箱租賃費用之和最小。

約束條件的含義如下：

約束條件1）表示對任何一個供應港來說，向所有需求港供應的空箱總量不能超過該港口的最大空箱供給量；

約束條件2）表示對任何一個需求港來說，從需求港調運的空箱與其租用的集裝箱之和應等于該港口對空箱的需求量，以保證滿足需求；

約束條件3）表示任意兩個港口之間的運量都不超過該航段的空箱運力；

約束條件4）表示從港口到港口的運量取為整數。

3 算例分析

集裝箱運輸中班輪運輸通常的間隔時間通常為一周，因此，本算例的集裝箱空箱調運計劃時間間隔取為7天進行一次，按照每次空箱調運計劃的時間來確定每個港口的重箱預出口量和空箱現有量，然后求出各港口的空箱需求量，再根據各港口對空箱的需求量和供給量，確定本周的需求港和供應港，最后通過模型和LINGO程序求得空箱的調運方案。

1） 假設 D1、D2、D3、D4和 D5為需求港，S1、S2、S3和 S4為供給港，各航線掛靠順序如圖1所示。

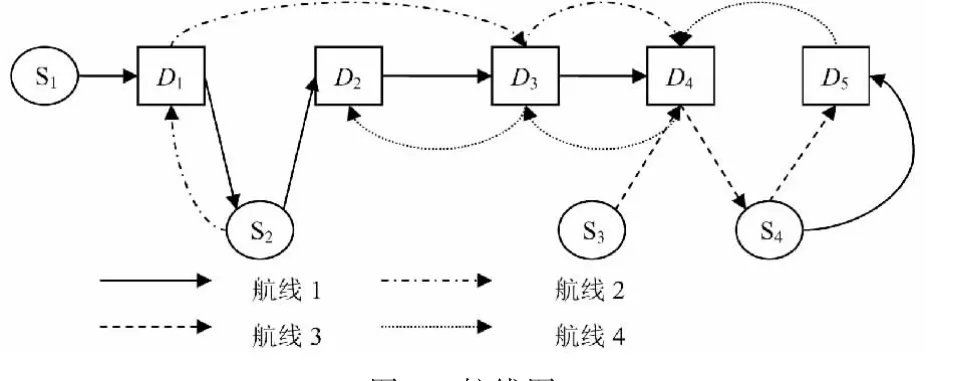
圖1 航線圖Fig.1 Chart the ships route

根據 tpqij的定義，當航次[p，q]段?[i，j]段時，tpqij=1，否則tpqij=0。對上述航線圖，可求得tpqij的值如下表1所示。

2）各供應港的供應量如表2所示。

3）各需求港的需求量如表3所示。

4）任意兩個港口之間的運輸費如表4所示。

5）需求港和供應港間的可達性如表5。

6）各港口間航線上的空箱運輸能力如表6所示。

7）租箱費率如表7所示。

4 模型運行結果

結合線性規劃求解軟件Lingo的語言語法，根據該空箱調運問題的目標函數和約束條件，其優化程序代碼如下：

MODEL:

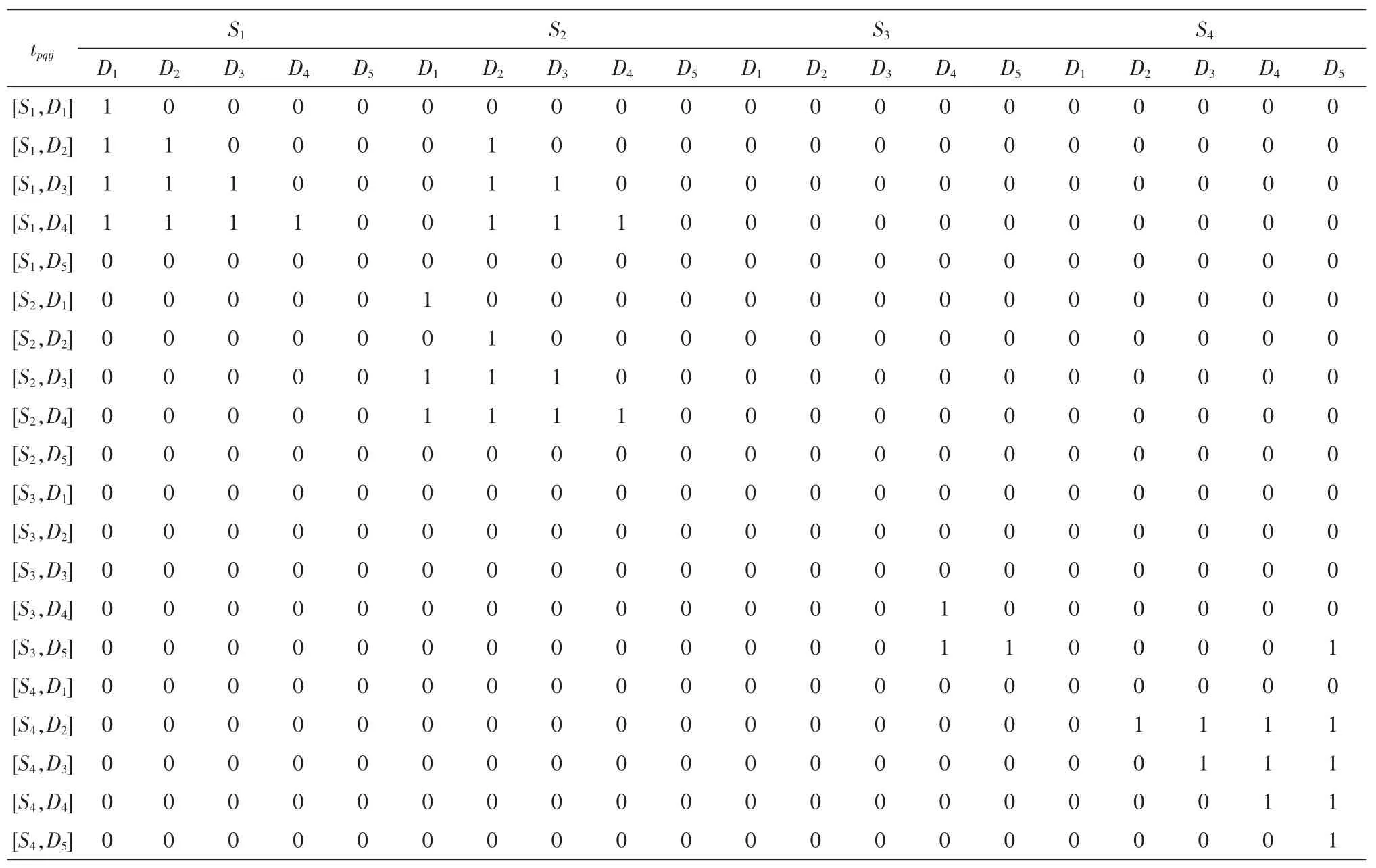
表1 值表Tab.1 The table of value

表2 港口i的空箱供應量 TEUTab.2 Supply of empty containers in the port i TEU

表3 港口j的空箱需求量 TEUTab.3 Demand of empty containers for port j TEU

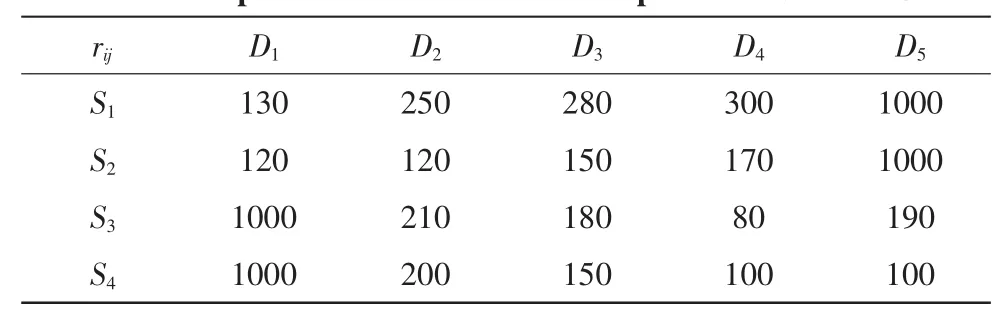
表4 港口間的運輸費 美元/TEUTab.4 Transportation costs between the ports U.S.dollar/TEU

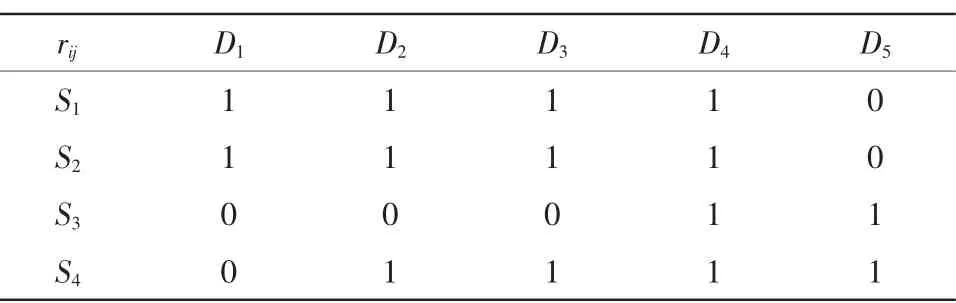
表5 值表Tab.5 The table of value

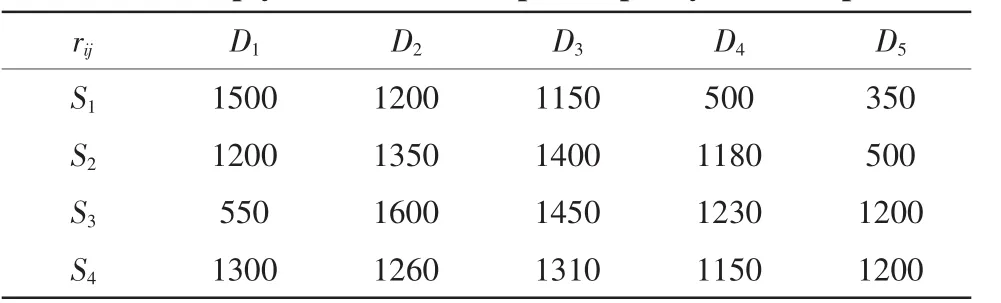
表6 港口間的空箱運輸能力Tab.6 Empty containers transport capacity between ports

表7 租箱費率表Tab.7 Leasing rate table

SETS:

GY/1..4/:S；

XQ/1..5/:D，W，R；

CXC（GY，XQ）:COST，X，U，RR；

CCXCC（CXC，CXC）:T；

ENDSETS

MIN=@SUM（ CXC（I，J）:COST（I，J） *X（I，J））+@SUM（XQ（J）:W（J） *R（J））；

@FOR（GY（I）:@SUM（XQ（J）:X（I，J）*RR（I，J））<=S（I））；

@FOR（XQ（J）:@SUM（GY（I）:X（I，J）*RR（I，J））+W（J）=D（J））； @FOR （CXC （I，J）:@SUM （CCXCC （CXC （P，Q），CXC（P，Q））:X（P，Q）*T（P，Q，I，J）<=U（I，J）））；

END

通過數學規劃求解軟件Lingo8.0進行數據初始化，并計算求解，得到目標函數值為713 680。因此，在此計劃期內空箱的調運方案如下：具體求解結果見表8所示。

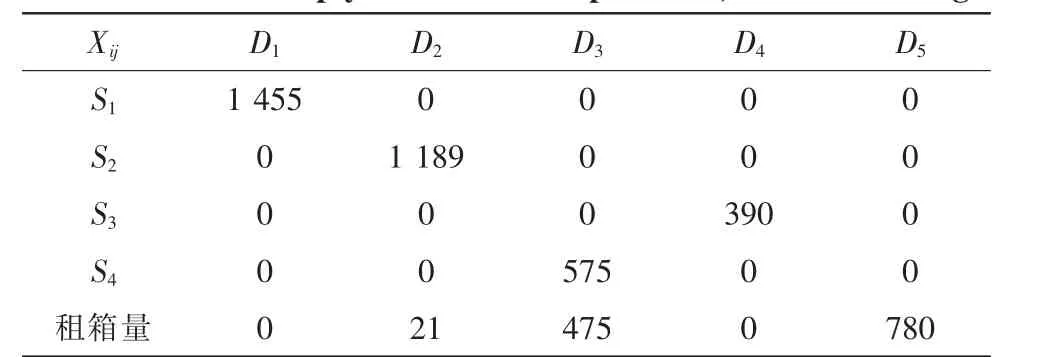
表8 空箱調運、租箱情況表Tab.8 Table of empty container transportation,container leasing

即從供應港S1調運1 455個空箱到需求港D1，從供應港S2調運1 189個空箱到需求港D2，從供應港S4調運575個空箱到需求港D3，從供應港S3調運390個空箱到需求港D4。各需求港的租箱方案如下：需求港D2租用空箱21，需求港D3租用空箱475，需求港D5租用空箱780，需求港D1和D4無需租箱。

從各港口間的運輸費用可以看出，供應港S1到需求港D1調運的成本最小，從供應港S2到需求港S2的調運成本最小的。從優化方案中可以看出，需求港D1的空箱需求全部由供應港S1來滿足，需求港D2的空箱需求也全部由供應港S2來滿足。因此，在具備空箱調運可行性的前提下，在空箱調運方案中運輸成本將起到決定性的作用。

5 結束語

在碼頭集裝箱作業中，集裝箱空箱調運是一個非常重要的作業環節。在分析集裝箱空箱調運問題的基礎上，以空箱調運費用和租賃費用總和最小為目標，建立的空箱調運模型能夠比較合理地反映航線的實際特點，通過編寫LINGO程序代碼，利用LINGO軟件可以快速求解該問題。最后用實例表明，該數學模型和求解程序的可行性和有效性，為碼頭集裝箱箱務管理提供了一種快速有效的空箱調運方法。

[1]尚芯新.集裝箱空箱調運優化問題研究[D].大連：大連海事大學，2011.

[2]李大海.海運集裝箱空箱調運成本控制研究[J].現代商貿工業，2013（12）：53-54.LI Da-hai.Cost control of empty container shipping containers[J].Modern Business Trade Industry，2013（12）：53-54.

[3]施欣.集裝箱海運空箱調運優化分析[J].系統工程理論與實踐，2003（4）：70-89.SHI Xin.The optimization of sea-bound empty container distribution[J].Systems Engineering-theory&Practice，2003（4）：70-89.

[4]劉恒江，施欣.給予Petri網的集裝箱空箱調運方針分析[J].交通運輸工程學報，2002，2（3）：97-102.LIU Heng-jiang，SHI Xin.Simulation ofcollection and allocation of emptycontainers based on Petri net[J].Journal of Traffic and Transportation Engineering，2002，2（3）：97-102.

[5]韓曉龍，張盟學.集裝箱空箱調運優化模型[J].集美大學學報：自然科學版，2013，18（2）：114-118.HAN Xiao-long，ZHANG Meng-xue.Optimization model on empty container allocation based on the container manufacturers[J].Journal of Jimei University：Natural Science，2013，18（2）：114-118.

[6]陳心德，姚紅光.集裝箱運輸與國際多式聯運管理[M].北京：清華大學出版社，2008.

[7]李秀芬.基于LINGO軟件的鐵路集裝箱空箱調運優化研究[J].企業基礎開發，2013，32（1）：6-8.LI Xiu-fen.Research on railway empty container distribution based on LINGO software[J].Technological Development of Enterprise，2013,32（1）：6-8.