基于壓縮感知的水聲數據高效傳輸及其仿真

張 斌，徐志京

（上海海事大學 信息工程學院，上海201306）

水聲通信是當前唯一可在水下進行遠程信息傳輸的通信形式,由于其在民用和軍事上都有重大意義,水聲通信的研究一直是國內外研究的熱點。水聲信道是水聲通信技術遠遠滯后于陸地無線系統的最大障礙，由于水聲信道特有的雙擴特性，即多途擴展和多普勒擴展，以及頻率選擇性衰落等都影響著水聲數據的有效傳輸[1]。它不但對目標信號進行能量變換（聲傳播損失），而且它對聲源的發射波形也進行變換，因而聲信道可以看作是對發射波形進行變換的濾波器，可以用時變、空變的隨機濾波器來表示[2]。因此，這給水聲數據的傳輸及研究帶來了很大的困難，然而，壓縮感知（CS）理論的提出，能夠在采樣端采樣少量的數據就能恢復原始數據，為解決水聲信道數據傳輸量限制問題奠定了堅實的理論基礎，減輕了信道傳輸壓力；正因為水聲信道特有的稀疏性特性，國內外有不少學者研究了基于壓縮感知的OFDM水聲信道估計，他們采用OFDM調制技術有效地降低了多途擴展給信道估計帶來的影響，利用壓縮感知技術應用在稀疏信道估計中，提高了信道的估計精度，同時改善了系統的性能、降低了系統均衡的復雜度[3]。

1 研究方案

文中基于上述的研究現狀以及理論背景，提出了一種基于壓縮感知的水聲數據傳輸方案，將壓縮感知理論應用在水聲數據的傳輸中，采用網絡時延，誤碼率以及信道利用率等參數和傳統傳輸方案進行比較來驗證其傳輸的高效性，傳統及改進的傳輸系統方案框圖如下所示。

圖1 傳統傳輸系統方案框圖Fig.1 Traditional transmission system block diagram

圖2 改進方案框圖Fig.2 Improved plan block diagram

其中，x(t)是原始數據序列，經過壓縮感知處理后，原數據序列經過水聲modem調制，信號經過變換，在具有相干多途衰落的水聲信道中傳輸，在接收端進行數據的解調，得到x~(t)′信號，最后使用重構算法重構數據得到信號 x(t)′，與原數據x(t)進行對比，得到其誤碼率數據。

水聲信道中傳輸的數據可以是一些文檔、二進制脈沖信號等訓練序列，因其本身不占太大的存儲空間，適于在水聲信道中傳輸，可以作為實驗的原始數據進行一系列的實驗。

2 壓縮感知理論

2.1 稀疏表示

假設一個實值的、有限長度的一維離散時間信號x，它可以被看作為 RN空間中 N*1維矢量，規定 x[n]，n=1,2,…,N。任何在RN中的信號都可以表示成N*1維矢量集中的一個基。簡便起見，假定這個基是正交的。使用N*N基矩陣作為列，信號x就可以表示為

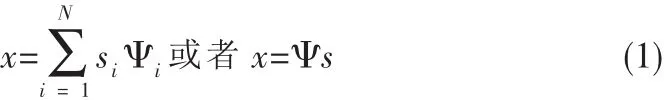
如果信號只有K維基矢量的線性結合的話，那么信號x是K稀疏的；也就是在公式(1)中Si互相關部分的K個元素是非零的，其它N-K個為零。這里的K＜＜N。那么就可以認定x是可壓縮的即可稀疏化的。

2.2 測量矩陣

觀測矩陣設計的目的是為了采樣得到M個觀測值，并保證從中能夠重構出原來長度為N的信號x或者稀疏基下的稀疏向量α。

觀測的過程就是利用M*N維觀測矩陣的M個行向量對稀疏向量進行投影，得到M個觀測值，即

圖3 觀測矩陣的圖形表示Fig.3 Graphical representation of the observed matrix

從上式中求出α是一個線性規劃問題，但由于方程的個數少于未知數的個數M＜＜N，這是一個無窮解的問題。

但如果x具有稀疏性，則有可能求出確定解。Candes、Tao等人提出必須保證觀測矩陣不會把兩個不同的K項稀疏信號映射到同一個采樣幾何中[4]，這就要求從觀測矩陣中提取的每個列向量構成的矩陣是非奇異的。這跟有限等距條件（RIP）的要求是一致的。

R.Baraniuk將上述條件簡化為如果保證觀測矩陣和稀疏基不相干[5]，則在很大概率上滿足RIP性質，不相干是指Ψ不能用Ψi｛｝稀疏表示，不相干性越強，互相表示時所需的稀疏就越多。

3 基于CS下水聲數據處理研究

3.1 基本原理

水聲數據的高效傳輸，是指在水聲信道容量受限情況下，利用現有的壓縮感知（CS）技術對數據進行一個預處理，首先發送端對要發送的數據進行壓縮，大大減小要發送的數據量，能夠在已知信道容量的前提下，把數據發送到接收端，同時保證網絡的時延不能太大，誤碼率控制在合理的范圍內，這些都是需要解決的瓶頸問題，最后接收端利用現有的一些重構算法對數據進行重構還原，保證數據的完整性。

3.2 CS的重構算法

本文采用基于l0范數的貪婪算法，即OOMP算法，該算法是最優正交匹配追蹤算法，其代替OMP算法中的原子選擇準則，而且其重構速度快，效率比較高，下面對OOMP算法進行簡單描述，具體見參考文獻[6]。

假設Ψλ1是從原子集合｝中選擇的一個原子，定義定義 Wi+1為 V1在 Vi+1上的正交補，那么在Vi+1上的正交投影算子可以表示為

由于 Ψλi+1∈Vi+1，若記 φi+1為 Ψλi+1在 Wi+1上的正交投影，則有

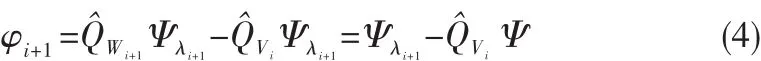
則信號υ在Wi+1上的正交投影算子可以寫成：

下面給出Vi+1正交投影算子的函數表達方式。

論文文獻[6]中證明了υ在空間Vi+1上的正交投影為

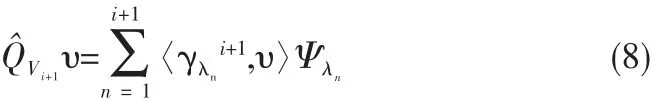
OOMP算法的原子選擇準則為：在i+1次迭代中選擇出是的新的冗余S~i+1模達到最小的原子Ψλi+1，由

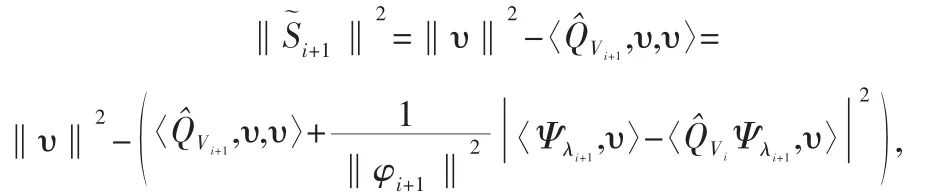
且因為前次迭代中〈Q^Vi,υ,υ〉已固定，所以最小化‖S~i+1‖2即為最大化函數en，這里有

3.3 研究方法

文中使用Simulink仿真軟件來實現水聲數據的高效傳輸及信道建模，仿真系統一共可以分為以下6個模塊：

1)信源模塊

2)CS壓縮處理模塊

3)信道模塊（調制解調）

4)CS重構模塊

5)信宿模塊

6)網絡時延模塊

Simulink仿真的整個傳輸系統如圖4所示。

為了作對比，將傳統的水聲數據傳輸框圖附上，如圖5所示。

以下分別對各個模塊作介紹：

首先是信源模塊，信源模塊采用伯努利信號發生器產生二進制序列。信號發生器發出信號，等概率發送0和1，幅值為1。

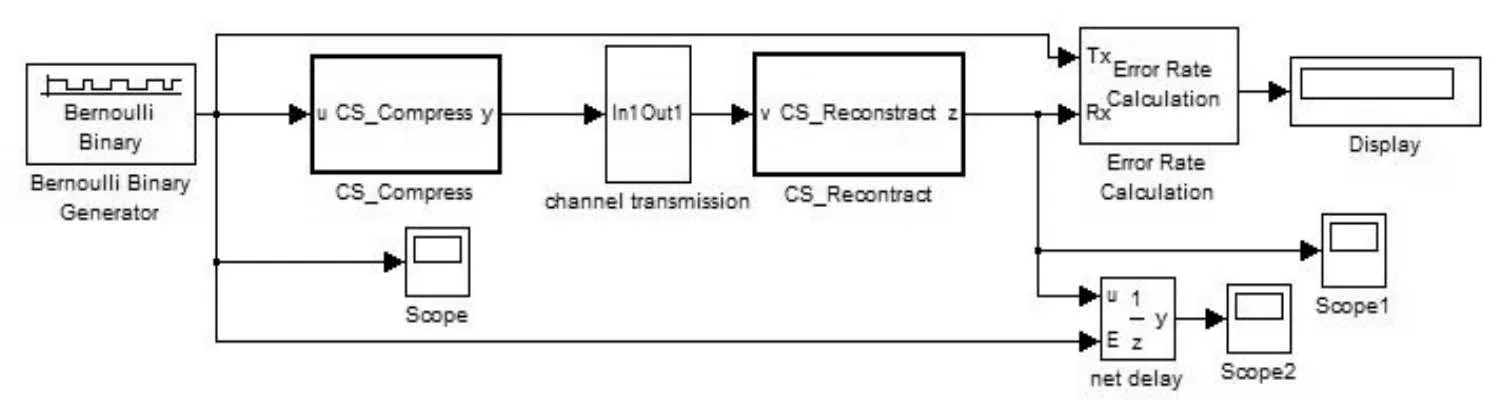
圖4 水聲數據傳輸系統（CS）Fig.4 Acoustic data transmission system（CS）

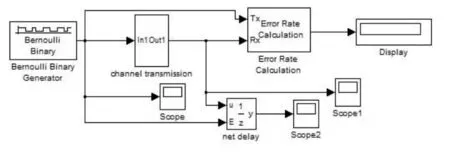
圖5 水聲數據傳輸系統（傳統）Fig.5 Acoustic data transmission system(traditional)

第二部分是CS壓縮處理模塊，完成對原始信號的壓縮，以及設計合適的觀測矩陣。

第三部分是信道模塊，上圖中對信道模塊進行了封裝，信道采用AWGN信道，輸入In1，輸出Out1。

其中，調制解調采用MSK系統。選用MSK系統的初衷在于MSK是一種特殊的2FSK(二進制頻移鍵控)，這種調制方式能使數據信號相位連續，包絡恒定，進而減小了誤碼傳輸，提高了傳信效率。

第四部分為CS重構模塊，重構模塊采用OOMP算法，對投影到觀測矩陣中的信號進行重構。

第五部分為信宿及誤碼率模塊

最后一部分是計算網絡時延模塊，計算整個網絡的從發出原信號到信宿接收到信號的網絡處理時延。

4 仿真結果

重構數據使用OOMP算法，對這兩種方案分別進行仿真。仿真對比的幾個參數如表1所列。

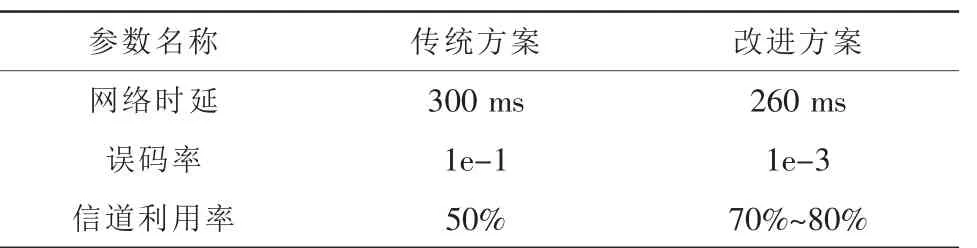
表1 仿真實驗結果Tab.1 The result of simulation test

軟件仿真結果圖如下所示。

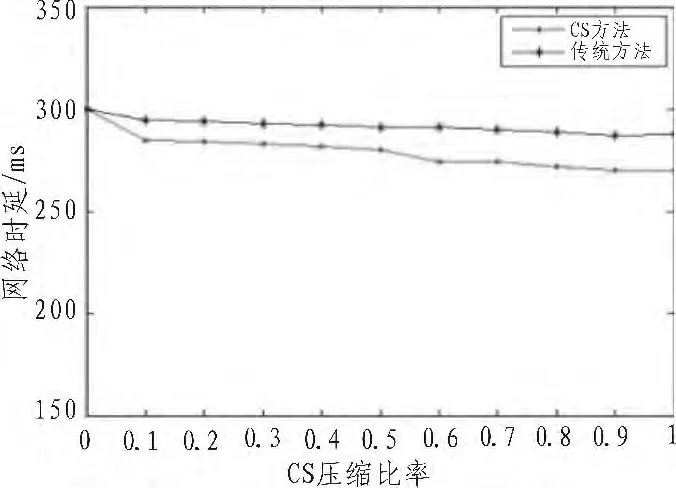
圖6 網絡時延對比圖Fig.6 Net delay comparison chart

從圖6中可以看出，隨著CS壓縮比率M/N的提高，水聲信道平均時延傳統方法變化不大；而經過壓縮感知處理后，網絡時延較傳統方法有了很大的改善，下降趨勢明顯。

從圖7可以看出，在信噪比SNR在（1，10）區間內時，兩種方法下的SNR對比沒有多大變化，在信噪比大道≥10 dB時，壓縮感知處理后的數據經過信道傳輸后誤碼率較傳統方法傳輸有明顯地下降。

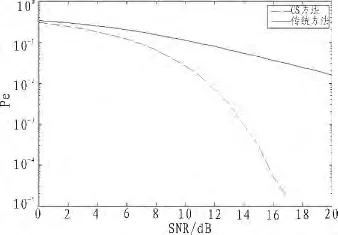
圖7 誤碼率對比圖Fig.7 BER comparison chart

信道利用率方面，由于采用了壓縮感知處理，水聲數據經過了一定的壓縮，單位時間內信道的利用率有了一定的提高，提升了信道的性能，如圖8所示。

5 結論

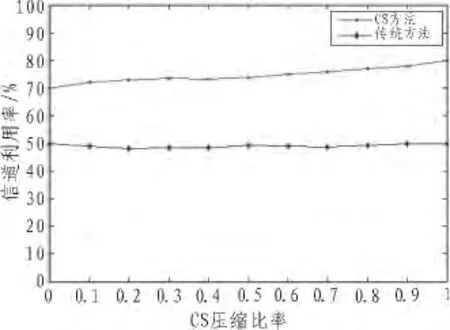
圖8 信道利用率對比圖Fig.8 Channel utilization rate comparison chart

水聲信道通常表現出稀疏性，文中針對這個特點對水聲數據發送之前進行壓縮感知處理，將CS理論應用在水聲數據的傳輸上；仿真實驗結果表明基于OOMP算法重構數據具有較低的誤碼率，相比較傳統的傳輸方案有一個很大的提高，同時，網絡時延明顯地減少，信道利用率有一定的提高，由此可以得出該方案驗證了本文要論證的高效性。

[1]殷敬偉.水聲通信原理及信號處理技術[M].國防工業出版社,2011.

[2]惠俊英,生雪莉.水下聲信道[M].哈爾濱：哈爾濱工程技術大學,2011.

[3]夏光輝,范巍巍.基于壓縮感知技術的水聲OFDM通信系統稀疏信道估計技術[C]//.2012中國西部聲學學術交流會論文集，2012.

[4]Emmanuel J,Candès,Michael B.Wakin.An Introduction to Compressive Sampling[J].IEEE Signal Processing Magazine.2008.

[5]Richard G,Baraniuk.Compressive Sensing[J].IEEE Processing Magazine.2007.

[6]Rebollo-NeiraL,Lowe D.Optimized orthogonal matching pursuit approach [J].IEEE Signal Processing Letters,2002,9(4)：137-140.