基于分組的STL模型快速切片算法

侯聰聰，南 琳，張 磊

(1.中國科學院沈陽自動化研究所，沈陽 110016；2.中國科學院大學，北京 100049)

0 引言

快速成型技術RP( Rapid Prototyping ) 是集機械、計算機、光學、電子及新材料為一體的新型先進制造技術，通過逐層增加材料制造零件[1,2]。在所有的RP工藝中，無論是由CAD造型軟件還是由逆向工程生成的零件CAD模型，都必須經過分層處理才能將數據輸入到RP設備中，因此分層算法是RP制造中的一個關鍵環節。

STL文件是RP系統中數據交換的標準文件類型[3]，用三角網格面近似地表現三維CAD模型，并記錄模型中每個三角面片的幾何信息，包括三角面片所在平面的法矢和它所包含的三個頂點的坐標。由于STL模型數據格式簡單、易于交換處理，基于STL模型的切片處理已被大多數RP系統采用。

目前，STL模型的切片算法主要分為以下兩類：

1）基于幾何拓撲信息的STL模型切片算法[4～8]。該類算法根據三角面片的點、邊和面數建立STL模型的整體拓撲信息，利用拓撲信息可以迅速查找到相鄰三角面片，并通過對相鄰三角面片的追蹤得到有向輪廓線。其優點是利用拓撲關系，無需排序，可直接獲得首尾相連的封閉輪廓線。但該算法也存在一定局限性：獲取STL模型整體拓撲信息的過程相當費時，尤其對于復雜的STL模型占用系統資源較多；當STL文件有錯誤時，可能無法得到正確的截面輪廓線。

2）基于三角面片幾何特征的STL模型切片算法[9～12]。該類算法根據三角面片頂點坐標沿切片方向投影值的大小進行分組排序，減少三角面片與切片平面位置關系的判斷次數，加快分層處理速度。但是該算法的局限性在于：對大量三角面片的排序是一個耗時的過程；在后續輪廓線的生成過程中，還要進行交線連接關系的搜索判斷；三角面片分組界限比較模糊，經常無法判斷三角面片與分層平面的位置關系。

針對以上兩種分層算法的優缺點，本文提出整體分組排序，局部建立基于鏈表的拓撲關系的思路以進一步的降低分層算法的復雜度。針對具體的零件模型，通過仿真對比分析，得到合適的分組組數。同時本文提出了基于鏈表的STL文件拓撲重建算法，在建立拓撲關系的同時去除了冗余數據，節省了存儲空間，提高了存儲效率。

1 基于鏈表的拓撲重建算法

STL文件的數據量很大，一個表面復雜的實體模型由幾萬甚至幾十萬個三角形面片構成，由于對任意多面體，均存在歐拉公式F-E +V=2，其中F表示面的數目，E表示邊的數目，V表示點的數目。對于一個由三角面片構成的多面體，每個三角面片具有3條邊，每條邊被2個三角面片共享，因此可得出E=3F/2。將其帶入歐拉公式得V=F/2+2，而STL文件中所存頂點數是三角面片數的3倍，所以平均分裂后的點數為原拓撲點數的6倍。因此數據的冗余現象比較嚴重。如果簡單地照原樣提取數據，會占用大量的計算機資源，降低計算速度，而且使得后續的處理計算量增大。因此從文件中提取數據時必須進行數據篩選，去除冗余信息。因而，STL文件拓撲重建過程通常由兩部分組成：冗余數據的去除和拓撲結構的建立。

本文提出了基于鏈表的STL文件重建算法。該算法采用鏈表[13]作為數據結構，將兩部分融合為一個整體，對冗余點和冗余邊進行了處理，實現了數據的無重復存儲。節省了存儲空間，提高了存儲效率，同時建立了拓撲結構，提高了數據的可操作性，為后續分層奠定了基礎。

1.1 拓撲重建的數據結構

拓撲重建過程數據結構分為三類，面（ Facet）、邊（Edge）和頂點（Vertex），由三個類產生三個對象，并建立相應的對象鏈表。為了節省拓撲關系存儲的時間和空間，頂點鏈表只記錄該點的坐標，邊鏈表只記錄所包含的頂點在頂點鏈表中的編號和所屬面片在面鏈表中的編號，面鏈表只記錄所包含的邊在邊鏈表中的編號。具體的數據結構如圖1～圖3所示。

1.2 拓撲結構重建

本算法以三角面片為基本單位，依次讀取每個三角面片的頂點數據，對頂點鏈表中的頂點進行查詢，在判斷一個頂點為非冗余點后，將其插入頂點鏈表并為其建立鄰域信息，并在插入了其他點后對其進行實時更新；以同樣方法進行邊的去冗余及建立鄰域信息，最終建立一個完整的拓撲結構。

算法具體步驟如下：FaceCount為STL文件中的三角面片個數總和。

Step1：分別創建點對象鏈表vlist、邊對象鏈表elist及面對象鏈表f l ist。

Step2：創建三個點對象v1、v2、v3，三條邊對象e1、e2、e3和面對象f，并將f添加到flist，取三角面片三個頂點數據，分別賦給v1、v2、v3。

Step3：取v1，查找vlist中是否有相同的點。如果有，則將該點在vlist中對應的索引號賦給e1的EVertexIndex1、e3的EVertexIndex2；如果沒有，則將v1添加到vlist，并將v1在vertexlist中對應的索引號賦給e1的EVertexIndex1、e3的EVertexIndex2。v2和v3同v1。

Step4：取e1，查找elist中是否有相同的邊，如果有，則將該邊在elist中對應的索引號賦給f的FEdgeIndex1，同時將f在flist中的索引號賦給該邊的EFacetIndex2；如果沒有，則將e1添加到elist，并將e1在elist中對應的索引號賦給f的FEdgeIndex1，同時將f在flist中的索引號賦給e1的EFacetIndex1。e2和e3同e1。

Step5：讀第n個三角面片，如果n≤ FaceCount，則返回step2；否則退出程序，拓撲結構創建完成。

1.3 算法復雜度分析

圖1 頂點鏈表

圖2 邊鏈表

圖3 面鏈表

該算法的時間復雜度主要是冗余點和冗余邊的濾除時間。對于上述算法，設STL文件中三角面片個數為n，則頂點數和邊數均為3n。依據上述STL文件中三角面片的公式E=3F/2，V=F/2+2，得到最終存儲的頂點數為n/2，邊數為3n/2。對于一個頂點i（i=1,2,…,3n），在鏈表中查找的平均時間復雜度為o(l)（l為鏈表長度，l=1,2,…,n/2），則去除冗余頂點的時間復雜度為o(n2)。同理，去除冗余邊的時間復雜度為o(n2)。因此，該算法的總的時間復雜度為o(n2)。與其他算法相比，該算法在相同的時間復雜度的情況下，既去除了冗余頂點和邊，又建立了拓撲關系，提高了算法的效率，節省了存儲空間。

2 基于分組思想的分層算法

該算法的基本思想是“整體分組排序，借助分組結果，局部建立基于鏈表的拓撲關系”，即先對所有的三角面片依據其在分層方向的投影值的大小將其分為幾個大組，在此基礎上建立局部拓撲關系，進行分層處理。

2.1 整體分組

假設Z軸為分層切片方向，STL模型在Z軸上的最大值為Zmax，最小值為Zmin。假設將整個模型分為k組，各組的范圍分別為：[Z0,Z1]，[Z1,Z2]…[Zi-1,Zi]…[Zk-1,Zk]，Z0=Zmin，Zk=Zmax。三角面片F在Z軸投影范圍[Fzmin,Fzmax]，Fzmin，Fzmax分別為三角面片在Z軸投影的最小和最大值。如果[Zi-1,Zi]（i=1,2…k）與[Fzmin,Fzmax]有交集，則F屬于第i組。在進行分層時通過分層平面的高度可以直接在對應的組中查找與切平面相交的首個三角面片，減少了三角面片與平面位置關系判斷的次數。

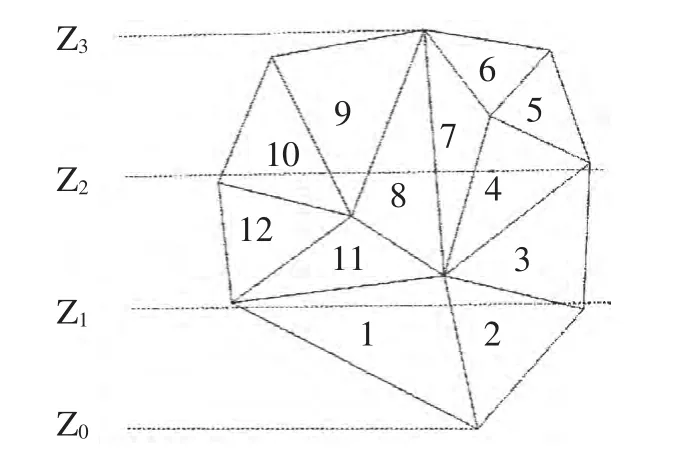
圖4 分組實例

以圖4所示的局部STL模型為例，運用上述分組思想，分組結果如表1所示。

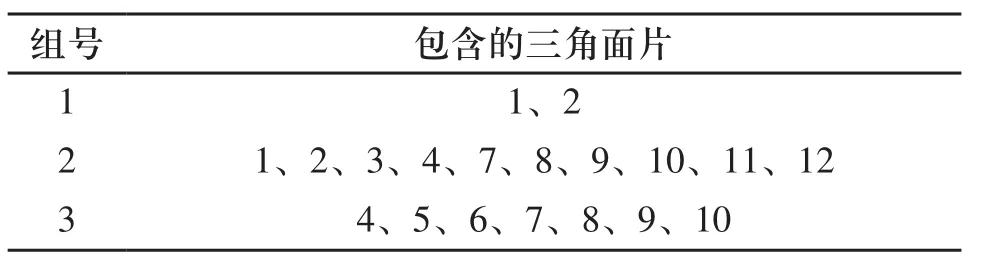
表1 分組結果

2.2 分層切片求取輪廓線

分組之后，采用小節1中拓撲重建算法建立局部拓撲結構，分層求交，獲取輪廓線。先找到一條與當前切平面有交點且未被切過的邊，求出此邊與切平面的交點，保存，并將此邊的位置標志為已切。根據上述拓撲關系找到此邊所屬的三角面片，在三角面片中查找與切平面有交點且未被切過的邊，求其交點，保存。以此類推，則可得到與當前切平面相交的一組首尾相連、封閉的多邊形輪廓線。設Z軸為分層方向，具體分層求交算法如下：

Step1：確定第一個切平面高度h=Zmin（模型在分層方向上的最小值）。

Step2：將elist中所有邊對象的mark置為false，f l ist中所有面對象的mark置為false。

Step3：找到一個與當前切平面相交且未被切過的邊edge0，如果存在則執行下一步，否則跳到step8。

Step4：求邊edge0與切平面的交點，保存，并將該邊的mark置為true。

Step5：根據拓撲關系找到包含該邊的且未被切過的三角面片，將該三角面片的mark置為true，求三角面片另外兩條邊中與當前切平面相交且未被切過的邊，求交點保存，并將該邊的mark置為true。

Step6：重復step5直到回到初始邊edge0，得到與當前切平面相交的一個多邊形輪廓線。

Step7：返回step3，直至求出所有與當前切平面相交的多邊形輪廓線。

Step8：令 h= h+thick (切片厚度)，如果h≤Zmax（模型在分層方向上的最大值），返回step2，否則，退出程序，切片完成。

整體分組、局部建立拓撲關系可以有效的降低STL建立拓撲關系的算法復雜度。由于建立拓撲關系時的算法復雜度與面片個數的平方成正比，假設一個STL文件中包含n個三角面片，如果對整個模型建立拓撲關系算法復雜度為o（n2）；如果將整個STL文件按分層方向分為k（k

理論上，k越大，即組數越多，算法復雜度越小，但是k過大，組之間重疊的三角面片數量過多，重疊的面片在不同的組之間重復建立拓撲關系增加了算法的復雜度。以圖5所示軸套為例，三角面片的數目為8537個，分組數分別取1、10、20、30、40、50，分層厚度為2mm，分組切片時間開銷（每個分層組數重復仿真20次，求取時間的平均值）如表2所示。

通過對表2進行分析，可以發現當分組數目逐漸增大時，分層算法的時間開銷逐漸減少；但是當分組數目大于20時，時間開銷開始增加。由此可見，分組組數并不是越大越好。因此，對于不同的零件和三角面片數量要選擇合適的分組組數。

3 模型仿真與對比

在軟硬件環境相同的情況下，三種不同切片算法的對比如表3所示，其中m為三角面片的個數，h為分層厚度，T1為基于拓撲信息的切片算法所用時間，T2為基于三角形幾何特征的切片算法所用時間，T3為本文算法所用時間（每種算法重復仿真20次，求取時間的平均值），g為本文算法對三角面片進行分組所得的組數。由表1可以看出，與其他2種算法相比，隨著模型三角形面片個數的增加，本文算法的效率逐漸提高。

4 結論

該算法綜合考慮了現有切片算法的特點，提出了分組的思想降低了建立拓撲關系的算法復雜度，并同時提出了基于鏈表的拓撲重建算法，在建立拓撲關系的同時去除了冗余數據，降低了算法空間開銷。最后通過實例仿真，證明了算法的可行性和高效性。根據三角面片數量以及零件形狀精確的確定最優的分組數量以使算法復雜度得到進一步的降低是未來研究的重點。

表3 不同切片算法對比

[1]顏永年,張偉,盧清萍,王剛,刁慶軍,時曉明.基于離散/堆積成型概念的RPM原理和發展[J].中國機械工程,1994,5(4):64-66.

[2]韓光超,張海鷗,王桂蘭.面向金屬模具快速制造的機器人成型加工系統[J].機器人,2006,28(5):515-518.

[3]劉光富,李愛平,王東立.三維實體零件分層處理軟件的研究與開發 [J].制造業自動化,2004,26(11): 21-24.

[4]王素,劉恒,朱心雄.STL模型的分層鄰接排序快速切片算法[J].計算機輔助設計與圖形學學報,2011,26(4):4-6.

[5]謝存禧,李仲陽,成曉陽.STL文件毗鄰關系的建立與切片算法研究[J].華南理工大學學報(自然科學版),2000,28(3):33-38.

[6]李仲陽,謝存禧,楊家紅.基于STL文件的快速成型分層算法與毗鄰拓撲信息的快速提取[J].計算機工程與應用,2002,38(7):32-35,79.

[7]趙吉賓,劉偉軍.快速成形技術中基于STL模型的分層算法研究[J].應用基礎與工程科學學報,2008,16(2):224-233.

[8]CHOI S H,KWOK K T.A tolerant slicing algorithm for layered manufacturing[J].Rapid Prototyping Journal,2002,8(3):161-79.

[9]趙保軍,汪蘇,陳五一.STL數據模型的快速切片算法 [J].北京航空航天大學學報,2004,30(4):329-333.

[10]胡德洲,李占利,李滌塵,et al.基于STL模型幾何特征分類的快速分層處理算法研究[J].西安交通大學學報,2000,34(1):37-40,45.

[11]李占利,梁棟,李滌塵,et al.基于信息繼承的快速分層處理算法研究[J].西安交通大學學報,2002,36(1):43-46.

[12]趙吉賓,劉偉軍.快速成型技術中分層算法的研究與進展[J].計算機集成制造系統,2009,15(2): 2-21.

[13]SAHNI S.數據結構,算法與應用 [M].北京:機械工業出版社.2000.