永磁同步直線電機最大效率控制研究
崔皆凡 潘龍玉
(沈陽工業大學電氣工程學院,沈陽 110870)
永磁同步直線電機最大效率控制研究
崔皆凡 潘龍玉
(沈陽工業大學電氣工程學院,沈陽 110870)
針對電動機驅動系統效率問題,對永磁同步直線電機驅動系統最大效率控制進行了分析和研究。從分析永磁直線電機的電機損耗模型入手,建立考慮逆變器損耗時的系統損耗模型。利用拉格朗日優化算法,推導出永磁同步直線電機在矢量控制下穩態運行時效率最高的控制條件。基于損耗模型設計效率模糊控制器,使系統具有更好的魯棒性。通過Matlab/simulink實驗仿真驗證所建立的模型在穩態下有較高的準確度,同時保證輸出功率不變,實現最大效率控制。
永磁同步直線電機;損耗模型;最大效率;矢量控制
隨著永磁材料的發展,永磁同步直線電機在諸多領域中日益得到廣泛應用。但在實際應用中,由于電機產品容量的不連續性等因素,使得大部分的PMSLM 處于輕載運行狀態,效率沒有達到最大。因此,研究PMSLM的最大效率問題顯得十分必要。
最大效率控制通常分為搜索控制法和損耗模型控制法[1]。對于搜索控制法,它是一種純數學方法,效率尋優過程與電機內部參數無關。損耗模型控制法是建立電機的損耗模型,根據當前狀態、控制要求推導效率最大時的推力電流與當前負載和速度的關系,從而實現最大效率控制。文獻[2]采用了最大轉矩電流比控制方法來提高永磁電機效率,此方法提高了系統的動態性能,但是電機損耗卻沒有明顯的減少;文獻[3]研究永磁同步電機的矢量控制原理的仿真模型,但該文獻沒有考慮到系統中逆變器的損耗。當前諸多研究存在著一定的局限性。針對以上這些,本文根據給定電機運行狀態,以系統效率最大為目標,對PMSLM及其驅動系統的損耗進行綜合分析,進行精確建模,實現最大效率控制。根據損耗模型特點,設計了效率模糊控制器,提高了系統的魯棒性與系統響應的快速性。
1 系統損耗分析
PMSLM 驅動系統包括逆變器、檢測電路、控制電路和電機本身。由于傳感器和控制電路的損耗很小,所以主要考慮電機和逆變器的損耗。
1.1 電機損耗分析
考慮PMSLM系統效率,為了保證建立的損耗模型考慮的更全面,本文針對電機損耗Ploss1以整體考慮,通過測得電機的輸入Pin和輸出Pout,來進行建立電機損耗模型:

1.2 逆變器損耗分析
逆變器的損耗主要包括電力電子器件的驅動損耗以及電力電子器件本身的損耗。目前變頻調速系統的電力電子器件以 IGBT為主,其驅動損耗非常小予以忽略。通過文獻[4]綜合分析對于一特定的逆變器而言,損耗主要由其集電極電流所決定,逆變器損耗近似為定子電流函數:

式中,k1、k2由對應的開關管IGBT和二極管各參量所決定的常系數,is為定子相電流。考慮逆變器損耗后變頻驅動永磁同步直線電機系統損耗Ploss可表示為

2 PMSLM系統損耗模型
損耗模型法實現最大效率控制需要建立在特定應用場合下的電機損耗模型,該模型要求簡單、準確并且實用。dq軸是以同步電角速度在空間旋轉的正交軸系,PMSLM在dq坐標軸上的電壓表示為


在電機等效電路中,通常將鐵耗等效成純電阻,對于PMSLM主要考慮初級鐵耗。當考慮鐵耗時,將PMSLM中的永磁體等效一個勵磁線圈,并且與初級線圈具有相同的有效匝數,等效電流為 if,可產生與永磁體相同的基波勵磁磁場,所以可得到如下關系式:

由于初級磁鏈的幅值是受控的,且 if基本保持不變,所以pψmd、pψmd很小,為簡化數學模型可以忽略不計。將式(17)用等效電路表示出來,根據考慮鐵耗時的等效電路圖有


矢量控制中當采用id=0的控制策略時,可見損耗是關于交軸電流幅值 iq的函數。通過利用拉格朗日優化方法求得效率最大時的條件表達式為

3 基于模糊控制技術的PMSLM最大效率控制方法的研究
基于損耗模型的PMSLM最大效率控制方法雖然實時性好,但該方法容易受電機參數影響,控制效果取決于損耗模型的準確程度[8]。為了提高系統的魯棒性與快速性,本文設計了一種新型的PMSLM效率模糊控制器:根據逆變器直流側輸入功率的偏差情況來決定是否將直流側輸入功率偏差變化率作為第三輸入變量;搜索初值根據所建系統損耗模型進行選取;在線實時進行計算比例因子,解決控制不足或死區問題。
本文設計的效率模糊控制器包涵結構如圖1所示。

圖1 效率模糊控制器組成
輸入功率計算環節的任務是采樣直流側輸入功率,可由檢測到的直流測電壓和電流計算得到。
比例因子計算環節的任務是實時在線計算輸入輸出變量的比例因子,將輸入變量轉換成標么值的形式,即將輸入變量的基本論域標么化成[-1, 1],這樣同一個模糊規則就可以較好地適用于不同功率等級的永磁同步直線電機或同一永磁同步直線電機的不同工作狀況,標么化后的輸入變量將被用于進行模糊推理。
模糊控制環節是整個效率模糊控制器的核心,其輸入變量分別為直流側輸入功率偏差ΔP、輸入功率偏差變化率ΔP˙和上次電樞電流變化量 iq( k 1)Δ˙- ,模糊控制器的輸出則是當前電樞電流變化量其中, ΔP˙要視ΔP大小決定是否作為輸入變量,當ΔP較大時,以減小偏差為主,此時ΔP˙不起作用,系統為二維控制結構;而ΔP當較小時,為了使控制更加精細,以減小系統超調,同時加快搜索速度,此時將ΔP˙作為第三輸入變量,系統變為三維控制結構。
效率模糊控制器的工作流程如下。

圖2 效率模糊控制器的工作流程圖
4 系統最大效率控制仿真研究
根據當前負載和速度,建立驅動系統的損耗模型,從而保證系統時時刻刻處于最大效率控制。本文采用的電機模型參數具體如下:額定電壓 UN=380V,額定頻率 fN=50Hz,額定功率 PN=3kW,磁極對數 PN=4,鐵耗等效電阻 R=2.98Ω,極距τ=0.016M,永磁體ψf=0.4WB,每相繞組阻值 R=2.98Ω,dq軸電感Ld=Lq=0.0085H,轉速v=3m/s,由逆變器開關器件決定的互相關系數k1=0.12、k2=2.5。
根據仿真實驗,有以下常規矢量控制與最大效率控制下矢量控制數據對比,見圖3至圖5。

圖3 推力波形

圖4 速度波形
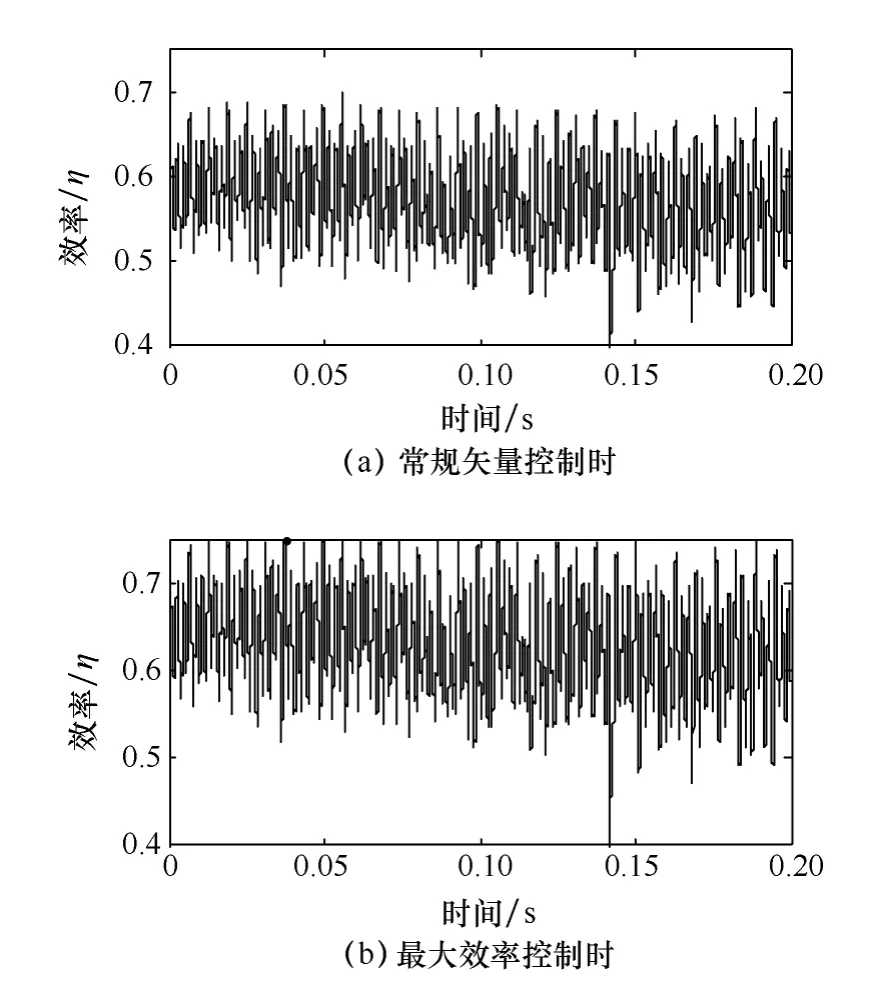
圖5 效率波形
5 結論
本文通過對PMSLM系統最大效率控制的分析研究可以得出以下結論。
1)相比常規矢量控制,穩態時最大效率控制的推力波動更小了,常規矢量控制的波動范圍是80~120N,最大效率控制時推力波動范圍是90~110N,對比波幅縮減了10%;速度跟隨預期效果更準確了,常規矢量控制時速度均值為2.53m/s,最大效率控制時速度均值為2.75m/s,相比控制更精確了;在保持輸出功率不變的前提下,傳統矢量控制的效率為59.8%,最大效率控制時系統效率為65.7%,系統效率由提高了5.9%。
2)相比常規矢量控制,最大效率控制在穩態給定速度和推力的情況下,能夠使系統更快達到最大效率工作狀態,并且最大效率控制的運行條件是已經計算出來的,與人為經驗因素無關,便于應用。
[1] 徐占國. 電動車用感應電機矢量控制系統的研究[D].大連理工大學, 2010: 22-23.
[2] 郭慶鼎,陳啟飛,劉春芳. 永磁同步電機效率優化的最大轉矩電流比控制方法[J]. 沈陽工業大學學報,2008, 30(1): 1-5.
[3] 丁文,高林,梁得亮,等. 永磁同步電機矢量控制系統的建模與仿真[J]. 微電機, 2010, 43(12): 66-71.
[4] 劉建強. 直線電機軌道交通牽引傳動統研究[D]. 北京交通大學, 2008: 95-97.
[5] 王成元,夏加寬,孫宜標. 現代電機制技術[M]. 北京:機械工業出版社, 2008: 128-129.
[6] 張穎. 永磁同步直線電機磁阻力分析控制策略研究[D]. 華中科技大學, 2008: 59-60.
[7] 劉曉. 空心式永磁直線電機伺服電機其驅動控制系統研究[D]. 浙江大學, 2008: 107-110.
Loss Model of the Permanent Magnet Synchronous Linear Motor under Efficiency Maximization
Cui Jiefan Pan Longyu
(School of Electrical Engineering, Shenyang University of Technology, Shenyang 110870)
The efficiency maximization control condition for PMSLM vector control is studied and analyzed for the problem of efficiency of the motor drive system. The system loss model considering the inverter loss is established through analysis of the loss model of the permanent magnet synchronous linear motor (PMSLM). The efficiency maximization control condition for PMSLM vector control drive at steady state condition is derived using lagrange theorem. To make the system has better robustness,the fuzzy controller of efficiency based on the system loss model is designed. The experimental results show that the proposed model is accurate at steady state by Matlab/simulink.While keeping the output-power constantly, the purpose that rapidly reached the efficiency maximization can be achieved.
PMSLM; loss model; efficiency maximization; vector control
崔皆凡(1963-)女,沈陽工業大學電氣工程學院,教授,博士,主要從事特種電機及其控制的研究。

