海洋模式中垂直混合參數化方案介紹

汪雷，王彰貴，凌鐵軍，左金清

（1.北京大學物理學院，北京100871；2.國家海洋環境預報中心國家海洋局海洋災害預報技術研究重點實驗室，北京100081；3.中國氣象局國家氣候中心中國氣象局氣候研究開放實驗室，北京100081）

海洋模式中垂直混合參數化方案介紹

汪雷1,2，王彰貴2，凌鐵軍2，左金清3

（1.北京大學物理學院，北京100871；2.國家海洋環境預報中心國家海洋局海洋災害預報技術研究重點實驗室，北京100081；3.中國氣象局國家氣候中心中國氣象局氣候研究開放實驗室，北京100081）

介紹了海洋垂直混合過程參數化方案的發展，以及不同參數化方案在海洋模式中的應用情況。首先，介紹不同垂直混合參數化方案的物理問題、理論依據、數學表達和特征，并對不同參數化方案進行了比較。其次，針對中尺度渦、亞中尺度渦以及波浪、潮流混合參數化的最新研究進展進行了總結并對垂直混合參數化的未來發展提出了一些建議。

湍流閉合方案；中尺度渦混合；亞中尺度渦混合；波浪混合；潮流混合

1 引言

地球流體原始方程組通常描述了一定時空范圍平均的流體運動行為。由于受到計算資源的限制，在數值計算中往往需要在更大的時空尺度上求解流體運動方程。更小尺度運動的效應，常以湍流通量散度形式出現[1]，它們需要利用大尺度變量來參數化以閉合方程，這些過程常被稱作次網格尺度物理過程。

海表混合層是海洋上層中直接與上覆大氣、海冰相互作用的部分。一個完備的海表混合層參數化[2]，必須模擬海風攪拌驅動的混合、不穩定浮力強迫、流切變不穩定、湍流平流、非局地混合，例如密集羽流滲入層流、重力內波破碎等物理過程。海洋內部溫鹽等屬性沿位密面的傳輸主要通過大尺度洋流和中尺度渦來實現，而海洋內部跨密度混合發生在重力內波破碎區域[3]，大部分波能量來源于海底反射的潮流、小尺度地形下重力波產生和輻射對地轉運動的耗散、以及斜壓不穩定的失穩。隨著觀測增多、模式發展和分辨率的提高，中尺度渦、亞中尺度渦以及波浪、潮流等過程對海洋混合的影響受到越來越多的關注。圖1給出了海洋中小尺度混合過程的示意圖。

海洋垂直混合是海洋混合中的重要部分，受到模式分辨率的限制，其在模式中需要進行參數化。海洋垂直混合參數化方案，根據混合系數的選取可分為：常混合系數、依賴Richardson數的方案和湍流動能模型等[1]。常混合系數方案，動量垂直粘性和示蹤物垂直擴散系數在整個海洋設定為常數。由Richardson數決定的混合方案，利用觀測資料尋找垂直湍流活動和大尺度海洋結構之間的聯系，通過模型診斷出垂直混合系數與大尺度變量之間的關系。湍流閉合模型，則是一種基于湍流動能診斷方程和湍流特征長度閉合假設的模型。隨著觀測的增多和理論的發展，許多小尺度物理過程得到了更精確的刻畫。

范植松[4]回顧了大洋內部、淺海內部混合的主要過程和一些參數化方法。近十年來，隨著海洋模式的發展，國內外涌現出了一些新的海洋垂直混合參數化方案。本文將介紹影響重大的海洋垂直混合參數化方案、以及該領域最新的進展，并進行系統的總結與展望。

2 海洋垂直混合參數化方案

海洋模式旨在求解大尺度速度和溫鹽度的運動學方程，其中，動量、溫鹽通量是由速度、溫鹽擾動量的非線性相互作用所引起的。在局地湍流模型中，動量、溫鹽通量常表示為大尺度變量梯度的函數。模式分辨率通常大于切變不穩定、內波破碎等垂向湍流發生的主要源匯尺度，湍流運動一般未能顯式求解，而是需要對其進行參數化處理。海洋上層的垂直混合過程是大氣和海洋之間熱量、水、動量交換的重要方式，下面我們將介紹一些具有代表性的垂直混合參數化方案。

2.1 KT67混合層模型(The Kraus-Turner mixed layer model)

研究對象：Kraus和Turner[5]考察了海表過程如輻射穿透、海表冷卻和風攪拌所引起的層結過程。在盛夏，輻射穿透引起的對流混合與風攪拌作用具有相同的量級；在冬季，混合層厚度和穩定性主要由海表冷卻控制，輻射穿透或風攪拌的作用相對較小。

理論依據：假定影響水柱的熱量和機械能不受水平速度、平流或旋轉的顯著影響，而在海表附近向下穿透，Turner和Kraus[6]建立了一個簡單的季節溫躍層模型。在熱量給定時，所有攪拌動能用于改變系統的位能，充分混合后得到表層混合厚度和溫度。

表達形式：混合層是垂直均質水層，在假定外源、匯平衡后略去時間傾向項，得到湍流動能診斷方程，求解水層厚度。通過熱量平衡以及動能平衡方程得到水層厚度[5]：

式中，k，ε，SR，IR，l分別與風輸入動能、耗散、太陽輻射、紅外輻射和長度尺度有關。

混合層底的厚度是模式預報量。在密度坐標系模式中，KT67混合層模式的混合層底與模式垂直坐標吻合，但卷出過程很難處理。

在混合坐標海洋模式如HYCOM[7]中，KT67混合層模式兼容的困難之處在于，需要記錄混合層底的浮力變化以近似混合層夾卷對湍動能平衡的貢獻，和熱力、動力變量不連續以計算混合層夾卷對其影響。完整KT67方案，設計unmixing方案以減少混合層和海洋內部屬性的數值交換。由于unmixing方案十分復雜，簡化KT67方案通過松弛混合層底為預報量這一條件，在計算效率提高和數值誤差增長之間權衡。

特征：KT67模型[5]僅僅控制表面混合層，使用時需同時加入考慮內部跨密度混合算法。HYCOM[8]提供了該參數化方案選項。

2.2 PWP86動力不穩定模型(Price-Weller-Pinkel dynamical instability model)

研究對象：海洋上層的熱含量存在著眾所周知的日循環，午后的溫度、速度廓線表現出海表混合、分層剪切的上下兩層結構。在海表加熱和風應力已知時，預報海洋日循環的關鍵在于熱量“陷阱”的確定。Price等[9]發展了一個對加熱和風混合響應的上層海洋簡單模式，以模擬日循環。

理論依據：在僅僅使用混合層夾卷時，整體混合層模式可給出合理的表面強迫，但對過渡層的模擬存在突變和偏淺的問題。在僅僅使用梯度混合時，模式對表面強迫的模擬也相對合理，只是無法模擬風驅動的海表混合層，加入自由對流過程后可得到改善。通過構造海表混合層，并且考慮混合層下的層流混合，可得到相當真實的廓線結構[9-10]。

表達形式：混合由三步完成：

（1）自由對流。海表熱量損失出現靜力不穩定時(?zρ≥0)，發生自由對流，對流混合至對流深度（日循環的典型值小于1 m）；

（2）整體混合層夾卷。當整體Richardson數(Rib)小于臨界值（0.65）時，混合層夾卷相鄰下層，在新形成的混合層中使所有的變量均質，其中

（3）相鄰層結垂直切變不穩定混合。若Richardson數(Ri)小于臨界值（0.25）時，界面上下層混合，其中，Brunt-V?is?l?頻率，ρ為位密。在日循環中，后兩種混合在垂直混合過程中占優勢，由于Richardson數中出現的速度完全是由風驅動的，從這種意義上來說，可視為風-混合過程。

特征：PWP86方案[9]丟失了混合層特征，如對數廓線和非局地輸送；在對流穩定條件下，該方案無法描述在混合層以下層結區由對流引起的額外夾帶。PWP86方案提供了表面混合層以下的切變不穩定混合，未給出內波破碎等引起的背景混合。HYCOM[8]使用PWP86方案時，同時啟動顯式跨密度混合算法。

2.3 BL79方案(Bryan-Lewis water mass model)

研究對象：考察海洋環流在地球熱平衡中的作用時發現，溫躍層厚度對次網格尺度運動的參數化方案十分敏感，其中溫躍層的平均厚度與全球有效位能成正比[11]。

理論依據：在地轉條件下，即使閉合參數不同，有效位能和總動能也保持一個幾乎恒定的比例。浮力強迫做功使動能轉化為位能，浮力做功引起能量傳輸的方向取決于能量庫的耗竭情況，即耗散、風做功供給和非均勻加熱的差異[12]。溫躍層厚度與參數變化之間有明確的格局，當參數改變使得風做功增加或者耗散減小時，海洋環流的總能量增加，這意味著密度層結更大的偏移和模式中更深的溫躍層。

表達形式：溫鹽控制方程為：

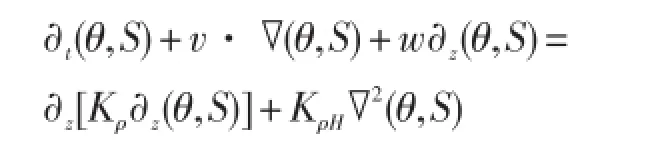
式中，水平粘性系數KmH和垂直粘性系數Km取為常數。水平擴散系數KρH是垂直坐標的函數KρH(z)=KρHB+(KρHS-KρHB)e-0．002z。垂直混合系數是穩定度的函數，不穩定時，系數無限大，不穩定水柱溫鹽徹底混合；穩定時取為垂直坐標的簡單函數。垂直擴散系數Kρ在溫躍層最小且隨深度增加而增大，其計算方程考慮了風攪拌對上層海洋的作用：

特征：在海洋環流數值模式尤其是氣候模式中，通常采用BL79方案[11]來確定背景垂直湍擴散系數。該方案給出的垂直湍擴散系數只是深度z的函數。MOM[13]等加載了BL79方案。

2.4 PP81混合方案(Pacanowski-Philander mixing scheme)

研究對象：海表混合過程非常重要，KT67模型[5]考慮了風攪拌和跨混合層的夾帶作用，但是忽略了海洋對風場變化的動力響應，故KT67模型在局地通量占主的區域效果不錯。而在風場再分布效果大于局地作用的熱帶地區，KT67模型表現不佳。在熱帶海洋的上層，表面通量和對風場變化的動力響應都是重要的。

理論依據：觀測表明，混合過程受到平均流剪切的強烈影響[14-15]。通過經驗研究，Jones等人[16]給出了黏性/擴散系數與Richardson數的關系。PP81混合方案[17]主要應用在熱帶海洋，擴散系數依賴于Richardson數。由于該方案能夠較合理地描述強垂直切變與黏性之間的關系，它可以更好地模擬赤道溫躍層和赤道潛流。

表達形式：垂直擴散系數和粘性系數是Richardson數(Ri)的函數。式中，垂直粘性系數Km為：；垂直擴散系數Kρ為：背景值Kmb、Kρb由運行時間決定。在POP中，α=5，n=2。

特征：海洋混合過程極其復雜，PP81混合方案[17]只是簡單地把垂直混合系數設為Richardson數的函數，而忽略了其它的混合過程，造成該方案在中高緯度的模擬結果不佳。由于湍流動能耗散率與Richardson數的關系隨深度變化，PP81方案依賴于Richardson數的簡單混合參數化方法并非對所有深度有效。采用該方案的模式有LICOM[18]、MOM[13]、NEMO[1]、POP[19]等。

2.5MY82湍流閉合方案(Mellor-Yamada Turbulence Closure Model)

研究對象：湍流粘性或混合長假說對二維湍流邊界層有可觀的預測能力。無壓力梯度、熱傳輸時，平均速度場閉合模型采用常數參數的平坦湍流層，無法預測層結效應。平均湍流場閉合模型由平均湍流能量模型和平均雷諾應力(MRS)模型組成時，雖然成功用于中性層，但是對于分層流MRS的計算量驚人。

理論依據：將湍流理論擴展到層結流體，Mellor[20]建立了湍流閉合模型。為了實現準確性和計算速度的優化，Mellor和Yamada[21]利用觀測對湍流模型進行了簡化。從四階到二階模型，求解的偏微分方程數量由十個降到兩個，而結果十分相似。為便于其在三維大氣和海洋模型中的應用，Mellor和Yamada[22]對三階模型簡化得到2.5層模型。

表達形式：溫度擴散方程可寫為：

式中，粘性系數Km和擴散系數Kρ取決于湍流速度尺度q、特征長度l以及反映層結的Richardson數Ri[22]：

湍動能k和預報量kl，由下列方程控制：

方程右端代表局地過程的作用。左側第二至四項分別為水平平流、水平擴散、坐標轉換時跨坐標引起的通量。溫、鹽項的局地作用表現為垂直擴散和海表強迫。湍動能和預報量的局地作用表現為邊界層強迫、垂直擴散以及垂直切變產生、與位能的相互轉化以及耗散。Sρ，Sm與Ri的有關：

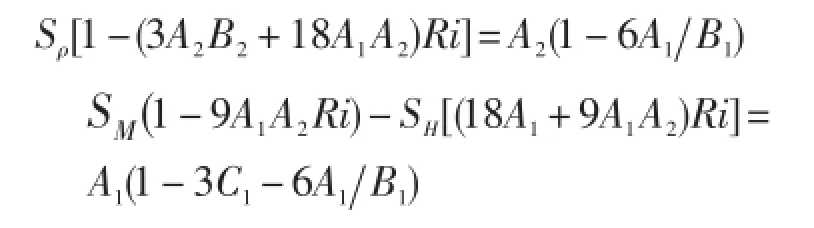
特征：MY82方案[20-22]產生從海表到海底的混合，弱混合發生在海洋內部，強混合產生在海表邊界層，增強混合在洋底。該方案對混合層動力過程的模擬較好，但混合層厚度可能偏淺[23]，在對流夾帶偏弱、穩定密度梯度情況下混合偏小[24]。MY82方案的湍動能和預報量，在POM[25]中是垂直交界面變量，而在HYCOM[8]中是層變量。

2.6 GGL90湍流閉合方案(Gaspar-Grégoris-Lefevre TKE Turbulent Closure Scheme)

研究對象：對于那些垂直擴散系數為常系數或依賴Richardson數的簡單參數化方案，上混合層模擬往往較差。簡單整體模型如KT67[6]計算高效，但是僅適用于邊界層。復雜的湍流閉合方案如MY82[21]，提供了更加真實的垂直湍流混合，但在湍流主長度尺度的確定上存在不足。

理論依據：GGL90湍流閉合方案[26]是一種基于湍流動能診斷方程和湍流長度尺度閉合假設的參數化方案。Bougeault和Lacarrère[27]最早提出了簡單、物理意義清晰的大氣湍流閉合模型，Gaspar等[26]將其應用到海洋模式中，Madec等[28]對混合長度尺度的公式進行了改進。

表達形式：湍流動能的時間演變是垂直切變制造、層結破壞、垂直擴散和Kolmogorov耗散共同作用的結果[26]：

式中，海表湍動能由風應力場確定，當考慮表面波破碎時，使用較大的值。假設底層湍動能為緊鄰上層湍動能的值。其中，垂直渦粘性和渦擴散系數分別為：

lε和lk分別為粘性、混合長度尺度，Prandtl數(Prt)依賴于局地Richardson數。簡化的湍流長度尺度：，以到海表lu、海底ld、或局地垂直尺度因子為界，僅適用于層結穩定區域。針對局地層結不穩定，考慮長度尺度的垂直梯度項[28]：，即長度尺度的垂直變化不大于深度變化。

通過修正表面長度尺度和湍動能的數值以及海氣拖曳系數來參數化表面波破碎能量效應[29-30]。 GGL90上邊界條件為[29]：αCB是取決于“波齡”的常數。湍流長度尺度的上邊界條件：，VC是von Karman常數，CC是Charnock常數。

特征:GGL90方案[26]指定了兩種不同的特征尺度來分別表示混合和耗散，由于它們與所有深度的湍流長度相關，所以得到的混合參數化并不限于上邊界層，而是可以應用在海洋整層。MITGCM[31]、NEMO[1]等模式采用了該參數化方案。

2.7 GISS01混合層模式(Goddard Institute for Space Studies)

研究對象：海洋混合過程的模擬通常采用單點湍流閉合模型，特別是MY82方案[22]開創了1980年代最先進的湍流模型。該方案使用了較小的臨界Richardson數，且假定湍流不受旋轉影響。隨著湍流模型的發展，一些關鍵物理過程的模擬，如臨界Richardson數取值、非局地分層和剪切、旋轉、混合層下的混合等，都需要得到進一步的提高[32]。

理論依據：GISS01混合層模式根據實驗觀測來調整臨界Richardson數（約為1），并通過求解動力系統三階方程而得到包含分層和剪切作用的表達式。在混合層下的開洋面上考慮內波破碎等，地形附近則考慮潮耗散或地熱加熱作用。提出了雷諾應力模式的熱、動量擴散系數表達式[32]，并對雙擴散過程[33]進行了完善。

表達形式：擴散系數Kρ(rρ,N,Ri,ε)取決于密度比rρ、Brunt-V?is?l?頻率N、Richardson數Ri和動能耗散率ε，其中下標ρ=(m,h,s)分別代表動量、熱量和鹽度，

密度比和Brunt-V?is?l?頻率由海洋環流模式的大尺度場計算得到。剪切作用由Richardson數表征，混合層內主要為風驅動的大尺度剪切，混合層之下則是小尺度剪切如內波為主。耗散率表示混合相關的物理過程，混合層內主要為風攪拌作用；在混合層下的開洋面上考慮內波破碎等，地形附近則考慮潮耗散或地熱加熱作用。GISS01方案適用于雙穩定、雙不穩定、鹽指和對流擴散情況：

雙穩定(?zT＞0,?zS＜0,rρ＜0,RiT＞0)

雙不穩定(?zT＜0,?zS＞0,rρ＞0,RiT＜0)

鹽指(?zT＞0,?zS＞0,rρ＞0,RiT＞0)

擴散對流(?zT＜0,?zS＜0,rρ＞0,RiT＞0)

特征：GISS01方案[32-33]適用于混合層及其以下的垂直混合參數化。該方案首先計算壓力網格點上的粘性、擴散系數，隨后使用隱式方案求解垂直擴散方程，并將粘性廓線水平插值到速度網格點，最后求解動量的垂直擴散方程。GISS01方案未對非局地效應進行參數化。HYCOM[8]加載了該參數化方案。

2.8 GLS03湍流閉合方案(Generic Length Scale scheme)

研究對象：海洋模式中雷諾-應力模型的應用在湍流長度尺度的選擇上存在爭議。所有雷諾-應力和兩階-方程模型都采用了經典串級模型：在物理上，使用(l，ε)中某變量并無客觀優勢，而在數學和計算上，模式性質受到長度尺度變量的很大影響。

理論依據：GLS03湍流閉合方案[34-35]包含兩個預測方程：湍動能方程k和通用尺度ψ方程。通過適當的變換，GLS03方案可以復原一系列著名的湍流閉合方案，如MY82的k-kl方案[22]、Rodi的k-ε方案[36]和Wilcox的k-ω方案[37]等。

表達形式：湍動能由湍流傳輸Tk、切變產生GS、浮力制造GB和耗散項ε確定：

通用尺度lψ與湍動能和耗散相關lψ=~lψ(k,ε)，方程可寫為：

式中，Tψ為傳輸項，cψ1、cψ1和cψ1是模式常數。進一步假定lψ依賴于k和ε的乘積：，通過適當變換p、m和n的值，通用尺度方程可復原一系列著名的模型（見表1）。

表1 通用尺度中定義的p、n和m及其與著名二階方程模型的關系[34]

在一定條件下，GLS03方程組可以化為[1]：

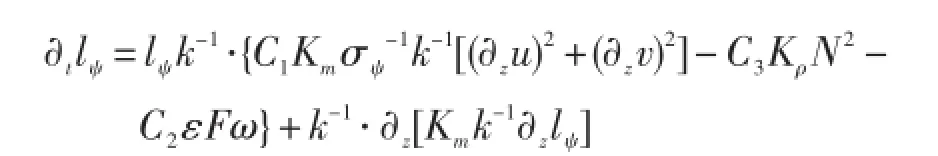
特征：GLS03方案[34-35]既可以用來分析已有模式，本身又可作為廣義模式方程。對于制造等于耗散的傳統標準流動情況，GLS03方案與傳統模式表現相當。但對于無切變情形，耗散由湍流傳輸平衡的情況，此時除Wilcox的k-ω方案[37]外模擬效果都不好。傳統模式對邊界附近廓線的模擬存在困難。另外，GLS03方案解析解指出，模式參數間相互依賴很強。當合理使用這些參數時，模式在均質層結、切變流中表現良好。NEMO[1]等模式采用了該參數化方案。

2.9 KPP94參數化(K-Profile Parameterization)

研究對象：海洋垂直混合過程可分為海表邊界層和海洋內部兩種截然不同的混合型。通常使用的混合方案未考慮某些潛在重要的邊界層物理過程，需要發展新的參數化方案代表這些物理過程。

理論依據：在海表邊界層，KPP94方案對風驅動混合、表面浮力通量和對流不穩定進行參數化。在海表強迫下，邊界層混合增強，這使得邊界層屬性滲透到溫躍層。海洋內部混合由切變不穩定、背景內波破碎和雙擴散控制。另外，該方案還對溫、鹽非局地混合作用進行了參數化，允許逆梯度通量的發展。

表達形式：KPP94方案[38-39]為半隱式，需要多步迭代過程。首先，在模式界面和網格上計算內部混合系數。其次，診斷出網格上的邊界層深度。第三，計算網格上的邊界層混合系數，代替初始值。最終得到網格上的平均系數。

海表通量：初始海表熱力、動量通量在上層設為均勻分布[8]。

海表邊界層厚度由整體Richardson數(Rib)確定。

垂直混合：通過水平平流、擴散、動量和通量方程得到每個網格點變量值，將垂直擴散視為海表、底邊界上零通量的純一維問題求解。

特征：非局地KPP 94方案[38-39]是非剛蓋混合層模型，統一了垂直混合中的多種未解析過程[31]，以處理海洋邊界層、海洋內部的不同混合過程。KPP94方案有效地刻畫了從海洋邊界層到海洋內部混合系數減小的特點，可以應用在較粗網格和不平坦地形情況[8]，在HYCOM[8]、MITGCM[31]、MOM[13]、NEMO[1]、POP[19]等模式中使用。

2.10 GM90中尺度渦參數化(Gent-McWilliams Parameterization)

研究對象：中尺度渦是渦旋場中最有活力的部分，支配著物質屬性的等密度面混合。前人提出的渦擴散通量是沿等密度面的方向，而這不滿足平均密度平衡。GM90方案[40]針對非渦分辨海洋環流模式，將次網格中尺度渦混合參數化，以描述中尺度渦對于大尺度位溫、鹽度及其它示蹤物的影響。

理論依據：絕熱和風驅動環流的精細數值解表明，平均速度導致的大尺度密度通量散度由中尺度渦誘發的密度通量散度平衡。GM90方案利用準絕熱參數化的構想，在粗分辨率模式中保持平均示蹤物濃度在等密度面上守恒。等密度層厚度沿等密度面進行混合，對示蹤物附加平流和擴散項來實現中尺度渦對示蹤物傳輸的參數化。將大尺度速度與渦誘發速度之和視為“有效速度”，得出與絕熱模型相似的解[41]。

表達形式：示蹤物傳輸方程為[19]：式中，中尺度渦誘發的推注速度：方程右側第一項采用等中性擴散算子[42]：R(φ)=?3(K·?3φ)，K代表沿等密度面擴散的對稱張量。在POP模式中，將推注速度寫為偏斜通量形式[43]：，B代表反對稱張量。

傳輸方程可以重新寫為：

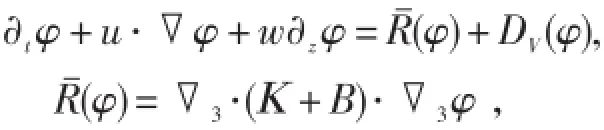
新公式對中性坡度的描述避免了非線性不穩定的激發。

在MITGCM中，渦參數化方案調用GM90方案前，首先使用Redi渦參數化方案[42]，利用沿局地等熵面的擴散算子實現示蹤物屬性沿等熵面的混合。

特征：GM90方案[40]要求將背景擴散項中的水平擴散部分去掉，這是因為它有可能產生不適當的穿過等位密度面的擴散。對于次網格尺度的物理過程，GM90方案給定的側向渦旋系數對大尺度度特征實際變化的反映并不理想，且未考慮跨密度混合。使用該方案的有LICOM[18]、MITGCM[31]、MOM[13]、NEMO[1]、POP[19]。

2.11 FKFH08亞中尺度渦參數化(Fox-Kemper-Ferrari-Hallberg restratification effects by submesoscale eddies)

研究對象：典型的海洋層化和切變允許兩種斜壓不穩定：貫穿整個深度的深厚中尺度不穩定，以及限于弱層結海表混合層的淺薄亞中尺度不穩定[44]。淺混合層不穩定是非地轉斜壓不穩定，以其快速增長率、小尺度區別于深厚中尺度不穩定，且前者在強混合事件后上層海洋的再層化中發揮重要作用。

理論依據：對于FKFH08方案[45-46]，海洋混合層亞中尺度渦再層化效應發生的時間尺度遠小于由中性物理參數化的中尺度渦。有限振幅斜壓不穩定驅動了混合層的再層化，等密度面發生由垂直向水平的傾斜。參數化過程引入了翻轉流函數，它正比于水平密度梯度、混合層深度平方和慣性周期的乘積。

表達形式：FKFH08參數化[45]是通過引入矢量流函數來實現：

式中，Ce為無量綱數，μ混合層垂直結構函數，h混合層厚度，g重力加速度，Δs水平網格距，ρ0為 Boussinesq密度常數，Lf亞中尺度渦寬度尺度，f科氏力參數，τ亞中尺度渦的時間尺度，z=δ-d，d為海水深度，δ為自由海表偏差，是混合層平均參考位密水平梯度。寫為分量形式：

這些公式適用于混合層，利用水平浮力梯度進行參數化：-ρ0?b=g?γ=g(?θγ?θ+?Sγ?S)，這與局地位密梯度有關。鋒的尺度可以是常數，或通過斜壓Rossby半徑計算得到：混合層平均的浮力頻率。

示蹤物濃度受流函數的影響：

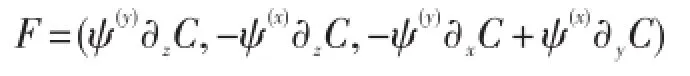
渦誘發速度表示為：

特征：在穩定層結情況下，FKFH08方案[45]的渦傳輸與GM90等[41]誘導速度傳輸不同。Fox-Kemper[47]等評估了FKFH08方案對全球海洋氣候模擬的影響。MOM[13]加入了該方案，對近海表混合層層化的弱偏差有改善。風-鋒、對流-鋒相互作用和鋒生過程等其它亞中尺度效應，目前尚未參數化。

2.12CB94波浪增強混合(Craig-Banner waveenhanced turbulence)

研究對象：在海洋表面，風將動量傳輸給海水。動量首先進入到表面波，通過波破碎傳遞給表面流場。相鄰海面的湍動能隨之增強，通過動量混合影響鄰近海表的洋流廓線。海表波動的潛在影響包括：產生斯托克斯漂移和雷諾應力[48]，影響平均流，以及波破碎時釋放混合下傳的湍動能。

理論依據：觀測表明，表面幾米的子層，湍流在海表波動作用下增強，該層的耗散率隨深度以3—4.6冪數遞減。CB94方案[29]將渦耗散表示為湍流速度和長度尺度的乘積，對波破碎的影響以海表能量源的形式進行參數化。在此波強化層，湍動能向下的通量由耗散平衡。

表達形式：湍動能方程為：

式中，k為湍動能，Kρ為湍流擴散系數，Km為湍流粘性系數，S2=(?zu)2+(?zv)2為切變產生項，l為長度尺度，MC為模式常數。Mellor和Blumberg[30]在以上方程右端加入浮力項作用-KHN2。

海表湍動能的邊界條件為：

Mellor等[30]對湍動能閉合模型進行了調整，以包含表面波破碎能量的效應，校正作用于表面長度尺度、湍動能取值和海-氣托曳系數。

特征：當混合層相對較淺時，使用CB94方案[29]對夏天海表溫度虛高的偏差有改進。NEMO[1]等模式采用了該參數化方案。

2.13 QYY04波致混合方案(Qiao-Yuan-Yang waveinduced vertical viscosity)

研究對象：近海溫度的垂直結構存在明顯的季節變化。模式模擬的夏季海表溫度通常偏高，上混合層偏淺，這可能是由上層混合強度不足導致的。波浪破碎在上層混合中發揮重要作用[29,49-50]，然而海洋模式對其模擬能力尚待提高。

理論依據：基于波流耦合模型[51]，假定波致混合項為波數譜的函數，得到波浪和潮流混合方案[52-53]。通過海浪的波數譜數值模式積分得到波浪方向譜，計算出隨時空變化的波致垂直粘性系數，將它作為垂直混合的一部分疊加到不同的湍流混合模型中，引入波浪運動對環流速度、溫度和鹽度的混合作用。

表達形式：將速度、溫度、鹽度等物理量分解為平均和脈動兩部分[52]：，其中脈動速度進一步分解為湍流部分和波致擾動：ui=uic+uiw。溫鹽擴散通量可表示為：

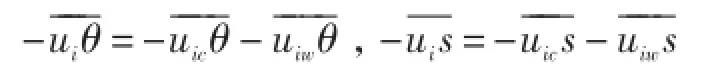
波致速度擾動可以用下式表示：

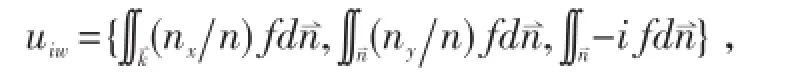
參數Kρ定義為波致垂直運動學粘性/擴散系數，依賴于混合長和波質點位移：

Kρ是決定波致混合的關鍵因子，應該考慮加入到海洋環流模式中。

特征：QYY04波致混合方案[52]對PP81和KPP94垂直混合方案均有顯著提升，可減小太平洋冷舌偏冷和過于西伸的偏差，對海洋上層溫度的模擬也有改善作用。

2.14 SJL04潮能耗散混合(Simmons-Jayne-LaurentMixingrelatedtotidalenergy dissipation)

研究對象：在層結海洋粗糙地形中，正壓潮和潮流會誘發內波之間的動量交換。其中，重力內波破碎能量來自潮與粗糙海底地形作用時正壓潮向內潮的能量散射；當潮流遇到大陸架時，發生底部拖曳摩擦。潮流模擬需要垂向幾米、水平1—10 km的分辨率，在全球氣候模式中難以實現，故有必要對其進行參數化處理。

理論依據：基于St Laurent等的理論[54]，Simmons等[55]將dianeutral參數化方案引入海洋環流模式，假定混合發生在一單位Prandtl數，強化等量的dianeutral示蹤擴散和動量粘性。當能量在小尺度耗散時，引起dianeutral混合。

表達形式：內潮破碎引起額外的垂直擴散項，表達為正壓潮向斜壓潮轉換的能量E的函數[54]：

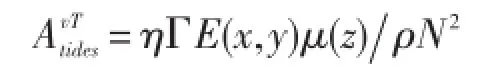
式中，η為潮耗散效率，典型取值為η=1/3，是局地耗散的部分內波能量通量，剩余部分作為低頻內波模態貢獻于背景內波場；Γ為混合效率，經常取值Γ=0.2。內波能量通量，ρ0為海水的參考密度，Nb是沿海床的浮力頻率，(n,Am)為地形粗糙度的波數和振幅，u為正壓潮速度，內波能量圖譜通過潮流正壓模型得出。描述湍流混合的垂直結構函數為：

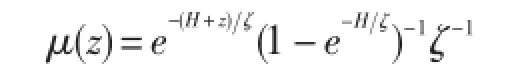
H為水柱總深度，ζ為湍流垂直耗散尺度。

海底拖曳引起的dianeutral擴散[13]可表示為：

式中，σ和χ分別為無量綱參數。

特征：SJL04方案[55]顯式給出了混合的潮能量，其混合系數隨時空變化。相比水平/垂直系數均一方案，SJL04方案會顯著降低溫度、鹽度模擬的偏差。MOM[13]和NEMO[1]都采用了該方案。

3 討論與結論

本文通過對海洋垂直混合過程參數化方案的回顧，總結了常用參數化類型的理論依據、數學表達及應用情況等。

在模式混合層的設定上，海洋垂直混合參數化方案可分為整體混合模型和連續混合層模型兩類[2]。整體模型假定海表邊界層完全湍流，在混合層厚度中速度、示蹤物分布均勻，如KT67方案[5]和PWP86方案[9]。結合KT67整體模型和PWP86模型中的梯度Richardson數判據，Chen等[56]提出了一種混合方案。由于整體方案無法分辨邊界層中的垂直結構，不能計算非局地混合，故其性能受到限制。

連續混合可以較好的反映混合層細節特征。在BL79方案[11]中，垂直混合系數不隨時間變化，僅為深度的簡單函數。另外一些方案將垂直湍流混合與大尺度海洋結構相聯系，例如，PP81方案[17]將這些系數規定為梯度Richardson數的函數。根據實驗觀測，GISS01模型[32-33]對Richardson數的取值進行了調整。值得注意的是，K理論在垂直混合方案中應用廣泛，它將垂直混合參數化為渦擴散和渦粘性系數(K)與平均量垂直梯度的乘積。MY82方案[22]引入多階預報方程求解不同湍流場，首先計算湍流混合長和速度尺度，然后確定垂直擴散和粘性系數。由于MY82方案[22]使用了相同的粘性和擴散長度尺度，GGL90方案[26]對其進行了改進，對粘性和擴散系數采用了不同的尺度。基于GLS03方案[34-35]的模擬結果表明，湍流長度尺度的選擇存在約束條件，該方案既可用做廣義長度尺度方案，還可以用來分析比較已有的模型。由于湍流混合模型計算較為復雜，KPP94方案[38-39]將大氣模式常用的K-profile parameterization(KPP)[57]方案引入海洋模式，旨在建立一個包含所有重要過程的參數化方案，它在相對粗糙的垂直網格上運行良好。

隨著觀測、理論和數值方法的發展以及硬件條件的提高，對于海洋的模擬越來越精細化，海洋中小尺度過程如中尺度渦旋、內波等過程的參數化受到人們的關注。GM90中尺度渦參數化提高了大多數z坐標模式的物理完整性。另外，FKFH08亞中尺度渦參數化對海洋上層的層結模擬有明顯改進。然而，目前中尺度渦、亞中尺度渦參數化仍然存在一些問題[3]，例如海洋內部中尺度渦閉合與邊界層方案的匹配問題、亞中尺度渦中的風-鋒相互作用、能量串級在模式中尚未考慮。更精確的衛星海面觀測對于中尺度渦的參數化過程有幫助。內波混合目前尚未有成熟的參數化方案，有待于進一步研究。

在海洋表面，波破碎對于動量由大氣風場向海洋流場的傳遞具有重要作用。CB94和QYY04分別發展了波浪混合參數化方案，對海洋上層溫度模擬的偏差有改善作用，并且加入QYY04方案還提高了PP81、KPP94參數化方案的性能。在海底地形作用下，正壓潮流的能量向斜壓潮流轉化，增強海洋底層物理要素的混合。SJL04方案將潮流耗散加入到混合過程參數化，改善了溫鹽的模擬，對大洋深海層結的模擬有重要作用。在海洋垂直混合過程中，一些模式也考慮了雙擴散[1,58]，溢流[13]等過程的影響。

當前海洋垂直混合參數化方案眾多，模式開發者一般選擇偏好的參數化方案并直接編碼進入模式。2014年在Breckenridge Colorado舉行的海洋模式工作組/通用地球系統模式(OMWG/CESM)會議上，Levy等人[59]提出了通用海洋垂直混合(CVMix)的構想，目標是建立一種包含一系列參數化方案的易用程式庫，最終實現參數化庫的獨立驅動。

隨著數值計算的發展，國內外涌現出了一些新的海洋模式[60]。如MITGCM[31]采用了非靜力框架，使其可以模擬多種尺度的流體現象，還使用了結構守恒映射，通過一種流體力學內核既可用于描述大氣又可用于海洋。在今后的工作中，我們將對這些模式進行詳細介紹。

致謝：論文的前期工作，受到與史珍博士共同調研工作的啟發，作者深表感謝。

[1]Madec G.NEMO ocean engine[M].Note du Pole de modélisation, Institut Pierre-Simon Laplace(IPSL),France,2008,27:1288-1619.

[2]Griffies S M,B?ning C,Bryan F O,et al.Developments in ocean climate modelling[J].Ocean Modelling,2000,2(3-4):123-192.

[3]Griffies S M,Adcroft A J,Banks H,et al.Problems and prospects inlarge-scaleoceancirculationmodels.In:ProceedingsofOceanObs'09:Sustained Ocean Observations and Information for Society[C].Venice,Italy,2010.

[4]范植松.海洋內部混合研究基礎[M].北京:海洋出版社,2002.

[5]Kraus E B,Turner J S.A one-dimensional model of the seasonal thermocline II.The general theory and its consequences[J].Tellus, 1967,19(1):98-106.

[6]Turner J S,Kraus E B.A one-dimensional model of the seasonal thermocline I.A laboratory experiment and its interpretation[J]. Tellus,1967,19(1):88-97.

[7]Wallcraft A,Metzger E,Carroll S.Software Design Description for the HYbrid Coordinate Ocean Model(HYCOM),Version 2.2[Z]. DTIC Document,2009.

[8]Bleck R.An oceanic general circulation model framed in hybrid isopycnic-Cartesian coordinates[J].Ocean Modelling,2002,4(1): 55-88.

[9]Price J F,Weller R A,Pinkel R.Diurnal cycling:Observations and models of the upper ocean response to diurnal heating,cooling,and windmixing[J].JournalofGeophysicalResearch:Oceans (1978-2012),1986,91(C7):8411-8427.

[10]Price J F,Mooers C N K,Van Leer J C.Observation and simulation of storm-induced mixed-layer deepening[J].Journal of Physical Oceanography,1978,8(4):582-599.

[11]Bryan K,Lewis L J.A water mass model of the world ocean[J]. Journal of Geophysical Research:Oceans(1978-2012),1979,84 (C5):2503-2517.

[12]Holland W.Energetics of barcoclinic oceans.In:Numerical Models of Ocean Circulation:Proceedings of a Symposium[C]. Washington,DC:NationalAcademy of Sciences,1975.

[13]Griffies S M.Elements of mom4p1[R].GFDL Ocean Group Techical Report 6,2010:444.

[14]Crawford W R,Osborn T R.Microstructure measurements in the AtlanticequatorialundercurrentduringGATE[J].Deep-Sea Research,1979,26:285-308.

[15]Osborn T R,Bilodeau L E.Temperature microstructure in the equatorial Atlantic[J].Journal of Physical Oceanography,1980,10 (1):66-82.

[16]Jones J H.Vertical mixing in the Equatorial Undercurrent[J]. Journal of Physical Oceanography,1973,3(3):286-296.

[17]Pacanowski R C,Philander S G H.Parameterization of vertical mixing in numerical models of tropical oceans[J].Journal of Physical Oceanography,1981,11(11):1443-1451.

[18]劉海龍,俞永強,李薇,等.LASG/IAP氣候系統海洋模式(LICOM1.0)參考手冊[M].北京:科學出版社,2004.

[19]Smith R,Gent P.Reference manual for the Parallel Ocean Program(POP),ocean component of the Community Climate System Model(CCSM2.0 and 3.0)[R].Technical Report LA-UR-02-2484,Los Alamos National Laboratory,Los Alamos, NM,2002.

[20]Mellor G L.Analytic prediction of the properties of stratified planetary surface layers[J].Journal of the Atmospheric Sciences, 1973,30(6):1061-1069.

[21]Mellor G L,Yamada T.A hierarchy of turbulence closure models for planetary boundary layers[J].Journal of the Atmospheric Sciences,1974,31(7):1791-1806.

[22]Mellor G L,Yamada T.Development of a turbulence closure model for geophysical fluid problems[J].Reviews of Geophysics, 1982,20(4):851-875.

[23]Martin P J.Simulation of the mixed layer at OWS November and Papa with several models[J].Journal of Geophysical Research: Oceans(1978-2012),1985,90(C1):903-916.

[24]Kantha L H,Clayson C A.An improved mixed layer model for geophysical applications[J].Journal of Geophysical Research: Oceans(1978-2012),1994,99(C12):25235-25266.

[25]Mellor G L.User's guide for a three-dimensional,primitive equation,numerical ocean model[M].Princeton,NJ:Atmospheric and Oceanic Sciences Program,Princeton University,1998.

[26]Gaspar P,Grégoris Y,Lefevre J M.A simple eddy kinetic energy model for simulations of the oceanic vertical mixing:Tests at station Papa and Long-Term Upper Ocean Study site[J].Journal of Geophysical Research:Oceans(1978-2012),1990,95(C9): 16179-16193.

[27]Bougeault P,Lacarrere P.Parameterization of Orography-Induced Turbulence in a Mesobeta--Scale Model[J].Monthly Weather Review,1989,117(8):1872-1890.

[28]Madec G,Delecluse P,Imbard M,et al.OPA 8.1,ocean general circulationmodelreferencemanual[M].NoteduP?lede modélisation,Institut Pierre-Simon Laplace,1998,11:97.

[29]Craig P D,Banner M L.Modeling wave-enhanced turbulence in the ocean surface layer[J].Journal of Physical Oceanography, 1994,24(12):2546-2559.

[30]Mellor G,Blumberg A.Wave breaking and ocean surface layer thermal response[J].Journal of Physical Oceanography,2004,34 (3):693-698.

[31]Adcroft A,Campin J M,Dutkiewicz S,et al.MITgcm user manual [M].MIT Department of EAPS,Cambridge,2008.

[32]Canuto V M,Howard A,Cheng Y,et al.Ocean Turbulence.Part I: One-PointClosureModel-MomentumandHeatVertical Diffusivities[J].Journal of Physical Oceanography,2001,31(6): 1413-1426.

[33]Canuto V M,Howard A,Cheng Y,et al.Ocean turbulence.Part II: Vertical diffusivities of momentum,heat,salt,mass,and passive scalars[J].JournalofPhysicalOceanography,2002,32(1): 240-264.

[34]Umlauf L,Burchard H.A generic length-scale equation for geophysical turbulence models[J].Journal of Marine Research, 2003,61(2):235-265.

[35]Umlauf L,Burchard H.Second-order turbulence closure models for geophysical boundary layers.A review of recent work[J].Continental Shelf Research,2005,25(7-8):795-827.

[36]Rodi W.Examples of calculation methods for flow and mixing in stratified fluids[J].Journal of Geophysical Research:Oceans (1978–2012),1987,92(C5):5305-5328.

[37]Wilcox D C.Reassessment of the scale-determining equation for advanced turbulence models[J].AIAA Journal,1988,26(11): 1299-1310.

[38]Large W G,McWilliams J C,Doney S C.Oceanic vertical mixing:A review and a model with a nonlocal boundary layer parameterization[J].ReviewsofGeophysics,1994,32(4): 363-403.

[39]Large W G,Danabasoglu G,Doney S C,et al.Sensitivity to surface forcing and boundary layer mixing in a global ocean model:Annual-meanclimatology[J].JournalofPhysical Oceanography,1997,27(11):2418-2447.

[40]Gent P R,Mcwilliams J C.Isopycnal mixing in ocean circulation models[J].Journal of Physical Oceanography,1990,20(1): 150-155.

[41]Gent P R,Willebrand J,McDougall T J,et al.Parameterizing eddy-induced tracer transports in ocean circulation models[J]. Journal of Physical Oceanography,1995,25(4):463-474.

[42]Redi M H.Oceanic isopycnal mixing by coordinate rotation[J]. Journal of Physical Oceanography,1982,12(10):1154-1158.

[43]Griffies S M.The gent-mcWilliams skew flux[J].Journal of Physical Oceanography,1998,28(5):831-841.

[44]Boccaletti G,Ferrari R,Fox-Kemper B.Mixed layer instabilities and restratification[J].Journal of Physical Oceanography,2007,37 (9):2228-2250.

[45]Fox-Kemper B,Ferrari R,Hallberg R.Parameterization of mixed layer eddies.Part I:Theory and diagnosis[J].Journal of Physical Oceanography,2008,38(6):1145-1165.

[46]Fox-Kemper B,Ferrari R.Parameterization of mixed layer eddies. Part II:Prognosis and impact[J].Journal of Physical Oceanography,2008,38(6):1166-1179.

[47]Fox-Kemper B,Danabasoglu G,Ferrari R,et al.Parameterization of mixed layer eddies.III:Implementation and impact in global ocean climate simulations[J].Ocean Modelling,2011,39(1-2): 61-78.

[48]Phillips O M.The dynamics of the upper ocean[M].Cambridge: Cambridge University Press,1977.

[49]Mellor G L.One-dimensional,ocean surface layer modeling:A problem and a solution[J].Journal of Physical Oceanography, 2001,31(3):790-809.

[50]Mellor G.The three-dimensional current and surface wave equations[J].Journal of Physical Oceanography,2003,33(9): 1978-1989.

[51]Yuan Y,Qiao F,Hua F,et al.The development of a coastal circulationnumericalmodel:1.Wave-inducedmixingand wave-current interaction[J].Journal of Hydrodynamics,Ser.A, 1999,14:1-8.

[52]Qiao F L,Yuan Y,Yang Y Z,et al.Wave-induced mixing in the upper ocean:Distribution and application to a global ocean circulation model[J].Geophysical Research Letters,2004,31(11).

[53]喬方利,馬建,夏長水,等.波浪和潮流混合對黃海、東海夏季溫度垂直結構的影響研究[J].自然科學進展,2004,14(12):1434-1441.

[54]St Laurent L C,Simmons H L,Jayne S R.Estimating tidally driven mixing in the deep ocean[J].Geophysical Research Letters,2002,29(23):21-1-21-4.

[55]Simmons H L,Jayne S R,St Laurent L C,et al.Tidally driven mixing in a numerical model of the ocean general circulation[J]. Ocean Modelling,2004,6(3-4):245-263.

[56]Chen D,Rothstein L M,Busalacchi A J.A hybrid vertical mixing scheme and its application to tropical ocean models[J].Journal of Physical Oceanography,1994,24(10):2156-2179.

[57]Holtslag A A M,Boville B A.Local versus nonlocal boundarylayer diffusion in a global climate model[J].Journal of Climate, 1993,6(10):1825-1842.

[58]Merryfield W J,Holloway G,Gargett A E.A global ocean model with double-diffusive mixing[J].Journal of Physical Oceanography,1999,29(6):1124-1142.

[59]Levy M,Danabasoglu G,Griffies S,et al.Community Ocean Vertical Mixing(CVMix)Status Update[Z].OMWG Meeting. Breckenridge,CO,2014.

[60]鄭沛楠,宋軍,張芳苒,等.常用海洋數值模式簡介[J].海洋預報,2008,25(4):108-120.

Review of vertical mixing parameterization in ocean climate modeling

WANG Lei1,2,WANG Zhang-gui2,LING Tie-jun2,ZUO Jin-qing3
(1.School of Physics,Peking University,Beijing 100871 China;2.Key Laboratory of Research on Marine Hazards Forecasting,NMEFC,Beijing 100081 China;3.Laboratory for Climate Studies,National Climate Center,China Meteorological Administration,Beijing 100081 China)

In ocean climate models,the parameterization schemes of vertical mixing processes are introduced. Firstly,the corresponding physical issues,theoretical basis,numerical expressions and characteristics of various vertical mixing parameterization schemes are introduced,and the evolutions of different schemes are shown. Secondly,the latest advancement about vertical mixing parameterization,owing to considering the contribution from the mesoscale eddies,submesoscale eddies,wave and tidal are summarized.Finally,we propose some suggestions on the future development in vertical mixing models.

turbulence closure scheme;mesoscale eddies mixing;submesoscale eddies mixing;wave induced mixing;tidal induced mixing

P731

：A

：1003-0239（2014）05-0093-12

10.11737/j.issn.1003-0239.2014.05.015

2014-06-02

國家重點基礎研究發展計劃(2010CB950303)；國家自然科學基金(41376016，41205058)；國家重點基礎研究發展計劃(2014CB745004)

汪雷（1984-），男，助理研究員，主要從事擾動位能、季風、海洋模式研究。E-mail:wangl@nmefc.gov.cn