一種改進的低復雜度變步長LMS算法*

強建龍,蔡燦輝

(華僑大學信息科學與工程學院,福建廈門361021)

一種改進的低復雜度變步長LMS算法*

強建龍,蔡燦輝

(華僑大學信息科學與工程學院,福建廈門361021)

改進型的變步長LMS算法在有效抑制瞬時噪聲對經典的變步長LMS算法影響的同時,也增加了算法的計算復雜度,提高了其硬件實現的難度。為降低變步長LMS算法的計算復雜度,提出了一種步長改變因子與前后兩個時刻誤差的乘積成正比的新的變步長LMS改進算法,在不增加計算復雜度的條件下,有效地抑制了瞬時噪聲對迭代步長的影響。仿真結果表明,提出的算法和現有的變步長LMS算法收斂速度相當,但其穩態誤差更小,計算復雜度也更低,有利于算法的硬件實現。

最小均方算法 變步長 均方誤差 計算復雜度 仿真

0 引 言

最小均方誤差(LMS)濾波算法具有簡單有效、計算量小、易于實現等優點,因此在工程中得到了廣泛的應用。LMS算法中的步長因子μ決定抽頭系數向量在每次迭代中的更新幅度,是影響算法收斂速度的關鍵參數。LMS算法的目的是在更新過程中使得抽頭權向量逼近維納濾波器的抽頭權向量,因此,更新過程也稱之為學習過程。μ決定了LMS算法的收斂速度,同時直接影響到穩態均方誤差。大的學習速率能夠提高算法的收斂速度,但會加大穩態誤差；反之,如果為了提高穩態性能而采用小的學習速率時,收斂速度就會變慢。兼顧LMS算法的穩態性能和收斂速度最簡單而有效的方法就是在不同的迭代時期使用不同的學習速率,也就是采用變步長學習速率。

為此,Kwong和Johnston[1]在1992年提出了標志性的變步長(VSS,Variable Step Size)LMS算法,該算法根據預測誤差的平方調節學習速率。在此基礎上,Aboulnasr等[2]于1997年提出一種改進的變步長(MVSS,Modified Variable Step Size)LMS算法,利用相鄰時刻誤差的互相關函數很好地避免了不相關的噪聲對迭代步長的影響,但是計算復雜度比VSS-LMS也有所增加。Pazaitis等[3]提出的變步長LMS算法利用誤差的峰度控制步長因子,該算法利用了近似高斯信號的特性,對于較低高斯噪聲有很好的效果,但該近似在較高的噪聲條件下并不準確。Mader等[4]提出了最優變步長LMS算法,該算法的設計是基于每一步迭代中,使得均方權值偏差(MSD,Mean Square Deviation)的下降達到最大,其中MSD被定義為E{(ω(n)-ω0(n))2},即當前濾波器的抽頭系數ω(n)與維納-霍夫方程定義的抽頭權向量的最優值ω0(n)之差,然而ω0(n)在迭代過程中是不可知的[5],所以該算法實用性差。Hwang等[6]提出的VSLMS,利用輸入信號與誤差乘積的范數更新步長因子,但計算復雜度太高,難以實現。為了進一步提高變步長LMS的性能,文中在VSS-LMS和MVSS-LMS算法的基礎上,提出了一種新的改進型變步長LMS算法,根據當前時刻與前一時刻誤差能量的幾何平均自適應調整學習速率,有效地降低了計算復雜度。

1 變步長LMS濾波算法

1.1 LMS自適應濾波算法

LMS自適應濾波就是根據估計誤差的大小自動調節FIR濾波器的抽頭系數,使其代價函數最小的一種算法。設x(n)是濾波器的輸入向量,y(n)是濾波器的輸出向量,ω(n)是濾波器的抽頭系數,則有

設d(n)是期望信號,則是濾波器的輸出信號y(n)與期望信號d(n)的差e(n)可表示為:

最常用的濾波器設計準則是最小均方誤差(MMSE)準則,也就是使濾波器實際輸出與期望響應之間的均方誤差最小,其代價函數定義為:

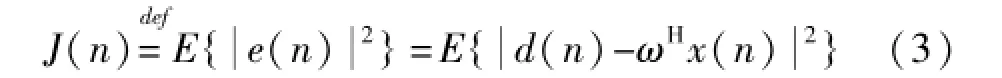
濾波器的設計就是要找到使J(n)最小的濾波器系數矩陣ω(n)。采用梯度下降法求解,有

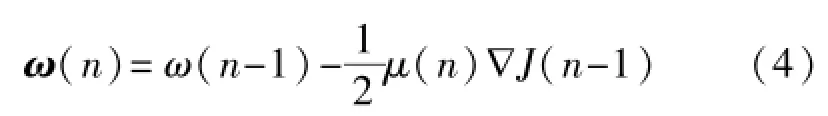
式中[7]:

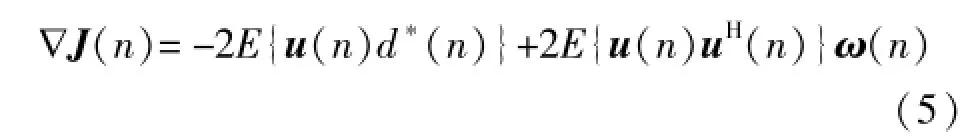
容易驗證,瞬時梯度向量是真實梯度向量的無偏估計:

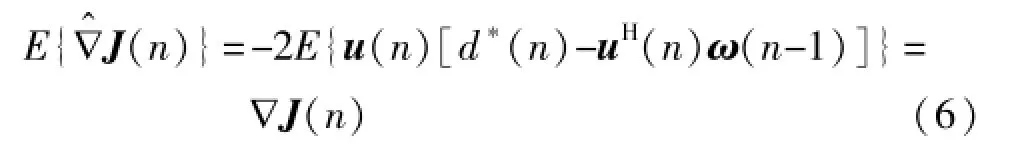
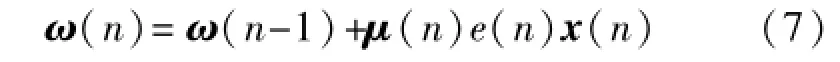
式(7)所示的算法就是Widrow[8]于1960年提出的LMS濾波算法。若μ(n)是常數,則稱之為固定步長LMS濾波算法,否則稱之為變步長LMS濾波算法。

1.2 變步長LMS濾波算法

從式(7)可知,加大步長可以提高收斂速度,但同時也會加大穩態誤差；反之,降低步長能減小穩態誤差,但卻會降低收斂速度。為了提高LMS算法的性能,Kwong和Johnston于1992年提出了一種具有代表性的變步長LMS(VSS-LMS)濾波算法,即在誤差較大時采用大的迭代步長以提高收斂速度,在誤差較小時采用小的迭代步長以減小穩態誤差。VSS -LMS濾波算法的步長迭代計算表達式如下:

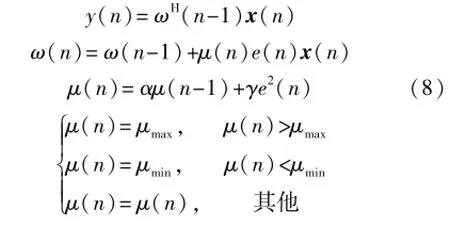
式中,0＜α＜1,γ＞0,μmax≤,μmin=10-5[1], tr(R)是相關矩陣R的跡,根據矩陣代數,我們還知道,一個正方矩陣的跡等于它的對角元素之和。當橫向濾波器是空域濾波器時,其M個輸入端的輸入信號分別是M個傳感器的觀測數據。此時,空域濾波器的輸入信號向量為u(n)=[u1(n),u2(n),…,uM(n)]是輸入信號ui(n)的均方值或能量。因此相關矩陣R的跡等于在濾波器M個輸入端上測得的總的輸入能量,也就是[6]

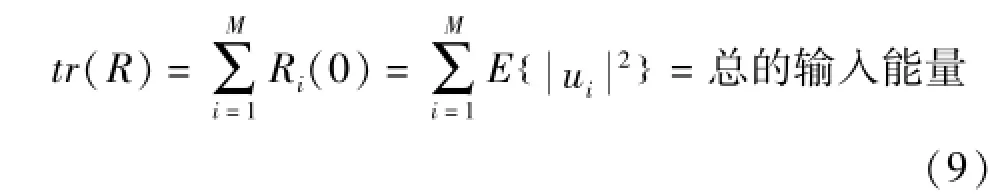
由此可知,tr(R)也就是輸入信號的能量,這表明使得該算法收斂的條件也可以寫成:

從式(8)可知,噪聲的瞬時變化對VSS-LMS濾波算法的迭代步長會產生較大的影響。為此, Aboulnasr在1997年提出了一種改進的變步長LMS濾波算法(MVSS-LMS),在該算法中,步長由平滑后的相鄰時刻誤差的互相關函數控制,算法描述如下:

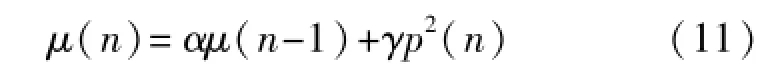
其中:

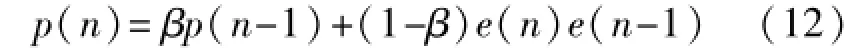
這里,α,β,γ均為常數,且β趨近于1,p(n)是誤差自相關估計因子。從式(11)、式(12)可知,與Kwong提出的算法相比,Aboulnasr的算法用誤差信號的自相關估計因子p(n)替代誤差函數e(n)。由于誤差自相關函數的變化能滿足期望的迭代步長變化的要求,同時,誤差信號的自相關運算使得Aboulnasr的算法能較好地避免了在步長迭代過程中不相關噪聲的影響,因此Aboulnasr的算法在不相關噪聲背景下具有更好的收斂性能。然而,誤差自相關估計因子的計算增加了算法的計算復雜度。

為了強化信號對學習因子的影響,Hwang[6]從另一個角度對VSS-LMS濾波算法進行改進,步長由平滑后的的誤差與輸入的互相關函數和誤差能量的乘積控制,算法描述如下:

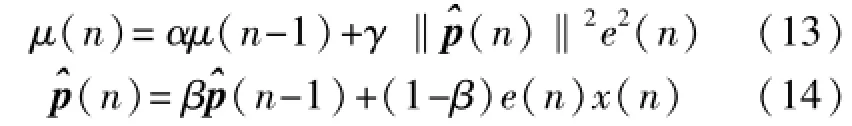
這里,‖·‖2代表平方歐式范數操作。該方法通過控制(n),使得步長的變化隨輸入信號的變化而變化,較好地抑制了不相關噪聲對弱信號的影響。然而該方法需要計算范數,大大增加了算法的計算復雜度。

1.3 所提出的變步長LMS濾波算法

為了減少算法的計算復雜度,文中對式(8)進行修改,提出一種簡化的相關學習算法,步長因子迭代過程如下所示:

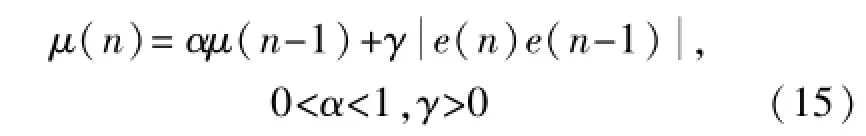
比較式(8)與式(13)不難看出,所提出的算法是用前一時刻的誤差能量和當前時刻的誤差能量的幾何平均代替VSS-LMS算法中的當前時刻誤差能量,這樣可以在有效抑制不相關噪聲的同時,大大降低了計算復雜度。

1.4 計算復雜度分析

表1給出了是文中所提出的簡化相關變步長LMS算法迭代步驟,以及所需的乘加次數。其中,N是濾波器的階數。

表1 所提出算法迭代步驟Table 1 Iteration steps of the proposed algorithm

表2列出了文中所提出的算法和VSS-LMS、MVSS-LMS以及VSLMS-LMS三個典型的變步長算法的計算復雜度比較數據。

表2 典型變步長算法的計算復雜度比較Table 2 Comparison on computational complexity of typical variable step size algorithms

實際應用中通常采用的是8階濾波器[9],對應的VSS-LMS、MVSS-LMS、VSLMS-LMS和文中算法所需的乘法次數分別為20、23、46和20,即文中算法所需的乘法次數和經典的VSS-LMS算法一樣,比MVSS-LMS減少了15%,比VSLMS-LMS減少了130%。上述算法所需的加法次數分別為17、18、32、17,而文中算法和VSS-LMS一樣,比MVSS-LMS少約6%,比VSLMS-LMS少88%。

2 仿真分析

為了對文中所提出算法的收斂性能進行更為準確的測試,采用Monte Carlo方法進行仿真,文中采用的是2 000次獨立運行結果的統計平均。圖1和圖2是信噪比分別為0 dB和10 dB時文中算法與幾種典型的變步長LMS算法的均方誤差曲線的仿真對比圖。其中,各算法的參數設置如表3所示。輸入x(n)為正弦信號與白噪聲的合成,

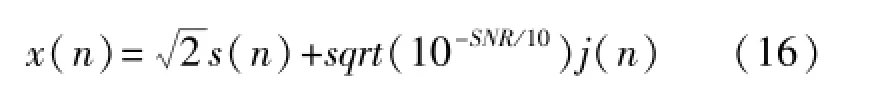
式中,s(n)為正弦信號序列,j(n)為均值為0、功率為1的高斯白噪聲,SNR為信噪比(單位為dB)。通過圖1和圖2可以看出文中提出的算法具有最小的穩態均方誤差。

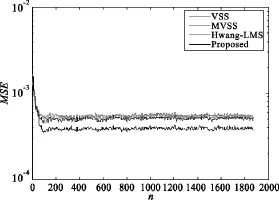
圖1 信噪比為0 dB時均方誤差曲線Fig.1 Comparison on MSE of various adaptive algorithms(SNR=0 dB)

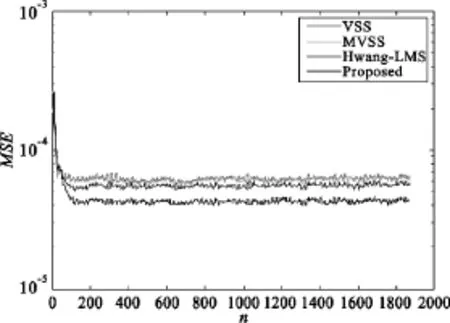
圖2 信噪比為10 dB時均方誤差曲線Fig.2 Comparison on MSE of various adaptivealgorithms(SNR=10 dB)

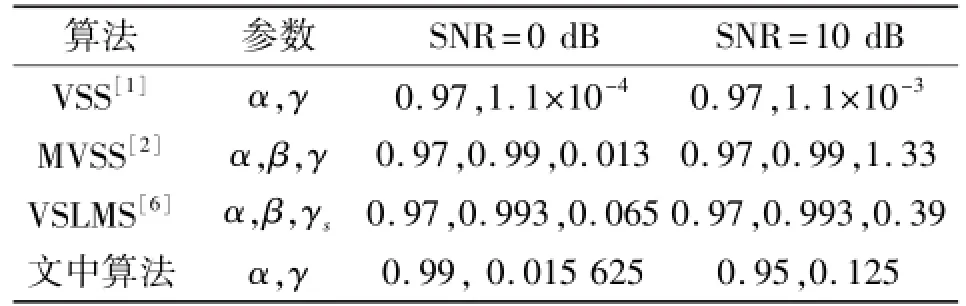
表3 參數設置Table 3 Parameter settings

3 結 語

文中在分析了現有的變步長LMS算法基礎上,提出了一種步長改變因子與前后兩個時刻誤差的乘積成正比的新的變步長LMS改進算法,能夠在不增加計算復雜度的條件下,有效地抑制瞬時噪聲對迭代步長的影響。仿真結果表明,和現有算法相比較,文中提出的算法具有穩態誤差小、計算復雜度低等優點,有利于在乘法器資源有限的FPGA或者DSP上實現。

[1] KWONG R H,JOHNSTON E W.A Variable Step Size LMS Algorithm[J].Signal Processing,IEEE Transactions on,1992,40(07):1633-1642.

[2] ABOULNASR T,MAYYAS K.A Robust Variable Stepsize LMS-type Algorithm:Analysis and Simulations[J]. Signal Processing,IEEE Transactions on,1997,45(03): 631-639.

[3] PAZAITIS D I,CONSTANTINIDES A G.A Novel Kurtosis Driven Variable Step-size Adaptive Algorithm[J]. Signal Processing,IEEE Transactions on,1999,47(03): 864-872.

[4] MADER A,PUDER H,SCHMIDT G U.Step-size Control for Acoustic Echo Cancellation Filters-an Overview [J].Signal Processing,2000,80(09):1697-1719.

[5] 李寧.LMS自適應濾波算法的收斂性能研究與應用[D].哈爾濱:哈爾濱工程大學,2009.

LI Ning.Convergence Performance Analysis and Applications of the Adaptive lease Mean Square(LMS)Algorithm [D].Harbin:Harbin Engineering University,2009.

[6] HWANG J K,LI Y P.Variable Step-Size LMS Algorithm with a Gradient-based Weighted Average[J].Signal Processing Letters,IEEE,2009,16(12):1043-1046.

[7] 張賢達.現代信號處理[M].第2版.北京:清華大學出版社有限公司,2002:188-199.

ZHANG Xian-da.Modern Signal Processing[M].Second Edition.Beijing:Tsinghua University Publishing Company,2002:188-199.

[8] WIDROW B.Adaptive Signal Processing[M].STEARNS S D.Englewood Cliffs,NJ:Prentice-Hall,1985:75-87.

[9] 劉忠樂,蔡燦輝,強建龍.基于RLS_DGD的查找表更新算法[J].通信技術,2013,46(05):111-114.

LIU Zhong-le,CAI Can-hui,QIANG Jian-long.Lookup Table Update Algorithm based on RLS_DCD[J]. Communications Technology,2013,46(05):111-114.

QIANG Jian-long(1987-),male,graduate student,majoring in mobile communication.

蔡燦輝(1954—),男,博士,教授,主要研究方向為圖像處理與信息編碼。

CAI Can-hui(1954-),male,Ph.D.,professor,mainly engaged in image processing and information coding.

An Improved Low Computational Complexity Variable Step Size LMS Algorithm

QIANG Jian-long,CAI Can-hui
(College of Information Science and Technology,Huaqiao University,Xiamen Fujian 361021,China)

Although the modified variable step size LMS algorithm can effectively suppress the instant noise interferences on the step size,its computational complexity is increased.Consequently,the difficulty for the hardware realization is increased.In order to reduce the complexity of the variable step size LMS algorithm,a novel modified variable step size algorithm with step variation proportional to the product of current error and previous error is proposed in this paper.The proposed algorithm can well restrain the instant noise interferences without increasing the computational complexity.The simulation results indicate that compared with the existing variable step size of LMS algorithms,the convergence speed of the proposed algorithm is about the same,but its steady-state error is much smaller.Meanwhile,its computational complexity is lower,and favorable to hardware realization.

LMS(Least Mean Square)algorithm；variable step size；mean squared error；computational complexity；simulation

TN929.5

A

1002-0802(2014)03-0258-04

10.3969/j.issn.1002-0802.2014.03.005

強建龍(1987—),男,碩士研究生,主要研究方向為移動通信；

國家自然科學基金(No.61201264)項目名稱:高敏捷性的融合協同及部分中繼協同主用戶檢測研究

Foundation Item:The key technology of mobile broadband wireless access system research and industrialization(No.61201264)