基于局部聚合的復雜網絡自動聚簇算法
湯 蓉,唐常杰,徐開闊,楊 寧
(1. 成都信息工程學院計算機學院 成都 610225; 2. 四川大學計算機學院 成都 610065)
現實世界中的諸多系統均可建模為復雜網絡(complex network),如:WWW萬維網、人際關系網、流行病傳播網等。系統中的實體(entity)由節點(node)表示,而實體之間的關聯(interaction/relation)由邊(edge)表示,節點集和邊集構成了復雜網絡。復雜網絡的社區結構(network community/cluster structure)是描述復雜網絡拓撲結構的重要特性之一,具有社區內部節點連接緊密而社區之間連接相對疏松的特點[1]。隨著計算機技術的發展,可得到的數據規模越來越大,從規模巨大的網絡數據中發現社區結構從而挖掘網絡中隱藏的規律已變得越來越重要。
迄今為止,研究者們提出了諸多不同的發現社區結構的方法[1-6],如:文獻[5]提出的快速啟發式算法,文獻[6]提出的基于子圖相似度的貪婪聚簇算法等,其中大部分為全局聚簇(global clustering)算法。很多文獻中使用的快速隨機遞歸搜索算法(fast stochastic and recursive search algorithm)[3-4,7-8],根據特定的全局模塊性,如:Q函數(modularity)[2]和網絡最短描述長度(network minimum description length,NMDL)等[3-4],利用全局信息(global information),對所有的點和邊同時展開搜索從而揭示網絡社區結構,導致聚簇時間和空間消耗偏高。因全局聚簇需預先掌握網絡的全局連接信息,有些還需預知簇數,使其對于動態網絡和大型網絡具有局限性。
文獻[7]首先提出了局部簇(local cluster)和局部模塊性(local modularity)的概念,并基于最大化局部模塊性提出了局部聚簇(local clustering)算法[7]。隨后研究者們又提出了其他局部模塊性定義,包括:Outwardness(OW)[9]、 ModularityM(MM)[10]和LMetric(LMe)[11]等。因局部聚簇無需全局信息,通過計算單個簇的模塊性搜索局部簇,特別適應于動態網絡和大型網絡的已知區域。
針對全局聚簇算法空間和時間消耗偏高的缺陷,本文基于局部聚簇提出了一種兩段式(two-phase)的復雜網絡自動聚簇算法(local agglomeration and iterative clustering algorithm, LAICA)。該算法分為兩個階段:局部聚合(local agglomeration)階段和局部簇迭代聚簇(iteratively clustering of local clusters)階段。第一階段通過局部聚簇發現網絡中局部密集的節點集,獲得由局部簇構成的復雜網絡局部簇結構;第二階段通過迭代式全局聚簇網絡的局部簇結構自動解析網絡的最優社區結構。本文選擇了4種局部模塊性作為局部簇搜索的評價標準;因Q函數存在分辨極限[12],全局模塊性則采用基于信息論的網絡最短描述長度—Map Equation(ME, 映射方程式)[4]。使用多個真實網絡對LAICA算法進行了聚簇實驗,兩個階段中不同的局部模塊性和全局模塊性的結合使用,使LAICA算法表現的聚簇性能不同。和其他全局聚簇算法比較,LAICA算法的聚簇無需所有節點參與,僅從一組初始節點開始發現局部簇;對局部簇的迭代聚合,使算法能夠自動解析網絡的社區數量,并同時精確地將節點分配至其所屬社區。實驗的聚簇精度(NM I值)最高達99.72%,表明LAICA是一個精確的復雜網絡自動聚簇算法。
1 復雜網絡聚簇基本概念
復雜網絡可建模為圖:X = (V,E), 其中:X為復雜網絡,V為節點集,E為邊集。復雜網絡中局部連接緊密的節點集形成了網絡的社區(community/cluster)。設X包含n個節點且分布于m個社區中,形成了X特定的社區結構:M = {M1, M2,…,Mi,…, Mm},其中:Mi(1≤i≤m)為X的任一社區且Mi∈V。
1.1 局部簇結構模型
從單個節點出發,利用該節點的連接信息所發現的局部密集的節點集,稱為復雜網絡的局部簇[7]。局部簇Mi的節點集如圖1所示。局部簇中所有節點構成其成員節點集(member nodes),以Mi表示。成員節點又可分為兩個子集:邊界成員節點集(boundary nodes, Bi)和核心成員節點集(core nodes, Ci),即:Mi= CiUBi,其中:邊界成員節點至少存在一條邊與簇外節點相連,而核心成員節點僅與簇內成員節點相連。Mi的簇外節點,如果至少存在一條邊與Mi的成員節點相連,則為Mi的鄰居節點,Mi的鄰居節點集(shell nodes)以Si表示。連接不同節點集之間的邊形成了不同的邊集,包括:內邊集(inlinks)、外邊集(outlinks)/邊界外邊集(outlinks/Boutlinks)和邊界內邊集(boundary inlinks, Binlink),其中:內邊為連接Mi成員節點之間的邊;外邊(也稱為邊界外邊)為Mi的邊界成員節點與鄰居節點之間的邊。邊界內邊集和邊界外邊集的并集稱之為邊界邊集,即:與邊界成員節點相連的所有邊的集合[11]。
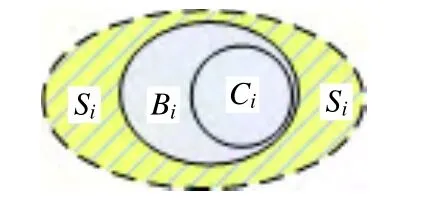
圖1 局部簇Mi的節點集
1.2 局部模塊性
局部聚簇的基本思路如下:選擇初始節點vi,以vi建立初始局部簇Mi;搜索最大化Mi局部模塊性變化值的鄰居節點聚合到Mi中,更新Mi的成員節點集和鄰居節點集;直到Mi不再存在能改善其局部模塊性的鄰居節點,則停止對局部簇Mi的搜索和擴展[7]。如表1所示,以下4種不同的局部模塊性:Local Modularity(LM)[7]、 ModularityM(MM)[10]、 Lmetric(LMe)[11]和Outwardness(OW)[9],均利用社區結構中社區內連接緊密而社區間連接疏松的特點,以簇內連接與簇外連接之間的比值或差值來表示局部簇的局部模塊性;但卻采用局部簇的不同屬性值來量化簇內連接與簇外連接。其中:LM、MM和LMe均采用簇內連接與簇外連接之間的比值表示局部模塊性,但OW定義的不是局部簇Mi的模塊性,而是Mi的單個鄰居節點連接簇內與簇外節點的邊數之差。

表1 局部模塊性評價標準的定義和計算公式
2 基于局部聚合與迭代的自動聚簇
LAICA算法分為兩個階段:局部聚合階段和局部簇迭代聚合階段。LAICA算法引入針對網絡聚簇問題的概念:子簇網絡結構。


2.1 局部聚合算法
以每一個初始節點vi為首個成員建立初始局部簇Mi,然后逐步聚合最大化Mi局部模塊性的鄰居節點,直到Mi不再存在鄰居節點能改善其局部模塊性,則停止對Mi的搜索。當Mi不存在鄰居節點能改善其局部模塊性時,稱Mi不可再擴展(un-expandable)。對于復雜網絡X,如果其所有局部簇都不可再擴展或其所有節點均已聚合到局部簇中,則稱X不可再擴展,此時停止搜索并輸出所得到的X的局部簇網絡結構,如算法1所示。


2.2 局部簇迭代合并算法
通過局部聚簇X¢到一組局部簇。所有局部簇和未被聚合到局部簇的其他節點則構成了X¢的局部簇網絡結構X¢,其中每一個局部簇或節點均為X¢的聚簇單元(clustering unit)。局部簇迭代合并算法(iteratively clustering of local clusters, ICLC)通過最大化X¢的全局模塊性,迭代合并(iteratively merge)X¢的聚簇單元從而搜索X的最優社區結構。
2.1.1 全局模塊性
Q函數[2]已被文獻廣泛使用。而Map Equation是根據香農的源編碼理論(source coding theorem)[14]提出的另一種全局模塊性[4]。設復雜網絡X包含n個節點和l條邊,且其節點分布在m個簇中,M表示包含該m個簇的特定社區結構,Q函數和ME的定義和計算公式分別如下:
1) Network Modularity(Q函數)
Q函數為社區內實際連接數目與隨機連接情況下社區內期望連接數目之差,如式(1)所示,式中:i表示第i個社區,lii為第i個社區的邊數,di為第i個社區節點的總度數(degree)。對于特定社區結構M,Q值越大,則M的網絡模塊度越強:
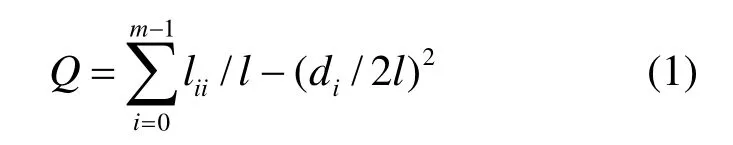
2) Map Equation(ME, 映射方程式)
以L(M)表示社區結構M的ME值。對于無向網絡,L(M)的定義如式(2)所示,式(2)中參數含義及計算公式參考文獻[4]。對于特定社區結構M,L(M)的值越小,則M的網絡模塊度越強,能更精確描述網絡的社團結構[4]。
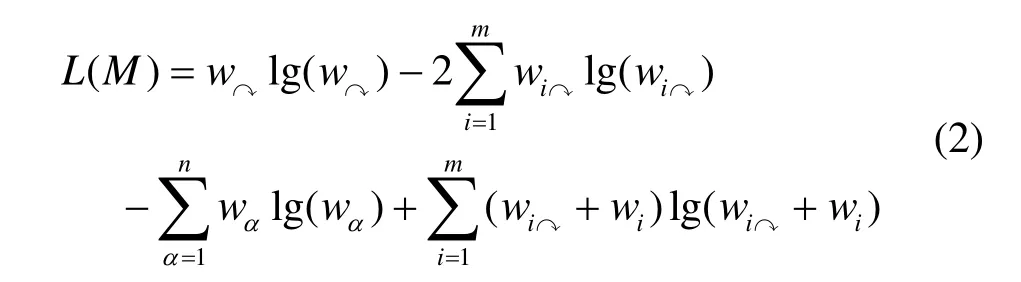
2.1.2 局部簇迭代合并
定義每一個聚簇單元中節點的數量為聚簇單元的長度(length)。迭代聚簇的每一步,均選擇X¢中長度最短的聚簇單元Umin,通過計算Umin與每一個鄰居單元合并后X¢的全局模塊性變化值:DME。選擇最大化DME的鄰居單元與Umin聚合。直到X¢的小于某一個閾值e,即:DME,則終止迭代合并,并輸出所獲得的社區結構,如算法2所示。

2.3 算法復雜度分析
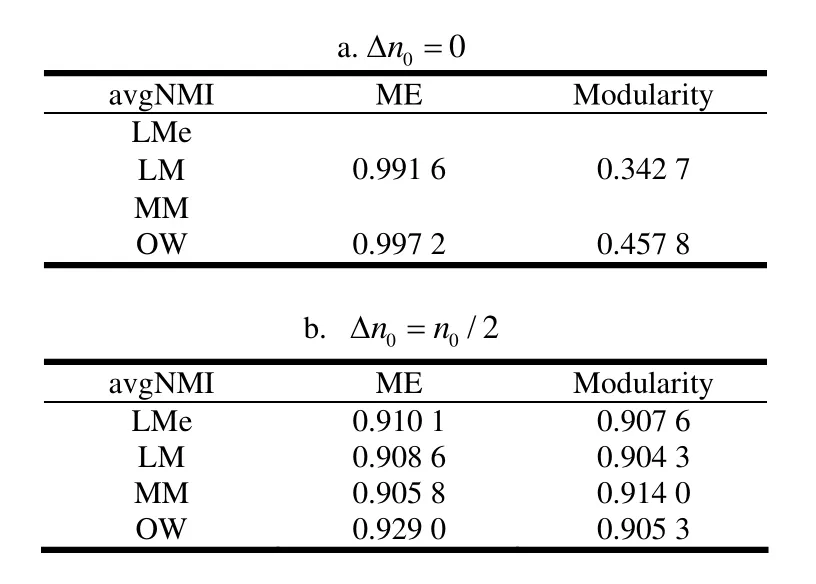
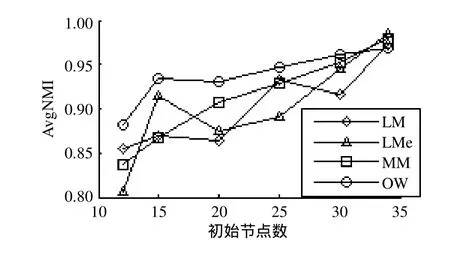
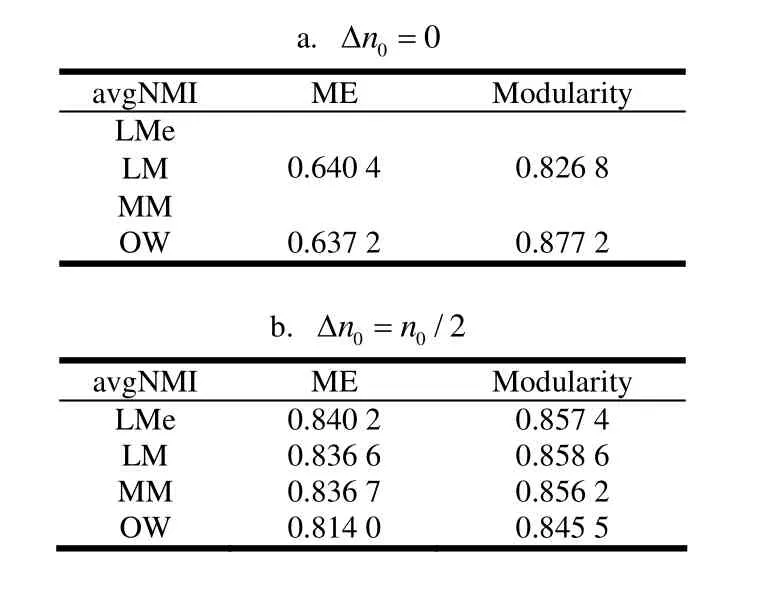
首先分別對算法兩個階段的復雜度進行分析。設m¢為局部簇個數(m¢ 1) 局部聚合算法(LAA)的復雜度 對于LAA算法,ModularityM、LMetric和LocalModularity的復雜度均為O(k2d)[7,11,13]。對于真實網絡,添加新節點的時間消耗決定了局部簇搜索的復雜度為O(k)[7,11,13]。 因outwardness僅需在局部簇的鄰居節點中搜索outwardness值最大的節點v,且當v聚合到局部簇時,僅v的簇外鄰居節點發生變化,所以聚合時僅需更新v的簇外鄰居節點的outwardness值。因為在v和每一個鄰居節點之間有且僅有一條邊,所以對于每一個簇外鄰居節點:Δoutwardness = -2/k (k為v的鄰居節點的度數)。最大化outwardness的復雜度為O(kd2log|B|),而對于稀疏網絡,則為O(k log|k|)[9]。 2) 子簇迭代合并算法(ICSC)的復雜度 ICSC算法中,每一步選擇長度最小的子簇,通過計算其與每一個鄰居子簇合并后網絡全局模塊性的變化值:ΔGlobalMod,搜索能最大化ΔglobalMod的合并單元。根據式(2),因為是一個常量,所以,ΔGlobalMod的計算可分解為3部分: 式中:Δvalue1、Δvalue2和Δvalue3的計算分別如式(3)~(5)所示。設參與合并的兩個子簇為Mj和Mk,Mj和Mk合并后產生的子簇為Mjk,根據公式,每一次合并僅需通過合并前的參數值重新計算子簇Mjk的wjk和wjkD。所以,每一次合并的復雜度為O(kd)。對于有k個節點的復雜網絡,ICSC算法的復雜度為O(k2d)。 綜上所述,LAICA算法的復雜度為O(k2d)。 為了驗證LAICA算法的有效性和可行性,使用Zachary空手道俱樂部網絡(Zachary karate club network)[15]、多學科網絡(multi-discipline network)[3]和美國大學足球聯盟網絡(American college football network)[16]等多個真實網絡進行聚簇實驗。文獻[17]提出范化互信息(normalized mutual information,NM I)計算聚簇所得社區結構和真實社區結構的相似程度,本文也采用NM I作為聚簇精度對LAICA算法進行了定量分析與評估。實驗采用兩種參數產生初始節點:并比較這兩種參數設置下LAICA的聚簇精度,其中:Dn0=0時所選擇的初始節點即為網絡中度數最高的節點。實驗所獲社區結構將與文獻[4]中算法所獲社區結構進行比較。 Zachary空手道俱樂部網絡[15]由34個節點和78條邊構成,其中:節點代表俱樂部成員、邊代表成員之間的社會交往。因意見分歧,俱樂部分裂成以俱樂部管理者和俱樂部教練為中心的兩個子俱樂部。此網絡標準社區結構的ME值為4.409 3,而文獻[4]中算法發現的最佳社區結構ME值為4.311 8。 表2 空手道俱樂部網絡的avgNM I統計 表2統計了采用不同的局部模塊性和全局模塊性聚簇空手道俱樂部網絡的平均NM I值(AvgNM I)。當Dn0=0時,ME和Modularity兩種全局模塊性中,LMe、LM和MM均分別獲得了完全一致的AvgNM I值,其中:ME的AvgNM I值為0.991 6,而Modularity的AvgNM I值僅為0.342 7。當時,不同的局部模塊性和全局模塊性的結合所獲AvgNM I值均高于90%。整體而言,在兩種初始節點選擇參數設置下,ME的聚簇精度高于Modularity。圖2為初始節點數從12到32,4種局部模塊性的AvgNM I曲線圖。 圖2 空手道俱樂部網絡不同初始節點數的AvgNM I 多學科網絡(multi-discipline network)[3]以節點表示期刊、邊表示引用關系。如果一個期刊的某篇論文引用了另一期刊的某篇論文,則構成了兩個期刊之間的一個引用關系。網絡包含4個領域:multidisciplinary physics、chem istry、bioloegy和ecology,每一個領域為一個社區。每一個領域選取10個期刊共40個期刊作為節點,期刊之間的189個引用關系作為邊。該網絡標準社區結構的ME值是4.635 0,但文獻中[4]算法發現的最佳社區結構的ME值為4.620 0。 表3 多學科網絡的AvgNM I統計 表3總結了初始節點個數由15逐一增加到40,兩種不同的初始節點參數設置下,算法結合不同的局部模塊性和全局模塊性對多學科網絡聚簇的AvgNM I值。對于多學科網絡數據顯示,Modularity的聚簇精度高于ME。對于Modularity和ME兩種全局模塊性,LMe、LM和MM這3種局部模塊性也分別獲得了完全一致的AvgNM I值。采用ME的LAICA算法在時聚簇精度明顯高于Dn0=0;而采用Modularity,則兩種不同的初始節點選擇策略的聚簇精度非常接近。圖3為時,初始節點數從12到40時,4種局部模塊性聚簇多學科網絡的AvgNM I曲線。 圖3 多學科網絡不同初始節點數的AvgNM I 美國大學足球聯盟網絡(American college football network)是根據2000年秋季常規賽季的比賽計劃構建[16],以節點表示球隊、邊表示兩個球隊之間常規賽季的一場比賽。 網絡共包含115個節點和613條邊。115個球隊分屬于12個聯合會(conference),因處于同一個聯合會的球隊間的比賽次數要多于不同聯合會的球隊間的比賽次數,每一個聯合會建模為一個真實網絡社區。文獻[4]中算法聚簇得到了一個包含10個簇的社區結構,其ME值為5.441 7。 表4 美國足球聯盟網絡的AvgNM I統計 表4為初始簇個數從20逐一增加到115,兩種不同初始節點選擇策略下,結合不同的局部模塊性和全局模塊性聚簇足球聯盟網絡聚簇的AvgNM I值。數據顯示對于該網絡,ME的聚簇精度高于Modularity。對于Modularity和ME兩種全局模塊性,LMe、LM和MM這3種局部模塊性也分別獲得了完全一致的AvgNM I值。使用ME的LAICA算法在兩種不同的初始節點選擇策略的聚簇精度明顯高于 圖4 美國大學足球聯盟網絡不同初始節點數的AvgNM I 實驗結果表明,LACIA算法的聚簇精度隨初始局部簇個數的增加而上升。當初始簇個數與網絡的節點個數完全一致時,LACIA算法等同于快速隨機遞歸搜索算法[1,4],即:所有節點同時參與聚簇。隨著初始簇個數的增加,LACIA算法準確率升高,但計算消耗也增大。要實現準確率與計算消耗之間的折衷,需要設置合理的初始簇個數。在4種局部模塊性評價標準中,OW的計算和維護相對簡單,卻獲得了相對較好的聚簇精度。任一真實網絡,在Dn0=0的初始節點選擇策略下,LMe、LM和MM獲得的聚簇精度完全一致,表明這3種局部模塊性雖使用不同的參數量化局部簇的簇內和簇外連接數,但因其均采用簇內連接與簇外連接之間的比值來表示局部模塊性,搜索局部簇時,這3種局部模塊性均聚合了與局部簇內部連接最緊密的節點,導致最后獲得的局部簇結構相同。 圖5 真實網絡度分布曲線圖 3個網絡節點的度分布(degree distribution)[18]如圖5a~圖5c所示,僅空手道俱樂部網絡嚴格遵循冪律發布(power law)[19],而美國大學足球聯盟網絡節點的度分布則完全違背冪律分布。空手道俱樂部網絡的聚簇,當Dn0=0時,其平均NM I值均超過0.99,實驗數據還顯示,初始節點數從16遞增至32,使用ME的LACIA算法均能100%準確地搜索到該網絡的標準社區結構。而對于美國大學足球聯盟網絡,LACIA算法的聚簇精度最低。所以,對于遵循冪律分布的網絡,使用ME的LACIA算法的聚簇精度最佳。 本文提出了基于局部聚簇的自動聚簇算法(LACIA)。LACIA算法的特點如下:1) 利用局部聚簇發現局部連接緊密的節點集,獲得聚簇粒度更大且具有一定聚簇精度的局部簇網絡結構,從而減少全局聚簇的計算消耗;2) 迭代合并局部簇網絡的聚簇單元,自動決定網絡簇數并精確分配節點。4種局部模塊性評價標準:local modularity[7]、outwardness[9]、modularityM[10]和LMetric[11],在LACIA算法中均顯示出較高的聚簇能力。前3者對3個真實網絡的聚簇結果基本一致,表明其聚簇能力相似。而Outwardness[9]僅考慮單個鄰居節點與簇內和簇外的連接差異,計算簡單,卻獲得了相對較高的聚簇精度。實驗數據也表明,對于遵循冪律分布的網絡,使用ME的LACIA算法具有最佳聚簇精度。LACIA算法聚簇多個真實網絡,節點分配準確率最高達99.72%,表明該算法能精確有效地聚簇復雜網絡。本文的下一步工作將對LACIA算法聚簇大型網絡進行深入的探測和研究。 [1] NEWMAN M E J. Fast algorithm for detecting community structure in networks[J]. Physical Review E, 2004, 69(6):066133. [2] NEWMAN M E J, GIRVAN M. Finding and evaluating community structure in networks[J]. Physical Review E,2004, 69(2): 026113. [3] ROSVALL M, BERGSTROM C. An information-theoretic framework for resolving community structure in complex networks[J]. Proceedings of the National Academy of Sciences, 2007, 104(18): 7327-7331. [4] ROSVALL M, AXELSSON D, BERGSTROM C T. The map equation[J]. Eur Phys Journal, Special Topics,2009(178): 13-23. [5] CHEN D, FU Y, SHANG M. A fast and efficient heuristic algorithm for detecting community structures in complex networks[J]. Physica A: Statistical Mechanics and its Applications, 2009, 388(13): 2741-2749. [6] XIANG B, CHEN E, ZHOU T. Finding community structure based on subgraph sim ilarity[J]. Studies in Computational Intelligence, 2009(207): 73-82. [7] CLAUSET A. Finding local community structure in networks[J]. Phys Rev E, 2005(72): 026132. [8] WAKITA K, TSURUM I T. Finding community structure in mega-scale social networks[C]//In www'07: Proceedings of the 16th International Conference on World Wide Web.Banff(CANADA). NewYork: ACM Press, 2007: 1275-1276 . [9] BAGROW J P. Evaluating local community methods in networks[J]. Journal of Statistical Mechanics, 2008(7):05001. [10] LUO F, WANG J Z, PROM ISLOW E. Exploring local community structures in large networks[C]//Proceedings of the 2006 IEEE/W IC/ACM International Conference on Web Intelligence. Hongkong, China: IEEE Computer Society Press, 2006. [11] CHEN J, ZA?ANE O R, GOEBEL R. Detecting communities in social networks using local information[C]//From Sociology to Computing in Social Networks:Thoeory, Foundation and Applications. New York:SPRINGER-VERLAG W IEN, 2010(1): 197- 214. [12] FORTUNATO S, BARTHLEMY M. Resolution lim it in community detection[J]. Proceedings of the National Academy of Sciences, 2007, 104(1): 36-41. [13] FREEMAN L. Centrality in social networks: conceptual clarification. social networks[M]. Lansanne: Elsevier sequoia S.A., 1979. [14] SHANNON C E. A mathematical theory of communication[J]. Bell System Technical Journal, 1948(27): 379-432, 623-656. [15] ZACHARY W W. An information flow model for conflict and fission in small groups[J]. Journal of Anthropological Research, 1977(33): 452-473. [16] GIRVAN M, NEWMAN M E J. Community structure in social and biological networks[J]. Proceedings of the National Academy of Sciences, 2002, 99(12): 7821-7826. [17] DANON L, DAZ-GUILERA A, DUCH J, et al. Comparing community structure identification[J]. Journal of Statistical Mechanics: Theory and Experiment, 2005(9): 09008. [18] ALBERT R, BARABáSI A L. Statistical mechanics of complex networks[J]. Reviews of Modern Physics, 2002,74(1): 47-97. [19] BARABáSI A L. Linked: the new science of networks[M].Cambridge, MA, USA: Perseus Publishing, 2002. 編 輯 蔣 曉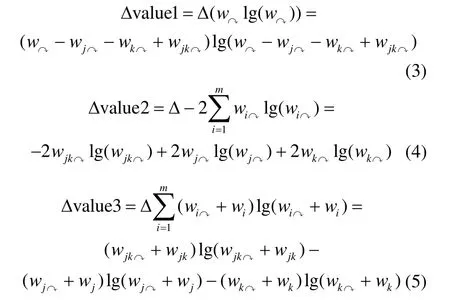
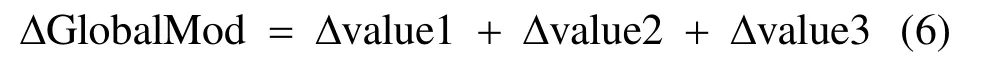
3 實 驗
3.1 Zachary空手道俱樂部網絡
3.2 多學科網絡
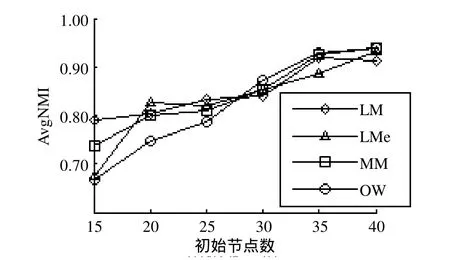
3.3 美國大學足球聯盟網絡
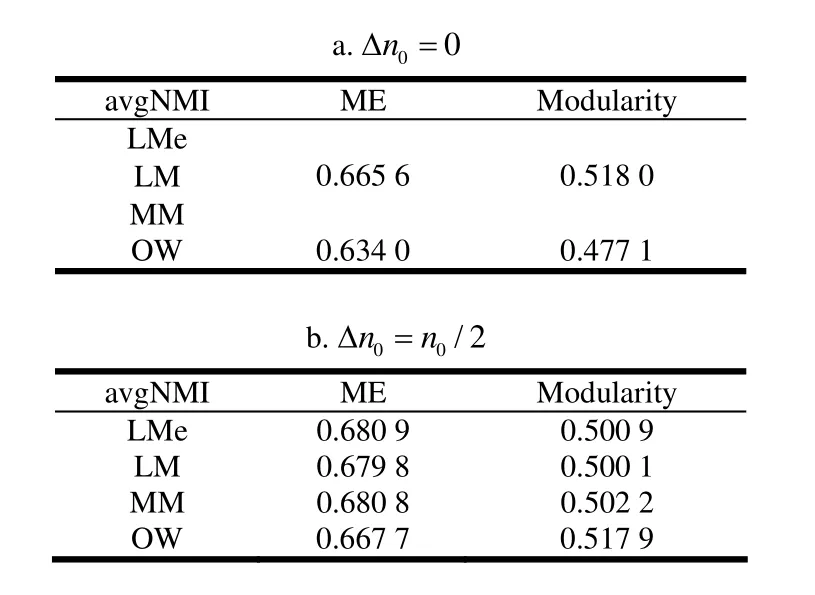
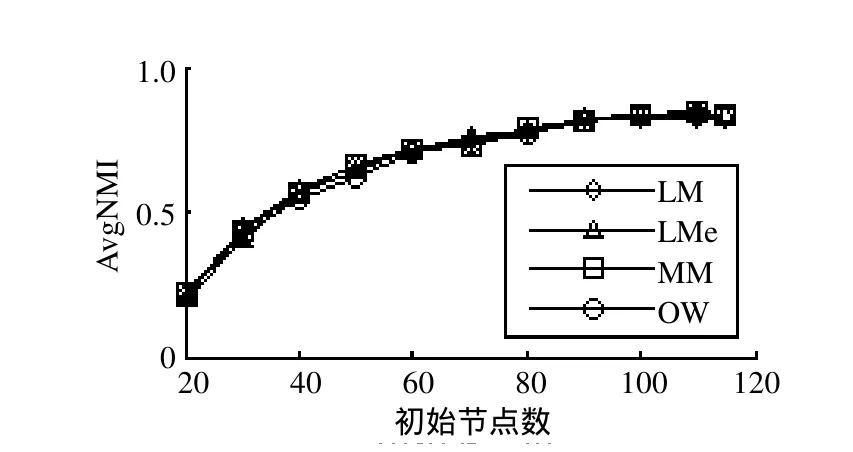
3.4 實驗結果分析
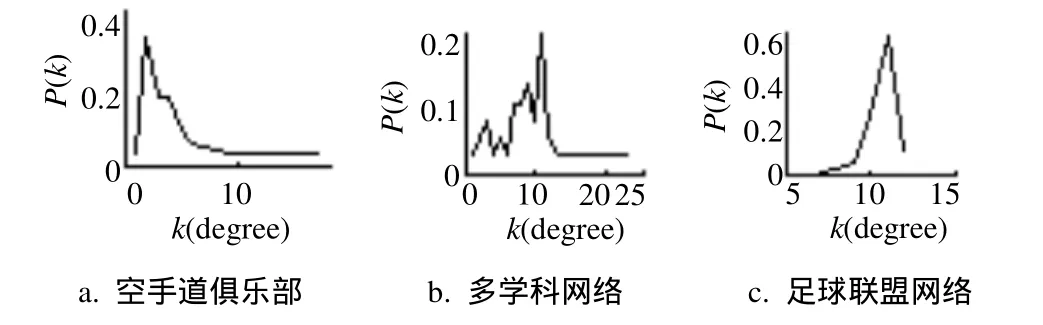
4 結論和未來工作

