一種改進的圖像邊緣提取算法

辛元芳

(安徽理工大學 電氣與信息工程學院，安徽 淮南232001)

責任編輯:任健男

1 邊緣檢測簡介

邊緣反映了圖像像素的不連續性，邊緣檢測的目標就是要能夠檢測出局部特征變化劇烈或者不連續的像素點，之后把這些像素點連接在一起構成物體的邊界。圖像的邊緣包含了很多有價值的邊界信息，這些信息對人們進行圖像分析與識別有著重大影響，廣泛應用于目標識別、計算機視覺、圖像分割和區域匹配等領域。尤為重要的是，邊緣具有一種相對不變性，光線變化可能會影響一個區域的外觀，但不會改變邊緣。因此，近年來，廣大學者對圖像邊緣檢測進行了大量研究。

對數字圖像檢測邊緣，通常是把待處理的圖像作為一個整體在空間域或者頻率域進行相應處理，常用的邊緣檢測算子包括Prewitt、Sobel和Robert等，它們都是通過檢測梯度的最大值來提取邊緣;Laplace算子則是檢測二階導數的零交叉點來提取邊界;這些算子引入了各種微分運算，其特點是計算起來比較簡單、容易實現，但是對含有噪圖像檢測的邊緣效果并不好，經常會丟失一部分邊緣細節并且會使噪聲加強，所以檢測到的邊緣并理想。近年來提出的Log和Canny等邊緣檢測算子，雖然效果有所改進，但計算量較大，實時性差[1]。后來人們又相繼將小波變換及數學形態學等理論引入了圖像處理中，開辟了邊緣檢測的新途徑[2]。

如喬鬧生等[3]結合小波變換模極大值的圖像邊緣檢測法及改進的灰值數學形態學圖像邊緣檢測兩種方法的優點，采用疊加運算進行圖像融合最終檢測到圖像邊緣。李杰等[4]基于數學形態學的圖像邊緣檢測算法的研究，提出了一種自適應邊緣檢測算法，用不同方向與尺寸的結構元素提取圖像邊緣。劉清等[5]將量子疊加態和信息熵相結合，構造出一種多結構的量子疊加態結構元素，此疊加態結構元素涵蓋線條的任意走向，從而檢測出完整、連續的邊緣，并在算法設計中利用圖像能量熵確定各疊加態結構元素的概率。但是因為只考慮了各個分量的自身能量分布，把各個分量之間的能量差別忽略了，無法根據熵值來區分圖像的噪聲和有效信號。趙晨等[6]將經驗模式分解用于邊緣檢測，對傳統的二維EMD方法進行了改進，將原始圖像分解為多個不同尺度的固有模態函數IMF(Intrinsic Mode Function)分量及一個余量之和，充分利用IMF1和IMF2分量的小尺度優勢，融合兩個方向上的邊緣以獲取最終的邊緣，但是效果一般，同時存在破壞了二維空間相關性的缺陷。

互信息來源于信息論，它是由熵的概念引申而來的。互信息體現了隨機變量之間相互包含的信息量及相互之間的統計依賴性。兩個隨機變量間的關聯性越強，其互信息就越大;反之，互信息就越小。若兩個隨機變量是相互獨立的，則互信息就是最小值零[7]。

因此，針對上述這些邊緣檢測方法在抑制噪聲、精確定位邊緣、較好地保留弱邊緣及圖像細節等方面的不足。本文結合BEMD分解和互信息熵及圖像疊加的優勢，將互信息與邊緣梯度特征有效融合，提出了一種改進的含噪圖像邊緣檢測算法。首先將圖像用二維EMD進行分解，利用相鄰分量間的互信息熵來衡量高頻部分與低頻部分的關聯強度。如果某個分量的互信息熵達到了之前設定好的拐點標準，那么就把該分量作為高頻與低頻的分界點。采用文獻[3]的方法對高頻分量用小波變換模極大值的圖像邊緣檢測法進行邊緣提取，低頻部分用數學形態學方法進行邊緣提取，最后，結合兩種方法的優點，采用疊加運算進行圖像融合最終檢測到圖像邊緣。該方法可以根據圖像信息的自身特性，將隱含在其中的各個模態依次剝離，通過圖像融合實現圖像信號的濾波、消噪，同時很好地保留邊緣圖像的細節特征。結果表明，該算法結合了邊緣比對方法的高效性和最大互信息方法的精確性，在有效保留邊緣的同時又較好地體現了原圖像的細節特征。

2 EMD分解

經驗模式分解(Empirieal Mode Decomposition，EMD)是N.E.Huang等人于1998年提出的一種全新的信號時頻分析方法;后來的學者不斷研究將一維EMD方法推廣到二維領域，即BEMD，并發現圖像能夠被BEMD分解為局部窄帶信號，這種應用潛力使得BEMD逐漸應用于圖像融合、邊緣檢測、圖像濾波等方面[8-9]。

現下流行的用來對時變頻率信號進行分析的小波分析等方法，大部分都采用了積分分析的方法，都是以傅里葉變換作為基本的理論依據，它們的基函數都是固定的，因此缺乏自適應性，不能精確描述頻率隨時間的變化。而EMD是一種非平穩、非線性信號時頻分析的新方法，其最大突破在于不依賴基函數，而是基于數據驅動的自適應分析方法，它將時間序列信號分解成一組含有不同尺度的固有模態函數IMF，不需要選擇基函數，同時具有多分辨率和自適應的特點[10]。

具體來說，EMD就是在時域的范圍內把復雜信號分解成一序列的基本內蘊模式函數(IMF)之和。要求每個本征模態函數符合下面兩個條件:

1)整個的數據段里極值點的個數必須和過零點的個數相等，最多只能相差一個。

2)任何時刻，局部的最大值與最小值點所定義的包絡線平均值必須為零。

經驗模式分解的基本思想就是對于給定的信號，先求得信號的極值，然后通過插值獲取信號的包絡及其平均值，再計算原數據與均值的差，分解得到一層信號，直到將信號分解成有限個本征模態函數IMF和殘差rn(t)的組合，分解過程可表示為

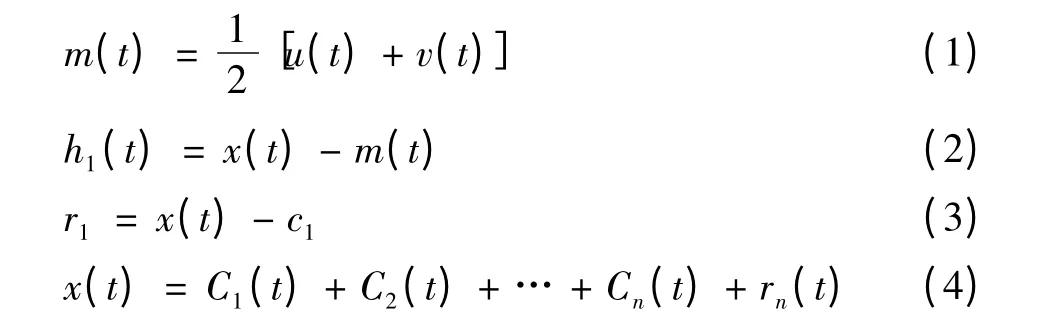
式中:rn為殘差函數，表示信號的平均趨勢。

在式(4)中若忽略rn(t)，則有

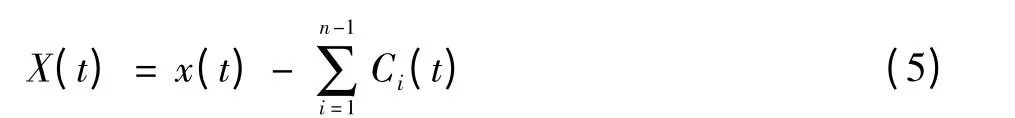
對灰度圖像而言，BEMD分解要首先在投影面上進行局部極大值點和極小值點的選取，并形成其所定義的包絡曲面，得到局部均值曲面，然后通過不斷地篩選，最終得到有限個二維固有模態分量BIMF和趨勢項。

由于二維EMD具有完全由數據驅動的自適應性，因此，在其逐步提取圖像局部高頻、次高頻的分解過程中，反映了人類在區分圖像不同紋理時視覺與頻率的相觀性。這使得BEMD在圖像邊緣提取時具有其獨特的優勢，在準確檢測出圖像邊緣的同時還能利用其數據驅動的自適應性有效抑制噪聲，性能上要比傳統的邊緣提取算法優越。而這其中能夠分離有效信號與噪聲的關鍵就是怎樣選擇重構分量。如果選擇了太多的重構分量，則大量噪聲無法去除;反之，如果選擇過少，又可能丟失有用的細節特征和邊緣信息。對圖像進行二維EMD分解得到不同分量IMF1，IMF2，…，IMFn，分別對每個IMF求其能量

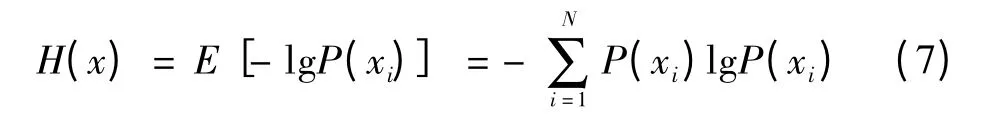
如果用互信息來描述BEMD分解后得到的相鄰分量能量熵之間的相關性，則可表示為

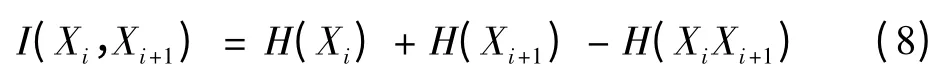
在二維EMD分解時，圖像信號從高頻到低頻依次分解，則式(4)可以寫為

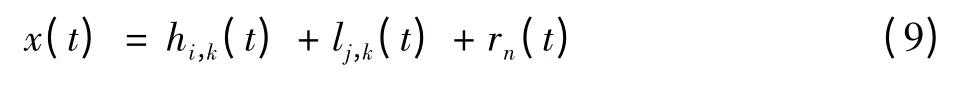
式中:i=1，2，…，k;j=k，k+1，…，n。假設高頻部分和低頻部分之間的相互統計是獨立的，那么由信息論可以知道:兩個隨機變量如果是相互獨立的，它們之間的互信息應該等于零。相鄰的本征模態函數分量間的互信息值將在高頻到低頻之間出現由大到小再到大的過程，在這過程中勢必會出現一個轉折點。利用該特點，由互信息原則，能夠找到高頻與低頻之間的轉折點，從而得到如下目標函數

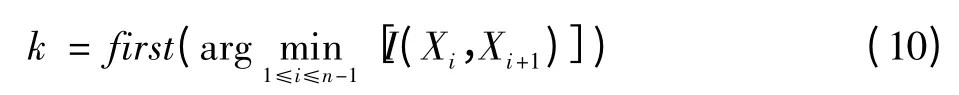
如果將高頻分量直接舍棄，會損失存在于其中的有用信息，并且達不到降噪效果。因此這里采用文獻[3]的方法分別對分界后的低頻近似子圖像fL用改進的灰值數學形態學進行邊緣檢測得到其邊緣fLe，對高頻細節子圖像fH用小波模極大值法抑止噪聲進行邊緣檢測得到其邊緣fHe。

3 圖像邊緣提取算法

綜上所述，基于BEMD和互信息熵的圖像邊緣提取的具體過程如下:

1)用BEMD分解含噪聲的源圖像f(x，y)，得出各個不同的BIMF分量;

2)由式(7)和式(8)計算得到各個分量的能量熵;

3)按照式(9)計算各分量能量熵之間的互信息;

4)按照式(10)找到高頻與低頻之間的轉折點;

5)由步驟4)得出轉折點后，采用文獻[3]的方法分別對低頻近似子圖像和高頻細節子圖像進行邊緣檢測。最后將兩者采用疊加運算進行圖像融合即可得

4 算法驗證

本文在MATLAB7.5環境下對該算法進行了驗證，如圖1所示，傳統的數學形態學算法雖然被檢出的邊緣分辨率較高，但對噪聲抑制效果不佳;基于小波的邊緣提取算法圖像邊緣不夠連續;文獻[3]結合小波變換模極大值及改進的灰值數學形態學圖像邊緣檢測兩種方法的特點，雖然消除了大部分噪聲，但無法保留邊緣細節。與文獻[3]的圖1e對比可知，圖1f在去除噪聲的同時最大限度地保留了圖像的邊緣特征。

圖1 邊緣圖像

由以上分析可知，本文結合BEMD分解和互信息熵確定高頻和低頻部分的分界，充分利用BEMD的自適應多分辨特性，與小波降噪方法相比較，該方法不需要對基函數與分解層數進行選取，其降噪處理的過程完全是取決于信號特征的自適應降噪。該算法結合了邊緣比對方法的高效性和最大互信息方法的精確性，在有效保留邊緣的同時又較好地體現了原圖像的細節特征。實驗結果表明，同傳統方法相比，這種改進的邊緣檢測方法在有效提取出圖像邊緣細節的同時抑制了噪聲，準確度較高，細節信息保留較多，但又不會檢測出過多的邊緣，為圖像后續處理提供了一個很好的基礎。

[1]JIANG J A，CHUANG C L，LU Y L，et al.Mathematical-morphologybased edge detectors for detection of thin edges in low-contrast regions[J].IET Image Processing，2010，1(3):269-277.

[2]ZHAO Yuqian，GUI weihua，CHEN Zhencheng.Edge detection based on multi-structure elements morphology[C]//Proc.IEEE 6th World Congression Intelligent Control and Automation.Dalian:IEEE Press，2009:9795-9798.

[3]喬鬧生，鄒北驥，鄧磊，等.一種基于圖像融合的含噪圖像邊緣檢測方法[J].光電子·激光，2012，11(23):2215-2220.

[4]李杰，苗長云，武志剛，等.基于數學形態學的圖像邊緣檢測算法的研究[J].計算機科學，2012，6(39):546-547.

[5]劉清，曾小薈，王忠華，等.量子疊加態和信息熵的形態邊緣提取算法[J].計算機應用研究，2012，6(29):2387-2389.

[6]趙晨，周振國，崔穎.基于二維EMD改進方法的圖像邊緣檢測[J].黑龍江大學工程學報，2012，3(3):106-110.

[7]GAO C B，ZHOU J L，HU J R，et al.Edge detection of colour image based on quaternion Fractional differential[J].IET Image Processing，2011，5(3):261-272.

[8]林麗，周霆.HHT在眼底圖像邊緣檢測中的應用[J].通信技術，2011，11(44):71-75.

[9]NORDEN E，SHEN Z，STEVEN R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time analysis[C]//Proc.the Royal Society of London，Series A.London:[s.n.]，1998:903-995.

[10]ZHANG Xin，SUN Fuchun.Pulse coupled neural networkedge-based algorithm for image text locating[J].Tsinghua Science and Technology，2011，16(1):22-30.