多晶鐵沖擊相變的離散元方法研究

劉超，石藝娜，秦承森，梁仙紅

(北京應用物理與計算數學研究所，北京100088)

0 引言

沖擊相變是當前沖擊波與爆轟物理研究領域的熱點問題之一，由于其對于高溫高壓極端條件下材料物性研究的科學意義及在高新技術領域的應用背景，沖擊相變研究受到廣泛關注。同時，沖擊相變還是一個非線性、非平衡的復雜物理過程，具有時間相關效應;并且沖擊相變研究既是一個涉及物理、力學、材料科學及冶金學的交叉學科問題，又是一個典型的多個尺度問題。因此，沖擊相變也是沖擊波物理研究的難點問題之一。自1956 年Bancroft 等采用炸藥加載首次觀察到鐵的沖擊相變［1］以來，眾多研究者在沖擊相變領域積累了豐富的文獻資料，同時也發現了許多有趣的實驗現象。

時至今日，沖擊相變研究仍集中于實驗和唯象理論模型方面，對于其細觀機理研究相對較少，其中一個很重要的原因是缺乏細觀尺度數值模擬手段。盡管多尺度算法研究發展十分迅猛，但多集中于宏觀尺度計算方法與分子動力學等微觀尺度算法耦合的搭橋類算法，細觀尺度的計算方法很少。目前，研究多晶材料沖擊響應的細觀尺度數值模擬方法，原則上可分為兩類:一類是以離散元為代表的粒子類方法，另一類是以連續介質力學為基礎的傳統數值模擬方法。與傳統數值模擬方法相比，離散元具有模型構建方法易行、晶粒間各相異性特性表征便捷、算法實現簡單等優點。

離散元法是20 世紀70 年代初由美國學者cundall 首先提出的［2］，最初主要應用于巖石力學、顆粒態群體及土壤力學問題分析中。離散元方法允許單元間的相對運動，而且不象連續介質模型那樣的依賴于高度簡化、規定性的本構關系，并具有算法簡單、易于實現的優點。20 世紀90 年代初，Sawamoto等［3］首先將離散元方法成功地用于混凝土動態沖擊破壞等非線性大變形問題的數值模擬研究。劉凱欣等在這一領域做了大量的研究工作［4-5］。1999年以來，Yano 等［6］、Case 等7］利用離散元方法研究了銅、鐵等多晶金屬的沖擊響應。2000 年以后，王文強［8］、于繼東等［9］將離散元方法應用到非均質材料炸藥在沖擊作用下細觀損傷的研究。這些工作展示了離散元方法模擬細觀非均質材料動力學問題的能力。由于可以方便地表征晶粒間取向的分布特征，離散元方法在模擬細觀非均質材料的沖擊響應方面具有獨特的優勢。

本文利用離散元方法結合基于無擴散相變的兩相模型，對于α 鐵的沖擊相變過程進行了數值模擬研究，給出了鐵的相邊界及沖擊Hugoniot 關系。并在此基礎上對于多晶鐵的沖擊相變過程進行了模擬，研究了晶粒大小及傳播距離對于沖擊波前沿不規則度的影響，并對沖擊相變過程中相變特征量隨局部沖擊壓力的變化規律進行了統計。

1 計算方法與相變模型

離散元方法通過求解多體運動的牛頓力學方程組，跟蹤全部單元的運動軌跡，來揭示系統與外界的相互作用和自身響應、演化規律。與傳統的數值模擬方法相比，離散元具有處理沖擊載荷作用下單元間常見的大變形、斷裂等問題方便，算法實現簡單等優點。

1.1 單元間相互作用力模型

一般單元間可能包括以下相互作用力［10］:1)中心勢力;2)中心阻尼;3)彈塑性剪切力;4)切向阻尼;5)干摩擦力。如圖1 所示，圖中v 為線速度，ω為角速度。

圖1 單元間相互作用力的示意圖Fig.1 Interaction model of an element-pair

利用圖1 描述的單元間相互作用力模型，可將單元i 與j 間的作用力合力表示為

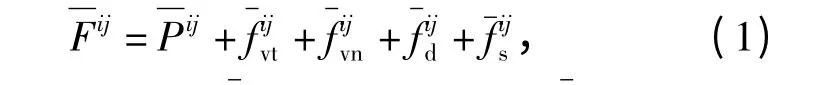
根據所研究的問題選取合適的單元間作用力模型是離散元方法研究的核心內容，本文采用適合于描述材料沖擊響應的單元間作用力模型，模型中單元間相互作用力主要包括中心勢力與中心阻尼，兩相單元間相互作用力模型參數取值見文獻［11］。

1.2 溫度與相變模型

影響單元溫度的力學過程可以分為可逆過程與不可逆過程，可逆的力學過程如中心勢力的作用過程，不可逆的力學過程為耗散力的作用過程［11］:

采取與Forbes［12］類似的推導方法，可以得到溫度的可逆部分，即等熵過程中溫度可表示為

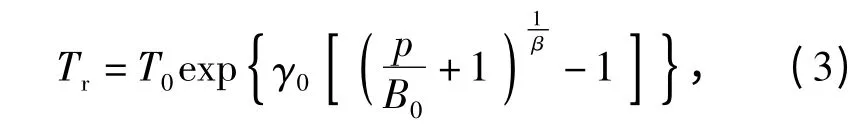
式中:T0為初始溫度;p 為靜水壓力;B0與等溫體模量KT相關，B0= KT/β，β 為狀態方程參數;γ0為Gruneisen 參數。

不可逆部分僅考慮了由熱傳導和粘性力帶來的能量耗散過程，不可逆過程帶來的溫升是上述兩類過程的累計效應:

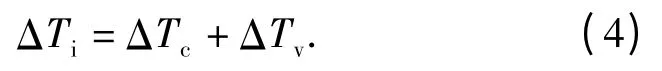
連接與接觸單元間考慮了基于傅里葉定律的熱傳導過程:

式中:ΔQ 為在Δt 時間內由單元j 向單元i 傳導的熱;κ 為熱傳導系數;Ti和Tj分別為單元i 與單元j的溫度;dij為單元i 與單元j 間的距離;Aij為單元i與單元j 間的接觸面積。

由熱傳導導致的單元溫度變化，可表示為

由粘性力帶來的溫升:

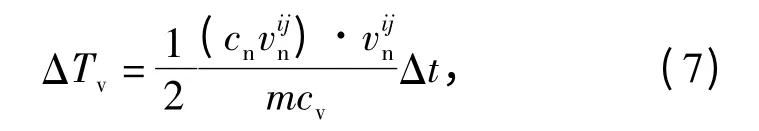
式中:m 為單元質量;cv為等容比熱;Cn為粘性系數為單元i 與單元j 間的相對速度在其中心連線方向的投影。

本文采用基于無擴散相變的兩相模型，該模型基于如下假設:1)每個單元中的相變均勻產生，并由局部能量條件控制;2)單元中的壓力和溫度滿足局部平衡條件。相變模型包括3 個重要的組成部分:1)平衡的相邊界;2)局部閾值條件;3)相變動力學方程。

首先，平衡的相邊界，即相邊界處兩相的Gibbs自由能相等Gα(p，T)= Gε(p，T)). 此處i 相的Gibbs 自由能的表達式為

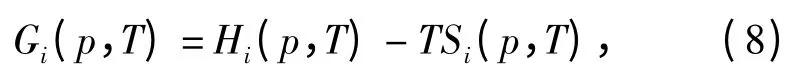
式中:Hi和Si分別為比焓與熵，下標i 分別表示α與ε 相。

在壓力不太高的情況下，沖擊壓縮產生的熵增不大，等熵過程與沖擊壓縮過程差別不大。因此，對于本文所研究的壓力范圍內，可采用Murnaghan 狀態方程，并采取與Forbes［12］類似的推導方法，得到以下比焓與熵的表達式:

式中:下標0 為初始狀態;V0i為零壓下的比體積;具體溫度及相變模型參數取值見表1.

表1 溫度及相變模型參數Tab.1 Values of temperature and phase transition model parameters

其次，局部閾值條件，即當自由能差額ΔG=Gα-Gε超過某一閾值時相變立即被觸發。計算中相變和逆相變的激活能分別為ΔGf和ΔGb.

再次，相變動力學方程，用于描述相變份額λE的變化率，本文分別采用1 階與2 階動力學方程，具體形式如下:

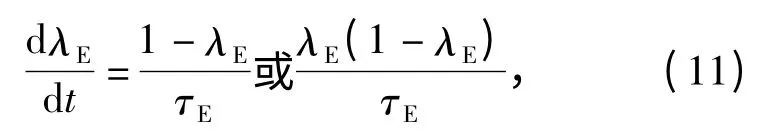
式中:λE為單元中ε 相的質量份額;1 階相變動力學方程中λE∈［0，1］，初始時刻取λE=0;2 階相變動力學方程中λE∈［0.001，0.999］，初始取λE=0.001;τE為單元相變松弛時間，由單元直徑與馬氏體相變速率之比進行估算，文中相變速率近似取常數1 km/s.

α-ε 相變伴隨著約5%的體積變化，數值模擬中通過依據單元中ε 相的質量份額改變單元半徑來模擬這一效應:

式中:r0為單元初始半徑;V0α、V0ε分別為零壓狀況下a 和ε 相的比體積。

本文在計算中僅考慮了靜水壓力而未考慮偏應力對于相變過程的影響。

2 α 鐵的數值模擬結果與分析

計算模型飛片與靶板均為6 400 μm×27 μm 的α 鐵，單元直徑為9 μm，計算單元總數約5 000 個。如圖2 所示，計算模型的上、下邊界采用周期性邊界條件，左、右邊界采用自由邊界條件。初始溫度300 K，飛片不同的速度從左端撞擊靶板。

圖3 給出了準靜態加載條件下鐵的相圖。從圖3 可以看出，本文計算結果與文獻［16 -19］實驗結果符合較好，證明本文采用的無擴散兩相模型能夠正確反應α 鐵的相變特性。

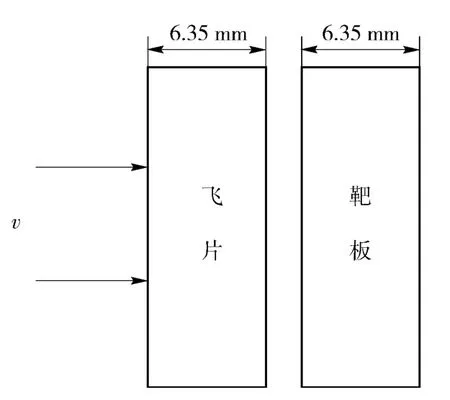
圖2 計算模型示意圖Fig.2 Initial model

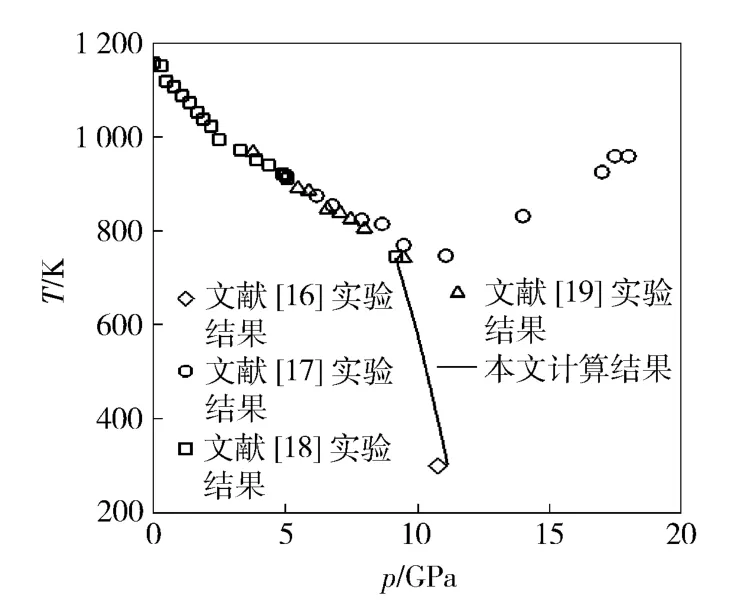
圖3 準靜態加載條件下鐵的相圖Fig.3 Phase diagram of iron under quasi-static loading

數值模擬結果顯示室溫300 K 下平衡態相邊界通過11.15 GPa 壓力點。Barker 等［20］通過實驗發現鐵的沖擊相變壓力閾值在(12.9 GPa，13.7 GPa)范圍內，逆相變壓力閾值在(9.4 GPa，10.2 GPa)范圍內。因此，文中取相變的激活能為13.40 J/g，對應室溫條件下相變的臨界壓力13.37 GPa;逆相變的激活能取為-8.24 J/g，對應室溫條件下逆相變的臨界壓力為9.80 GPa.

圖4(a)給出了Fe 的p-V/V0Hugonoit 曲線;圖4(b)給出了Fe 的沖擊波波速D 與波后粒子速度up的關系圖。由圖4 可以看出，本文計算結果與文獻［1，20 -21］實驗結果符合較好，證明計算所用單元間作用力模型及相變模型能夠正確反應鐵的沖擊壓縮及相變特性。

此外，圖4(a)的模擬結果顯示，沖擊相變壓力閾值約12.95 GPa，比室溫下的結果13.37 GPa 低了約0.42 GPa，這說明沖擊導致靶板內溫度升高，從而致使相變的壓力閾值降低。圖4(b)結果表明:當沖擊壓力小于相變壓力閾值時，樣品內波形為單波結構;當沖擊壓力在相變壓力閾值至約36 GPa 之間，波形為雙波結構(沖擊波與相變波);當沖擊壓力繼續增大時，相變波與沖擊波匯合成穩定的沖擊波。當沖擊壓力低于相變壓力閾值時，沖擊波速度隨波后粒子速度近似呈線性增長;當沖擊壓力高于相變壓力閾值時沖擊波近似以定常速度傳播，而相變波波速隨波后粒子速度增加較快。

圖4 鐵的沖擊Hugoniot 關系Fig.4 Hugoniot data of Iron

3 多晶鐵的數值模擬結果與分析

沖擊壓縮過程中多晶金屬，在晶粒尺度上是一個各向異性、非平衡過程，此時的沖擊波結構不能為傳統的連續介質力學描述［22］。Meyers 和Carvalho應用晶粒取向的概然論模型研究了多晶鎳的沖擊響應，結果表明傳入多晶中的沖擊波前沿變得不規則，其波面不規則度與晶粒尺寸同量級［23］。本文構建了兩種不同晶粒尺度的多晶鐵模型(如圖5)，采用離散元方法研究了晶粒尺度對于沖擊波波面不規則程度的影響。

圖5 兩種不同晶粒尺度多晶鐵模型局部放大示意圖Fig.5 Enlarged view of initial model of polycrystalline iron

多晶鐵模型中的晶粒取向呈隨機分布，以此表征晶粒間取向的分布差異。各晶粒的取向為(0° ～60°)之間的隨機數，晶粒內部單元為規則的密排六邊形，晶界處的間隙由小尺度單元填滿，圖5 中不同灰度代表不同晶粒取向，兩種模型的具體參數參見表2 所示。為避免邊界效應的影響，計算模型的上、下邊界為周期型邊界條件，左側為固壁邊界，右側為自由邊界，初始時刻模型以一定的速度撞擊固壁。

表2 兩種晶粒尺度多晶鐵模型參數Tab.2 Parameters of polycrystalline iron models

圖6 為兩種不同晶粒大小的多晶鐵以700 m/s的速度撞擊固璧后，某時刻模型中的沖擊波前沿位置圖。此處，定義波后粒子速度等于0.5 倍撞擊速度的位置為沖擊波前沿位置，圖中深色部分為沖擊壓縮區，淺色部分為未受沖擊區域。數值模擬結果表明，沖擊波前沿分布并不均勻，并且大晶粒模型內沖擊波前沿的不規則程度更高。

圖7 為沖擊波前沿位置中線定義示意圖，圖中的黑色粗實線代表沖擊波前沿位置，陰影部分為波后的沖擊壓縮區。如圖7 所示，沿y 向在沖擊波輪廓線的波峰(y 向最大值)與波谷(y 向最小值)之間選取一條直線(平行于x 軸)，使得直線上方的陰影面積之和等于直線下方的空白面積之和，并定義該直線位置為沖擊波前沿位置中線。

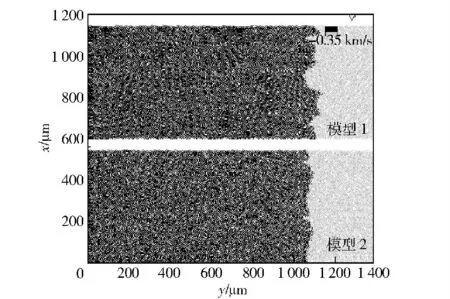
圖6 兩種不同晶粒尺度多晶鐵中的沖擊波前沿位置Fig.6 The shock wave front in polycrystalline iron

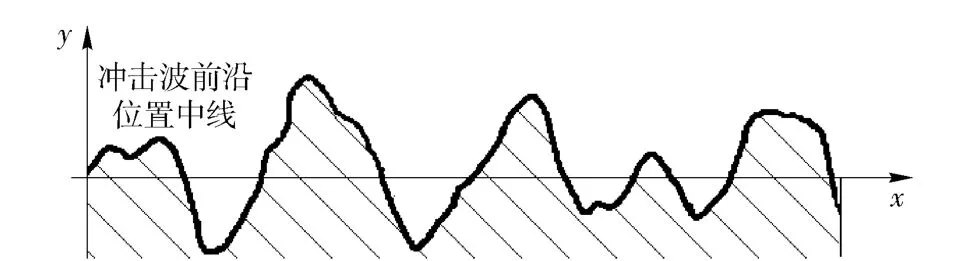
圖7 沖擊波前沿位置中線的定義Fig.7 The definition of shock wave front midline

統計不同時刻兩種不同晶粒大小的多晶鐵模型中，沖擊波前沿位置距離中線位置的標準偏差。圖8 給出了沖擊波前沿位置的標準偏差隨沖擊波傳播距離的變化關系。從統計結果看，沖擊波的波面不規則程度隨傳播距離的增加而增加;晶粒大小對于沖擊波前沿的不規則程度有一定影響，大晶粒模型內沖擊波前沿的不規則程度更高。

圖8 沖擊波前沿位置的標準偏差隨沖擊波傳播距離的變化Fig.8 Variation of standard deviation in the shock wave front position

圖9為模型1 以600 m/s 速度撞擊固壁后，沖擊波前沿附近的質量份額與壓力圖，圖中Ve 代表相變質量份額，p 為壓力。從圖可以看到:由于晶粒間取向分布差異及晶粒邊界效應的影響，壓力及質量份額場的分布很不均勻，應力遠高于或低于波后平均應力的區域集中于晶界附近;從沖擊波前沿位置可見，由于應力集中效應的影響，相變首先發生在晶界處，然后穿透到晶粒內部;在沖擊波前沿處的一些晶粒中，可觀察到指狀傳播的相邊界。

圖9 沖擊波前沿附近的質量份額與壓力Fig.9 Transformed mass fraction and pressure fields

室溫下靜壓實驗的測量結果表明，即使在準靜態條件下，鐵的α→ε 相變也并非沿平衡面進行［24］。Boettger 等的理論計算結果表明，沖擊相變過程中得到的p-λ 曲線與靜壓實驗的測量結果非常相近［25］。本文采用寬度27 μm 的采樣窗，沿著波的傳播方向統計相變質量份額與局部平均壓力。

圖10 為采用以上統計方法得到的局部平均壓力與相變質量份額曲線。圖中的離散點為靜壓實驗的測量結果［24］，兩條曲線分別為采用1 階與2 階動力學方程得到的統計結果。從圖10 中可見，沖擊相變的局部壓力-相變質量份額曲線均逐漸逼近準靜態壓縮實驗曲線上的點。本文的統計結果與Boettger 等［25］的結果可以互相佐證。采用兩種動力學方程得到結果的重要不同點在于相變臨界壓力，1 階模型的相變臨界壓力約為8 GPa，2 階模型的相變臨界壓力為10 GPa;與1 階動力學方程的統計結果相比，2 階動力學方程得到的局部平均壓力-相變質量分額曲線在低壓段(小于13 GPa)，與實驗結果符合更好。

4 結論

本文利用離散元方法，結合基于無擴散相變的兩相模型，模擬了α 鐵的沖擊相變過程，數值模擬結果表明:

1)計算得到鐵的相邊界、沖擊Hugoniot 關系與實驗結果符合較好，證實采用離散元方法結合兩相模型模擬α 鐵沖擊相變過程是可行的。

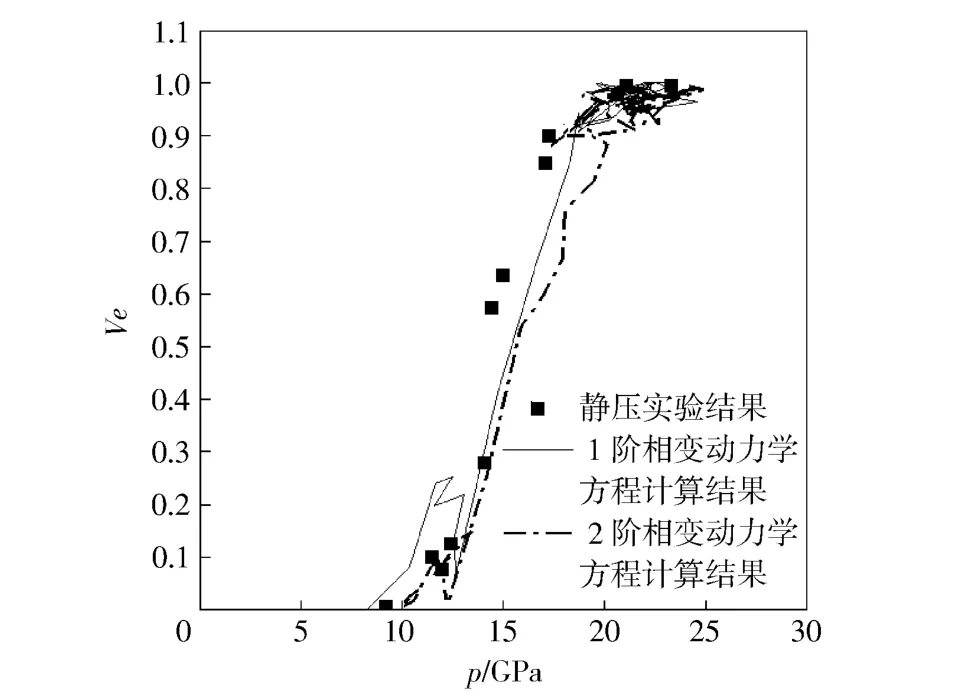
圖10 局部平均壓力與相變質量份額Fig.10 Local average pressure and transformed mass fraction

2)對多晶鐵的沖擊響應過程進行了模擬，初步的數值模擬結果顯示沖擊波的波面不規則程度隨傳播距離的增加而增加，大晶粒模型內沖擊波前沿的不規則程度更高。

3)對多晶鐵沖擊相變過程進行了統計，結果表明沖擊相變的局部壓力-相變質量份額曲線均逐漸逼近準靜態壓縮實驗曲線上的點;與1 階動力學方程的相比，2 階動力學方程得到的局部平均壓力-相變質量分額曲線在低壓段與實驗結果符合更好。

References)

［1］Bancroft D，Peterson E L，Minshall S. Polymorphism of iron at high pressure［J］. J Appl Phys，1956，27(3):291 -298.

［2］Cundall P A. A computer model for simulating progressive large scale movement in block rock system［C］∥Symposium ISRM.Nancy，France:International Society of Rock Mechnics，1971:129 -136.

［3］Sawamoto Y，Tsubota H，Kasai Y，et al. Analytical studies on local damage to reinforced concrete structures under impact loading by discrete element method ［J］. Nucl Eng Des，1998，179:157 -177.

［4］劉凱欣，高凌天，鄭文剛. 混凝土動態破壞過程的數值模擬［J］. 工程力學，2000(增刊):470 -474.LIU Kai-xin，GAO Ling-tian，ZHENG Wen-gang. Numerical simulation for the concrete failure process under shock loading［J］.Engineering Mechanics，2000(Suppl)470 -474. (in Chinese)

［5］劉凱欣，高凌天. 離散元法在求解三維沖擊動力學問題中的應用［J］. 固體力學學報，2004，25(2):181 -185.LIU Kai-xin，GAO Ling-tian. The application of discrete element method in solving three-dimensional impact dynamics problems［J］. Acta Mechanica Solida Sinica，2004，25(2):181 -185.(in Chinese)

［6］Yano K，Horie Y. Discrete-element modeling of shock compression of polycrystalline copper ［J］. Phys Rev B，1999，59:13672 -13680.

［7］Case S，Horie Y. Mesomechanics of the α-δ transition in iron［J］. J Mech Phys Solids，2007，55:589 -614.

［8］王文強. 離散元方法及其在材料和結構力學響應分析中的應用［D］. 合肥. 中國科學技術大學，2000.WANG Wen-qiang. Discrete element method and its use in analysis of response of materials and structures［D］. Hefei:University of Science and Technology of China，2000. (in Chinese)

［9］于繼東，王文強，劉倉理，等. 炸藥沖擊響應的二維細觀離散元模擬［J］. 爆炸與沖擊，2008，28(6):488 -493.YU Ji-dong，WANG Wen-qiang，LIU Cang-li，et al. Two-dimensional mesoscale discrete element simulation of shock response of explosives［J］. Explosion and Shock Waves，2008，28(6):488 -493. (in Chinese)

［10］Tang Z P，Horie Y，Psakhie S G. Discrete meso-element modeling of shock processes in powders［C］∥High Pressure Shock Compression of Solids Ⅳ，Response of Highly Porous Solid to Shock Loading. N Y:Springer，1997:143 -176.

［11］Yano K，Horie Y. Mesomechanics of the α-ε transition in iron［J］. International Journal of Plasticity，2002，18:1427 -1446.

［12］Forbes J W. Experimental investigation of the kinetics of the shock-induced alpha to epsilon phase transformation in armco iron，WSU-SDL 76-01［R］. Pullman，Washington:Washington State University，1976:112 -120.

［13］Anderson O L. Equations of state of solids for geophysics and ceramic science［M］. New York:Oxford University，1995:195.

［14］Lide D R，Kehiaian H V. CRC handbook of thermophysical and thermodynamical data［M］. US:CRC，1994:136.

［15］Jephcoat A P，Mao H K，Bell P M. The static compression of iron to 78 GPa with rare gas solids as pressure-transmitting media［J］. J Geophys Res，1986，91:4677 -4684.

［16］Giles P M，Longenbach M H，Marder A R. High-pressure α-ε martensitic transformation in iron ［J］. J Appl Phys，1971，42(11):4290 -4295.

［17］Bundy F P. Pressure-temperature phase diagram of iron to 200 kbar，900 ℃［J］. J Appl Phys，1965，36(2):616 -620.

［18］Kennedy G C，Newton R C. Solids under pressure［M］. New York，McGrawHill，1963:163.

［19］Clougherty E V，Kaufman L. High pressure measurement［M］.Washington，Giadini A A，Lloyd E C，1963:152.

［20］Barker L M，Hollenbach R E，Shock wave study of the αTMε phase transition in iron［J］. J Appl Phys，1974，45:4872 -4887.

［21］Brown J M，Fritz J N，Hixson R S. Hugoniot data for iron［J］.J Appl Phys，2000，88:5496 -5498.

［22］Wallace D C. Irreversible thermodynamics of flow in solids［J］.Phys Rev B，1980，22(4):1477 -1486.

［23］Meyers M A ，Carvalho M S. Shock-front irregularities in polycrystalline metals［J］. Mater Sci Eng，1976，24:131 -135.

［24］Taylor R D，Pasternak M P，Jeanloz R. Hysteresis in the high pressure transformation of bcc-to hcp-iron ［J］. J Appl Phys，1991，69(8):6126 -6128.

［25］Boettger J C，Wallace D C. Metastability and dynamics of the shock-induced phase transition in iron［J］. Phys Rev B，1997，55:2840 -2849.