雷達板級雙應力交叉步降加速退化試驗優化設計

潘 剛，梁玉英，呂 萌，張國龍，李 偉，孟 軍

（軍械工程學院，河北 石家莊 050003）

雷達板級雙應力交叉步降加速退化試驗優化設計

潘 剛，梁玉英，呂 萌，張國龍，李 偉，孟 軍

（軍械工程學院，河北 石家莊 050003）

針對某型雷達板級的性能往往受到多個應力的影響，且在加速退化試驗中該產品有限試驗時間內難以獲得大量性能退化信息的問題，提出一種雷達板級雙應力交叉步降加速退化試驗優化設計方法。采用Monte-Carlo對加速試驗進行仿真模擬，在樣本量大小一定的條件下，以監測頻率、應力水平數、監測次數作為設計變量，以總的試驗費用作為約束條件，以正常使用應力下的p階分位壽命漸進方差估計作為目標函數，建立下雙應力交叉步降加速退化試驗優化設計模型。通過仿真實例，驗證了該方法的有效性、可行性。

雷達；性能退化；雙應力步降加速退化試驗；優化設計

0 引言

傳統加速退化試驗優化設計大都針對失效機理明確、特征量易于測量、退化失效建模的簡單電子器件進行分析。Shuo-Jye Wu[1]、Jing-Rui Zhang[2]和Chen-Mao Liao[3]以費用作為約束條件分別對傳退化試驗及布朗運動模型和隨機過程分布下步階加速退化試驗的優化設計進行研究。LC Tang等[4]以正常使用應力水平下平均壽命漸進方差作為約束，以試驗費用最少為目標，對隨機過程分布下的步進加速退化試驗設計方法進行了研究。Zheng-zheng Ge等[5]在試驗截尾時間和樣本量大小的約束下，以正常使用應力下的p階分位壽命可靠度漸進方差估計為目標，對布朗運動模型下步進加速退化試驗優化設計進行了研究。Xiao-yang Li等[6]對競爭失效模型下的步降加速退化試驗優化設計進行了研究。潘正強等[7]對基于Wiener過程的多應力加速退化試驗設計進行了研

究，而對于組成器件級的功能電路或電子系統的優化設計研究則相對較少，對功能電路的試驗優化問題，沒有較為完善的理論支持。故本文將采用Monte-Carlo仿真的方法對某型雷達板級的雙應力步降加速退化試驗進行模擬，在樣本給定條件下以費用作為約束，對混合效應模型下某型雷達板級的雙應力步降加速退化試驗進行分析。

1 雷達板級的雙應力步降加速退化試驗方法

1.1 試驗研究對象及試驗系統

試驗系統由溫/濕度環境控制設備、電源模塊及PXI試驗數據采集設備組成。以PXIS-2558T機箱作為數據采集系統主機箱，內置PXI-3800主控制器、PXI-5114、1*16多路開關Pickering40-657-001-4/16/1、1*4射頻多路開關Pickering40-749。主機箱以PXI總線與各模塊相連接，共用開關模塊，4NIC-X240線性電源為可靠性試驗系統提供電應力環境。

1.2 試驗步驟

參照文獻[2]可對雙應力交叉步降加速退化試驗步驟作如下具體描述。設有兩組應力水平S1和S2，每組應力組合包含一系列應力水平，為了后續方便分析，在此假定兩組應力水平數及應力組合數大小均為k。

在滿足上述假設的前提下對試驗過程具體描述如下：

在試驗樣本大小n一定的條件下，首先給出k個監測周期T1，T2，T3，…，Tk；其次將選取的樣本置于最高應力水平組合下監測T1小時；然后將放入下組應力水平組合下監測T2小時；如此試驗下去，直到最后一組應力水平組合（其中Ti就是應力組合水平持續的時間。整個試驗的應力施加過程如圖1所示。

2 模型假設

2.1 退化模型假設

假設在第i個應力組合下樣本的退化軌跡可用以下混合效應模型描述：

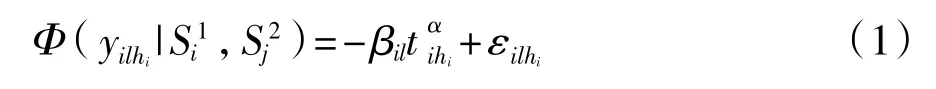
其中i=1，2，…，k；j=1，2，…，k；l=1，2，…，n；hi=1，2，…，mi。

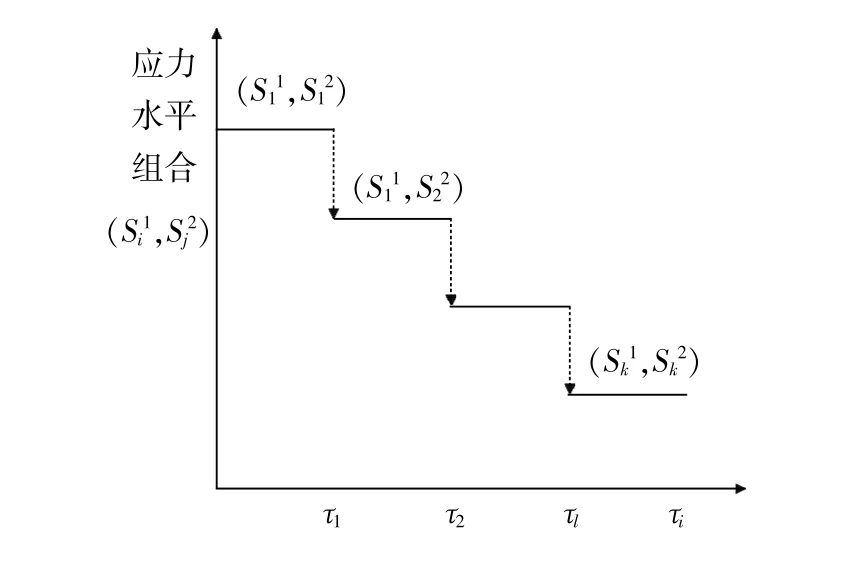
圖1 雷達板級雙應力步降加速退化試驗的應力施加過程

式中：Φ——退化量；

βil——βil＞0，反映第i個應力水平組合下第l個樣品的隨機特征，βili-1～Weibull（m，ηi），m——形狀參數，ηi——分布參數；

tili——i個應力組合水平下的監測時間點；

α——α＞0固定常數；

εilhi（ti，k）——測量誤差，相互獨立且服從標準正態分布εilhi（ti，l）～N（0，σε2）。

2.2 物理模型假設

退化軌跡參數中的隨機效應參數βil服從GΘ（·）分布，分布參數中ηi與應力存在如下關系：

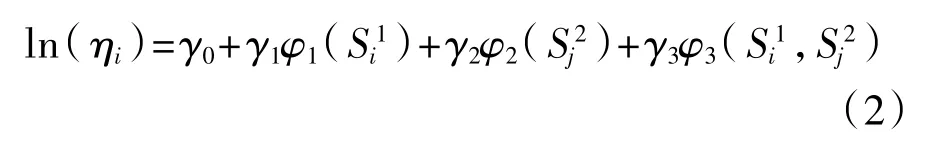
在得到各參數先驗值α、σε2、m、γ0、γ1、γ2、γ3及φ1（Si1）、φ2（Sj2）、φ3（Si1，Sj2）表達式的基礎上可實現雙應力步降加速退化試驗數據的仿真。

3 優化問題描述

3.1 設計變量

（1）應力水平組合數k；（2）加速應力水平組合下的監測頻率；（4）gij為（Si1，監測次數，且gij≥2因而試驗的總時間，其中，tu為單位時間（小時）。從而試驗方案可表示為

3.2 優化目標

選用正常使用應力水平下p階分位壽命漸近方差的局部估計值作為目標函數，即

3.3 約束條件

在樣本量一定的條件下，因費用主要由監測方面的費用組成，故可以用費用函數來代替時間函數對試驗中的設計變量進行約束，具體如下：

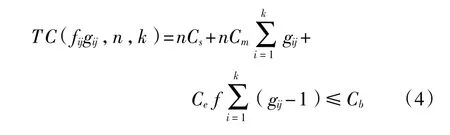
式中：gij≥2，fij＞0，且n和gij均為正整數；

Cm——監測單個樣本監測一次所需的費用；

Cs——單個樣本費用；

Ce——單位時間的操作費用[1]。

4 優化設計方法

4.1 優化算法

小樣本條件下雙應力步降加速退化試驗優化設計具體描述如下：

第1步 構造備選試驗方案集D；

第2步 在備選方案集D中選取一個試驗為備選方案的個數；

第3步 利用Monte-Carlo方法，模擬某型雷達板級雙應力交叉步降加速退化試驗Q次，得到Q組模擬試驗數據：

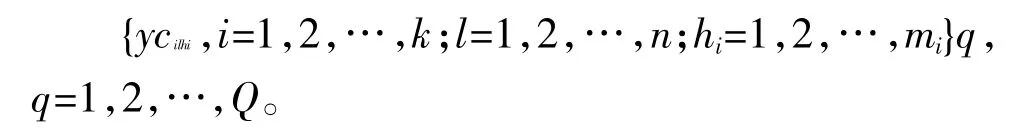
第4步 通過對ycilhi進行統計分析，計算目標函數值fq，r（d）；

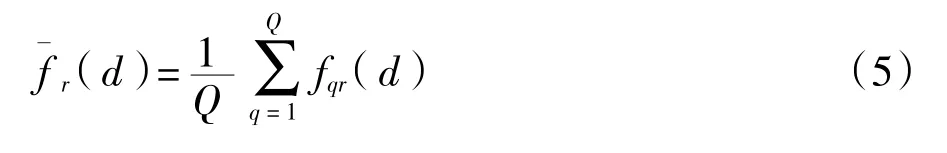
將其作為目標函數值fr；

第6步 返回第2步選取另一個試驗方案重復第2～5步，直至第R個方案完成，目標函數集為

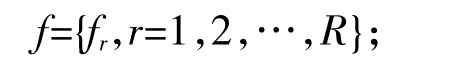
第7步 選取使得目標函數值fr達到最小的方案作為最優試驗方案d*。

4.2 試驗方案的構造

第1步 構造應力水平組合，其中i=1，2，…，k；j=1，2，…，k，為了后續方便討論，令i=j，則的計算公式如下：

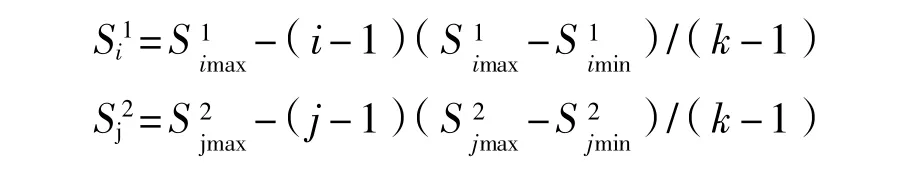
第2步 在給定試驗樣本的條件下，在此總預算費用約束條件下，由文獻[1]可得試驗樣本的上限ku=[（Cb-nCs）/（Ce+2nCm）]，[·]為取整函數；

第3步 令k=2；

第4步 計算給定n下，當監測次數gij=2時，由文獻[1]可得監測頻率f的上限，計算公式為ku=[（CbnCs-2knCm）/（kCe）]，[·]為取整函數；

第5步 令f=1；

第6步 利用下式尋找所有的gij，即

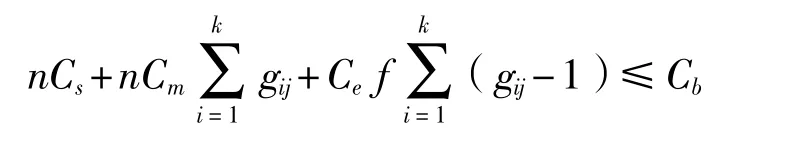
第7步 令f=f+1，返回第6步繼續計算，直到f=fu；

第8步 令k=k+1，返回第4～7步繼續計算，直到k=ku，即可計算出所有應力組合水平下的試驗方案。

4.3 目標函數的計算

目標函數的計算主要涉及p階分位壽命ξp的推導、數學模型及物理模型中先驗參數的估計及Var（ξp0）的計算，這里重點給出AVar（ξp）的計算方法。

首先給出對數似然函數如下：

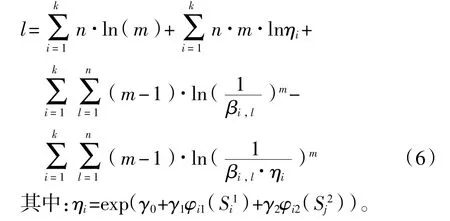
然后通過對式（6）求二階偏導可得到局部Fisher矩陣：

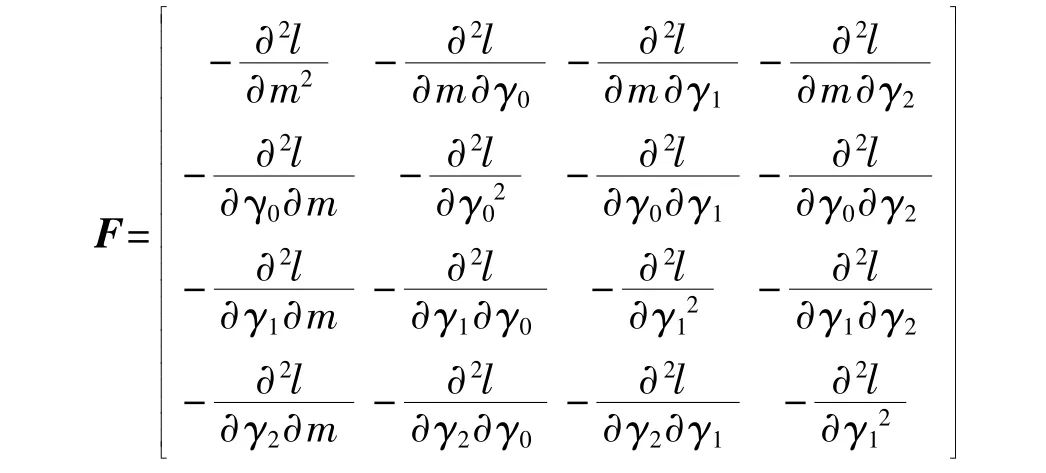
其中，l為對數似然函數，矩陣各項為l的二階偏導數在的值。

根據文獻[4]可很容易推導出p階分位壽命的極大似然估計為

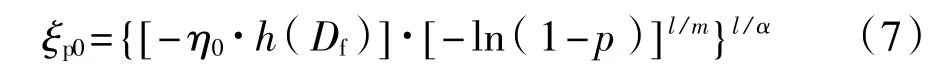
則p階分位壽命ξp0的漸近方差估計為

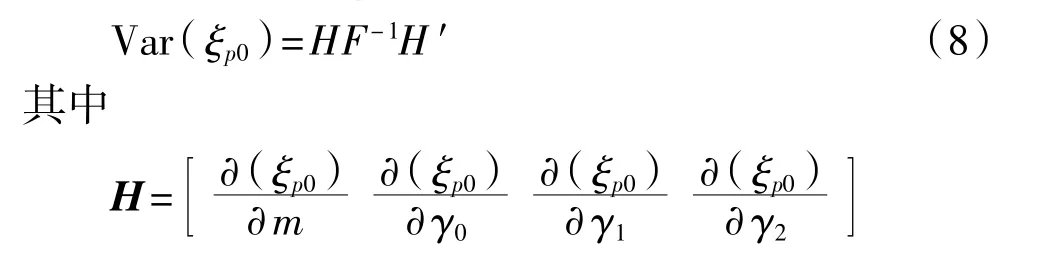
5 實例分析

項目組對該型雷達板級進行雙應力步降加速退化試驗的摸底試驗，通過對功能電路輸出正弦信號的幅度、頻率、相位、直流分量4個特征量進行分析，只有直流分量在加速應力條件下有明顯變化，故可

得該功能電路板的正常使用溫度為298K，相對濕度為25%；最低溫度加速應力為338K，最高為388 K；最低濕度加速應力為30%，最高為85%，失效閾值Df=9。費用參數分別為：總的費用Cr為給定的已知常數Cs=50元，Cm=1元，Ce=1.5元/h，單位監測時間12h。根據瑞藍加速模型

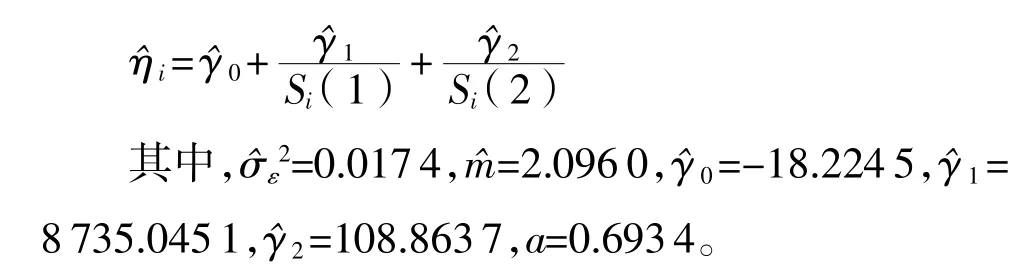
為簡化優化問題，特對試驗變量做以下假設：

（1）為了簡化計算方便分析在此將應力設置為等間隔，即

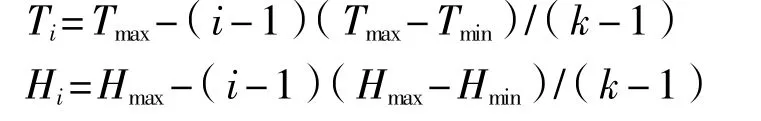
（2）樣本大小n=5，n=8時，按照本文提出的方法對雙應力交叉步降加速退化試驗優化設計進行分析。具體情況如下表1、表2所示。

比較分析表1與表2可以得到如下結論：

（1）在試驗費用（試驗截尾時間）及樣本量大小一定的條件下，目標函數的值隨著應力水平數的增加呈現減小的趨勢。

（2）樣本量大小及應力水平數一定的條件下，目標函數的值隨著試驗費用（試驗截尾時間）的增加呈現減小的趨勢。

在實際試驗時，還需考慮應力水平大小對優化試驗方案的影響，表3給出了n=8，k=3，Cr=2000時最高應力水平變化時的優化試驗方案。

從表3中可以得出當最低應力水平Tmin、Tmax一定時，目標函數值AVar（ξp0）隨著最高應力水平Tmax、Vmax的減小呈現先減小后增大得趨勢。

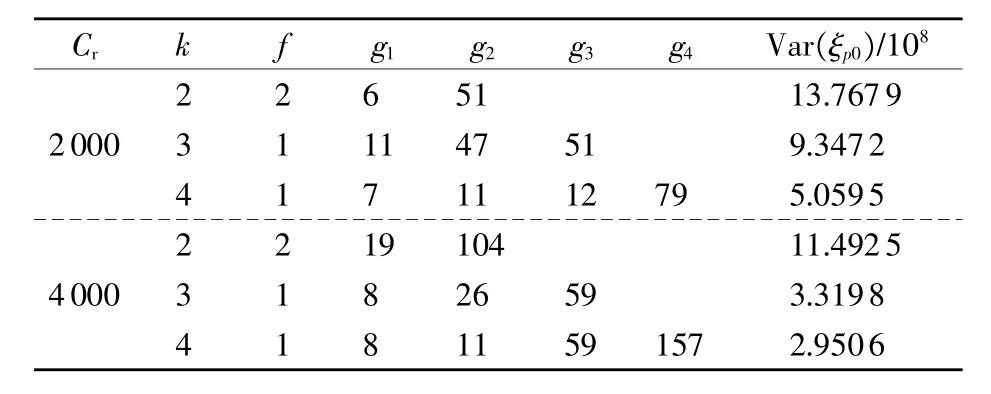
表1 雷達板級雙應力交叉步降加速退化試驗優化設計結果（n=5）

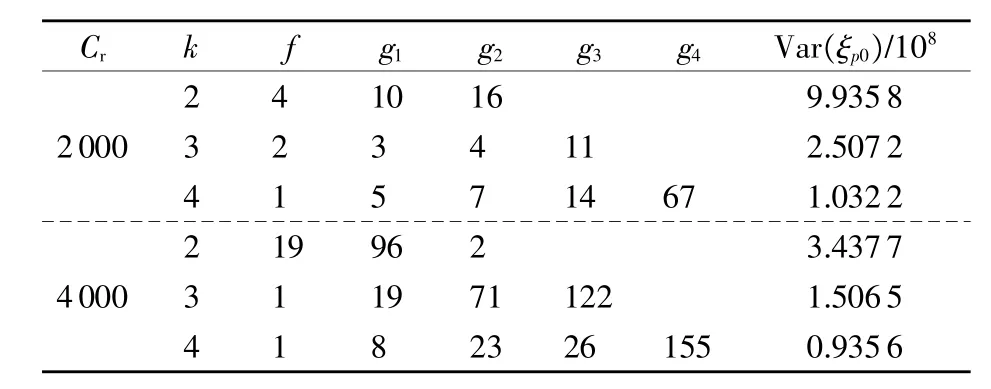
表2 雷達板級雙應力交叉步降加速退化試驗優化設計結果（n=8）

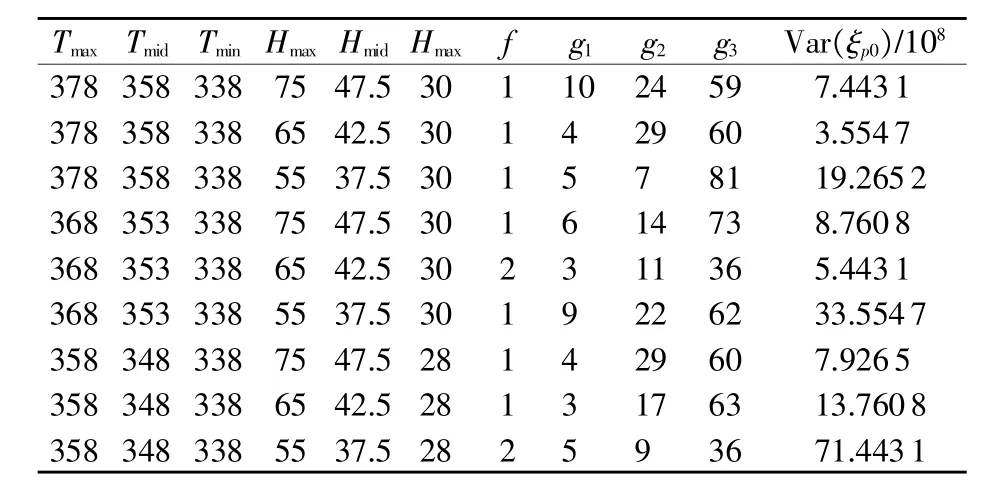
表3 雷達板級雙應力交叉步降加速退化試驗優化設計結果1）

6 結束語

本文對小樣本條件下某型雷達功能電路雙應力交叉步降加速退化試驗優化設計進行了討論，給出了在小樣本量條件下雙應力步降加速退化優化設計的一般方法，分析了不同小樣本量條件下，在不同費用約束下的最優試驗方案；同時以n=8，k=3為例分析了一定費用條件下應力變化對最優試驗方案的影響，得出了一些指導小樣本下雙應力步降加速退化試驗的有用結論，為小樣本量條件下雷達功能電路雙應力步降加速退化試驗優化設計的工程應用奠定了良好的理論基礎。

[1]Wu S J，Chang C T.Optimal design of degradation tests in presence of cost constraint[J].Reliablity Engineering and System Safety，2002，76（2）：109-115.

[2]Zhang J R，Jiang T M，Li X Y，et al.Optimization of step stress accelerated degradation test plans[C]∥17thInternational Conference on Industrial Engineering and Engineering Management，IE and EM 2010.China，2010（10）：947-951.

[3]Liao C M，Tseng S T.Optimal design for step-stress accelerated degradation tests[J].IEEE Transactions on Reliability，2006，55（1）：59-66.

[4]Tang L C，Yang G Y，Xie M.Planning of step-stress accelerated degradation test[C]∥RAMS，Los Angeles，USA，2004：278-292.

[5]Ge Z Z，Li X Y，Zhang J R.Planning of step-stress accelerated degradation test with stress optimization[C]∥Advanced Materials Research，Germany，2010：118-120，404-408.

[6]Li X Y，Jiang T M.Optimal design for step-stress accelerated degradation with competing failure modes[C]∥Annual Reliability and Maintainability Symposium，2009：64-68.

[7]潘正強，周經倫，彭寶華.基于Wiener過程的多應力加速退化試驗設計[J].系統工程理論與實踐，2009，8（29）：64-71.

Optimization design of radar board laver double-cross-step-down-stress accelerated degradation test

PAN Gang，LIANG Yu-ying，Lü Meng，ZHANG Guo-long，LI Wei，MENG Jun
（Ordnance Engineering College，Shijiazhuang 050003，China）

According to the fact that the performance of the radar board laver is affected by several stresses and it is hard to get the performance degraded information in the limited test time of the accelerated degradation test，this paper presented a method of optimal design for the double-step-down-stress accelerating degradation test（DSDS-ADT）on condition of small sample. The procedure of the test was simulated with Monte-Carlo in the condition that the sample size was specified.Number of stress and inspection frequency were considered as variables and the asymptotic variance estimation of 100pth percentile of the lifetime distribution of the product at use condition was considered as the goal function under the constraint of the total experiments cost.The optimal designed model of the radar board laver double-step-down-stress accelerated degradation test（DSDS-ADT）was established.Simulation results verify the feasibility and validity of this method.

radar；performance degradation；DSDS-ADT；optimal design

TB114.3；TN958；TP13；TM930.12

：A

：1674-5124（2014）01-0137-04

10.11857/j.issn.1674-5124.2014.01.034

2012-09-14；

：2012-11-16

國家自然科學基金項目（61271153）

潘 剛（1987-），男，山東新泰市人，碩士研究生，專業方向為武器系統性能檢測與故障診斷。