多類型異構無線網絡連通性研究*

郭敬元，楊 濤，馮 輝，胡 波

（復旦大學電子工程系 上海200433）

1 引言

隨著網絡中越來越靈活的接入需求的發展，不同類型的用戶終端之間的交互變得越來越頻繁，網絡也越來越多地體現出異構和動態的特性。異構性體現在網絡中用戶節點類型和分布的不同；動態性體現在自組織網絡可以靠節點之間的通信組織相連網絡，而不需要中心節點進行協調。典型的例子是認知無線電技術，主用戶和次用戶之間通過機會頻譜共享進行交互。近年來，連續滲流理論[1]的發展和在全局網絡行為方面的應用得到了重視。對于同構的自組織網絡的連通性已有很多研究[2～6]，但對于異構網絡，只有零星的文獻有所研究，其中Ren W等人[7]定義了連通區域的概念，并推導出以節點密度、干擾范圍和傳輸范圍形式給出的連通性充分和必要條件，首創了將機會頻譜的占有和釋放與布爾滲流模型中的連通分量和空分量進行耦合求解。而對于次用戶之間的合作對連通性的影響，Chon W[8]將異構網絡建模為多個自組織網絡，得到噪聲受限和干擾受限普通衰落信道條件下的平均度和度分布，并以此為基礎分析了合作滲流。參考文獻[9]引入了認知無線電圖模型，并考慮可用信道的個數和活動的主用戶，由此得出在滿足次用戶網絡滲流前提下的主用戶臨界密度。Wang P等[10]考慮到動態連接對連通性的影響，證明如果次用戶密度大于一個臨界值，則網絡在任意時刻都可以保持連通，即使網絡一直經歷動態變化；還證明即使在任意時刻整個次用戶網絡是不連通的，也有可能存在一條時延通路使得某個次用戶以概率1發送信息到目的地，而這一時延與發送端到接收端的歐式距離呈漸進線性關系。

網絡連通性的研究，分為有限范圍和無限范圍，本文研究后者。從滲流角度研究無線多跳網絡的連通性，主要特點是連通性取決于某個參數，滲流模型的分量可能有兩種情況：所有連通分量全部有限；存在一條無限長的連通分量。后者被定義為無限網絡的連通。

網絡連通性研究的目標就是要找到使得網絡能夠連通的條件，參見如下連通性的定義：如果網絡中存在一條無限長的連通分量，則稱網絡是連通的。所謂無限長的連通分量，指圖中無限長的由節點連接而成的一個分簇，只要存在無限長連通分量的概率不為0，就認為網絡是連通的。

網絡滲流的概念是從物理學領域發展出來的，指的是從無連通分量到出現連通分量的相變過程，即物質在外部參數（如溫度、壓力等）的連續變化之下，從一種相忽然變成另一種相，最常見的是冰變成水。將網絡滲流應用到信息科學領域，通過隨機幾何圖實現。隨機幾何圖描述了點和邊的關系，點和邊的分布以及邊和邊的連接方式決定了一個隨機幾何圖的性質，點的分布服從某個特定的點過程。點過程是從概率空間到某空間E上的點度量空間的映射Φ，點度量是局部有限的，且只取整數值，表示如下：

其中，δXi是狄拉克測度，Xi是隨機變量，在E上取值，是d維歐幾里德空間,d≥1。連續滲流領域普遍采用的模型是泊松點過程分布的點，當且僅當它們之間的距離不超過r時，這兩點相連，記為G（X，r）。雖然泊松分布過程被廣泛用作分析隨機網絡連通性，但并不總是符合實際情況，簇分布被證明更加接近城市熱點地區的實際情況[11,12]，不過此類分布的連通性仍然未知。常規的異構網絡分析主要側重于兩類異構用戶，即主用戶和次用戶之間的交互行為，但實際上次用戶也是由多種類型的終端構成的，如具有不同傳輸范圍的終端。本文通過對單類型節點和多類型用戶節點組成的異構網絡的分析，推導網絡的連通性與各參數之間的影響。

2 網絡模型與應用

目前主要從兩個角度進行網絡連通性研究，分別是泊松布爾模型和隨機連接模型。布爾模型中，點的分布隨機，每個點的覆蓋范圍隨機（連續滲流中采用固定大小圓盤模型），任意節點可以和自己覆蓋范圍內的所有節點連接；隨機連接模型中，點的分布隨機，但每個點并不是跟自己圓形覆蓋范圍內的節點連接，而是由一個隨機連接函數決定與某一個節點進行連接。

從布爾模型和隨機連接模型兩個角度分別分析異構網絡的連通性，其中布爾模型又分為單類型節點異構網絡和多類型節點異構網絡。對于每種模型，都有一個對應的實際應用網絡進行舉例分析，如移動自組織（Ad Hoc）網絡、認知無線電。

2.1 布爾模型

2.1.1 單類型節點異構網絡

Ad Hoc網絡的連通性受到廣泛關注。Ad Hoc網絡是一種多跳的臨時性自治系統，原型是美國早在1968年建立的ALOHA網絡。作為一種分布式網絡，Ad Hoc網絡是一種自治、多跳網絡，整個網絡沒有固定的基礎設施，能夠在不能利用或者不便利用現有網絡基礎設施（如基站、AP）的情況下，提供終端之間的相互通信。由于終端的發射功率和無線覆蓋范圍有限，距離較遠的兩個終端如果要進行通信就必須借助于其他節點進行分組轉發，這樣節點之間構成了一種無線多跳網絡。

簡單地用泊松分布分析Ad Hoc網絡過為理想化，因為假定所有用戶節點平均分布在有限區域中不太符合實際情況。實際的用戶節點分布經常是在某些熱點地區稠密，在其他非熱點地區稀疏，從而可引出簇分布，即用戶節點有向各個中心節點靠攏的趨向。分析單類型用戶時，用簇分布中的一種——Thomas分布模擬真實用戶節點分布。

當次用戶只有一種類型（即所有次用戶傳輸范圍相同）且分簇分散在各處時，研究臨界點與其他簇分布參數的關系。采用Thomas點過程作為簇分布的模型，圖1(a)為一個Thomas過程在單位方格中的示例。在Thomas過程中，節點分為兩類：一類是簇頭節點，即中心節點，如圖1(a)中的“”點，服從泊松分布，均勻密度為λ；另一類是圍繞在各個中心節點周圍的普通節點，如圖1(a)中的黑色圓點，服從高斯分布，均值為μ，協方差矩陣為σ=diag(σx,σy)，圖1(a)中的圓圈是以中心節點為圓心、某個固定的σ=σx=σy為半徑所做的圓。所有普通節點都可作為發送端和接收端，傳輸范圍均為r。

直觀來說，當節點分布從泊松分布擴展到Thomas分布時，滲流產生將變得更加困難。原因在于隨著進一步的聚簇，越來越多的內部節點的連接效應會遞減，直到逐步發展到全局連通性主要由每個簇的邊緣節點決定。一旦這些邊緣節點可以連接相鄰的簇的邊緣節點，這兩個簇就可以連通。從這種思路出發，引用平均場估計 （mean field approximation）理論推導傳輸半徑的臨界值。平均場估計理論被用來分析多體物理系統中的交互行為，用均值代替所有交互，將多體問題有效地簡化為單體問題。建模時將所有周邊信息視為一個統一的變量，并將所有的殘余節點視為確定性的平均場，本質即統計均值。

對于Thomas過程而言，可以把簇的內部和外部的節點等效為一個半徑確定但未知的圓，使得這些節點等效于這個圓上某些均勻分布的點（如圖1(b)所示）。根據參考文獻[13]，可以先得到圓內點的距離分布以及圓上點的平均距離（即圓上點的個數）。假設兩個簇的等效圓上各有3個均勻分布的節點，為了研究這兩個簇之間的隨機連通性，假定左邊的簇O1固定，讓右邊的簇O2以簇頭為中心，沿某方向轉動。當總存在至少一個節點在弧de上時，則總存在一個節點c可以連接到O2的邊緣節點，以使兩個簇連通，途經節點{a，b，c，d，e}。

2.1.2 多類型節點異構網絡

單一類型的簇分布的用戶節點并不能反映其他一些重要的實際場景，應當引入混合類型的用戶節點。例如在認知無線電中，有主用戶和次用戶兩類，而次用戶本身也可能有多種類型。考慮到理論分析的可行性，構建以下泊松分布的認知無線電模型。

無限的二維歐式空間中，泊松分布的次用戶網絡疊加在泊松分布的主用戶網絡上。這與同構網絡有著顯著的區別，即多類次用戶節點之間通信鏈路的存在與否不僅取決于它們之間的距離，還跟周圍主用戶的特征（荷載、拓撲、干擾容限）和收發行為有關。

假設主用戶發射端以密度為λp的二維泊松點過程分布，對每個主用戶發射端來說，它的接收端均勻分布在傳輸距離為Rp的范圍內。假定所有主用戶發射端的發射功率相同，信號經過相同的路徑損耗，則主用戶接收端也以密度為λp的二維泊松點過程分布且與發射端點過程相關，主用戶對周圍次用戶的干擾范圍是RI。

次用戶疊加在主用戶之上，也服從泊松分布，分為兩類（T1與T2），具有混合密度λs，即T1次用戶密度為pλs，T2次用戶密度為（1-p）λs，傳輸范圍分別是rp1、rp2，干擾范圍分別是rI1、rI2。以參考文獻[7]中的模型為參考，并拓展到兩類次用戶的情況，構建次用戶之間的雙向連接，如圖2所示。

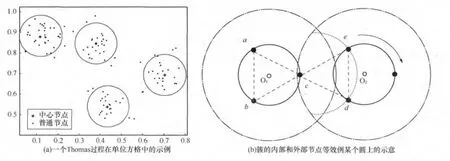
圖1 Thomas過程

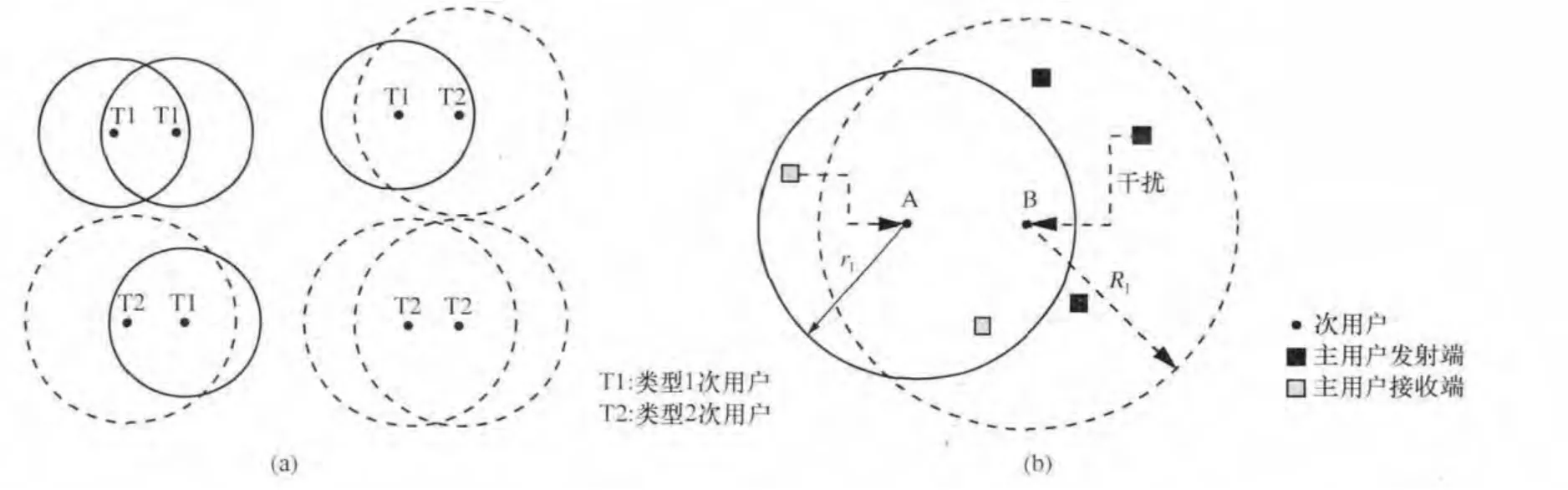
圖2主用戶與次用戶示意

圖2 (a)中，次用戶A到次用戶B的通信鏈路可分為4種情況：T1→T1、T1→T2、T2→T1、T2→T2。圖2(b)為T1→T2放大后的詳細情況。為了解決網絡連通性的問題，構建隨機場多類型分支（MBPR）過程，從理論上推導分布參數對網絡連通性的影響。可以想象，從某個用戶節點S1開始，把與之相連的用戶節點組成的連通分量“提起來”變成一棵以S1為根的樹（如圖3所示），這樣無限長連通分量的存在性就等價于這棵樹（分支過程）能否無限生長下去。問題的本質就是，隨機場如何決定樹的每一代的復制分布。如前所述，用戶的不同類型指的是不同的傳輸半徑，從而MBPR可以被歸結為具有不同傳輸半徑的用戶能否通過合作使得這棵樹無限延伸，由此引出兩類次用戶連通的必要條件。當有更多類型的次用戶時，可以方便地從兩類次用戶進行拓展。

圖3 多類型分支過程

定理 以上定義的混合次用戶網絡能夠發生滲流的必要條件是：

證明 基本思路是構建一個MBPR，每個節點都分別對應一個類型t∈T={1，2}，每個節點都可以“生出”任意類型的子節點，即任意次用戶都可以和滿足以下條件的T1和T2次用戶進行通信。

·條件1：它們之間的距離至多為max{rp1，rp2}；

·條件2：它們之間存在雙向機會頻譜，即次用戶A的rI1或rI2范圍內無主用戶接收端，RI范圍內無主用戶發射端，見圖2(b)。

對于每個節點來說，如果它屬于類型t，則有一個與它關聯的隨機向量ζt={ζt1，ζt2}，其中ζtj是一個隨機變量，表示由第t類節點產生第j類節點的個數。把它的期望記為mij，則一階矩量矩陣可由A構建。根據參考文獻[16]的定理，MBPR在ρ=1、ρ<1、ρ>1時分別為臨界、次臨界和超臨界狀態，其中ρ是矩陣A的譜半徑，即A的最大正特征值。

在上述分支過程中，矩陣A的4個元素可以用與參考文獻[7]類似的方法求得，式(4)給出m12元素的求解，其他3個元素可采用類似方法求得。

圖4 SI2（r，θ，Rp，t，rI1，rI2）為陰影部分

2.2 隨機連接模型

用圓盤模型進行理論分析較為方便，但在實際應用場景中，由于功率限制與通信干擾及能量消耗等因素，用戶節點并不可能跟通信范圍內的所有節點都建立連接，而只能跟通信范圍內的某些節點建立連接。此場景可抽象為由隨機連接函數決定節點間連接的隨機連接模型。先介紹不考慮用戶節點間距離的Erd仵s-Rényi（ER）模型，再擴展增加距離約束。

在圖模型中，ER模型指在每一對節點中，都以相同的概率p存在一條邊。近年來，Achilioptas過程因為能夠提前或推遲滲流相變的發生而受到很多關注。在2000年的一個會議中，Achlioptas D提出，從一個沒有邊的圖出發，每一步從所有可能的邊中找到兩條獨立的邊e1和e2，再根據“乘積規則”[15]選擇兩條邊的一條進行連接。而“乘積規則”，就是通過選擇邊的兩點所在分量的度的乘積大的一條，選擇對應的邊。問題在于：乘積規則會對產生的邊的大小有何變化？對圖的滲流有什么影響？這里給出一個仿真來展示ER模型和乘積規則對于Thomas過程臨界行為的影響。

如圖5(a)所示，橫坐標為次數，即每次根據乘積規則添加一條邊，縱坐標為最大連通分量的大小。可以看到，乘積規則會一開始推遲相變的發生，最大連通分量一直保持較小的增長，直到到達臨界點，最大連通分量迅速增大到90%以上，產生爆炸效應，從ER模型的一階相變變為二階相變，這種選擇方法產生所謂的“爆炸滲流”現象。

更進一步考慮爆炸滲流，一種方法是增加距離約束，即讓兩個用戶節點之間的連通概率與距離有關。一般連通性會隨著距離的增大而減少，而是否連通取決于兩個節點在實際網絡中的真實距離，這樣乘積規則就可以修改為增加距離參數，即選擇以下值：

這被稱為“最小引力規則”，用來衡量距離對最大連通分量出現的影響。其中，d是一個可調參數，衡量距離對乘積規則的影響，M1與M2表示第一條邊的兩個節點所對應的連接分量的大小，R12表示這兩個點的距離，M3與M4表示第二條邊的兩個節點所對應的連接分量的大小，R34表示這兩個點的距離。引入距離對爆炸滲流的影響如圖5(b)所示，其中粗線表示ER模型，其他7條曲線分別是d從1～7時的乘積規則模型，隨著d的增大，爆炸特性逐漸減少。可以推測存在某種標度，當d趨于無窮大時，爆炸滲流趨于ER模型。

3 仿真試驗與分析

使用蒙特卡洛仿真驗證第2.1節中二維Thomas過程的臨界連接現象，目的是研究何時以及在哪里會發生滲流、不同參數之間的交互如何影響相變的發生。通過有限尺度的標定，首先設置初始值，在單位方格內以Thomas分布確定點的位置。保持3個參數不變而改變另一個參數，得到如圖5所示的觀察結果，其中，縱坐標是最大連通分量所占總節點個數的比例，橫坐標是對應的改變參數。

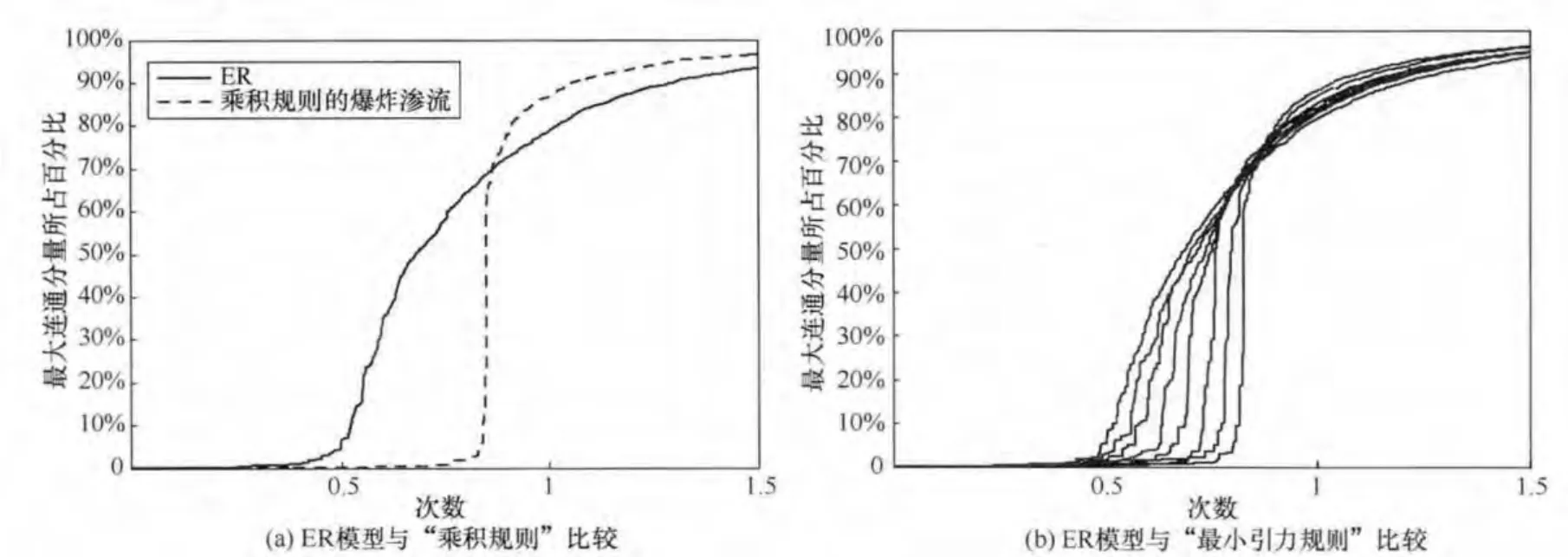
圖5 兩種爆炸滲流模型相變比較

圖6(a)是通信范圍r對連通性的影響。顯然，如果不要求全連通，則可以顯著地減小r。聚簇參數σ對最大連通分量的影響較微小，因為較小的σ會加速最大連通分量的出現。圖6(b)是μ對連通性的影響，可以看出，增大μ對于增強網絡連通性的效率不高，原因是這只是增大了簇頭節點周圍的平均節點數目，如果沒有增大λ，連通性很難通過只擴大每個簇的節點數而提高。圖6(c)是λ對連通性的影響，因為增大λ不僅會增加簇頭點數，而且還有附帶的周圍節點，密度參數λ對整個網絡連通性的影響最大。圖6(d）是σ對連通性的影響，這個參數的影響比其他幾個參數更復雜些，隨著σ的增大，最大連通分量的大小先增后減。

尋找臨界值rc、λc較為困難，可以從工程應用角度擬合得到rc的近似值。擬合的一種方法是對圖6(b)曲線中的μ進行微分，尋找最大的斜率點r作為臨界值rc并與每個μ對應，從而得到二階對數多項式擬合。

4 結束語

從滲流角度研究了自組織異構通信網絡的連通性問題，分別從布爾模型和隨機模型的角度出發，對單類型用戶網絡和多類型用戶網絡在不同場景下進行建模，從理論推導和仿真的角度分析了認知無線電系統中次用戶網絡的連通性。上述研究對多類型異構網絡的部署與設計具有一定的指導意義。

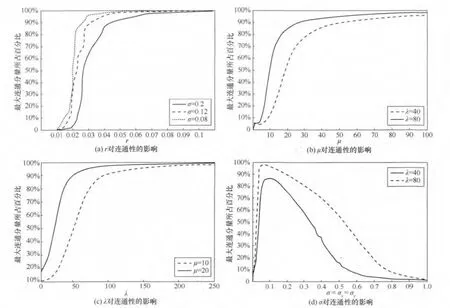
圖6 各參數對最大連通分量的影響

1 Meester R,Roy R.Continuum percolation.Cambridge University,1996

2 Cheng Y C,Robertazzi T G.Critical connectivity phenomena in multi-hop radio models.IEEE Transactions on Communications,1989,37(7)

3 Dousse O,Baccelli F,Thiran P.Impact of interferences on connectivity of Ad Hoc networks.ACM/IEEE Transactions on Networking,2009,13(2):425～436

4 Dousse O,Franceschetti M,Macris N,et al.Percolation in the signal to interference ratio graph.Journals on Appl Prob,2006(43):552～562

5 Kong Z,Yeh E.Connectivity,percolation,and information dissemination in large-scale wireless networks with dynamic links.IEEE Transactions on Information Theory,2009(1)

6 Vaze R.Percolation and connectivity on the signal to interference ratio graph.Proceedings of the IEEE Conference on Computer Communications(INFOCOM 2012),Orlando,Florida,USA,March 2012

7 Ren W,Zhao Q,Swami A.Connectivity of heterogeneous wireless networks.IEEE Transactions on Information Theory,2011,57(7):4315～4332

8 Ao W C,Chen K C.Cognitive radio-enabled network-based cooperation:from a connectivity perspective.IEEE Journal on Selected Areas in Communications,2012,30(10):1969～1982

9 Lu D,Huang X,Li P,et al.Connectivity of large-scale cognitive radio Ad Hoc networks.IEEE INFOCOM,2012(1)

10 Wang P,Akyildiz I F,Al-Dhelaan A M.Percolation theory based connectivity and latency analysis of cognitive radio Ad Hoc networks.Wireless Networks,2011(17):659～669

11 Li D,Gross J.Robust clustering of Ad Hoc cognitive radio networks under opportunistic spectrum access.Proceedings of IEEE International Conference on Communication,Kyoto,Japan,Jun 2011

12 Liu S S,Lazos L,Krunz M.Cluster-based control channel allocation in opportunistic cognitive radio networks.IEEE Transactions on Mobile Computing,2012,11(10):1436～1449

13 Srinivasa S,Hartin M.Distance distributions in finite uniformly random networks:theory and applications.IEEE Transactions on Vehicular Technology,2010,59(2):940～948

14 Erdos P,Renyi A.On the evolution of random graphs.Publ Math Inst Hungary Acad Sci,1960(5):17～61

15 Achlioptas D,Souza R M D,Spencer J.Explosive percolation in random networks.Science,2009(323)

16 Serra M C.A Multi-Type Branching Processes Approach to the Evolutionary Dynamics of Escape,2007