加速退化試驗方案優化問題經驗參數估計方法
沈崢嶸,時鐘,游曼
(工業和信息化部電子第五研究所,廣州 510610;廣東省電子信息產品可靠性技術重點實驗室,廣州 510610;廣州市電子信息產品可靠性與環境工程重點實驗室,廣州 510610)
引言
產品失效是一個十分復雜的過程,一些產品的失效和應力累計有關,當產品性能參數隨著時間產生退化,最終超出產品性能正常閾值,導致產品故障或失效。通過這一原理,我們可以在沒有失效數據的情況下,對產品的壽命進行評價。然而,許多產品的退化速度都很緩慢,在實驗室中我們可以采用加速退化試驗方法。加速退化試驗方法在不改變產品失效機理的前提下,通過加大產品的敏感應力(如熱應力、電應力或機械應力等)加快產品的性能退化,利用高應力水平下的退化數據,外推正常使用應力下產品的壽命和可靠性。加速退化試驗需要開展多組試驗,投放多個試驗樣品,應力值的選取和樣本量的投放以及截尾時間或截尾數的確定直接影響了加速退化試驗的效率和質量,這樣加速退化試驗的最優設計問題成為試驗方案設計的關鍵因素。
1 加速退化試驗模型
為了便于討論,以下說明和推導是基于性能參數退化是朝著性能參數的合格上邊界退化的,即為正漂移布朗運動。
退化方程為:
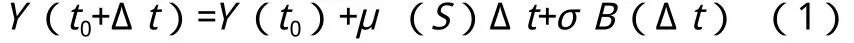
式中:Y(t)——在t時刻時,產品的性能值,在t0(初始)時刻時,產品的性能(初始)值為Y(t0),在t0+Δt時刻,產品的性能值為Y(t0+Δt);
μ——漂移系數,即某應力水平下的退化速度,μ>0;
σ——擴散系數,σ> 0,在整個加速退化試驗中,σ不隨應力而改變;
B(Δt)——標準布朗運動,B(Δt)~N(0,Δt)。
因此得到:
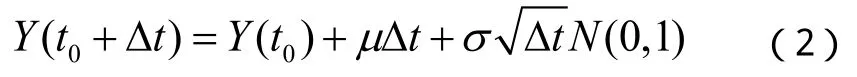
退化率函數是應力的函數,其與應力的關系可以表示為:
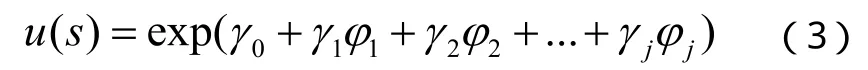
其中iφ為應力元素,可以是溫度、振動、電應力、濕度或電應力等,jγ為其系數。
式(3)的關系可以描述大多數加速模型,如Arrhenius模型、Eyring模型和Peck模型等。
2 試驗方案優化問題
2.1 加速退化試驗方案
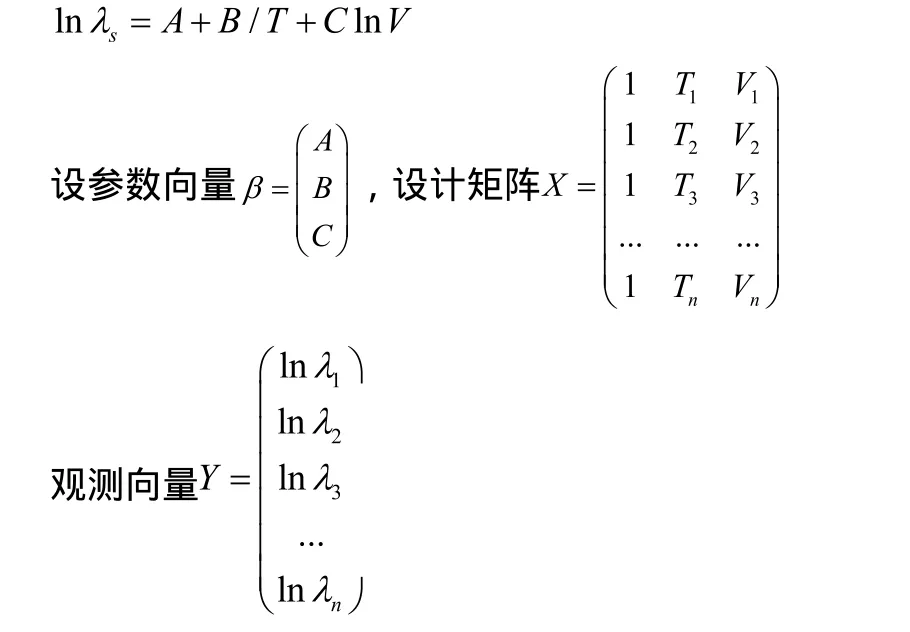
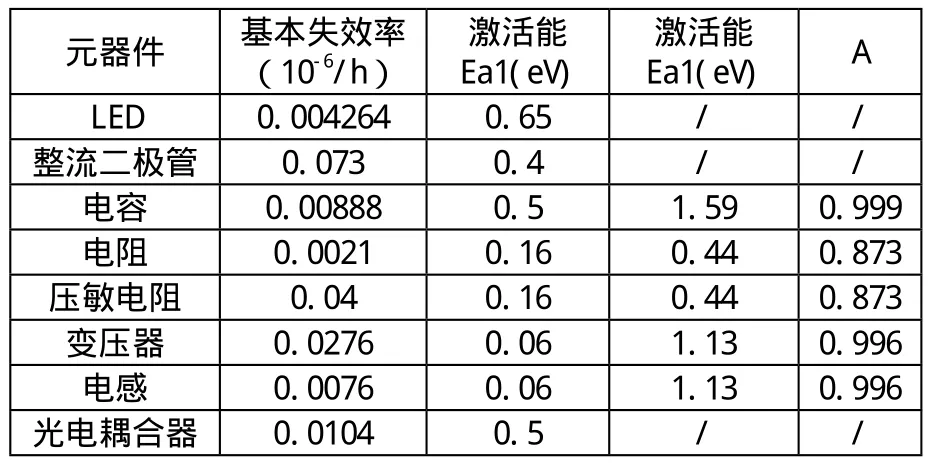
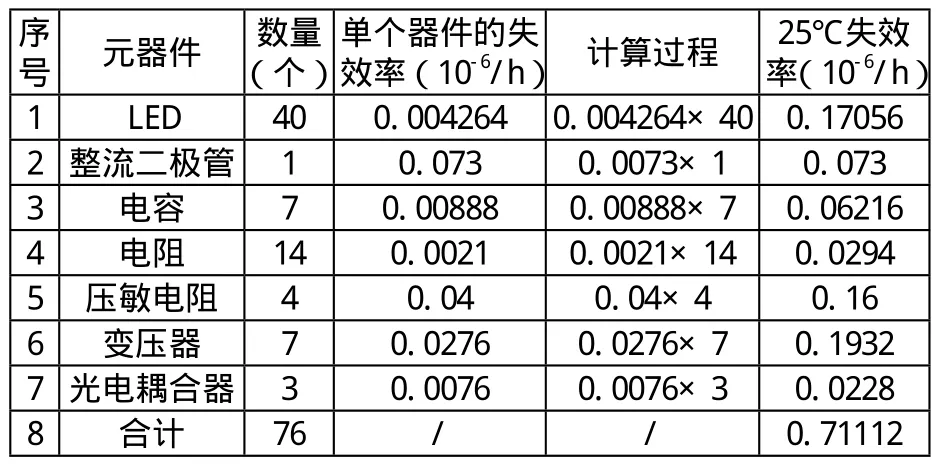
恒定應力加速退化試驗的核心目的是利用試驗數據對式(3)中的未知參數 γi(i = 1,...,p)進行估計,因最小二乘估計要求設計矩陣X為列滿序,即設計矩陣的行數要大于等于其列數,基于這一理論,恒定應力加速退化試驗的試驗組數和未知參數數目應滿足:n≥p。假設在恒定應力加速退化試驗中產品不發生失效,每種應力Sl(l=1,...L)共K個應力水平(Sil,...,SiK),產品在每種應力下的極限工作應力值記為Simax,正常應力記為Si0,則應有(Si0≤Si1 對于單應力加速退化試驗,試驗組數n就是應力的n個水平。對于多應力加速退化試驗,試驗組數n是各應力的 n個組合。 獨立增量的概率密度函數為: 其對數似然函數為: 優化目標為其參數極大似然估計的協方差陣最小: 對于恒定應力加速退化試驗,其模型參數的評估精度可以用參數的極大似然估計的協方差表示,根據Cramer-Rao不等式,只要使得 fisher信息矩陣I()θ的行列式最大,就表示模型參數評估精度最高。 即 maxdet(I(θ)) 約束條件從兩方面考慮,試驗成本和試驗變量范圍的約束。 試驗成本考慮:樣本費用,即樣本單價與樣本量的乘積;實施試驗的費用包括試驗箱、測試設備的耗損折舊,人力、電力等資源的消耗,即試驗單價與試驗時間的乘積。試驗費用約束為 式中,Ct為試驗總成本;Cu為單位時間內實施試驗的費用;Cd為樣本單價。 試驗變量實際取值約束條件為 假設退化模式不隨應力改變,為使各組應力下都有足夠的退化信息,退化率小的應力組合試驗不小于退化率達的組合時間,即 綜上所述,優化問題可以描述為: 以上所述的優化問題十分復雜,求得其解析解十分困難,我們只能用空間搜索的辦法找到其數值最優解。 首先根據目標函數和費用約束確定試驗時間和樣本量的取值空間。 其次,根據試驗情況,給出各應力水平、樣本分配比和時間分配比率的搜索步長,搜索所有滿足約束條件,各組應力的選取應滿足退化率約束,構成應力S的取值空間;同樣選擇合適的步長,搜索滿足約束條件的時間分配比和樣本分配比的取值空間。 由各變量的取值空間,構建整個優化問題解的方案集,計算方案集中每一個方案對應的目標函數。 開展加速退化試驗的目的就是對退化函數中的參數進行估計以推導出正常應力下的退化率,進而確定產品性能參數的首達時間(即壽命)。但如果對退化率中的待定參數一無所知,就無法對加速退化試驗進行優化設計,這是一個矛盾。 在開展加速退化試驗優化設計前,需要對退化率函數中待定參數進行粗略估計,產品設計人員可以按照經驗給定待定參數。在沒有更多先驗信息的情況下,本節提供基于失效率轉化的方法對退化函數中的參數進行粗略估計。 利用電子元器件失效率轉化方法獲得退化函數待定參數的粗略估計步驟如下: 3.1 獲得完整受試產品的元器件清單。 3.2 查閱GJB 299C得到所有元器件的基本失效率。 基本失效率選取器件在常溫、基準電應力環境溫度下的失效率。 3.3 利用IEC 61709提供的方法,計算多組應力下的元器件失效率。 其失效率可以表示為: λref——基準條件下的失效率; πU——電壓應力系數; πI——電流應力系數; πT——溫度應力系數。 式中: ——工作電壓(V); Uref——基準電壓(V); Urat——額定電壓(V); C2,C3——常數。 上述公式給出了失效率與電壓關系的經驗模型。 溫度應力系數Tπ 式(9)是基于Arrhenius方程的經驗模型,它描述了溫度與失效率的關系。理想情況下,應針對每類失效模式進行計算,但通常應用時是采用所有失效模式的平均激活能來計算溫度對失效率的影響。必須說明的是,由于溫度與不同潛在失效模式的激活能有關,在后面這種情況中激活能也可能是關于溫度的函數,但是這種受溫度的影響通常可忽略。 某些情況中可采用式(8)這種包含兩個激活能的更為復雜的模型描述溫度和失效率的關系,含兩個激活能(Ea1,Ea2)的模型的使用被認為可充分為失效率和溫度關系建模。(有時將其稱為競爭風險,詳見JESD-85) 為避免基準溫度變化時激活能隨溫度變化,阿倫尼斯方程已作標準化處理: 在式(8)和式(9): A——常數; Ea1,Ea2——激活能(eV); k0=8.616×10-5eV/K; T0=313K; Tref=θref+273(K); Top=θop+273(K)。 此處θref和θop(℃)表示的是: ——對于集成電路:θref為基準的實際(等效)結溫,θop為實際的(等效)結溫; ——對于分立器件和光電器件:θref為基準結溫,θop為實際結溫; ——對于電容器:θref為基準的電容器溫度,θop為實際的電容器溫度; ——對于電阻器:θref為平均基準溫度,θop為平均的實際溫度; ——對于電感器:θref為線圈的平均基準溫度,θop為線圈的平均實際溫度; ——對于其他電子元器件:θref為基準環境溫度,θop為實際環境溫度。 3.4 計算各應力下受試產品總失效率 根據基本可靠性的串聯模型,各個單元的失效率等于包含的所有元器件失效率之和,產品的失效率等于各個單元的失效率之和: 以退化率函數 d( S )= exp(A + B/ T + C lnV)為例,大致估算參數A、B、C的取值,該式中,T為絕對溫度,單位為K;V為電壓,單位為V。 對退化率函數兩邊取對數,有lnd(S)=A+B/ T+ClnV,認為退化率和失效率是正向相關的量,問題轉化為: 每個元器件在應力條件下的失效率為相應的應力系數和基準失效率的乘積,基準失效率可以通過相關數據手冊查到(GJB 299或Siemense標準)。 3.5 利用最小二乘法計算退化率函數中的待估參數 設X是列滿秩矩陣,參數向量的最小二乘估計為: 此處涉及到高維矩陣求逆,可利用Matlab等數值計算軟件求得。 某型LED照明燈具元器件的基本失效率和激活能見表1,其元器件基本失效率參看GJB 299C,激活能和參數A查看IEC 61709。 25℃下,該LED照明燈具的是效率計算過程見表2。 85℃下該型產品的失效率計算過程見表3。 表1 某LED產品主要元器件失效率 表2 該型產品25℃的是效率計算 表3 該型產品85℃下失效率預計值 把溫度和對應的是效率帶入(6)式中,可得到參數A、B的粗略估計。 可得B=-5640,A=18.6 這樣可以粗略的認為產品退化方程滿足u(T) = exp(18.6-5640/T),進而開展優化設計。 以上總結了基于布朗漂移運動的加速退化試驗方案優化設計數學表達,給出了一種基于可靠性預計的加速退化試驗方案優化問題經驗參數粗略估計方法,為工程解上決這一問題提供了參考。 [1]茆詩松,高等數理統計(第二版)[M].北京:高等教育出版社, 2006. [2]趙建印,基于性能退化數據的可靠性建模與應用研究[D].湖南:國防科技大學,2005. [3]葛蒸蒸,姜國敏 等. 基于D優化的多應力加速退化試驗設計[J]. 系統工程與電子設計. 2012, 4. [4]Edward P.C Kao An introduction to stochastic processes[M], Wadsworth Publishing Company,1997. [5]IEC 61709, Electric components Reliability Reference conditions for failure rates and stress models for conversion [S]. [6]JESD-85, Methods for Calculating Failure rates in units of FITs[S].
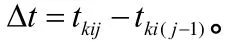
2.2 優化目標
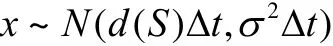
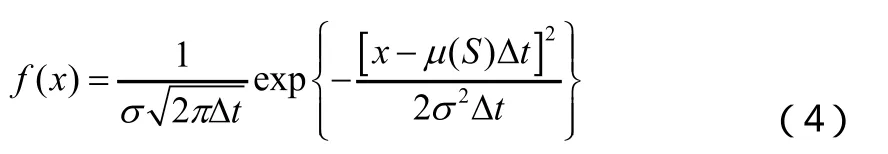
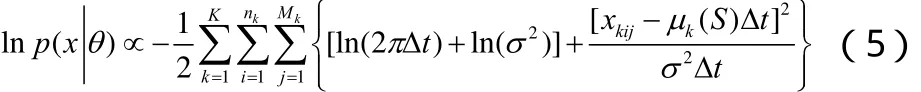
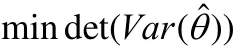

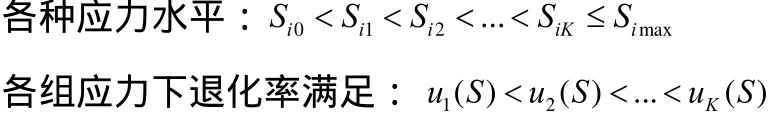
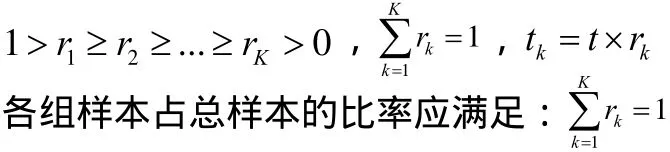
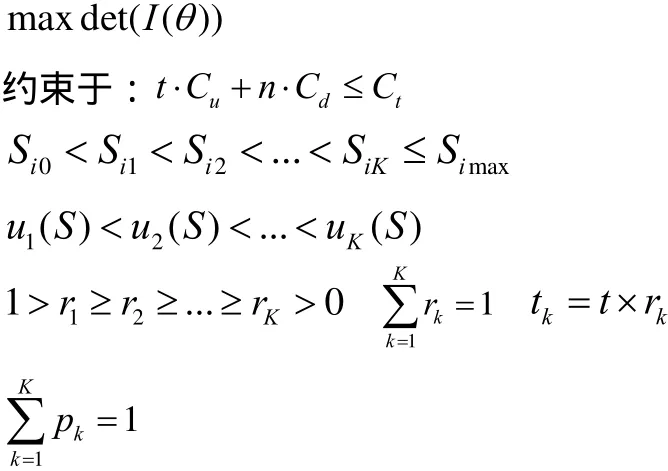
3 經驗參數的粗略估計
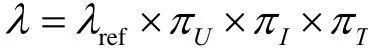
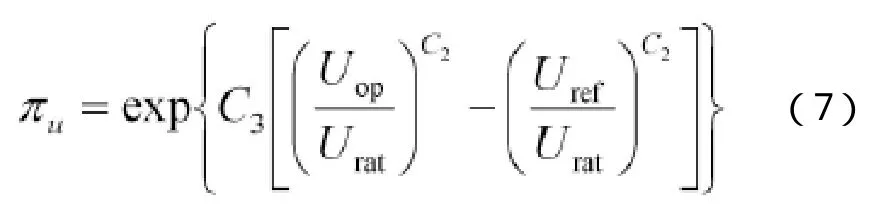
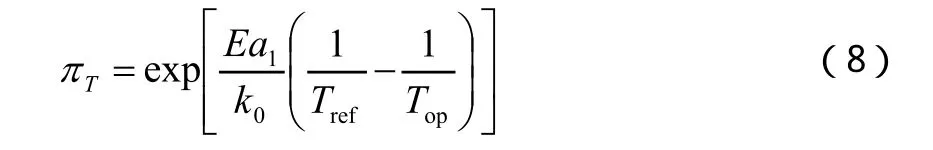

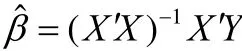
4 算例

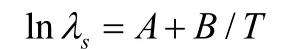
5 結束語

