淺水航道艦船水壓場理論解及其計算

孫幫碧，張志宏，劉巨斌，鄧 輝

(海軍工程大學理學院，湖北武漢 430033）

淺水航道艦船水壓場理論解及其計算

孫幫碧，張志宏，劉巨斌，鄧 輝

(海軍工程大學理學院，湖北武漢 430033）

基于淺水波動勢流理論，建立亞臨界航速和線性跨臨界航速淺水波動控制方程。基于薄船假定，利用傅里葉積分變換法獲得淺水航道艦船水壓場理論解。通過數值求解，分析艦船航速、水深、航道寬度、色散效應對艦船水壓場特性的影響，并與源匯分布法計算結果進行對比，驗證所建立的淺水航道艦船水壓場數學模型和計算方法的正確性與有效性。

淺水;航道;艦船;水壓場;理論解

0 引言

航行艦船引起的水底壓力變化簡稱為艦船水壓場。艦船水壓場是艦船物理場的自身特性，是設計新型水雷及研制水壓掃雷具以及艦艇自身防護的依據。Tuck［1］基于漸近匹配展開法，得到淺水薄船水壓場的近似解;Muller［2］利用有限水深興波源勢方法，在船舶縱向剖面上布置源匯，給出薄船、線性自由表面條件下的艦船水壓場計算公式;Sahin和Hyman，Nguyen［3－4］等采用有限水深格林函數方法，系統開展了潛艇、水面艦艇和氣墊船水壓場的理論建模和數值計算工作;Jiang［5］和 Gourlay［6－7］基于淺水波動勢流理論對艦船興波和升沉與縱傾作了分析與計算;黎昆［8］、繆濤［9］等利用面元法計算艦船在水底引起的壓力分布。

1 控制方程

假設流體為理想不可壓流體作無旋運動，艦船沿淺水航道中心線運動，船體兩側流場左右對稱。如圖1取動坐標系固結于船體，坐標原點位于船體水線中心，z軸垂直向上，船頭指向x軸正方向，水深為h，自由表面起伏為ζ，船速恒為V。在動坐標系下水流相對于船體以速度V沿x軸負方向運動。

圖1 坐標系Fig.1 Coordinate system

艦船運動引起的流場擾動速度勢Φ應滿足下列方程:

如果不考慮式(8）中第三項 (色散項），則式(8）蛻化為亞臨界航速淺水控制方程 (SSW），即

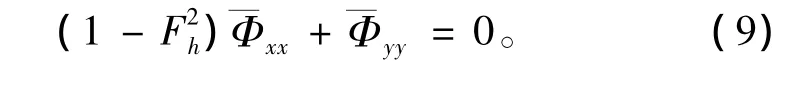
2 理論模型

針對SSW和LTSW方程，結合船體邊界條件以及岸壁條件即可求出滿足相應條件的艦船水壓場理論解。根據薄船假定，船體邊界條件為

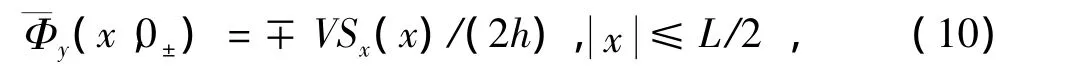
式中:S(x）是船體橫截面面積分布，Sx(x）為S(x）對x求導。

采用數學船型，其橫截面面積分布為

2.1 采用SSW方程

2.1.1 矩形航道

1）源匯分布法

為簡便計，省略表示平均的符號 “—”。艦船以亞臨界航速在淺水中航行時，速度勢Φ應該滿足控制方程式(9）、船體邊界條件式(10）以及岸壁條件式(6）。通過源匯分布法易于求得速度勢Φ，并根據拉格朗日積分求得艦船水壓場水底壓力系數為

根據流場對稱性，取y＞0。對船體邊界條件式以及岸壁條件式進行傅離葉變換，得

2.2 采用LTSW方程

2.2.1 矩形航道

針對無量綱控制方程式(7），省略平均符號“—”和無量綱符號“*”，采用傅離葉積分變換法，分超臨界航速和亞臨界航速2種情況進行求解。

當k在－∞ ～∞間變化時，λ2存在大于和小于2種情況，需要分別討論:

① 當 λ2＞0時，類似超臨界航速求解方法，有

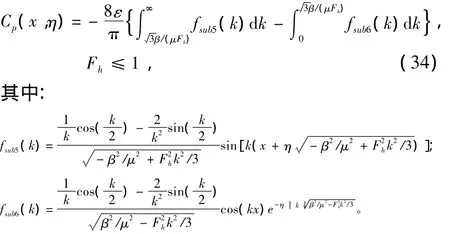
如果γ=0，不計色散效應，則式(33）和式(34）蛻化到SSW方程開闊海域的解。

3 計算結果與分析

基于SSW方程，采用式(19）和式(20）計算淺水開闊海域亞臨界航速艦船水壓場，2種方法 (傅離葉積分變換法和源匯分布法）計算得到的艦船水壓場縱向通過特性曲線符合良好，如圖2所示。由于未計及色散性影響，故計算得到的艦船水壓場負壓區呈現“V”型對稱分布。船首與船尾附近出現正壓峰值，船中下方出現負壓峰值cpmin(cpmin為水底壓力變化的最小壓力系數）。在橫距y=0.1L增大到y=0.5L時，負壓峰值和正壓峰值均減小，但負壓區間寬度呈逐漸增大趨勢。

圖2 2種方法計算結果對比Fig.2 The comparison of two kinds ofmethods

當水深傅汝德數由Fh=0.26逐漸增加到Fh=0.64時，逐漸增大，說明在船中下方產生的水壓信號逐漸明顯，如圖3所示。但在Fh≤0.3時，艦船水壓場縱向通過曲線形狀基本保持不變，說明此時艦船興波對艦船水壓場的影響很小，興波效應可以不予考慮。而當Fh＞0.3時，與Fh關系密切，艦船水壓場需要計及興波影響。

當水深由0.1L逐漸增大至0.5L時，因為水底距離船體變遠，因而迅速減小，說明艦船水

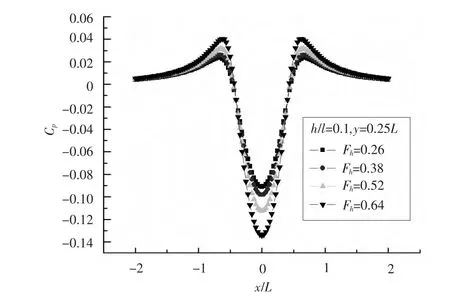
圖3 不同水深傅汝德數下的水壓通過曲線Fig.3 Longitudinal curves of pressure at different Fh

壓場屬于近場，艦船引起的壓力擾動在深度方向衰減較快，如圖4所示。

在矩形航道情況下，為滿足岸壁不可穿透條件，相當于在艦船左右兩側存在一系列艦船鏡像，所有鏡像的貢獻將導致艦船水壓場的負壓峰值比開闊海域的結果要大。當岸壁寬度逐漸增大時，岸壁效應逐漸減弱，逐漸減小，如圖5所示。當w＞5L時，艦船水壓場通過曲線與開闊海域計算結果基本一致，說明此時岸壁影響可以忽略不計。

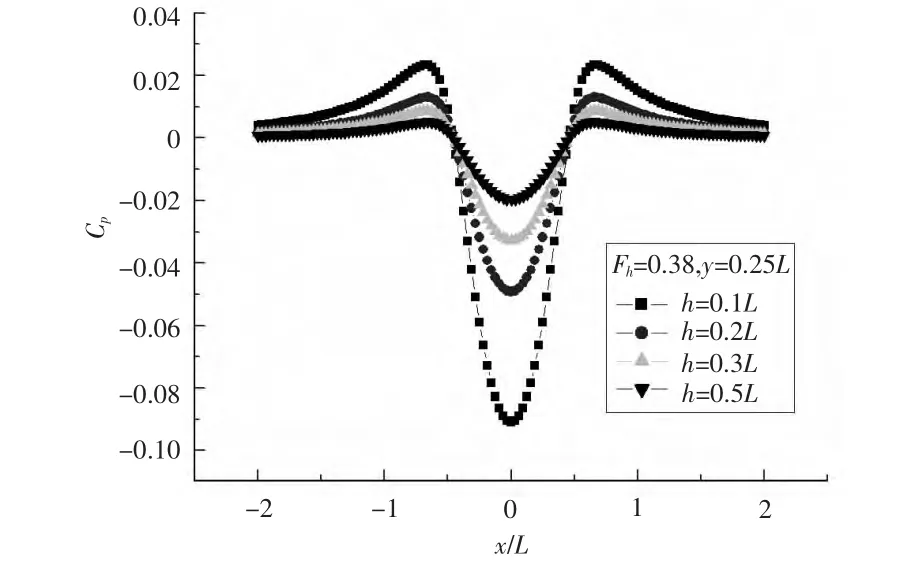
圖4 不同水深下的水壓通過曲線Fig.4 Longitudinal curves of pressure at different depth

圖5 不同寬度下的水壓通過曲線Fig.5 Longitudinal curves of pressure at differentwidth

基于LTSW方程，考慮色散效應，采用式(33）和式(34）計算亞臨界和超臨界航速條件下艦船水壓場的空間分布，如圖6和圖7所示。在h=0.1L及Fh=0.88的亞臨界航速情況下，類似水面興波現象，艦船水壓場分布呈現散波與橫波的特點，艦船水壓場負壓區不再呈現對稱的“V”型分布，而具有明顯的后移特征。當Fh增大時，散波夾角隨之增加，負壓峰值進一步后移，甚至有可能移至船尾之后。當Fh→1時，散波逐漸消失，在船首、船尾附近出現2道明顯的橫波。在h=0.1L及Fh=1.8的超臨界航速情況下，艦船水壓場的橫波逐漸消失，散波逐漸加強，散波夾角隨Fh增加而減小，且壓力系數峰值呈現下降趨勢。

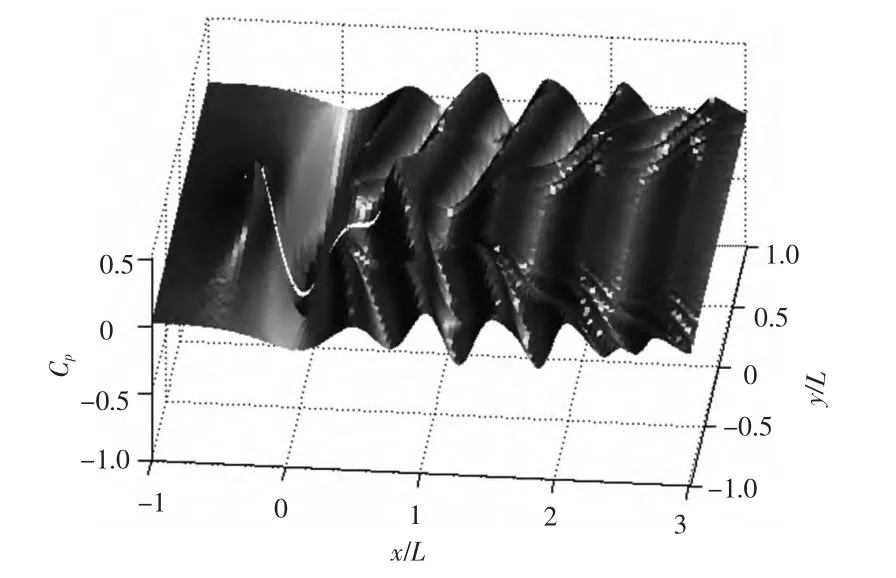
圖6 亞臨界航速艦船水壓場Fig.6 Ship hydrodynamic pressure field at subcritical speed

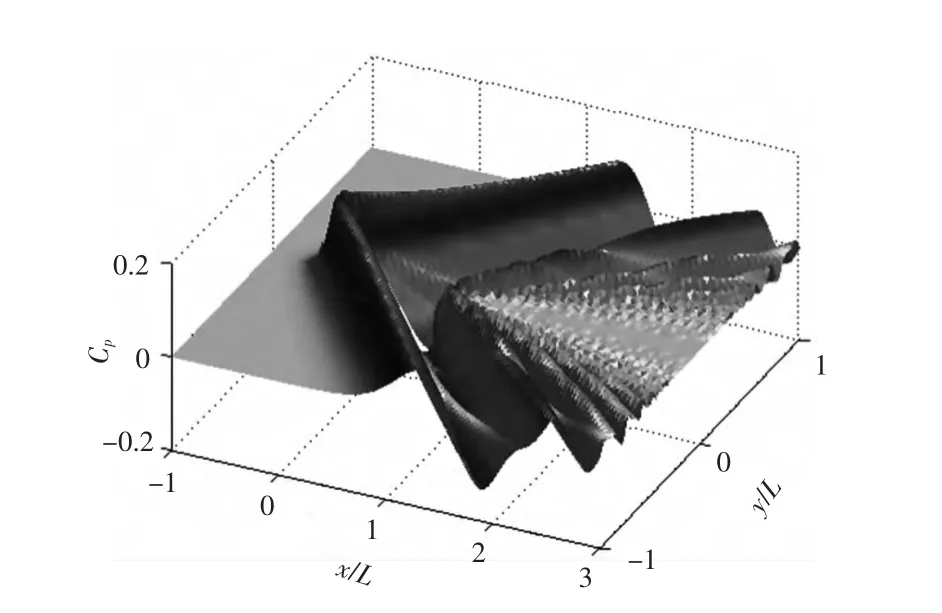
圖7 超臨界航速艦船水壓場Fig.7 Ship hydrodynamic pressure field at supercritical speed

4 結語

基于勢流理論和薄船假定，在開闊海域和矩形航道中建立了基于SSW和LTSW控制方程的淺水艦船水壓場理論模型，采用傅離葉積分變換法獲取了艦船水壓場理論解，并與源匯分布法計算結果進行了比較，驗證所建立模型的正確性和有效性。同時分析了艦船航速、水深、航道寬度、色散效應等因素對艦船水壓場的影響。結論如下:

1）在淺水亞臨界航速條件下，基于SSW控制方程，計算得到的艦船水壓場負壓區呈現對稱的“V”型分布，船首與船尾附近出現正壓峰值，船中下方出現負壓峰值。負壓峰值隨Fh增大而增大，但當Fh≤0.3時，艦船水壓場與Fh基本無關，說明此時艦船興波對水壓場的影響可以忽略。水深對艦船水壓場影響明顯，艦船水壓場隨水深增加衰減較快，說明艦船水壓場屬近場。岸壁的存在相當于艦船系列鏡像的作用，并導致艦船水壓場的負壓峰值增加，但當w＞5L時，岸壁影響可以忽略不計。

2）在淺水開闊海域條件下，基于LTSW方程，考慮色散效應，計算得到的亞臨界和超臨界航速艦船水壓場空間分布具有表面興波的特征。亞臨界航速艦船水壓場負壓區不再是對稱的“V”型分布，而是呈現散波與橫波的特點，并具有明顯的后移特征。在超臨界航速情況下，艦船水壓場的橫波逐漸消失，散波逐漸加強，散波夾角隨Fh增加而減小，且壓力系數峰值呈現下降趨勢。考慮色散性效應時，由于航道中艦船水壓場理論模型中的被積函數存在無限多個不等距奇點，計算較為復雜，留待以后進一步分析和解決。

［1］TUCK E O.Shallow water flows past slender bodies［J］.Fluid Mech，1966(26）:81 －95.

［2］MULLER E.Analysis of the potential flow field and of ship resistance in water of finite depth［J］.I.S.P.，1985(32）:266－277.

［3］SAHIN I，HYMAN M C.Simulation of three-dimensional finite-depth wave phenomenon formoving pressure distributions［J］.Ocean Engineering，2001，28(12）:1621 －1630.

［4］NGUYEN T C.Integral representation of linear free-surface potential flows for bottom pressure calculation［C］.Oceans 2009，MTS/IEEE Biloxi-Marine Technology for Our Future:Global and Local Challenges，2009.

［5］JIANG Tao.Ship waves in shallow Water［R］.Germany:Fortschritt-Berichte VDI，2001.

［6］GOURLAY T P.Flow beneath a ship at small underkeel clearance［J］.Journal of Ship Research，2006，50(3）:250－258.

［7］GOURLAY T P.Slender-body methods for predicting ship squat［J］.Ocean Engineering，2008，35(2）:191 － 200.

［8］黎昆，張志宏，顧建農，等.利用面元法計算艦船在水底引起的壓力分布［J］.海軍工程大學學報，2011，23(1）:43 －46.

LIKun，ZHANG Zhi-hong，GU Jian-nong，et al.Calculating pressure distribution on water bottom caused by a moving ship with panelmothod［J］.Journal of Naval University of Engineering，2011，23(1）:43 －46.

［9］繆濤，張志宏，顧建農，等.面元法求解有限水深船舶興波及水底壓力變化［J］.計算力學學報，2012，29(3）:464－469.

MIAO Tao，ZHANG Zhi-hong，GU Jian-nong，et al.The calculation of ship wave and bottom pressure variation in finite depth by panel method［J］.Chinese Journal of Computational Mechanics，2012，29(3）:464－469.

The theoretical solution and calculation of the hydrodynam ic pressure field of ship in the shallow channel

SUN Bang-bi，ZHANG Zhi-hong，LIU Ju-bin，DENG Hui
(College of Science，Navel University of Engineering，Wuhan 430033，China）

Based on the shallow water wave potential flow theory，at low subcritical speed and linear transcritical speed shallow water wave governing equations were established.According to slender ship assumption，The theoretical solution of hydrodynamic pressure field caused by ship moving at shallow water channelwas obtained by using Fourier integral transform method.The influences ofmoving speed of ship，the wide of channel，depth of water and dispersion effect on the ship hydrodynamic pressure field were analyzed by using numerical simulation，and the resultswere compared with the ones of sources distribution method.Themathematicalmodel and the calculation method were validated.

shallow water;channel;ship;hydrodynamic pressure field;theoretical solution

U661.1

A

1672－7649(2014）04－0011－06

10.3404/j.issn.1672－7649.2014.04.002

2013－06－13;

2013－07－12

國防預研基金資助項目(513030203），海軍工程大學自然科學基金資助項目(HGDQNEQJJ12002）

孫幫碧(1990－），男，碩士研究生，研究方向為艦船水壓場。