基于實(shí)測(cè)地磁數(shù)據(jù)仿真的插值算法適構(gòu)性分析

于運(yùn)治，姜 璐，田茂均

(海軍潛艇學(xué)院，山東 青島 266044）

基于實(shí)測(cè)地磁數(shù)據(jù)仿真的插值算法適構(gòu)性分析

于運(yùn)治，姜 璐，田茂均

(海軍潛艇學(xué)院，山東 青島 266044）

地磁數(shù)據(jù)具有結(jié)構(gòu)性質(zhì)多樣性，使得對(duì)于地磁數(shù)據(jù)插值的研究在不同區(qū)域往往得到不同結(jié)論。針對(duì)此情況，本文提出插值算法的適構(gòu)性概念，并建立基于統(tǒng)計(jì)學(xué)指標(biāo)的算法適構(gòu)性評(píng)價(jià)體系。根據(jù)實(shí)測(cè)地磁數(shù)據(jù)變化劇烈程度的不同劃分5個(gè)實(shí)驗(yàn)區(qū)域;通過等間隔采樣的方式，從原始數(shù)據(jù)中抽取大間隔數(shù)據(jù)作為實(shí)驗(yàn)數(shù)據(jù)，然后算法插值得到估值數(shù)據(jù);圍繞原始數(shù)據(jù)與估值數(shù)據(jù)殘差的集中趨勢(shì)、離散程度和分布形態(tài)等因子，建立基于統(tǒng)計(jì)學(xué)指標(biāo)的算法評(píng)價(jià)體系;仿真驗(yàn)證3種較優(yōu)插值算法的效果。通過對(duì)仿真結(jié)果的定量分析，得出了3種插值算法的適構(gòu)性結(jié)論。

地磁圖;插值算法;統(tǒng)計(jì)學(xué)指標(biāo)

0 引言

地磁數(shù)據(jù)和其他空間數(shù)據(jù)一樣，結(jié)構(gòu)性質(zhì)具有多樣性。因此，地磁數(shù)據(jù)的插值很難找到一種插值算法適用于所有情況，學(xué)者們?cè)谶@方面的研究結(jié)果佐證了這一點(diǎn)。例如張維娜等學(xué)者的研究指出改進(jìn)的謝別得法非常適用于地磁圖插值重構(gòu)［1］。但黃學(xué)功等學(xué)者的研究認(rèn)為徑向基函數(shù)法更適合于其所研究區(qū)域的地磁圖構(gòu)建［2］;而對(duì)于克里金插值法及其衍生模型的研究就更多見。這些都說明對(duì)于不同的研究區(qū)域，由于研究的地磁要素和區(qū)域地磁數(shù)據(jù)空間結(jié)構(gòu)性質(zhì)的不同，研究得出的結(jié)果往往也不盡相同。

由此看來，只研究某一類型區(qū)域的最優(yōu)插值算法，對(duì)于插值加密構(gòu)建地磁匹配基準(zhǔn)圖還是不夠，因?yàn)樗苡锌赡茉谄渌再|(zhì)相異區(qū)域得不到如預(yù)想的效果。總的來說，對(duì)多種類型區(qū)域分別驗(yàn)證數(shù)種插值算法的效果，最終評(píng)價(jià)得出各種插值算在不同地磁數(shù)據(jù)情況中的效果十分必要。針對(duì)這一需要，這里提出了插值算法的適構(gòu)性概念。其中，插值算法適構(gòu)性是指:插值算法對(duì)地磁圖插值構(gòu)建的適應(yīng)能力，地磁基準(zhǔn)圖的實(shí)測(cè)法構(gòu)建以最大限度的接近自然真值為目的，而插值算法的插值反演以最大限度接近實(shí)測(cè)值為宗旨。文章圍繞評(píng)價(jià)各插值算法的適構(gòu)性展開，最后定性得出各類型區(qū)域的最優(yōu)插值算法。

1 算法原理

插值算法在許多工程領(lǐng)域都得到了大量運(yùn)用，典型的如最小曲率法、樣條函數(shù)法、多元回歸法、數(shù)據(jù)度量法等［3－4］。而在地理數(shù)據(jù)的插值研究中，反距離加權(quán)法、改進(jìn)的謝別得法、克里金法、徑向基函數(shù)法、局部多項(xiàng)式法、自然鄰點(diǎn)法等的應(yīng)用則較為普遍［5］。經(jīng)過筆者前一階段的研究發(fā)現(xiàn)克里金法、徑向基函數(shù)法、局部多項(xiàng)式法在海洋地磁數(shù)據(jù)的插值處理中有較好的表現(xiàn)，本文插值算法適構(gòu)性的分析即針對(duì)這3種方法而展開。

1.1 克里金法

克里金 (Kriging）插值法是一種空間自協(xié)方差最優(yōu)內(nèi)插算法，實(shí)質(zhì)是利用區(qū)域化變量的原始數(shù)據(jù)和變異函數(shù)的結(jié)構(gòu)特點(diǎn)，對(duì)未知樣點(diǎn)進(jìn)行線性無偏、最優(yōu)估計(jì)。它一方面通過距離對(duì)已知樣本點(diǎn)賦權(quán)重來計(jì)算未知點(diǎn)的值;另一方面又通過變異函數(shù)的引入來考慮已知點(diǎn)與未知點(diǎn)的空間關(guān)系。克里金法常采用的變異函數(shù)模型有常數(shù)模型、指數(shù)模型、球狀模型、高斯模型等［6］。算法原理如下:

對(duì)于研究區(qū)域A，設(shè)在區(qū)域內(nèi)采樣的位置坐標(biāo)為Xi，變量的觀測(cè)值為 Z(Xi），i=1，2，3，…，n，則預(yù)測(cè)點(diǎn)X0的估計(jì)值Z^(X0）可用這n個(gè)樣本點(diǎn)的線性組合來表示:

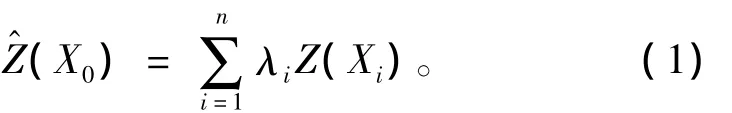
其中λi為已測(cè)量點(diǎn)Z(Xi）的權(quán)系數(shù)。上式中權(quán)系數(shù)的確定由克里金方程組決定，方程組可表示為:

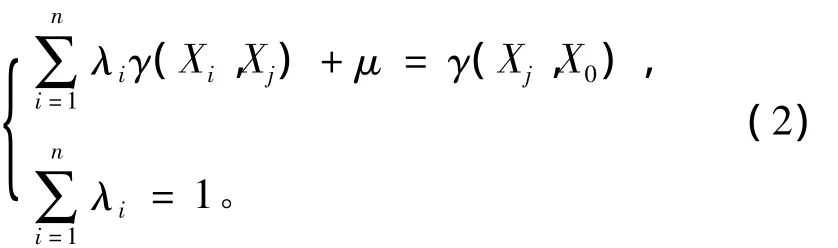
式中:γ(Xi，Xj）為磁測(cè)量點(diǎn)的變異函數(shù)，μ為拉格朗日系數(shù)。本文采用的變異函數(shù)為克里金立方模型。

1.2 局部多項(xiàng)式法

多項(xiàng)式插值也是常用的插值方法之一，有著廣泛應(yīng)用。但在進(jìn)行多項(xiàng)式插值時(shí)，要找到一個(gè)適合的函數(shù)模型不那么容易，而且當(dāng)多項(xiàng)式的階數(shù)較高時(shí)，其波動(dòng)加大，運(yùn)算時(shí)間也加長。因此，衍生出了局部多項(xiàng)式法 (local polynomial，LP）。局部多項(xiàng)式法是一種局部加權(quán)最小二乘方法，即對(duì)插值對(duì)象給定一搜索域，然后根據(jù)適當(dāng)?shù)奶囟A數(shù)的多項(xiàng)式函數(shù)插值出待插值點(diǎn)的值。局部多項(xiàng)式插值產(chǎn)生的曲面主要依賴于區(qū)域化變量的局部變異。其主要采用的多項(xiàng)式有一次、二次和三次多項(xiàng)式［7］。

1.3 徑向基函數(shù)法

徑向基函數(shù)法 (radial basis function，RBF）是一種精確的插值方法，適用于對(duì)大量點(diǎn)數(shù)據(jù)進(jìn)行插值計(jì)算，從而獲得平滑表面，且能預(yù)測(cè)比樣點(diǎn)高或低的未知點(diǎn)的值，因而具有較高的預(yù)測(cè)精度，能較好地反應(yīng)數(shù)據(jù)變化情況。它首先將插值函數(shù)構(gòu)造成下面形式的空間點(diǎn)函數(shù):

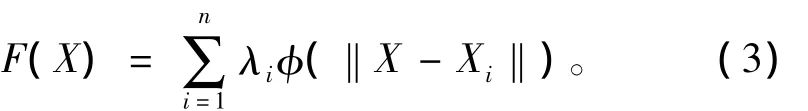
式中:X=(x，y，z），Xi為已知點(diǎn) (i=1，2，…，n）;λi為待定系數(shù);φ為指定的基函數(shù);‖·‖為歐氏范數(shù)。然后權(quán)系數(shù)的求解可以用已知數(shù)據(jù)點(diǎn)的值通過插值設(shè)定的條件確定。

影響徑向基函數(shù)法插值精度關(guān)鍵是基函數(shù)的確定，常用的有逆二次曲面、二次曲面、自然三次樣條、Gauss函數(shù)、復(fù)二次函數(shù)、倒轉(zhuǎn)復(fù)二次函數(shù)、薄板樣條函數(shù)［8］。本文采用復(fù)二次函數(shù)。

2 算法仿真實(shí)驗(yàn)

2.1 仿真實(shí)驗(yàn)數(shù)據(jù)

數(shù)據(jù)來源于某單位在某海區(qū)科研課題所采集的磁異常數(shù)據(jù)。涉及到數(shù)據(jù)保密性等原因去掉了經(jīng)緯度而改為絕對(duì)距離。為驗(yàn)證算法在不同數(shù)據(jù)變化區(qū)域的效果，依據(jù)該區(qū)域磁異常變化的劇烈程度確立了5個(gè)實(shí)驗(yàn)區(qū)。其中實(shí)驗(yàn)區(qū)1數(shù)據(jù)的特點(diǎn)是變化幅度大，程度相對(duì)劇烈;實(shí)驗(yàn)區(qū)2數(shù)據(jù)特點(diǎn)是變化幅度較大，程度非常劇烈;實(shí)驗(yàn)區(qū)3數(shù)據(jù)則變化幅度小，劇烈程度較弱;實(shí)驗(yàn)區(qū)4數(shù)據(jù)變化最為平緩;實(shí)驗(yàn)區(qū)5是包含上述4個(gè)實(shí)驗(yàn)區(qū)的一個(gè)大區(qū)，作為不確定數(shù)據(jù)變化劇烈程度的區(qū)域存在。實(shí)驗(yàn)區(qū)原始數(shù)據(jù) (50 m精度）三維圖如圖1～圖4所示。

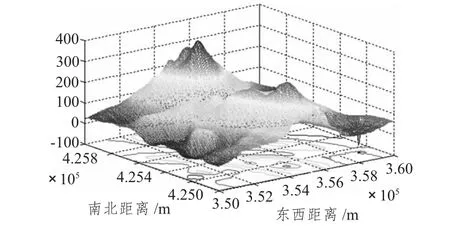
圖1 實(shí)驗(yàn)區(qū)1磁異常三維圖Fig.1 Experimental zone 1 magnetic anomalies in three-dimensionalmap

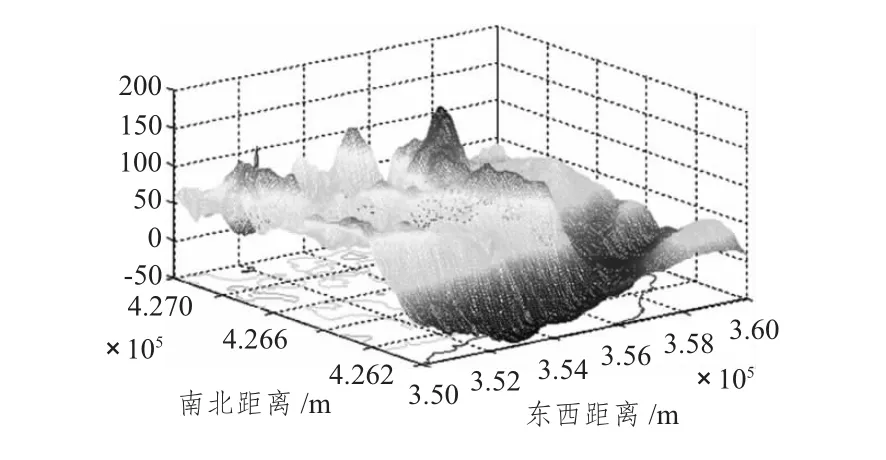
圖2 實(shí)驗(yàn)區(qū)2磁異常三維圖Fig.2 Experimental zone 2 magnetic anomalies in three-dimensionalmap

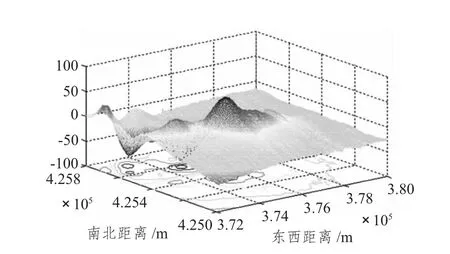
圖3 實(shí)驗(yàn)區(qū)3磁異常三維圖Fig.3 Experimental zone 3 magnetic anomalies in three-dimensionalmap

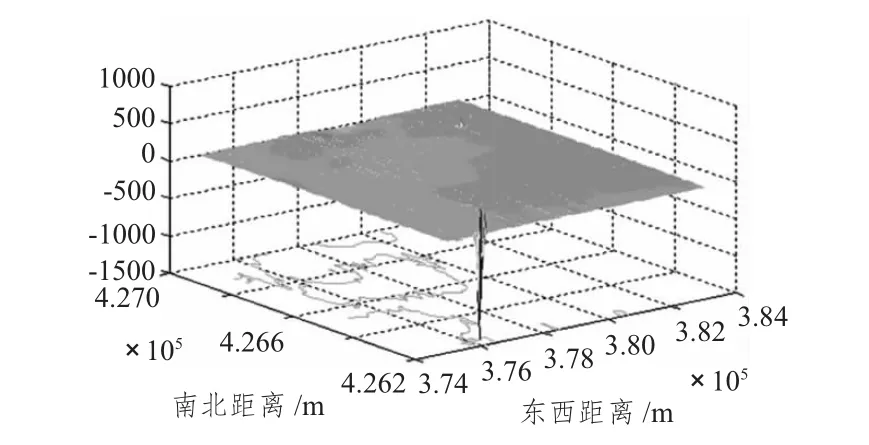
圖4 實(shí)驗(yàn)區(qū)4磁異常三維圖Fig.4 Experimental zone 4 magnetic anomalies in three-dimensionalmap

實(shí)驗(yàn)區(qū)5范圍較大，且是綜合上述4個(gè)區(qū)域的綜合區(qū)，因此不再圖示說明。

2.2 算法評(píng)價(jià)體系

1）評(píng)價(jià)方法

算法評(píng)價(jià)是將部分已知屬性值的樣本點(diǎn)作為“訓(xùn)練數(shù)據(jù)集”(占原始數(shù)據(jù)量的1%）用于算法插值計(jì)算;將原始所有數(shù)據(jù)點(diǎn)作為“驗(yàn)證數(shù)據(jù)集”存在。然后利用“訓(xùn)練數(shù)據(jù)集”樣本點(diǎn)進(jìn)行插值計(jì)算，將得出的插值結(jié)果與“驗(yàn)證數(shù)據(jù)集”中的點(diǎn)測(cè)量值對(duì)比得出插值算法殘差;最后運(yùn)用各定量評(píng)價(jià)指標(biāo)比較各插值算法的適構(gòu)性。文章采取等間隔采樣的方式 (由于目前大部分海上測(cè)量都采用的是等間隔）確定等間隔500 m的點(diǎn)作為訓(xùn)練數(shù)據(jù)集，原始50 m精度的點(diǎn)作為驗(yàn)證數(shù)據(jù)集。

2）定量評(píng)價(jià)指標(biāo)

評(píng)價(jià)指標(biāo)確立從2方面考慮，一是算法的運(yùn)算時(shí)間;二是殘差的性質(zhì)。對(duì)殘差性質(zhì)的分析目前還是以統(tǒng)計(jì)學(xué)指標(biāo)定量評(píng)價(jià)為主，為此本文從數(shù)據(jù)集中趨勢(shì)、離散程度和分布形態(tài)3個(gè)方面確定均值、平均絕對(duì)差、全距、標(biāo)準(zhǔn)差、峰度和偏態(tài)等6個(gè)統(tǒng)計(jì)學(xué)指標(biāo)，再加上運(yùn)算時(shí)間共計(jì)7個(gè)定量評(píng)價(jià)指標(biāo)。指標(biāo)表示如下［9－10］:

2.3 仿真結(jié)果與分析

1）各插值算法仿真驗(yàn)證指標(biāo)值

各插值算法仿真驗(yàn)證指標(biāo)值如表1～表5所示。

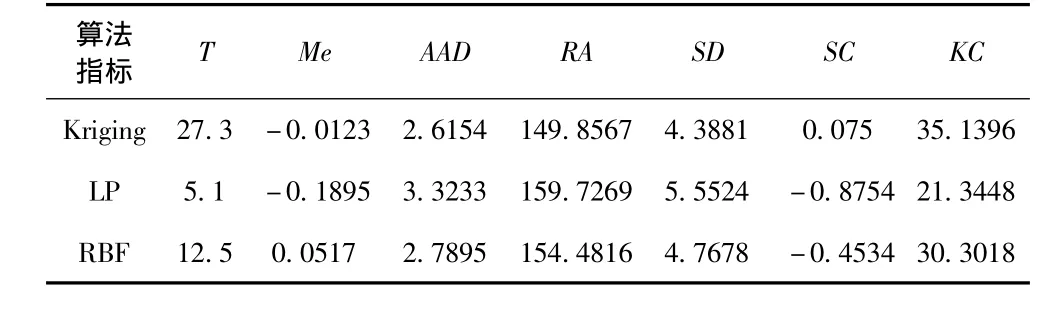
表1 實(shí)驗(yàn)區(qū)1指標(biāo)值Tab.1 Experimental zone 1 indicator value table

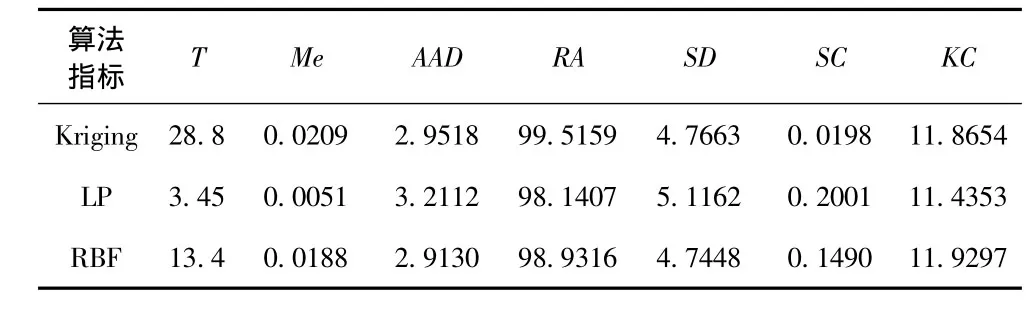
表2 實(shí)驗(yàn)區(qū)2指標(biāo)值Tab.2 Experimental zone 2 indicator value table

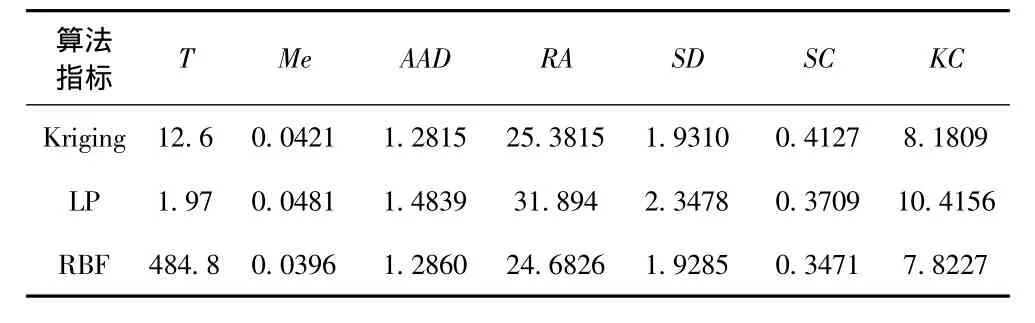
表3 實(shí)驗(yàn)區(qū)3指標(biāo)值Tab.3 Experimental zone 3 indicator value table

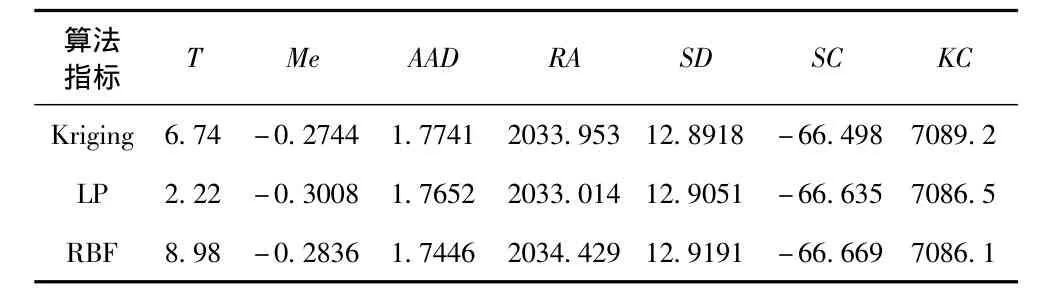
表4 實(shí)驗(yàn)區(qū)4指標(biāo)值Tab.4 Experimental zone 4 indicator value table

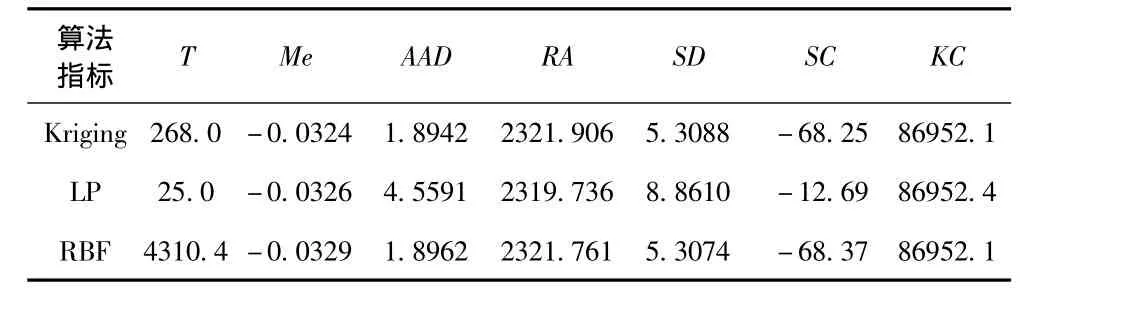
表5 實(shí)驗(yàn)區(qū)5指標(biāo)值Tab.5 Experimental zone 5 indicator value table

2）分析結(jié)論

從實(shí)驗(yàn)區(qū)1可看出，克里金法與真值的偏差、數(shù)據(jù)離散程度、極距等都最小，且分布形態(tài)也較為合適，唯一不足的是時(shí)效性太差;徑向基函數(shù)法與克里金法效果接近，而且在時(shí)效性上優(yōu)于克里金法;而局部多項(xiàng)法則在時(shí)效性上占了優(yōu)勢(shì)。

實(shí)驗(yàn)區(qū)2結(jié)果反映出徑向基函數(shù)法平均絕對(duì)差、標(biāo)準(zhǔn)差、以及運(yùn)算時(shí)間3個(gè)重要指標(biāo)上都占了優(yōu)勢(shì)，而且分布形態(tài)也較為理想，適構(gòu)性最好。另外2個(gè)次之。

實(shí)驗(yàn)區(qū)3雖然徑向基函數(shù)法在絕對(duì)差、標(biāo)準(zhǔn)差等重要指標(biāo)上都最好，但是其時(shí)效性太差，而各指標(biāo)和它接近的克里金法時(shí)效性適中，適構(gòu)性最優(yōu)。

實(shí)驗(yàn)區(qū)4中方法的效果除了運(yùn)算時(shí)間外，差別非常小;而參考運(yùn)算時(shí)間來看局部多項(xiàng)式法適構(gòu)性最佳。

實(shí)驗(yàn)區(qū)5反映出的結(jié)果和實(shí)驗(yàn)區(qū)3相似，綜合來看克里金法適構(gòu)性優(yōu)于另外2個(gè)。

綜合上述5個(gè)實(shí)驗(yàn)區(qū)的分析結(jié)果可得出結(jié)論;在海洋地磁數(shù)據(jù)的插值處理中，如果不明確數(shù)據(jù)變化的劇烈程度應(yīng)當(dāng)優(yōu)先采用克里金法;而明確數(shù)據(jù)變化程度特別劇烈時(shí)應(yīng)當(dāng)采用徑向基函數(shù)法;變化緩慢時(shí)優(yōu)先考慮局部多項(xiàng)式法。

3 結(jié)語

由于海洋地磁數(shù)據(jù)獲取的困難性，要獲得高精度、高密度的地磁數(shù)據(jù)非常困難。然而，隨著目前地磁匹配導(dǎo)航應(yīng)用于水下潛航器導(dǎo)航研究的發(fā)展。對(duì)于地磁圖網(wǎng)格精度的要求卻在逐漸提高，針對(duì)這一矛盾，插值算法的引入是解決困境的關(guān)鍵技術(shù)之一。但是插值算法眾多，地磁數(shù)據(jù)的結(jié)構(gòu)特性也各異，因此為選擇合適的插值算法給出一定參考準(zhǔn)則十分必要。本文研究了3種插值算法在數(shù)個(gè)地磁變化情況不同區(qū)域的效果，以適構(gòu)性作為算法選取準(zhǔn)則的核心做了仿真驗(yàn)證，并得出了克里金法、局部多項(xiàng)式法和徑向基函數(shù)法的適構(gòu)性結(jié)論。雖然本文的研究取得了一定的成果，但是諸多方面還有待進(jìn)一步研究。由于海上數(shù)據(jù)測(cè)量的困難性，所能提供的實(shí)測(cè)數(shù)據(jù)有限，要更好的評(píng)價(jià)算法的適構(gòu)性，就需要大量的實(shí)測(cè)數(shù)據(jù)作為實(shí)驗(yàn)數(shù)據(jù)或者佐證數(shù)據(jù)。這一方面還需要進(jìn)一步的拓展。

［1］黃學(xué)功，房建成，劉剛，等.地磁圖制備方法及其有效性評(píng)估［J］.北京航空航天大學(xué)學(xué)報(bào)，2009，35(7）:891－894.

HUANG Xue-gong，F(xiàn)ANG Jian-cheng，LIU Gang，et al.Geomagneticmapping and validity estimation［J］.Journal of Beijing Universiy of Aeronautics and Astronautics，2009，35(7）:891－894.

［2］張維娜，呂云霄，吳美平.改進(jìn)謝別德插值方法在地磁圖構(gòu)建中的應(yīng)用［J］.導(dǎo)航與控制，2011，2(10）:28－32.

ZHANGWei-na，LV Yun-xiao，WU Mei-ping.Application ofmodified shepard interpolation in geomaglletic map［J］.Navigation and Control，2011，10(2）:28 －32.

［3］喬玉坤，王仕成，張金生，等.區(qū)域地磁場(chǎng)建模主要方法及其在地磁導(dǎo)航基準(zhǔn)圖構(gòu)建中的應(yīng)用［C］.第五屆國家安全與軍事地球物理學(xué)術(shù)研討會(huì)論文集，2009.

QIAO Yu-kun，WANG Shi-cheng，ZHANG Jin-sheng.Regional geomagnetic field modeling method and its geomagnetic navigation reference map building［C］.Conference Proceedings of the Fifth National Security and Military Geophysical，2009.

［4］王哲，王仕成，張金生，等.一種地磁匹配制導(dǎo)基準(zhǔn)圖制備方法及其有效性評(píng)價(jià)［J］.系統(tǒng)工程與電子技術(shù)，2008，30(11）:2207 －2211.

WANG Zhe，WANG Shi-cheng，ZHANG Jin-sheng，et al.Method for preparation of reference map in geomagnetism matching guidance and its validity evaluation［J］.Systems Engineering and Electronics，2008，30(11）:2207 －2211.

［5］朱會(huì)義，劉述林，賈紹鳳.自然地理要素空間插值的幾個(gè)問題［J］.地理研究，2004，23(4）:425 －432.

ZHU Hui-yi，LIU Shu-lin，JIA Shao-feng.Problems of the spatial interpolation of physical geographical elements［J］.Geographical Research，2004，23(4）:425 －432.

［6］白世彪，王建，常直楊.Surfer10地學(xué)計(jì)算機(jī)制圖［M］.北京:科學(xué)技術(shù)出版社，2012:217－220.

BAI Shi-biao，WANG Jian，CHANG Zhi-yang.Surfer10 geoscience computer graphics［M］.Beijing:Science and Technology Press，2012:217 －220.

［7］汪俊，高金耀，吳招才，等.局部多項(xiàng)式插值方法在多源海底沉積厚度數(shù)據(jù)融合中的應(yīng)用［J］.海洋科學(xué)，2009(4）:25－28.

WANG Jun，GAO Jin-yao，WU Zhao-cai，et al.The local polynomials fitting methods on geospatial data merging:an application to the multi-resources marine sediment thickness data［J］.Marine Sciences，2009(4）:25 － 28.

［8］繆報(bào)通，陳發(fā)來.徑向基函數(shù)神經(jīng)網(wǎng)絡(luò)在散亂數(shù)據(jù)插值中的應(yīng)用［J］.中國科學(xué)技術(shù)大學(xué)學(xué)報(bào)，2001，31(2）:135－142.

MIAO Bao-tong，CHEN Fa-lai.Applications of radius basis function neural networks in scattered data interpolation［J］.Journal of University of Science and Technology of China，2001，31(2）:135 －142.

［9］賈俊平，何曉群，金勇進(jìn).統(tǒng)計(jì)學(xué)［M］.北京:中國人民大學(xué)出版社，2000:212－219.

JIA Jun-ping，HE Xiao-qun，JIN Yong-jin.Statistics［M］.Beijing:China Renmin University Press，2000:212 －219.

［10］杜智敏.抽樣調(diào)查與SPSS應(yīng)用［M］.北京:電子工業(yè)出版社，2010:471－485.

DU Zhi-min.Sample survey and SPSS applications［M］.Beijing:Publishing House of Electronics Industry，2010:471－485.

［11］王孝玲.教育統(tǒng)計(jì)學(xué)(2版）［M］.上海:華東師范大學(xué)出版社，2001:290－307.

WANG Xiao-ling.Educational statistics(2 edition）［M］.Shanghai:East China Normal University Press，2001:290－307.

Analysis of interpolation suitability of algorithm based on simulation of themeasured geomagnetic data

YU Yun-zhi，JIANG Lu，TIAN Mao-jun
(Navy Submarine Academy，Qingdao 266044，China）

The structural properties diversity of the geomagnetic data，make for geomagnetic data interpolation research in different areas often get different conclusions.In view of this situation，this paper puts forward the optimal structure concept of the interpolation algorithm，and to establish the interpolation suitability of algorithm evaluation system based on the statistical indicators.Firstly，the paper based on different change intensity of the geomagnetic data has division of the five experimental area;Secondly，through the way such as sampling interval，extract big interval data from the original data as experimental data，and use the interpolation algorithm gets valuation data;Thirdly，around the original data and valuation data residual concentration trend，discrete degree and distribution form factors，this paper build the interpolation suitability of algorithm evaluation system based on statistics index;Finally，take advantage of simulation results show the effectof three better interpolation algorithm.Based on the quantitative analysis of the simulation results，it is concluded that interpolation suitability of algorithm conclusion of the three kinds of interpolation algorithm.

geomagnetic mapping;interpolation method;statistical indicators

U666.1

A

1672－7649(2014）05－00130－05

10.3404/j.issn.1672－7649.2014.05.027

2013－01－29;

2013－03－18

于運(yùn)治(1964－），男，高級(jí)工程師，主要從事潛艇導(dǎo)航方面研究。