基于ARMAX模型的集中供熱系統(tǒng)負(fù)荷預(yù)測研究

魏延寶，林紅權(quán)，馬增良，王學(xué)雷

（中國科學(xué)院自動化研究所，北京100190）

近年來集中供熱的規(guī)模不斷擴(kuò)大，用戶對供熱質(zhì)量的要求也不斷提高，實現(xiàn)按需供熱、均勻供熱成為亟待解決的關(guān)鍵問題[1]。集中供熱系統(tǒng)中各自動控制子系統(tǒng)的給定值都是由預(yù)報負(fù)荷決定的，因此實現(xiàn)及時準(zhǔn)確的負(fù)荷預(yù)測是提高供熱質(zhì)量的前提和基礎(chǔ)。對于制定能源規(guī)劃、提高供熱系統(tǒng)能源利用效率、保護(hù)環(huán)境具有重要意義[2]。

供熱負(fù)荷是指在某一室外溫度下，為達(dá)到要求的室內(nèi)溫度，供熱系統(tǒng)在單位時間內(nèi)向建筑物供給的熱量[3]。由于供熱系統(tǒng)內(nèi)導(dǎo)熱介質(zhì)以及建筑物的熱慣性、遲滯等特點，室外風(fēng)速、太陽輻射、建筑物結(jié)構(gòu)以及使用情況等因素影響也比較復(fù)雜，通過機(jī)理方法建立準(zhǔn)確的負(fù)荷預(yù)測模型非常困難。近些年來，國內(nèi)外專業(yè)人士針對這一問題也提出了許多解決方法，如回歸預(yù)測和神經(jīng)網(wǎng)絡(luò)等。回歸預(yù)測方法計算簡單，但模型精度較低；神經(jīng)網(wǎng)絡(luò)方法盡管精度很高，但所需數(shù)據(jù)多且容易陷入局部極小，同時網(wǎng)絡(luò)結(jié)構(gòu)的確定有很強(qiáng)的主觀性，因此并不令人滿意[4-6]。本文采用時間序列分析方法，利用熱負(fù)荷的歷史數(shù)據(jù)，并充分考慮外界因素的影響，能夠在短時間內(nèi)建立預(yù)測模型并以較高的精度對未來時刻的熱負(fù)荷進(jìn)行預(yù)測。

ARMAX擴(kuò)展自回歸滑動平均模型（extended auto-regressive moving average）能夠準(zhǔn)確地描述動態(tài)過程，在電力系統(tǒng)以及計量經(jīng)濟(jì)等領(lǐng)域都有著廣泛的應(yīng)用[7]。利用ARMAX模型預(yù)測供熱系統(tǒng)熱負(fù)荷，通過對歷史數(shù)據(jù)的統(tǒng)計和分析尋找熱負(fù)荷的變化規(guī)律。本文對ARMAX模型進(jìn)行了詳細(xì)的介紹，并采用最小二乘法進(jìn)行了參數(shù)估計。通過對熱負(fù)荷數(shù)據(jù)進(jìn)行統(tǒng)計和分析，得到了鍋爐供水溫度預(yù)測模型。經(jīng)對比，預(yù)測結(jié)果在短期內(nèi)具有較高的精度。

1 ARMAX模型介紹

當(dāng)系統(tǒng)中某一因變量的時間序列數(shù)據(jù)沒有確定的變化形式，也不能用時間的確定函數(shù)描述時，可以用概率統(tǒng)計的方法尋求比較合適的隨機(jī)模型近似反映其變化規(guī)律。ARMAX模型是一種典型的描述離散時間序列的工具，其結(jié)構(gòu)上由AR模型、MA 模型及回歸項 3 部分結(jié)合構(gòu)成。 （p，r，q）階ARMAX模型的數(shù)學(xué)表達(dá)式如下：

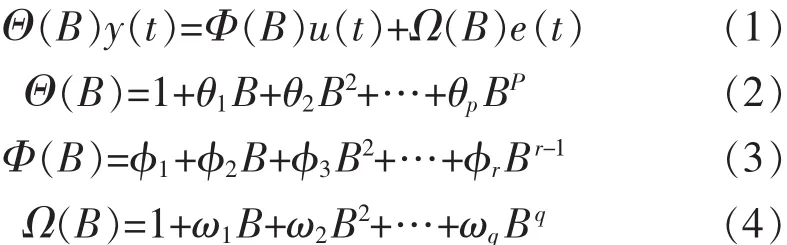
其中：p、q、r分別是自回歸、滑動平均以及回歸項的階數(shù)；θi（i=1…p）、φj（j=1…r）和 wk（k=1…q）是模型的待定系數(shù)；et是均值為零方差不為零的白噪聲序列。模型輸出yt為平穩(wěn)的時間序列，ytyt-1…yt-m是該序列不同時刻的隨機(jī)變量值，反映時間的滯后關(guān)系。B為一階后移算子，滿足：

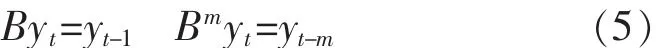
ARMAX模型融合了AR模型和MA模型的特點，通過對過去的觀測值、現(xiàn)在的干擾值以及過去的干擾值線性組合進(jìn)行預(yù)測。與傳統(tǒng)的ARMA相比，通過引入與輸出序列相關(guān)的另一序列作為回歸項，模型的準(zhǔn)確性及魯棒性更高。利用ARMA模型解決問題的一般步驟如圖1所示，核心環(huán)節(jié)是序列平穩(wěn)化及模型參數(shù)的求取，將在下面的相應(yīng)章節(jié)中作詳細(xì)介紹。

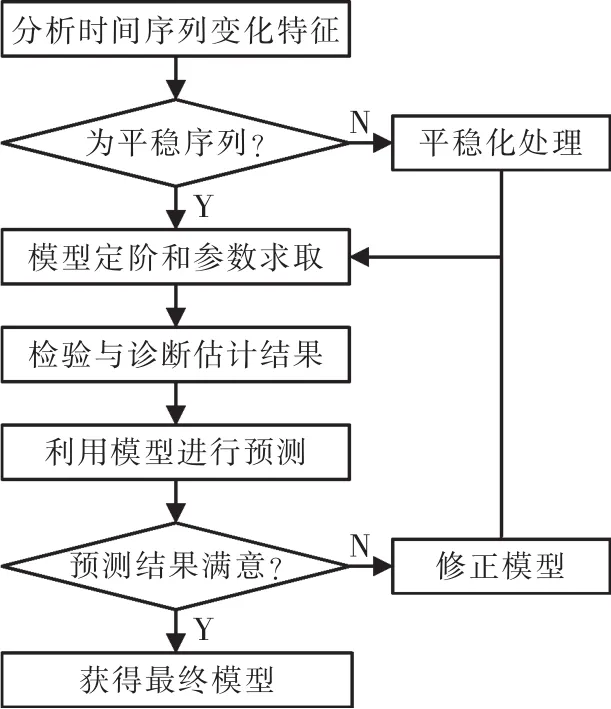
圖1 建立ARMAX模型流程圖Fig.1 Flow chart of establishing ARMAX model

2 序列平穩(wěn)性分析

進(jìn)行時間序列模型估計，前提是滿足序列是非隨機(jī)且平穩(wěn)的條件。若隨機(jī)，序列的前后觀察值之間無任何關(guān)系，則沒有任何信息可以提取；若非平穩(wěn)，即序列變化特征隨時間推移而改變，這樣即便找到變化規(guī)律，也無法用于預(yù)測。

隨機(jī)性可以通過序列的自相關(guān)系數(shù)來判斷，若存在非0，則證明該序列是非隨機(jī)的，反之則為隨機(jī)序列；平穩(wěn)性的判斷有多種方法，可以通過相關(guān)圖法利用時間序列的相關(guān)圖衰減特性進(jìn)行判斷，也可以通過單位根檢驗利用統(tǒng)計檢驗的方法進(jìn)行判斷。

對于非平穩(wěn)序列，為了滿足利用ARMAX模型建模的條件，可以進(jìn)行d階（d一般不超過2）差分使非平穩(wěn)時間序列平穩(wěn)化[8]。為此，首先定義一個差分算子Δ＝1-B，滿足：

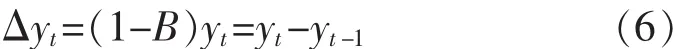
這樣就可以將非平穩(wěn)序列轉(zhuǎn)化為平穩(wěn)序列再進(jìn)行估計和建模。綜合上述分析，得到了經(jīng)差分后平穩(wěn)的d階ARMAX模型，結(jié)構(gòu)如下：

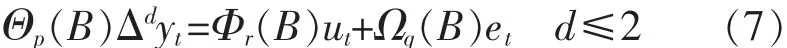
集中供熱系統(tǒng)根據(jù)被控變量的不同有不同的控制運(yùn)行方式，如控制供回水差壓為主的運(yùn)行方式和控制供水溫度為主的運(yùn)行方式。已知中關(guān)村某供暖公司采用調(diào)節(jié)供水溫度和運(yùn)行時間的方式調(diào)節(jié)熱負(fù)荷，指導(dǎo)司爐作業(yè)和供熱運(yùn)行，供水流量不作頻繁調(diào)節(jié)。因此，本文針對這一控制供水溫度為主的集中供熱系統(tǒng)，將鍋爐供水溫度作為分析和預(yù)測的對象，根據(jù)SCADA系統(tǒng)采集到的2012年11月份的供水溫度數(shù)據(jù)繪制出時序圖，數(shù)據(jù)采集周期為每小時 1次，如圖 2（a）所示。

通過對供熱系統(tǒng)時序圖的分析不難發(fā)現(xiàn)，供水溫度的變化是非平穩(wěn)過程，具有一定的增長趨勢和周期性。經(jīng)過分析，在對數(shù)據(jù)進(jìn)行了一階差分及平移處理后得到了一個平穩(wěn)且非白噪聲的時間序列，如圖 2（b）所示。

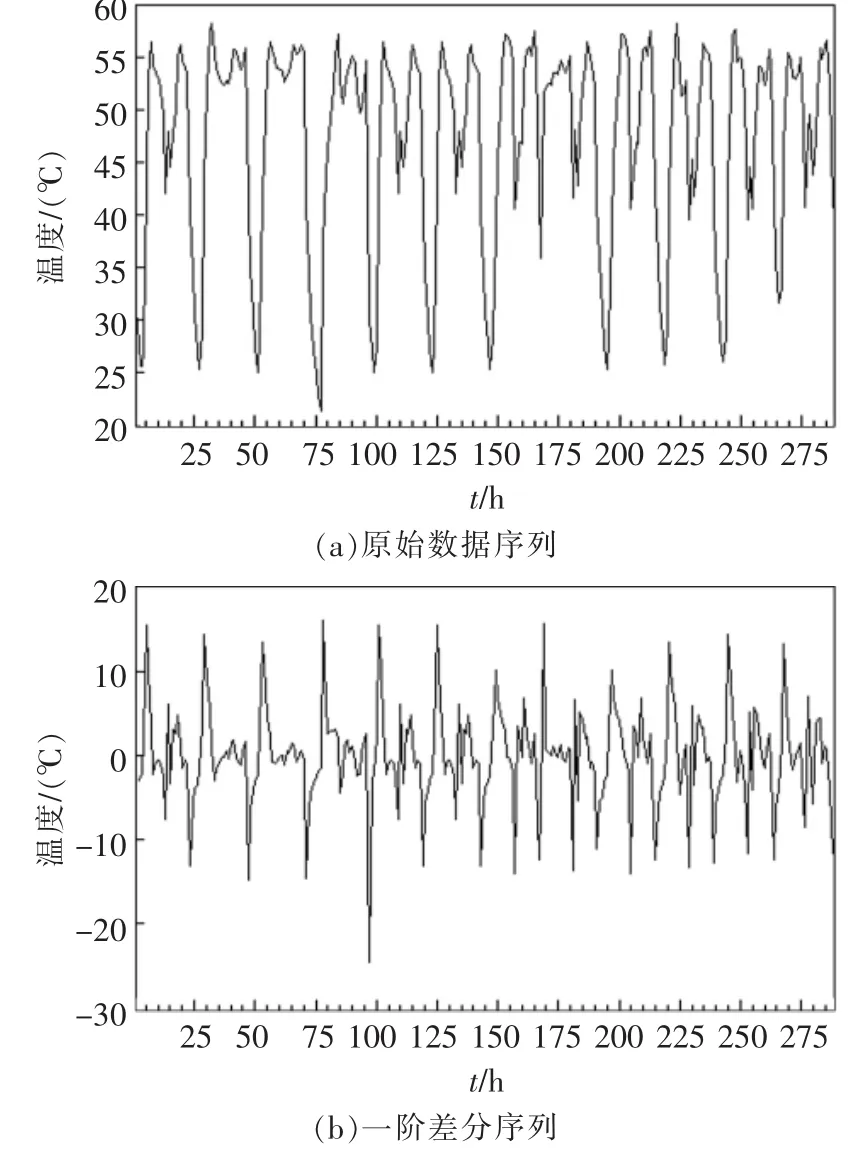
圖2 熱負(fù)荷溫度時間序列圖Fig.2 Time series of load temperature

3 ARMAX模型參數(shù)求取

ARMAX模型參數(shù)的求取包含兩方面內(nèi)容，階次的確定以及模型參數(shù)的估計。

3.1 模型階次的確定

模型的階次通過檢驗變量的自相關(guān)函數(shù)和偏相關(guān)函數(shù)來確定。按照定義，列出時間序列yt（t=1…N）的統(tǒng)計特性參數(shù)如下：

均值μy和方差σy2分別為

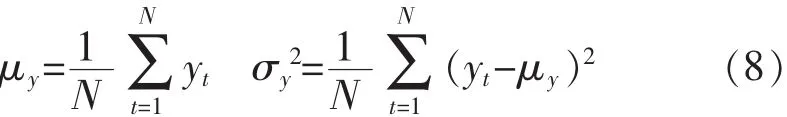
由此，得到協(xié)方差 Cov（yt，yt+k）和自相關(guān)函數(shù) ρk：

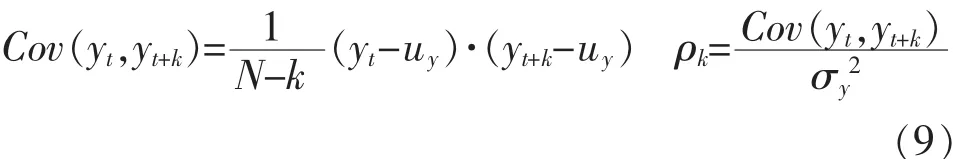
偏相關(guān)函數(shù)Φ的定義為

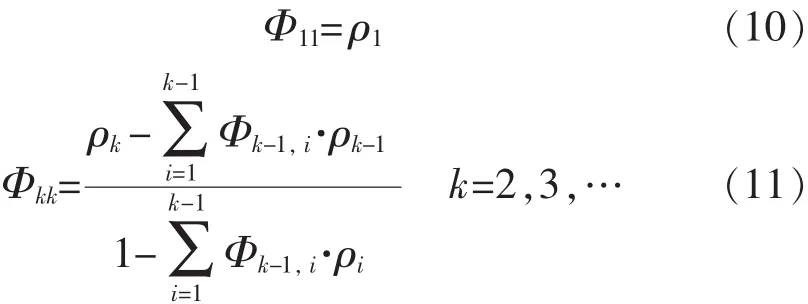
Φk，i=Φk-1，i-Φkk·Φk-1，k-ik=1，2，3，…k-1 （12）

對于AR模型，序列滿足偏相關(guān)函數(shù)滯后期截尾這一特性。即對于p階的AR模型，自相關(guān)函數(shù)滿足：

所以當(dāng)求出使偏自相關(guān)系數(shù)為0時的k值，可以得到模型的自回歸階次k-1。

而對于MA模型，自相關(guān)系數(shù)是截尾的，其性質(zhì)和AR模型類似。對于q階的MA模型，當(dāng)?shù)玫阶韵嚓P(guān)系數(shù)為0時的k值，可以確定MA模型的階次為k-1。根據(jù)以上對于AR和MA模型的特性分析，可以大致得到p和q的數(shù)值，關(guān)于輸入階次r的確定，應(yīng)本著靈活性和節(jié)儉性的原則，既要滿足模型通用性又不至于使運(yùn)算過于復(fù)雜[9]。

3.2 模型參數(shù)的估計

線性回歸模型參數(shù)估計最常用的方法是最小二乘法，可以按下面的方式進(jìn)行數(shù)學(xué)描述。

當(dāng)數(shù)學(xué)模型有下面的形式時：

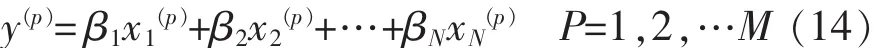
式中：y（p）為模型擬合變量；x1（p），x2（p），…，xN（p）為影響預(yù)測結(jié)果的因變量；β1，β2， …，βN為回歸參數(shù)；N 為模型階次；M為樣本的個數(shù)。模型的殘差為

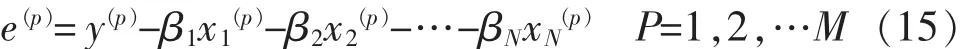
假設(shè)：

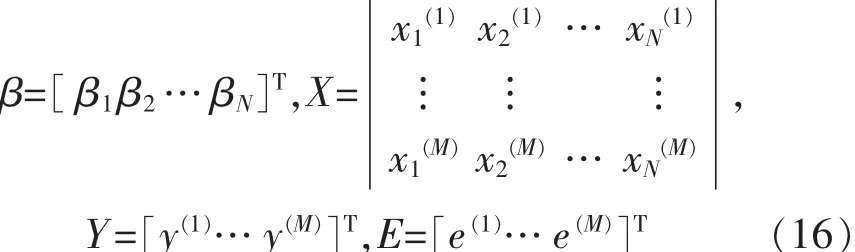
最小二乘法估計就是尋找參數(shù)估計值 β1′，β2′，…，βN′，使誤差平方和最小，即按如下目標(biāo)函數(shù)進(jìn)行優(yōu)化：

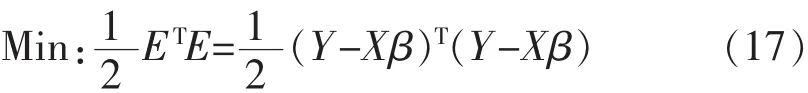
對上式求導(dǎo)，得到最小二乘估計的解為

3.3 負(fù)荷溫度模型參數(shù)求取

經(jīng)過平穩(wěn)化后的負(fù)荷溫度時間序列，其相關(guān)圖如圖3所示，通過觀察其相關(guān)圖的拖尾性可以大致確定該序列的ARMAX結(jié)構(gòu)，其自回歸及滑動平均的階次為3和5，初步考慮可以采用ARMAX（3，2，5）結(jié)構(gòu)。

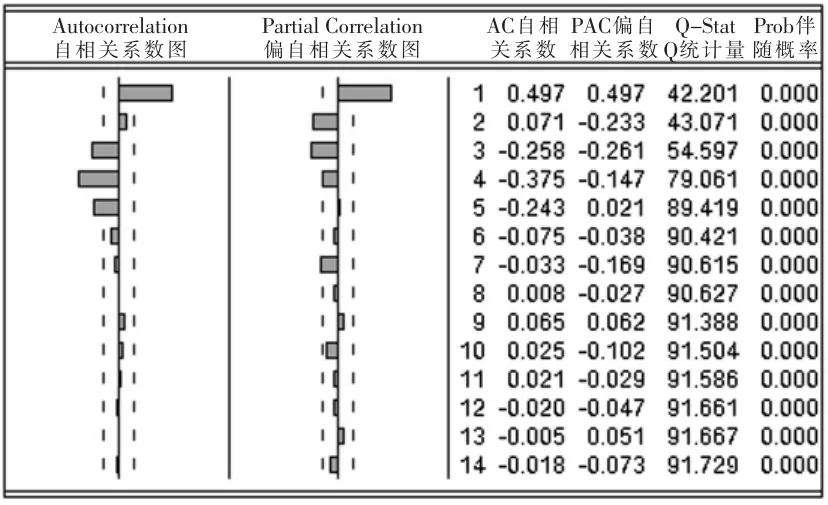
圖3 供水溫度時間序列相關(guān)圖Fig.3 Correlogram of supply water temperature series

根據(jù)以上確定的模型階次，獲得了一系列的模型結(jié)構(gòu)。此時，需要根據(jù)AIC和SC參數(shù)最小的原則進(jìn)行最優(yōu)模型選擇[10]。經(jīng)過結(jié)果比較，最終選擇的模型為 ARMAX（3，2，4）。借助于計算機(jī)仿真軟件進(jìn)行參數(shù)辨識和最優(yōu)選擇，得到的最終模型如下：

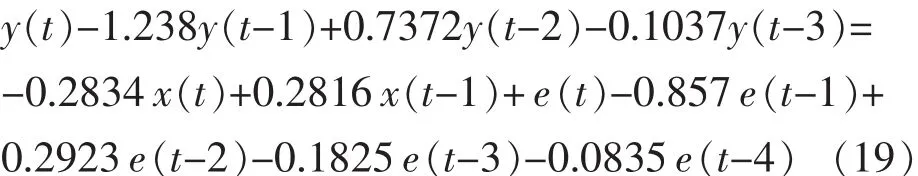
4 模型檢驗和熱負(fù)荷預(yù)測

在對數(shù)據(jù)進(jìn)行建模過程中，要檢驗?zāi)Ｐ偷倪m用性，模型適用才能輸出模型。模型檢驗的實質(zhì)是對模型殘差序列進(jìn)行白噪聲檢驗[11-12]。若殘差序列非白噪聲，說明一些重要信息沒被提取，應(yīng)重新設(shè)定模型。對殘差進(jìn)行純隨機(jī)性檢驗。對殘差序列進(jìn)行相關(guān)性分析，輸入滯后階數(shù)為14，得到如圖4所示的相關(guān)圖。

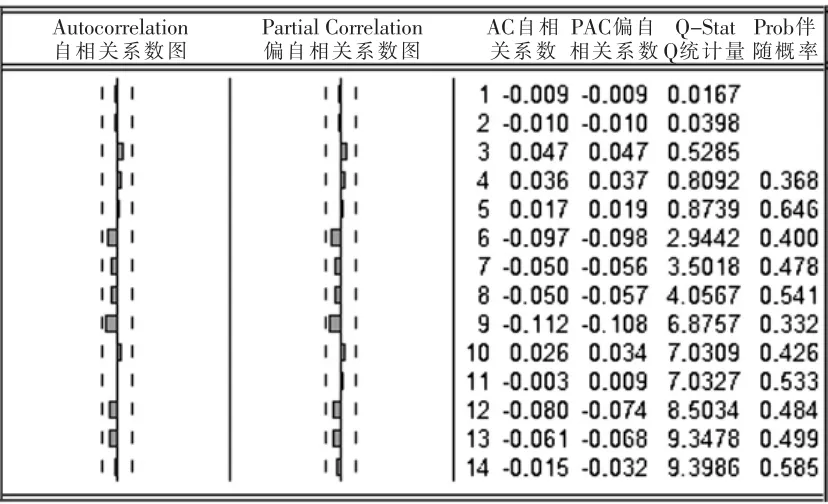
圖4 殘差序列相關(guān)圖Fig.4 Correlogram of error series

通過相關(guān)圖的分析不難看出，殘差為白噪聲，表示擬合模型有效。模型的擬合結(jié)果如圖5所示。該圖中的下半部分的空心圓連接線代表誤差曲線，上半部分的粗實線代表實際的供水溫度（經(jīng)過一階差分后的序列），叉號連接線代表利用模型獲得的擬合值。

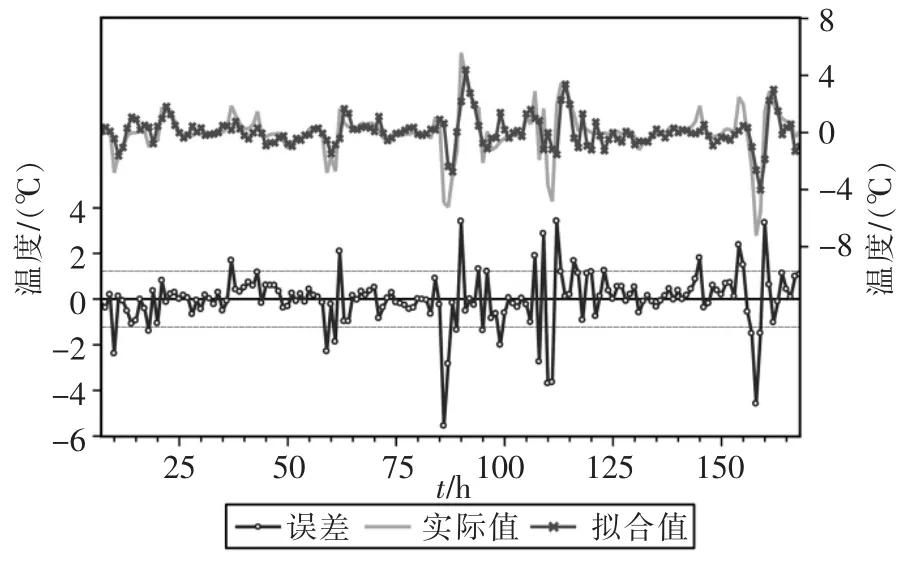
圖 5 ARMAX（3，2，4）模型擬合圖Fig.5 Fitting figure of ARMAX（3，2，4）

之后，按照已經(jīng)建立的熱負(fù)荷預(yù)測模型（19），對未來時刻的供水溫度進(jìn)行預(yù)測。為了驗證模型的有效性，首先需要給出模型準(zhǔn)確度評價標(biāo)準(zhǔn)。由于預(yù)測值和真實值之間的誤差有正有負(fù)，因此采用MPAE（平均絕對百分比誤差）來進(jìn)行總體準(zhǔn)確度評價。MPAE定義為

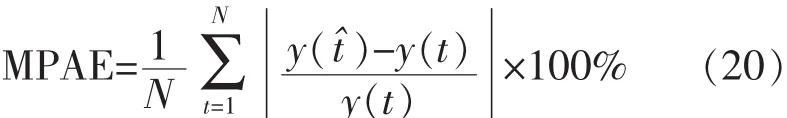
還有一個評價標(biāo)準(zhǔn)是最大誤差百分比，是指在一定時間段內(nèi)所有時刻的誤差百分比中的最大值，記為MPE（最大百分比誤差）。

對供水溫度進(jìn)行預(yù)測，并與實際運(yùn)行值進(jìn)行對比，得出預(yù)測模型的準(zhǔn)確度。由于時間序列模型采用遞推的方式進(jìn)行，易得到下一小時的供水溫度預(yù)測值，其他時刻負(fù)荷預(yù)測計算方法與此相似。最終得到了未來24 h供水溫度預(yù)測表如表1所示。

經(jīng)過計算，該模型的MPAE的值為2.6657%，MPE的值為4.9753%。通過與預(yù)期誤差百分比相比較，即可對模型的預(yù)測精度進(jìn)行評價。經(jīng)過逐步遞推，得到了未來72h的MPAE和MPE的值，如表2所示。

可見，當(dāng)時間延長后，模型的準(zhǔn)確度開始下降。平均誤差百分比開始增大，并且最大誤差百分比呈現(xiàn)很高的態(tài)勢。因此，在做實際預(yù)測時必須結(jié)合容差考察模型的適用周期，在適用周期以外需要對模型參數(shù)重新計算和調(diào)整，使其滿足精度要求。

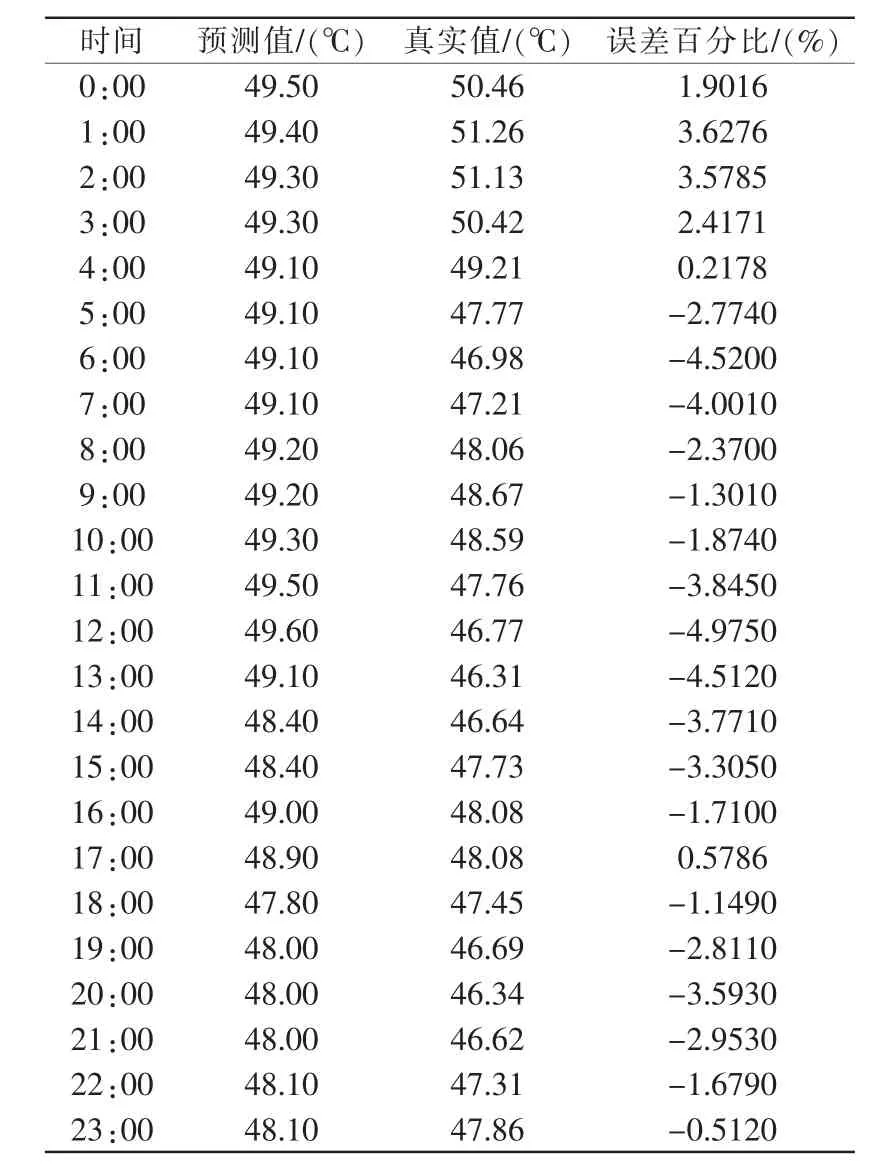
表1 24 h預(yù)測數(shù)值及誤差大小Tab.1 24 hours predicted value and corresponding error

表2 未來72 h內(nèi)的誤差百分比Tab.2 Percentage error of the next 72 hours

5 結(jié)語

通過驗證發(fā)現(xiàn)，利用ARMAX模型進(jìn)行集中供熱系統(tǒng)熱負(fù)荷預(yù)測時，計算簡單并且所需數(shù)據(jù)少，在一定的誤差范圍內(nèi)是很有效的。短期預(yù)測準(zhǔn)確度很高，但在進(jìn)行長期預(yù)測時精度下降。通過對供熱負(fù)荷進(jìn)行分析建模實現(xiàn)準(zhǔn)確預(yù)測，為負(fù)荷分配及優(yōu)化調(diào)度提供數(shù)據(jù)支持，對于能源的合理規(guī)劃和高效利用都具有重要意義。

[1] 石兆玉.供熱系統(tǒng)運(yùn)行調(diào)節(jié)與控制[M].北京：清華大學(xué)出版社，1994：135-160.

[2] 張艷.基于模糊神經(jīng)網(wǎng)絡(luò)的集中供熱負(fù)荷預(yù)測[D].阜新：遼寧工程技術(shù)大學(xué)，2009，12：1-5.

[3] 朱學(xué)莉，齊維貴，陸亞俊.建筑供熱負(fù)荷預(yù)報與預(yù)測控制策略研究[J].控制科學(xué)與決策，2002，11（17）：703-706.

[4] 袁曉輝，王乘，張傳勇.電力系統(tǒng)短期負(fù)荷預(yù)測方法的進(jìn)展[J].電氣自動化，2004，26（6）：13-16.

[5] 李晉，秦琳琳，岳大志，等.試驗溫室溫度系統(tǒng)建模與仿真[J].系統(tǒng)仿真學(xué)報，2008，20（7）：1869-1875.

[6] 王東亞.基于自適應(yīng)遺傳人工神經(jīng)網(wǎng)絡(luò)的集中供熱負(fù)荷預(yù)測和控制研究[D].阜新：遼寧工程技術(shù)大學(xué)，2005，11：4-6.

[7] 葉瑰昀，羅耀華，劉勇，等.基于ARMA模型的電力系統(tǒng)負(fù)荷預(yù)測方法研究[J].信息技術(shù)，2002（6）：74-76.

[8] 張曉峒.計量經(jīng)濟(jì)學(xué)基礎(chǔ)[M].天津：南開大學(xué)出版社，2007：282-335.

[9] 韓路躍，杜行檢.基于Matlab的時間序列建模與預(yù)測[J].計算機(jī)仿真，2005，22（4）：105-107.

[10]黨紅剛，馬亮亮.基于ARIMAX模型的海西州地區(qū)高血壓月發(fā)病率預(yù)測[J].中國老年學(xué)雜志，2011，11（31）：4428-4430.

[11]劉嚴(yán)崴.基于神經(jīng)網(wǎng)絡(luò)的供熱系統(tǒng)負(fù)荷預(yù)測[D].天津：天津大學(xué)，2009，08：33-34.

[12]萬志宏.基于時間序列的電力系統(tǒng)短期負(fù)荷預(yù)測研究[D].廣州：華南理工大學(xué)，2012，04：20-30. ■