電能計量設備自動檢定流水線調度優化研究
方彥軍,唐 猛
(武漢大學 自動化系,武漢 430072)
隨著“集中檢驗、統一配送”的電能計量裝置管理模式的推廣,近年來,多個省級電力公司都相繼建立了各自的省級計量檢定中心。同時,電力需求側管理現代化發展水平的不斷提高,也對電能計量裝置的管理、檢定的效率提出了更高要求。電能計量設備自動檢定流水線是一種現代化電能表檢定裝置,能夠實現電能表檢定過程的全程自動化。因此,如何提高自動檢定流水線的檢定效率,已成為目前各省級計量檢定中心亟待解決的難題。
為提高檢定效率,需將不同批次、相同電壓等級的計量裝置放在一條流水線上進行檢定,這就對檢定流水線的調度提出了更高要求。對于該類混合流水線調度問題HFSP(hybrid flow-shop scheduling problem),文獻[1-6]均進行了深入研究。本文針對其特點,設計了一種包含檢定排序和設備選擇信息的編碼和解碼方法,將遺傳算法得到的精英解作為禁忌算法的初始解,并運用“高”鄰域候選集策略,來提高遺傳禁忌混合算法的尋優能力。
1 自動檢定流水線調度問題數學模型
1.1 問題描述
為了提高智能計量設備自動檢定流水線的效率,生產調度中心會依據用戶需求、智能立庫存儲量及檢定周期等因素,將不同批次的同類型計量器具(單相電能表)或相同電壓等級的不同類型器具(單相電能表和終端)放在一條流水線上進行檢定。同時,在至少一個檢定環節(如:多功能檢定環節)中存在多條獨立的并行檢定單元,且每個檢定單元含有多個檢定工位,可實現多批次、多計量設備的同時檢測。因此需要將待檢器具進行分批組處理,每個批組的大小也可不同。
根據上述分析,本文將此類自動檢定流水線定義為帶批組的并行混合流水線[17-19]。帶批組并行混合流水線調度問題可描述為:n個計量器具分為B個批組在流水線上進行S個環節的檢測,各環節至少有一臺檢定設備且至少有一個環節存在并行的檢定設備,同一環節中各檢定設備檢測同一計量器具的檢測時間均相同[11],每個批組在同一環節的檢測時間不完全相同,在每一環節各待檢器具均要完成一道工序,但各待檢器具的每道工序可在相應環節中的任意并行檢定設備上檢定,已知待檢器具各道工序的檢定時間,要求確定所有待檢批組的排序以及每一環節中并行檢定設備的任務分配情況,從而使得總檢定完成時間最小,即最小化最大檢定時間,圖1為自動檢定流水線流程圖。
1.2 數學模型
令 Ji為待檢器具的編號,i={1,2,……,n},其中n為待檢器具總數;bL為第L批組中的待檢器具數量,L={1,2,……,B},其中 B 為待檢器具的批組總表示批組 L 中的第 f個待檢器具,f={1,2,……,bL},aL,f與 Ji是一一對應的;md為檢定環節 d 中的并行設備數,d={1,2,……,S},其中 S 為環節總數;td,L為批組 L 在環節 d 的檢測時間;Sd,L為批組L在環節d的檢測開始時間;ed,L為批組L在環節d的檢測結束時間;CL為批組L的檢定完成時間;Cmax=max{C1,C2,……,CB}為所有批組檢定完成的最大時間;則具體的數學模型為

其中:式(1)為調度優化指標;式(2)表示每個優先級位置只能對應一個批組;式(3)表示每個批組只能占有一個優先級位置;式(4)表示每個環節每個批組只能在一臺檢定設備上進行檢測;式(5)表示同一環節檢測開始時間與完成時間的關系;式(6)表示同一批組在不同環節間的先后約束關系;式(9)表示同一環節排位越前的批組開始檢測的時間越早;式(10)表示同一環節分配在同一設備上的不同批組,優先級靠前的批組檢測完后才允許后面的批組進行檢測。
2 基于GATS算法的自動檢定流水線調度
2.1 遺傳禁忌混合算法
遺傳算法是通過將具體問題的求解抽象成生物“染色體”種群的一代代進化,包括選擇、交叉和變異等操作,最終找到“最適應環境”的最優個體,從而完成對問題最優解的自適應搜索。該算法的大范圍搜索能力較強,但局部搜索能力較差[13]。
禁忌搜索TS(tabu search)算法具有靈活的記憶功能,在搜索過程中可以接受劣解,從而跳出局部最優解,具有很強的局部搜索能力,但該算法對于初始解的依賴性較強[14]。將遺傳算法與具有記憶功能和較強“爬山”能力的禁忌算法混合使用,一方面能夠提高禁忌算法搜索效率,同時又能克服GA爬坡能力弱的缺點[7]。為了結合兩種算法的各自優勢,本文采用一種改進的遺傳禁忌算法,并運用多精英策略[8-9],即選取適應度排位靠前的精英解與非精英解進行交叉操作。對遺傳操作得到的解集進行重新排位,選取適應度排位靠前的精英解作為禁忌操作的初始解,并利用禁忌搜索中得到的最優解對初始解進行替代更新,直至滿足一定條件跳出算法得到最優解。算法流程如圖2所示。
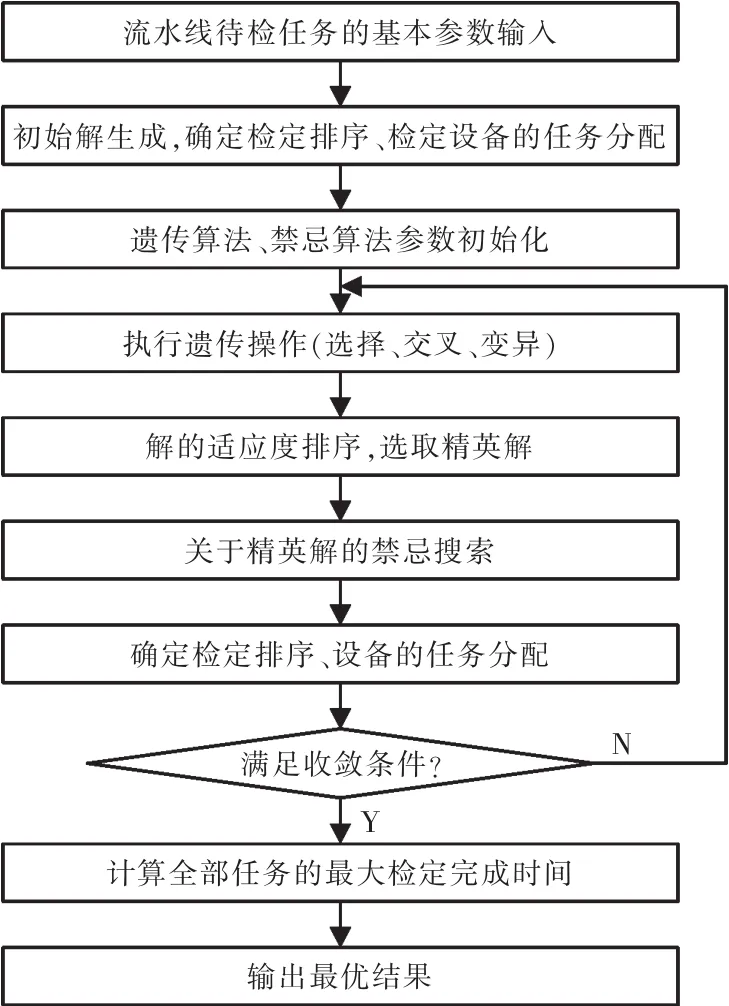
圖2 改進的遺傳-禁忌混合算法流程Fig.2 Procedure of improved GATS algorithm
2.2 編碼與解碼
待檢器具的批組總數為B,則令染色體長度為B,編碼矩陣 AS*B構成一個染色體,見式(11),表示一共B個批組需要經過S個檢定階段,至少一個階段存在md臺并行檢定設備,每個染色體與解集是一一對應的。 其中矩陣中的元素 ad,L為區間(1,1+md)的一個隨機實數,表示批組L的第d個檢定階段在第 Int(ad,L)臺并行設備上進行檢定,染色體中包含了各個批組在不同檢定階段的檢定順序及設備選擇信息。例如,個體[a1,1,a1,2,a1,3……]=[1.1,1.3,1.2……],1.3表示批組2的第一個階段在設備1上進行檢定,小數位“3”表示在同一階段選擇同一設備的批組檢定順序,所有待檢批組的序號在個體中的位置表示各批組的檢定排序,因此基因在染色體中的相對位置直接反映出各批組的檢定順序。根據1.2節所述的約束條件確定同時包含各批組檢定排序和各階段并行檢定設備的任務分配策略即稱為解碼。

對于確定待檢批組的檢定排序,即為確定不同批組在相同階段的檢定開始時間排序。本文采用以下策略:按照先到先服務FCFS(first come first service)的方式確定檢定排序,即前階段先完成的批組先進行下一階段的檢定。若多個批組在該階段并行設備上的檢定完成時間相同,則仍然按照前一階段的排序進行后續階段的檢定。對于并行檢定設備的分配問題,采用最先閑置機器原則[4]:
1)根據各批組在前一階段的檢定順序,依次計算每個批組在下一階段第k臺并行檢定設備上的最早允許檢定時間 Pd,L,k=max(Cd-1,L;rk),其中 rk為并行設備k的最先空閑時間。
2)計算下一階段各并行設備的優先系數aL,k=max(Cd-1,L;rk)+td,L,選擇優先系數值最小的設備作為其在該階段的檢定設備,并更新批組L在階段d的檢定完成時間Cd,L和設備k的最先空閑時間rk。
2.3 種群初始化
為了使初始解保持一定的分散性,本文采用隨機方法產生初始化解 Si,i=1,2,…Psize。
2.4 適應度函數與選擇
本文的優化目標為所有待檢批組的最大完成時間,為了避免算法出現早熟和隨機漫游現象,采用乘冪變換對目標函數進行適度縮小,則適應度函數為
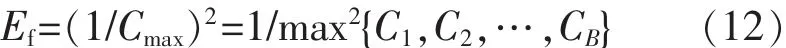
式中,Cmax(Q)為第Q個染色體所代表的一個調度方案的最大檢定周期。選取每代中適應度值排位在前ω的精英解采用最佳個體保存法,即直接復制到下一代,對其余解按照輪盤賭法進行選擇。
2.5 交叉和變異
將適應度值排在前列的精英解與非精英解進行隨機的自適應單點交叉操作[9],并驗證交叉后得到的解是否滿足所有約束條件。具體算法如下:
1)選取一個隨機概率大于預設交叉概率的非精英解與一隨機精英解進行交叉操作,并對交叉后的解進行有效性驗證,包括驗證其是否滿足上述所有約束條件;
2)將交叉后的子代與非精英父代的適應度值進行對比,若子代的適應度值優于父代,則子代個體自動取代非精英父代個體進入下一代種群;否則仍然保留父代個體。
本文采用一種混合變異算子[10],若當前種群的目標函數最大值與最小值之差小于某一正數時,采用高斯變異,否則采用邊界變異。因此,在進化初期采用邊界變異,即首先選取不同類型的批組所在的基因位作為變異點,然后用兩者對應的邊界基因之一替代原有基因值;后期主要進行高斯變異來提升算法對重點區域的搜索能力。
2.6 禁忌搜索
2.6.1 鄰域結構及候選集
本文首先采用交換鄰域結構:任意選擇同一檢定設備上的兩個批組,交換其檢定順序。其次,采用“高”候選集策略產生候選集[15],即:將總檢定完成時間最大的并行機上任意批組插入到總檢定時間最小的并行機上任一批組前。
2.6.2 禁忌表的設計
禁忌表采用先進先出的隊列來實現。在禁忌搜索過程中,會出現當前解的領域全部被禁忌,或是某一解被禁忌后當前最優值將下降的情況,為了避免搜索算法丟失優化狀態實現全局最優,本文基于特赦規則:根據解的適應度值,若出現某個候選解的適應度值優于當前最優解時,雖然從當前最優解到該解的變化被禁忌,但可以解禁該候選解作為當前最優解[12]。
2.6.3 關于精英解的禁忌算法
禁忌算法的終止規則選用目標控制原則:當前已存在的最優解的適應度值連續nt次大于之后搜索到的解適應度值,則停止搜索[16]。禁忌搜索算法流程如圖3所示。
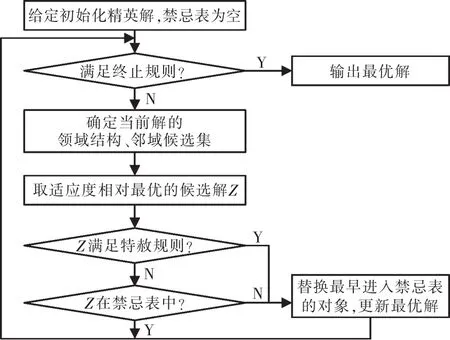
圖3 TS算法流程Fig.3 Flow chart of TS algorithm
3 實例
某省級電能計量設備自動檢定中心對一批含有9個不同批組的電能計量設備進行檢定。每個批組都要經過外觀、耐壓檢測環節,多功能檢測環節,分揀、封印及自動貼標簽環節等3大環節共6個單元的檢定。其中在多功能檢測環節有3組并行且獨立的U型檢測工位,每個工位含有60個表位可同時進行檢測,即 BL≤60,B∈(0,6),但是不同批組在每個環節的檢定時間不盡相同,具體檢定時間如表1所示。
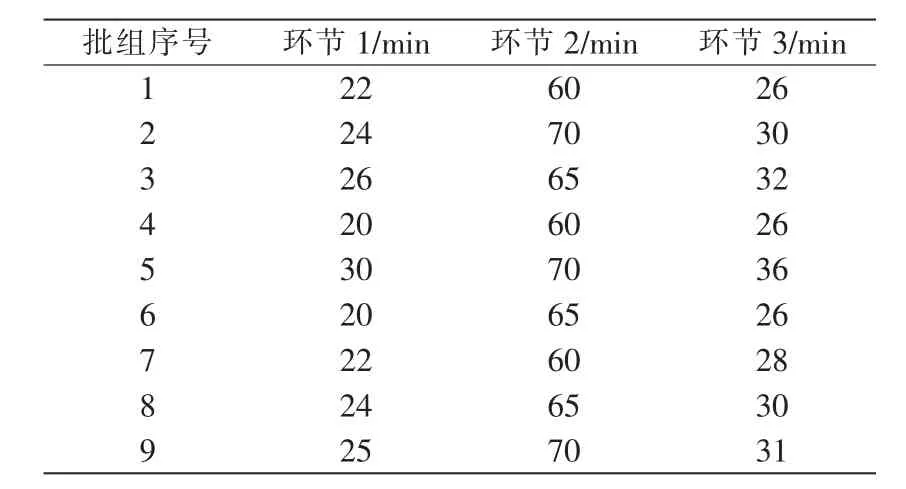
表1 檢定時間Tab.1 Verification time of the instance
運用Matlab編程來實現本文算法,混合算法參數設置如下:遺傳種群數量為80,交叉概率為0.9,變異概率為0.1,精英保留率取ω=20%,遺傳算法最大進化代數為200,禁忌鄰域解個數為10,候選解的個數為8,禁忌表長度為8,禁忌終止條件為連續nt=8次無法找到適應度值更優的解。
為更好地驗證該混合算法具有收斂快、優化率高的特性,以實例為背景,將本文提出的IGATS與ABC[1]、TS[4]、PSO[6]進行比較。 表 2 為每種算法獲得最好解的10次獨立運行結果的平均值。
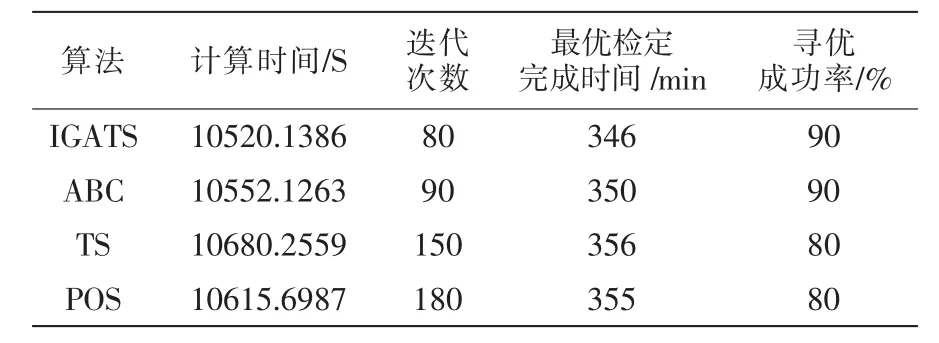
表2 實例的4種優化算法比較Tab.2 Result comparision of four optimization algorithms under the instance
從表2中可看出,本文提出的IGATS算法經過大概80次就趨于收斂,與其它3種優化算法相比,收斂速度較快,計算時間較短,且最優檢定完成時間為346 min,因此能夠尋到另外3種算法找不到的最優解,四種算法在尋優成功率方面的表現相當。綜上所述,該遺傳禁忌算法的搜索空間能力較強,并具有快速求出最好解的特性,綜合性能優于其它3種算法,能夠為檢定流水線的優化調度提供更多的理論依據。IGATS算法的最優解甘特圖如圖4所示。其中:橫坐標為各批組在該階段所需時間;縱坐標為批組在該階段所選擇的機器編號,如:機器2對應的 “1-2”表示批組1的第2個階段在設備2上進行檢定,方格長度代表所需時間的長短。
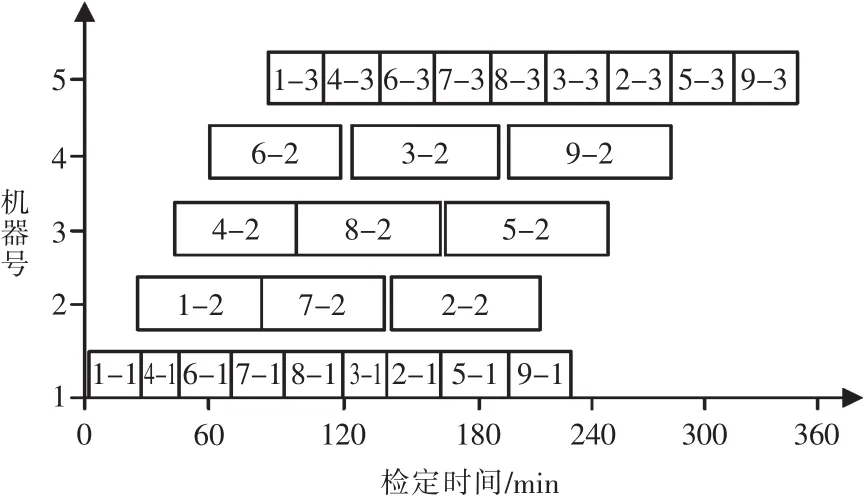
圖4 IGATS算法的最優解甘特圖Fig.4 Gantt chat of the optimal solution
4 結語
針對電能計量設備自動檢定流水線調度問題,本文提出一種有效的遺傳禁忌混合算法:設計了一種包含檢定排序和設備選擇信息的編碼和解碼方法,將遺傳算法得到的精英解作為禁忌算法的初始解,并運用“高”鄰域候選集策略,來提高混合算法的尋優能力。以某省級檢定中心自動檢定流水線為背景,將該算法與另外3種優化算法進行比較,表明該算法收斂速度更快、優化率更高,得到的解最優,具有較強的有效性和魯棒性。
[1] 王凌,周剛,許曄,等.求解不相關并行混合流水線調度問題的人工蜂群算法[J].控制理論與應用,2012,29(12):1551-1557.
[2] PAN Q K,TASGETIREN M F,SUGANTHAN P N,et al.A discrete artificial bee colony algorithm for the lot-streaming flow shop scheduling problem[J].Information Sciences,2010,181(12):2455-2468.
[3] 王圣堯,王凌,許曄.求解相同并行機混合流水線車間調度問題的分布估計算法[J].計算機集成制造系統,2013,12(6):51-15.
[4] WANG X,TANG L.A tabu search heuristic for the hybrid flow-shop scheduling with finite intermediate buffers[J].Computers&Operations Research,2008,36(3):907-918.
[5]ALAYKYRAN K,ENGIN O,DOYEN A.Using ant colony optimization to solve hybrid flow shop scheduling problem[J].InternationalJournalofAdvanced Manufacturing Tech-nology,2007,35(5/6):541-550.
[6] TSENG C T,LIAO C J.A particle swarm optimization algorithm for hybrid flow-shop scheduling with multiprocess-or tasks[J].International Journal of Production Research,2008,46(17):4655-4670.
[7] 姚靜,方彥軍,陳廣.遺傳和禁忌混合算法在機組負荷分配中的應用[J].中國電機工程學報,2010,30(26):95-99.
[8] 朱燦,梁昔明.一種多精英保存策略的遺傳算法[J].計算機應用,2008,28(4):929-931.
[9] 劉愛軍,楊育,邢青松,等.復雜制造環境下的改進非支配排序遺傳算法[J].計算機集成制造系統,2012,18(11):446-458.
[10]呂瀟,孫躍.復合諧振感應電能傳輸系統分析及參數優化[J].電力系統自動化,2013,37(4):119-124.
[11]ZHANG C S,OUYANG D T,NING J X.An artificial bee colony approach for clustering[J].Expen Systems with Applications,2010,37(7):4761-4767.
[12]陳鐵梅,羅家祥.帶擾動和變異因子的改進禁忌搜索算法求解貼片機過程優化[J].控制與決策,2013,28(3):363-368.
[13]ALFIERI A.Workload simulation and optimization in multicriteria hybrid flow-shop scheduling:A case study[J].International of Production Research,2009,47(18):29-45.
[14]ORTMANN M C,VIGNIER A,DARDILHAC D,et al.Branch and bound crossed with GA to solve hybrid flow-shops[J].Europe Journal of Operational Research,1998,107(2):389-400.
[15]Chiang C L.Genetic algorithms for power economic[J].IET on Generation Transmission and Distribution,2007,11(2):261-269.
[16]蘇凱,劉吉臻,牛玉廣.考慮直吹式鋼球磨電耗的廠級負荷優化分配[J].中國電機工程學報,2012,32(2):24-30.
[17]XU Y,WANG L.Differential evolution algorithm for hybrid flow-shop scheduling problem[J].Journal of Systems Engineering and Electronics,2011,22(5):794-798.
[18]王凌,周剛,許燁,等.混合流水線調度研究進展[J].化工自動化及儀表,2011,38(1):1-8.
[19]王凌.車間調度及其遺傳算法[M].北京:清華大學出版社,2003.■

